第250回 シーズン25 エピソード10

「考える」ことの意味（後編）

リビングにて

ノナ「点をぜんぶいっぺんに上げます $\NONAEX$ 　ぜんぶの点を《$1$ だけ上げる》という意味 $\NONAQ$」

僕「そうだね！　その通り！　ノナちゃんが言ってる《点》というのは、直線 $y = x$ 上の点のことだね？」

ノナ「そう $\NONAEX$ 　ぜんぶジャンプ $\NONAEX$」

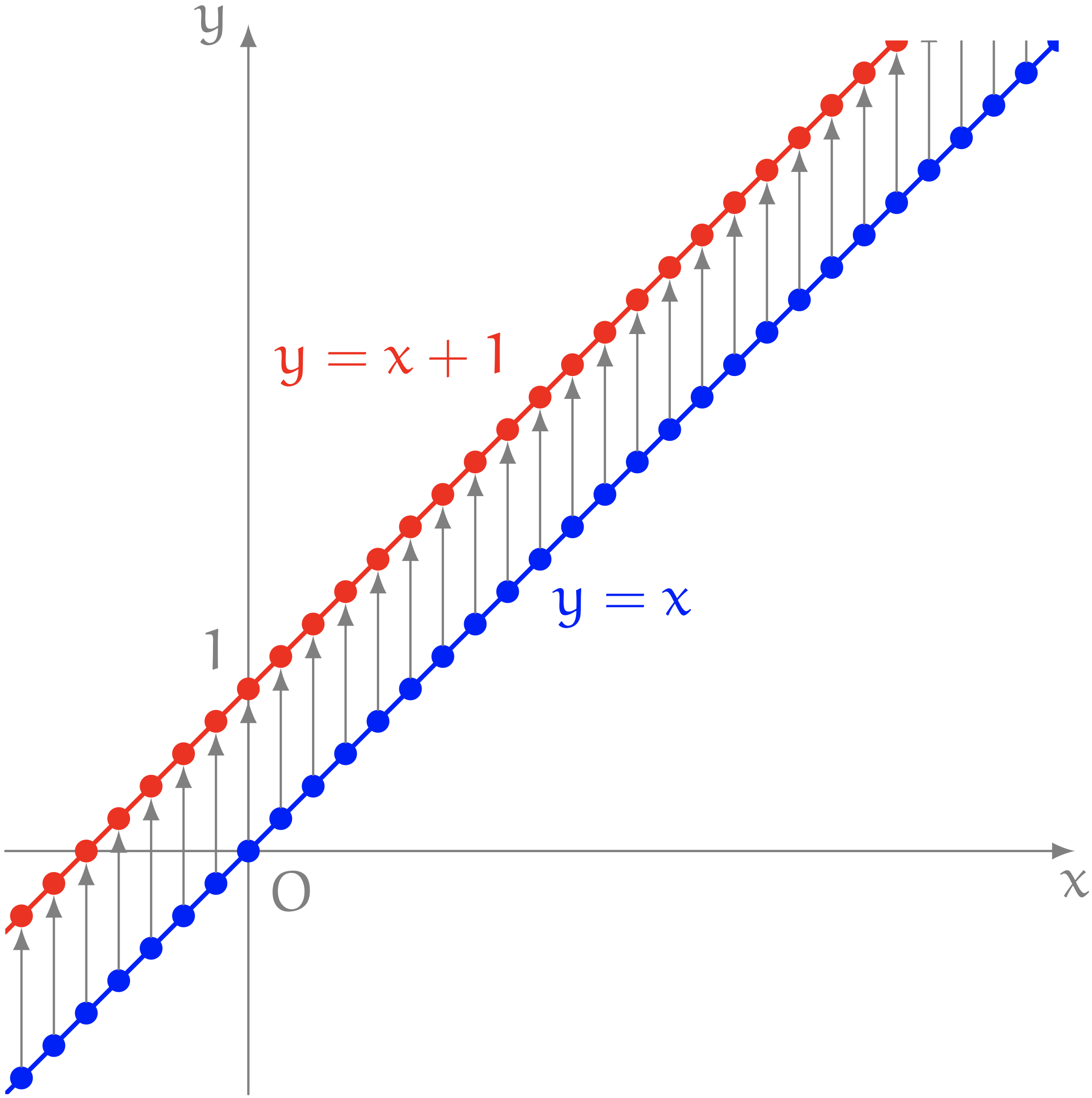
僕「これで完全に準備が整ったよ」

• 直線 $y = x$ というのは、 $y = x$ を満たす点がすべて集まっている図形。
• 直線 $y = x + 1$ というのは、 $y = x + 1$ を満たす点がすべて集まっている図形。
• 図形を《$1$ だけ上げる》というのは、その図形のすべての点の $y$ 座標を $1$ 増やして得られる図形を求めること。

僕「あとは、直線 $y = x$ のすべての点について、 $1$ だけ上げた図形が、直線 $y = x + 1$ 上にあることを確かめればいいんだ」

ユーリ「ほほー？」

ノナ「ほほう $\NONAQ$」

僕「ノナちゃんは、どうしたらいいと思う？」

ノナ「わからない……わかりません $\NONAX$」

僕「《生徒役のノナちゃん》が『わかりません』と言ってますが、 《先生役のノナちゃん》にその気持ちを解説してもらいたいなあ」

ノナ「何を聞かれてるのかわからない……みたい $\NONA$」

僕「ああ、なるほど。 僕の質問が雑だったからね。 じゃあ、きちんと質問するよ」

ユーリ「$y = x$ を $1$ だけ上に動かしたら $y = x + 1$ なんて、当たり前じゃん」

ノナ「ユーちゃんは、頭いいから $\NONA$」

僕「いやいや、ノナちゃん。頭の良し悪しの話じゃないよ。 数学を考えよう。 『これを確かめるためには、何をいえばいいでしょうか』」

ノナ「わからない……わかりません $\NONAX$」

僕「《先生役のノナちゃん》にもう一度お尋ねしますが……」

ノナ「何を聞かれてるのかはわかった……みたい $\NONA$」

僕「それはよかった」

ノナ「何を答えたらいいのかはわからない……わかりません $\NONAX$」

僕「じゃあね、『直線 $y = x$ 上にある点はどれでも、 $1$ だけ上に動かすと、直線 $y = x + 1$ 上にある』と言われたら、 ノナちゃんは納得できるかなあ」

僕「なるほど。ノナちゃんは納得できる。 だったら、ノナちゃんのその《納得》を言葉にすることはできるかな？」

ノナ「だって……この通り $\NONA$」

僕「そうだね。 この図には、直線 $y = x$ の点を $1$ だけ上に動かしているようすが描いてある。 それが、はっきりと見える。だからノナちゃんは、納得できる」

僕「見えている通りなのに、どうしてそんなに当たり前のことを聞くんだろう。 当たり前のことだから、何と答えていいかわからない……のかな」

ユーリ「実際、当たり前だよね！」

僕「図に描くと確かにわかりやすいけれど、見えている通り……というのは、数学では確かめたことにはならないんだ。 だって、ほら、ノナちゃんも知っているように、座標平面というのは、ここに見えている範囲だけじゃないよね」

ノナ「《無限のキャンバス》$\NONAEX$」

僕「そうそう。座標平面というのは、無限に広がっているキャンバスのようなもの。 この紙に描いたものは、ほんの一部分だけなんだ。しかも、数学の《点》では大きさを考えない。 この紙に描いた丸い点は、僕たちが考えるための手がかりに過ぎないんだよ」

ノナ「$\NONA$」

僕「だから『直線 $y = x$ 上にある点はどれでも、 $1$ だけ上に動かすと、直線 $y = x + 1$ 上にある』 ということを数学的に確かめるためには……《無限を味方につける》必要がある」

ユーリ「お兄ちゃんのポエムが始まったぞ」

ノナ「無限 $\NONA$」

僕「図は目に見えてわかりやすいけど、限りがある。 僕たちは、図の助けを借りつつ、数式を使って確かめるんだ」

ユーリ「まわりくどーい！　結局、どーすんの？　早く早く早く！」

僕「僕たちはいま、直線のような図形を《点の集まり》として考えている。 だから、点をたとえば、 $$ (x, y) = (p, q) $$ のように表して考えればいいんだ。つまり、 $x$ 座標が $p$ という値で、 $y$ 座標が $q$ という値になっている点を考えてみよう」

ノナ「$p$$\NONAQ $」

僕「$p$ と $q$ のように文字を使う。それを使って $(p,q)$ のように点を表すのは、 《無限を味方につける》ための一つの方法なんだよ、ノナちゃん」

ノナ「なんで……どうしてですか $\NONAQ$」

僕「うん。 $1$ や $2$ のように具体的な数を使って考えた方がわかりやすいけど、 それだと、一つの点しか考えていないことになるよね。 でも、僕たちはいま、無数の点について一般的な主張をしたい。 だから、文字を使うんだ」

ユーリ「お兄ちゃんがよくやるやつだ！　《文字の導入による一般化》でしょ？」

ノナ「もじの $\NONA$」

ユーリ「《文字の導入による一般化》」

ノナ「もじのどうにゅうによる……いっぱんか $\NONA$」

僕「そうだね。ユーリのいう通り。 $1$ や $2$ のような具体的で特別な数を使うんじゃなくて、 $p$ と $q$ という文字を使って一般的に考えようということ」

ノナ「大事なこと $\NONAQ$」

僕「そうだよ。一般的に考えるのはとても大事なこと。 なぜかというと、さっきノナちゃんが考えていたことを確かめるため」

ノナ「$\NONAQ$」

僕「ノナちゃんは《直線上のぜんぶの点を $1$ だけ上に動かす》ことを想像したよね。 紙の上でも《見た》けど、心の中でも《見た》はずだよ。直線を動かすようすを」

ノナ「見た……見ました $\NONA$」

僕「具体的な数で理解するのはとてもいい。《例示は理解の試金石》だから。 でも、いったん理解したら、今度は具体的な数を文字にして一般的に考えようとしてみる」

ユーリ「お兄ちゃん、それ大得意だよね」

ノナ「もじのどうにゅうによるいっぱんか $\NONA$」

僕「$(p, q)$ のように文字を使えば、たった一つの点だけじゃなくて、 無数にある点のことを一度に表せる。 そうすれば、直線上の《ぜんぶの点》をまとめて考えることもできるんだ！」

ノナ「無限のキャンバス $\NONA$」

僕「ああそれから、ついでに言うと、 こんなふうに自分が覚えたことを当てはめるのは大事だよ。つまり……」

• 《例示は理解の試金石》という言葉を覚えたら、抽象的な話を聞いたときに「よし、具体例を作ってみよう」と考えること。
• 《文字の導入による一般化》という言葉を覚えたら、具体的な数を見たときに「よし、この数を文字に変えて、一般化してみよう」と考えること。

ユーリ「なーるほど。当てはめること？」

僕「そうだね、自分が覚えたことを当てはめてみる。 いわば《法則の適用》とでもいうこと。 そうすると世界が広がるんだ」

ユーリ「ほーそくのてきよー」

ノナ「ほうそくの……てきよう $\NONA$」

僕「じゃあ、話を戻すよ。文字 $p, q$ を使って点 $(p, q)$ を考えて……」

ユーリ「お兄ちゃん、ちょっと待って。 もともと点は $(x,y)$ って文字を使ってたじゃん。 $x$ と $y$ ってゆー文字。何でわざわざ $p$ とか $q$ とか別の文字を使うの？」

僕「うん、 $x$ と $y$ のまま話をしてもいいし、そういうこともよくある。 でもそのときには『いま $(x,y)$ は何を表しているかな』と注意しないといけない。 話をわかりやすく……誤解なく進めるために、 $p$ と $q$ という別の文字を使おうと思ったんだよ」

ユーリ「へー。そんじゃ、話を先に進めてくれたまえ」

僕「ここまでの話、ノナちゃんは大丈夫？　何か気になることはある？」

ノナ「大丈夫……大丈夫です $\NONA$」

僕「……」

ユーリ「おにーちゃん！　どーした！」

ノナ「$\NONAQ$」

僕「うん。ノナちゃんは、気になることはない？」

ノナ「大丈夫……大丈夫です $\NONA$」

（コンコン）

僕「《生徒役のノナちゃん》は『大丈夫です』と言ってますけど……《先生役のノナちゃん》はどう思います？」

ノナ「暗記が気になってる……みたいです $\NONA$」