![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/学ぶための対話』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕は高校生。いまは土曜日。
ここは僕の部屋。
いつものように、いとこのユーリが遊びに来てる。
でも、今日はいつもと違う。
今日は《もう一人の女の子》もいっしょなのだ。
ユーリ「……そんで、このかわいい子がノナだよ。ユーリとおんなじクラス」
ノナと呼ばれたその女の子は、僕に向かって頭を下げた。
彼女はユーリよりは一回り小柄。
中学生だけど、小学生のようにも見える。
登場人物紹介(追加)
ノナ:ユーリの同級生。
僕「ノナちゃん?」
ノナ「はい $\NONA$」
ノナは、ふわふわした声で答えた。
彼女はベレー帽をかぶり、丸い眼鏡を掛けている。
幼く感じるのは、やや目尻が下がった垂れ目のせいかもしれない。
ベレー帽から顔の正面に下がったノナの髪は、ひとふさだけ銀色。それが印象的だ。
ユーリ「お兄ちゃん! ノナのこと、じろじろ見ないで!」
僕「あ、ごめん」
ユーリ「でも、ノナの銀髪(ぎんぱつ)、カッコいいっしょ? ひとふさだけの銀髪メッシュなんだよ!」
ノナ「カッコよくないよう $\NONA$」
登場人物紹介(更新)
ノナ:ユーリの同級生。
ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。
僕「それで……えっと、ユーリ? ユーリは今日、ノナちゃんと一緒に来たんだよね」
ユーリ「そーだよ」
僕「これからいったい、何が始まるんだろうか」
ノナ「ユーちゃん……何も言ってなかったの $\NONAQ$」
ユーリ「要するに、数学を教えるんだよん」
僕「数学を教えるって……誰が?」
ユーリ「お兄ちゃんが」
僕「誰に?」
ユーリ「ノナに」
ノナ「よろしくお願いします $\NONA$」
僕「そう言われても……」
ユーリ「いーの、いーの。いつもと同じでリラックスして話せばいーんだから」
僕「何だそりゃ」
ユーリ「あのね、ノナは、あんまり数学得意じゃないんだよー。だから、ていねいに教えてね」
ノナ「数学、ぜんぜんだめ $\NONAX$」
ユーリ「でも、興味はすんごくあるんだよねー」
ノナ「だって、ユーちゃんの話、おもしろいから $\NONA$」
ユーリ「えー、そっかなー」
ノナ「そうだよう……この前も $\NONA$」
ユーリとノナ、仲良し中学生女子二人の会話が始まった。
僕は、しばらく放置状態になる。
漏れ聞く会話を総合すれば、こういうことらしい。
ノナは数学があまり得意じゃない。というか苦手。
授業もよくわからないし、テストで点が取れない。
でも、ユーリがノナにおもしろい数学の話をするから、興味がある。
よく話題になる《お兄ちゃん》とやらの話を聞きたい。
(ちなみに《お兄ちゃん》というのは僕のことだ)
ということで、ユーリとノナがいっしょにやって来た……
僕「……ということか」
ユーリ「そーゆーことだ」
ノナ「よろしくお願いします $\NONA$」
僕「と言われても、何を話せばいいのかなあ。ノナちゃんは数学苦手なの?」
ノナ「はい $\NONAX$」
僕「それとも数学が嫌いなの?」
ノナ「はい $\NONAQ$」
僕「得意・不得意と、好き・嫌いは違うよね」
ノナ「よくわからない……わかりません $\NONA$」
僕「ノナちゃんは、数学の授業は好きじゃないの?」
ノナ「嫌い $\NONAX$」
僕「嫌いなんだ」
ノナ「つまらない $\NONAX$」
僕「どうして授業がつまらないか、パラフレーズ……どうしてかわかる?」
ノナ「わからないから $\NONAX$」
僕「なるほど。難しいのかなあ」
ノナ「公式、嫌い $\NONAX$」
僕「覚えるのが嫌い?」
ノナ「わけがわからないから $\NONAX$」
僕は考える。
なし崩しにノナに数学を教える流れに巻き込まれているけど、 何もないところから《数学の話》なんてできないぞ。 何かとっかかりはないかなあ……
ユーリは、僕とノナのやりとりを黙って聞いている。
僕「……ねえ、ユーリ。ユーリはたとえばどんな話をしてたの?」
ユーリ「いろんな話。ノナはリサージュ図形が好きだって言ってた。だよね?」
ノナ「好き $\NONA$」
僕「リサージュ図形……」
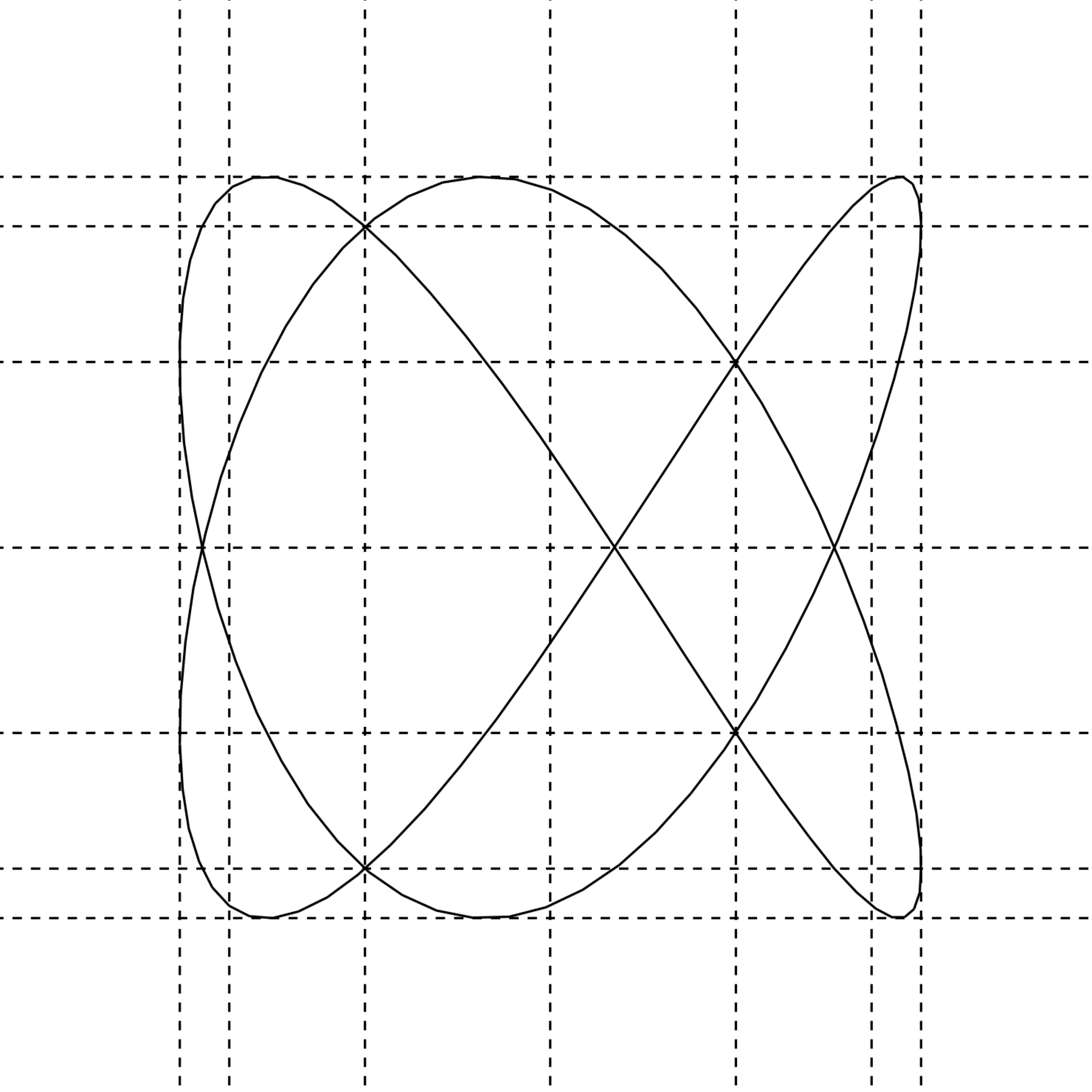
ユーリ「ユーリの活躍は『数学ガールの秘密ノート/丸い三角関数』で!」
僕「そういうの、自重……じゃ、ノナちゃんはグラフとか好きかな。 たとえば、こういうグラフはわかる?」
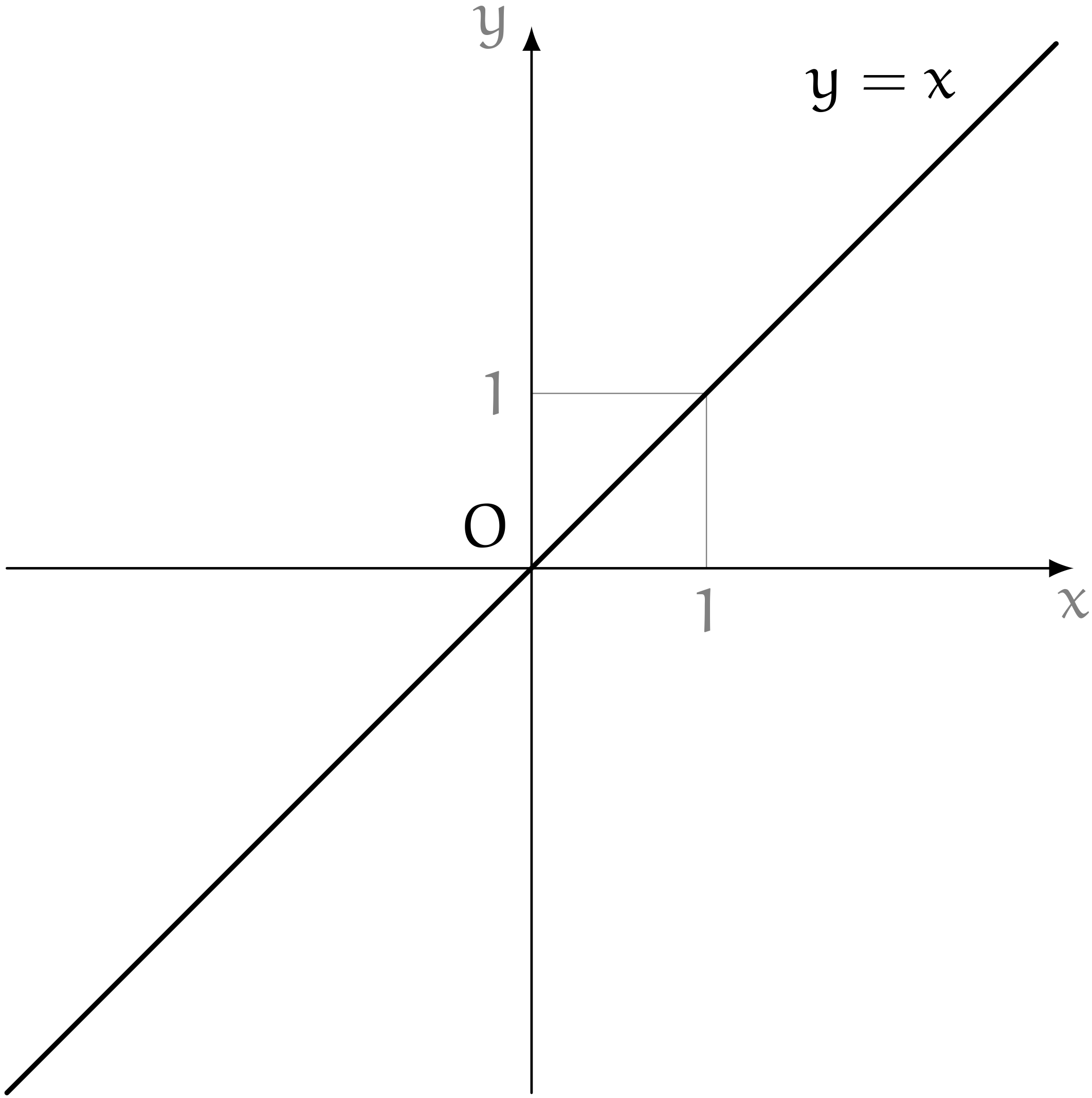
ノナ「わかる……わかります」
僕「このグラフは直線で、 $y = x$ という式で書けるんだけど、それはわかる?」
ノナ「覚えてる……覚えてます $\NONA$」
僕「覚えてるんだ」
ノナ「覚えてます $\NONA$」
僕「$y = x$ が何を表しているかはわかる?」
ノナ「$\NONAQREV$ これです」
ノナは少し変な顔をしてから、グラフを指さした。
僕「ああ、いや、そういうことを聞いてるんじゃないよ。 このグラフは直線で、 $y = x$ という式で表されているけれど、 この式自体がどういう意味なのかはわかるか、 ということを聞いてるんだ。 『覚えてる』とノナちゃんが答えたから、 『$y = x$ を覚えてるだけじゃなくて、 $y = x$ がどんな意味かを理解してるのかな』と思ったんだよ。 $y = x$ という式はどういう意味なのか、ここでは何を表しているか、 どうして $y = x$ という式がこのグラフを表していることになるのか、 そういうことはわかっているのかな、という質問なんだけど。ノナちゃん、どう?」
ノナ「……」
ノナは口を閉じ、急にけわしい表情になった。
目にちょっぴり涙が浮かんでいる。
僕はあわてた。
僕「いやいや、よくわからなかったら、わからないでもいいんだよ」
ノナ「意味がわからない $\NONAX$」
ユーリ「ちょっとちょっとちょっと、お兄ちゃん! ノナを泣かせるなよー!」
僕「そうだね。ごめん」
ユーリ「お兄ちゃんって、話が佳境に入ると急に早口になるの! ユーリは慣れてるからいーけど……」
そうだったんだ。
気を付けよう。
僕「ねえ、ノナちゃん。僕の話し方はこわい?」
ノナはポシェットから小さなハンカチを出して、軽く目に当てた。
ノナ「こわくない……こわくありません $\NONA$」
僕「よかった。話を続けても大丈夫?」
ノナ「大丈夫……でも意味がわからないと答えられない……答えられません $\NONAX$」
僕「そうだね。もちろん、意味がわからなかったら答えられない」
ユーリ「そりゃそーだ」
僕「いま僕はね、 ノナちゃんが《どんな数学をどんなふうに理解しているか》を知りたいなって思ってるんだ。 だから、いろんなことをノナちゃんに聞きたいと思っている。それはいい?」
ノナはこくんとうなずいた。
僕「もしかしたら、 ノナちゃんには意味がわからないことや、 ノナちゃんが答えられないことも聞くかもしれない。 もしも、そういうことがあったら、 遠慮しないで『意味がわからない』『何と答えていいかわからない』と言ってね」
ノナは、もう一度、こくんとうなずいた。
僕「よかった。それじゃ、話を続けるね。このグラフの式は $y = x$ と書くんだけど、この $y = x$ という式の意味を説明するよ」
ノナ「意味がある $\NONA$」
僕「うん、意味があるよ。 $y = x$ は《$y$ 座標の値と $x$ 座標の値が等しい》ということを表しているんだ。 でも、その意味をきちんと理解するには、 ひとつひとつの言葉も説明する必要がある」
ノナ「……」
僕「言葉がたくさん出てくるけど、 ひとつずつ、ちゃんと意味を説明していくから大丈夫だよ」
ノナ「意味がある $\NONA$」
僕「うん、そう。数学で出てくる言葉もグラフもぜんぶちゃんと意味があるんだよ」
ノナ「意味があるって、知らなかった $\NONA$」
僕「意味があるから、考えることができる。 いまから僕たちは、このグラフについて詳しく考えていきたいと思う。さっきと同じこのグラフだよ」

ノナが黙って銀色の前髪をいじり始めたので、僕は話を一時中断する。
そして、待つ。
彼女は、きっと何かを考えているんだ。
ノナ「……」
僕「何か気に掛かるなら、僕が話している途中でも、いつでも言っていいんだよ」
ノナ「もうある……あります $\NONA$」
僕「あるって、何があるの?」
ノナ「グラフはもう描いてある……描いてあります $\NONA$」
僕「そうだね」
ノナ「もう、グラフがここに描いてあるのに、考えるの $\NONAQ$」
僕「なるほど」
今度は僕が黙る番になった。
僕はいままで自分のことを、数学を教えるのが少しは得意だと思っていた。 いとこのユーリに教えたり、後輩のテトラちゃんに教えたりした経験から。
自分がちゃんとわかっていることだったら、 きちんと噛み砕いてわかりやすく説明することができる。
自分のことを、そう思っていた。
でも今日、このベレー帽をかぶった丸い眼鏡の女の子、ノナと話していて、なんだか考えが変わってきた。
僕がうまく教えることができるのは、 テトラちゃんやユーリに負うところが大きいのかもしれない。
テトラちゃんは、疑問点があるとさっと手を挙げて、自分が何を考えていて、どこがわからないかを的確な言葉にして教えてくれる。
ユーリは、的確な言葉じゃないこともあるけれど、ともかくわかったら《わかった》といい、わからなかったら《わかんない》といってくれる。
だから僕は、彼女たちの反応に導かれて語ることができたんだ。 彼女たちが、自分の状態を教えてくれるから、うまく教えることができた。
でもノナは……
ノナは、 いったいどんな考え方をしているのか、まだよくわからない。
だから、話すのがなかなか難しい。
さてさて、ここからどう進めばいいんだろう……
ノナ「……」
僕が黙っていると、ノナがまた険悪な表情になりつつあったので、僕は説明を再開する。
僕「《グラフを考える》っていったのは、こういうことだよ。 ノナちゃんが見ているのは《図として表した》グラフだよね。 でも、その同じグラフを《式として表す》ことができるんだ。 そのことについて考えてみようということ。 いまノナちゃんが見ている、ここに描かれているグラフ。 これを別の見方で見てみるんだ」
ユーリ「お兄ちゃん、また早口になってる」
ノナ「もう描かれているのに……考える $\NONAQ$」
僕「そうだよ。もう描かれているのに考えるというの、ノナちゃんは変に感じるのかな」
ノナ「……」
僕「もう少し話が先に進むとわかってくるかも。話を先に進めてもいい? 大丈夫?」
ノナ「大丈夫 $\NONA$」
僕「よかった。じゃあ、グラフの話に戻るね。グラフはこんなふうに一枚の紙に描くよね。 どこに何を描いているかわかるように、基準となる線を引いておくことにする。横と縦に直線を引く」
ユーリ「$x$ 軸と、 $y$ 軸」
僕「そうそう、ユーリのいう通り。直線にはそれぞれに名前がある。 横の線のことを $x$ 軸(えっくすじく)という」
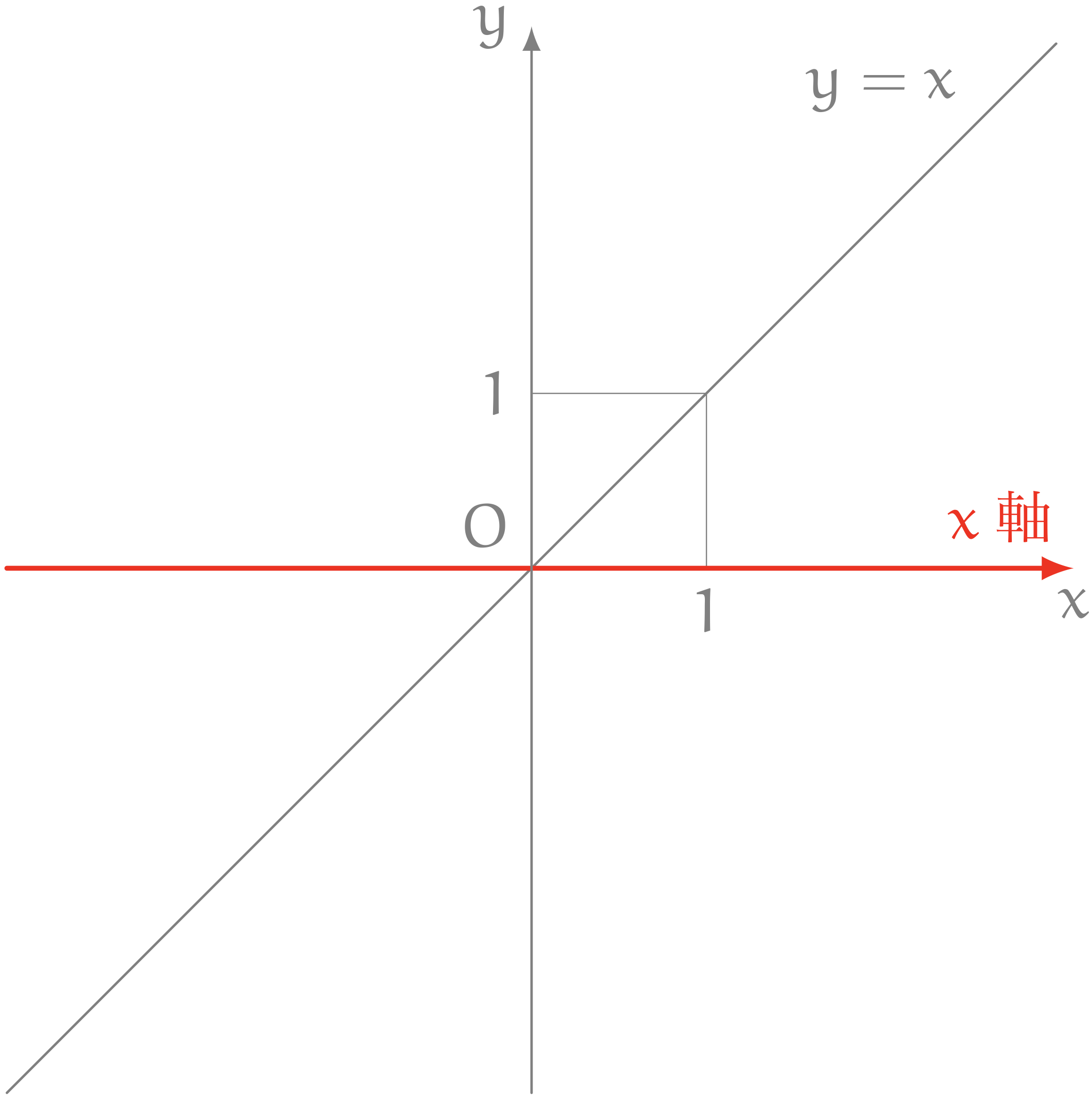
僕「それから縦の線のことを $y$ 軸(わいじく)ということが多い」
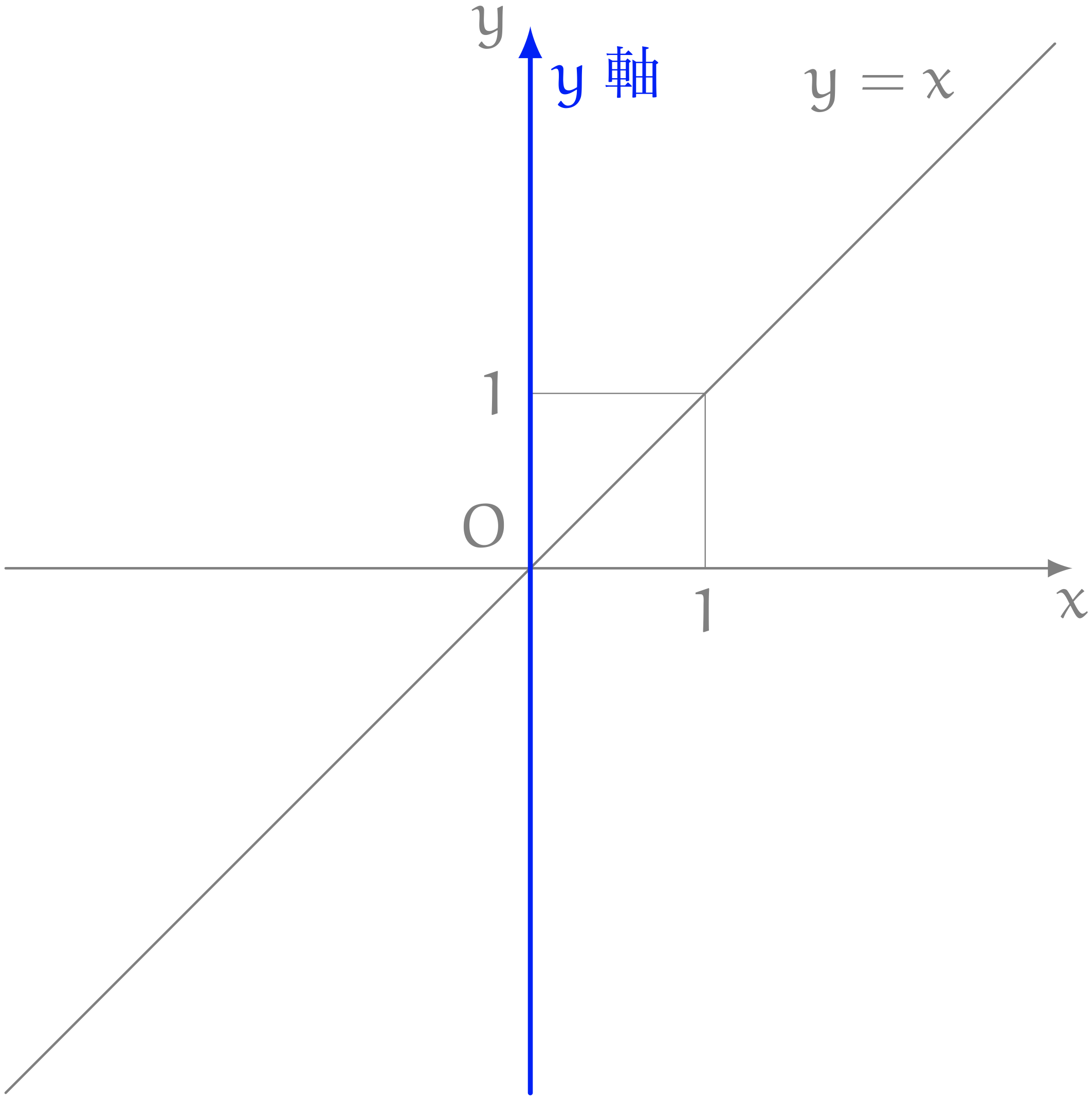
ノナ「これ、覚える $\NONAQ$」
僕「うーん、まあね。 でも、絶対にこうでなくちゃいけないってわけじゃないよ。 横の線はよく $x$ 軸にするし、 縦の線はよく $y$ 軸にするけど、 他のものになることもある。場合によるんだ。 大事なのは、基準になる直線が二本あって、それぞれに名前をつけておくというところ。 ここまで、大丈夫?」
ノナ「大丈夫 $\NONA$」
僕「大丈夫だったらいいけど、 わからない! とか、意味不明! になったら、 僕の説明途中でも、いつでも、そういっていいからね」
ノナ「大丈夫 $\NONA$」
僕「さっきは《紙》といったけど、 それはいま僕たちが見ているこれがたまたま《紙》だから。 《紙》には端っこがあるけど、 本当は、端なんてない。右にも左にも上にも下にも、どこまでもどこまでも広がっていると考えたい」
ノナ「無限に $\NONAQ$」
僕「そうだね! いわば、無限に続いていると考えたい。 それをはっきりというために、具体的に見える《紙》じゃなくて、 数学では《平面》という言い方をするんだよ。平面は、どこまでもどこまでも広がっている。 そこは、何でも描ける《無限のキャンバス》なんだ」
ノナ「無限のキャンバス $\NONAEX$」
僕「そう。無限のキャンバス。どんなに大きなものでも、自由に描くことができる場所だよ」
ノナ「無限のキャンバスは見えるの $\NONAQ$」
僕「それは難しい質問だなあ。数学の平面というのは、現実世界にあるものじゃないから、 その意味では目には見えないね。ただ、僕たちは平面の一部を切り取って、紙の上や、本の上にいろんな図を描いて、 これが平面だということにしよう! と約束する」
ノナ「見えないのに描ける $\NONAQ$」
僕「ノナちゃんは、絵を描くのは好き?」
ノナ「うん! 大好き!」
ユーリ「ノナはすっごく絵、うまいんだよー!」
僕「そうなんだ。ノナちゃんは絵を描くとき、実際に見て描くときもあるけど、目に見えないものを描くこともあるよね」
ノナ「お化け $\NONAQ$」
僕「お化けもそうだし、想像上の生き物や、物語に出てくる建物とか。 そういうものは目に見えないし、この世には存在しないかもしれない。 でも、それがどんなものかを伝えるために絵を描く。完全には描けないかもしれないけど、 何もないよりは伝わりやすくなる。絵や図にはそういう力があるよね」
ノナ「ユニコーンの角は一本 $\NONA$」
僕「そうそう、そういうこと。ノナちゃんは頭がいいね」
ノナ「ノナは頭わるいよ $\NONA$」
僕「そういうことは言わない方がいいよ。ともかく、 僕たちは《紙》の上にグラフを描くけど、実際には無限に広がっている《平面》の上にグラフを描いているんだ。 $x$ 軸と $y$ 軸の二つの軸がある、この平面のことを座標平面(ざひょうへいめん)という。 座標平面って聞いたことある?」
ノナ「覚えてない $\NONAX$」
僕「うん、じゃあ、いま覚えようか。難しそうな名前だけど、ただの名前だから。 座標平面って言ってみて」
ノナ「ざひょうへいめん $\NONAQ$」
僕「そうそう。新しい言葉を聞いたときや、聞き慣れない言葉が出て来たときには、 口で言ってみるといいんだよ。言葉に慣れるだけで、難しいって感じはなくなるから」
ノナ「ざひょうへいめん $\NONAQ$」
僕「そうだね。誰かと知り合いになるとき、最初に名前を聞くよね。 あなたの名前は何というんですか、みたいに。 それと同じなんだ。数学の勉強をするときには、たくさんの新しい言葉が出てくる。 いままで聞いたこともないような言葉がたくさん出てくる」
ノナ「暗記する $\NONAX$」
僕「うん、そう、言葉をたくさん覚える必要がある。 でも、その一つ一つは友達の名前のようなものなんだ。 だから、暗記しよう! と考えるよりも、 何度も口に出して慣れよう! と考える方がしっくりくると思うよ。 聞き慣れない名前や、見慣れない顔があると緊張するけど、 慣れることは大事なんだ」
ノナ「ざひょうへいめん $\NONA$」
僕「ノナちゃんは難しい話でも、一生懸命聞くんだね。えらいなあ」
ノナ「ユーちゃんと約束したから $\NONA$ ね?」
ユーリ「ね!」
僕「どんな約束?」
ノナ「ないしょ $\NONAHEART$」
ノナはそういって、にこっと笑った。
登場人物紹介(再度更新)
ノナ:ユーリの同級生。
ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。
数学は苦手だけど、興味を持ってる中学生。
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第241回終わり)
(2018年11月16日)
この記事は『数学ガールの秘密ノート/学ぶための対話』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!