第239回 シーズン24 エピソード9

群の働き（前編）

図書室にて

ミルカ「ラグランジュの定理を考えよう」

僕「剰余群や巡回群に限らず、有限群に対してこれが成り立つのか」

テトラ「有限群なら何でもいいという定理……それを考えるのは、どうすれば？　あたしは、やっぱり、具体例で考えたくなります」

ミルカ「ふむ」

テトラ「手のひらに乗るような《かわいい》有限群で、 でも巡回群じゃないもので、具体的だけど、数字に惑わされないようになっている、そんな群の例で考えたくなります」

僕「そんな都合がいい具体例は……あるね！」

テトラ「ありますね！」

僕「正 $6$ 面体群だ！」

テトラ「$4$ 次の対称群 $S_4$ です！」

僕「あれ？」

テトラ「あら？」

ミルカ「息がぴったり合ってるな」

僕「まあ、そうだね。同型だから」

テトラ「そ、そうですね」

僕「サイコロの置き方 $24$ 通りを台集合としても、 $ABCD$ の $4$ 個の順列 $24$ 通りを台集合としても、 二項演算をちゃんと合わせれば同型な群になるからね」

テトラ「そうですね。あっ、でも、台集合の要素の数が $24$ 個ということは、 $24 \times 24$ という大きな演算表を作らなくちゃいけなくなります……それは大変ですね」

リサ「ルールがわかればすぐにできる」

僕「リサちゃん！」

リサ「《ちゃん》は不要」

テトラ「……とはいえ、 $24\times24$ のように巨大な演算表を見て考えるのも難しいですね。 あまりにも大きいですから。あっ、でも、ありがとうございます」

僕「演算表は特に作らなくてもいいよ。 サイコロの置き方 $24$ 通りを $6 \times 4$ の表にするだけでいける」

僕「$1$ 行目は、上の面が $1$ になったサイコロを $\KAKUDO{90}$ ずつ回転させたもの。 これを部分群だと思って、この表の残りの $5$ 行に剰余類を入れていくんだ」

テトラ「ええと……」

僕「うん、こんなふうになるよ」

テトラ「これは、どういう配置なんでしょう」

僕「横に見ていくと、上の面が同じものが並んでいるよね。 $1$ 行目は上の面が全部 $1$ になっていて、 $2$ 行目は上の面が全部 $2$ になっている……という具合」

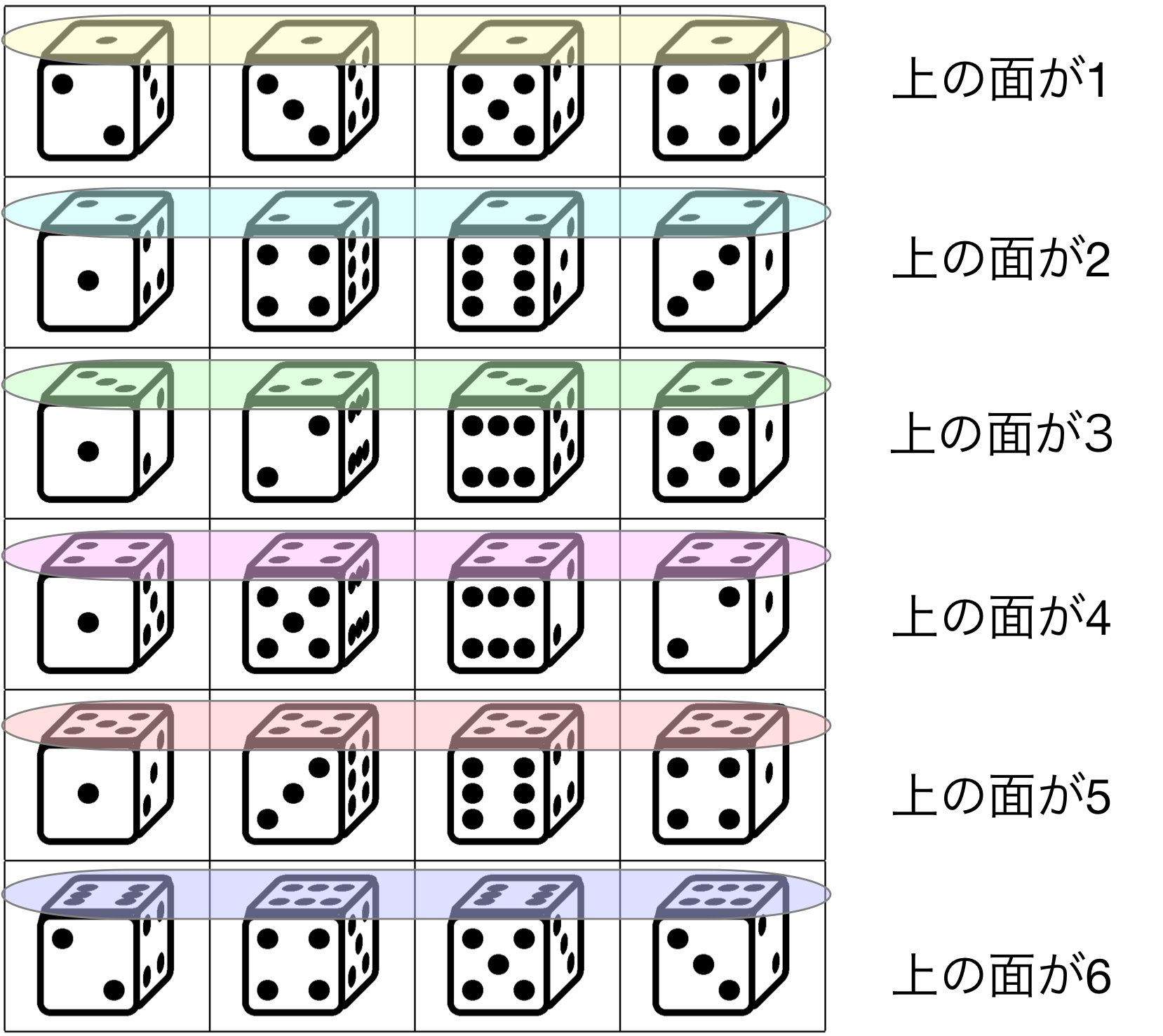
テトラ「確かにそうですね」

僕「そして、どの行をみても、 $1$ 行目と同じように $\KAKUDO{90}$ ずつ回転したものになっているということ」

テトラ「なるほど……規則的なパターンがありますね！　ところで、 これで本当にラグランジュの定理を考えるための例になっているんでしょうか」

ミルカ「同型な群は同じ名前で呼ぶことにしよう。 彼がやろうとしているのは《$4$ 次の対称群 $S_4$》を、 その部分群である《巡回群 $C_4$》で割った剰余類を作ることだろう」

僕「そうだね、そうなる。 このサイコロ $24$ 通りを台集合とした群の全体は《$4$ 次の対称群 $S_4$》と同型になっているよね。 そして、その部分群として位数が $4$ の《巡回群 $C_4$》を考えることができる。この図でいえば、 $S_4$ と $C_4$ はここにあるよね」

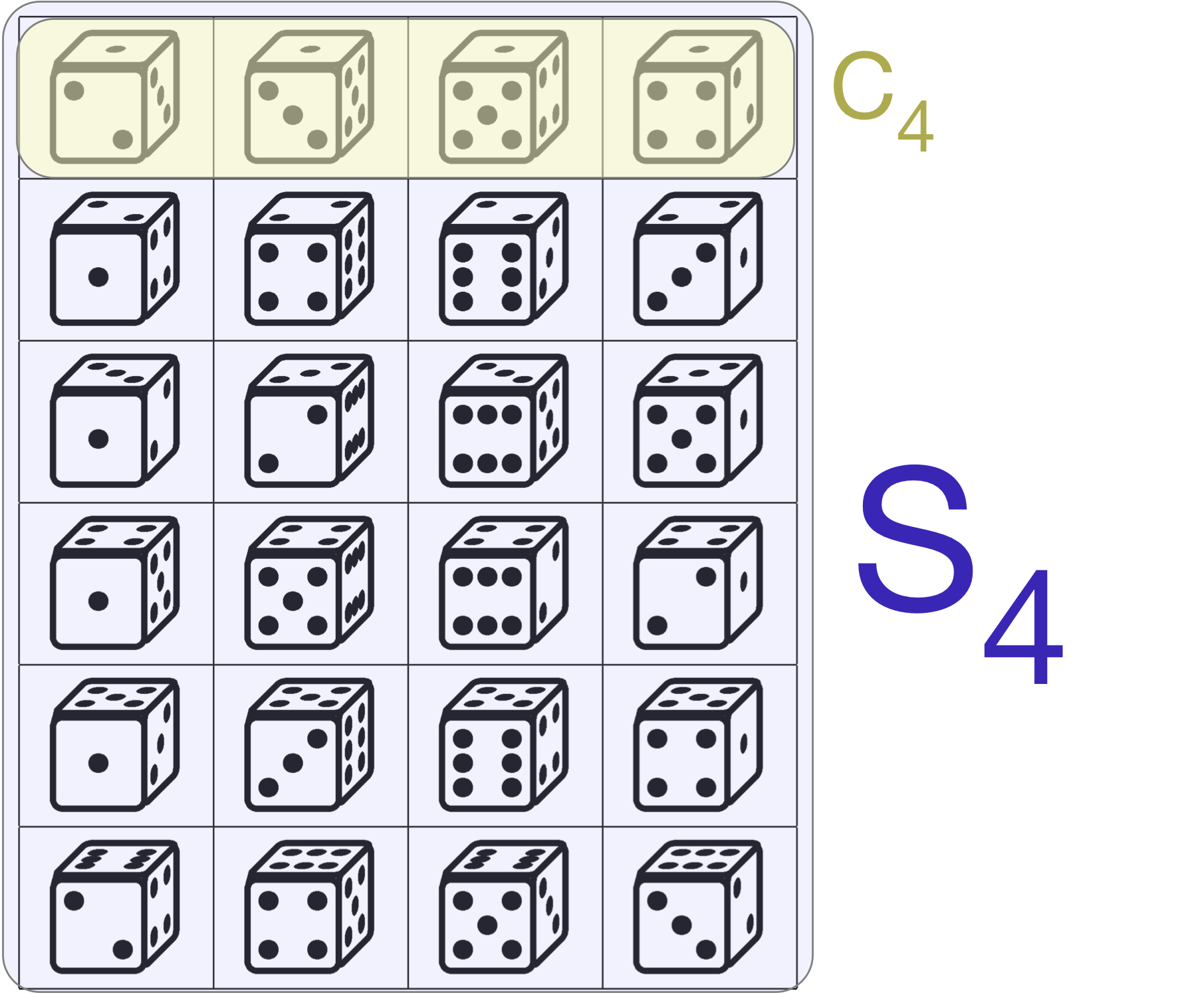
テトラ「なるほど……」

僕「そして、さっき僕たちが考えていた類別と同じものが、ちょうどこの表に現れているよ。 僕たちが考えていたのは、 《有限群を、その部分群を使って剰余類に類別する》ということだったよね」

テトラ「はい、これのことですね（第238回参照）」

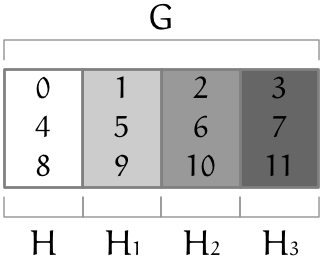
僕「うん、それと同じだよ。 《対称群 $S_4$ を、その部分群 $C_4$ を使って剰余類に類別する》 結果になってるんだ！　剰余類ごとに色分けするとはっきりするよ」

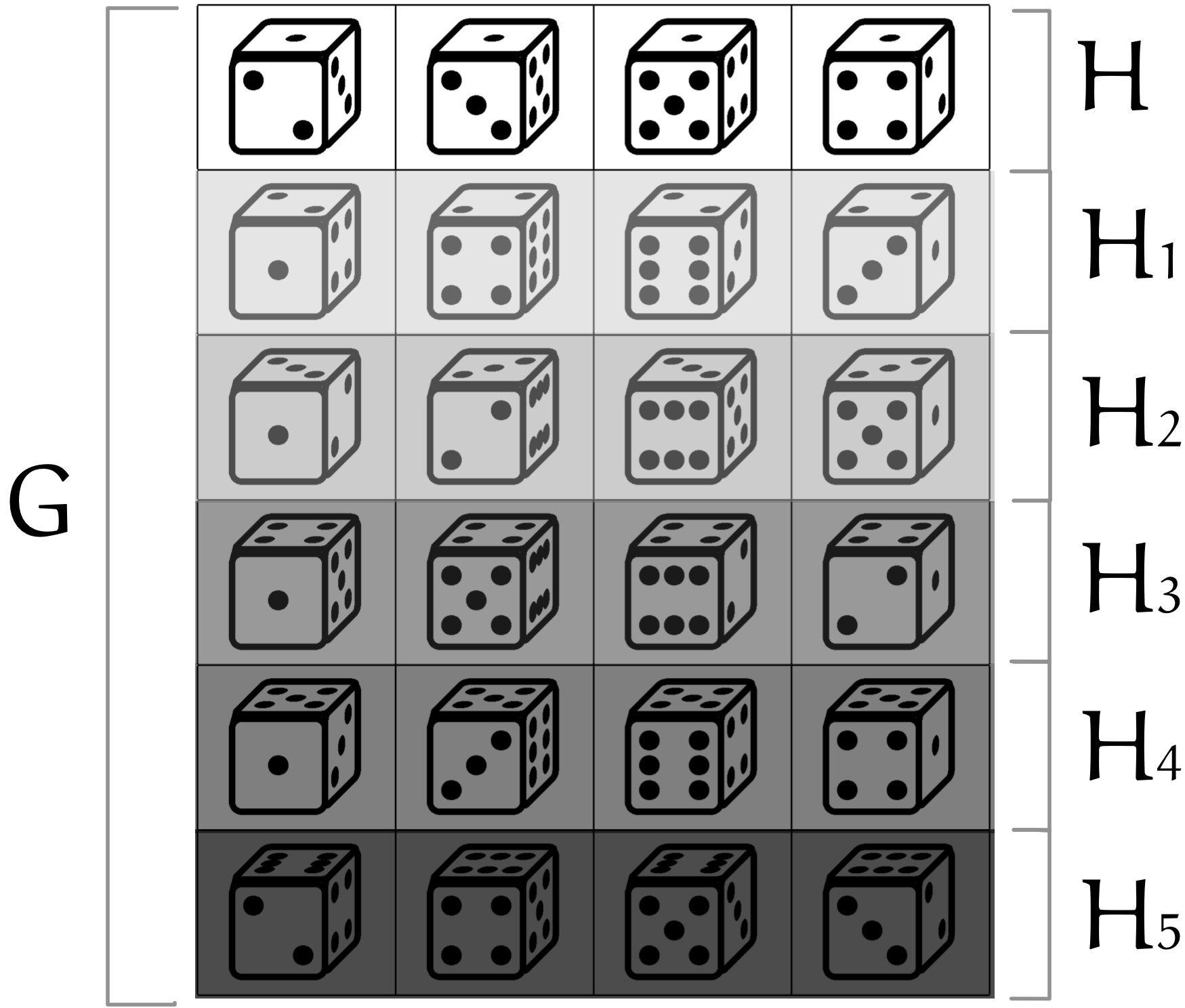
テトラ「ああ、縦横が変わりましたけど、理解しました！　全体が $G$ に相当して、 $1$ 行目が $H$ に相当するのですね」

僕「しかも、それぞれの《剰余類の要素数》は《部分群 $C_4$ の位数》に等しいこともわかるね。つまり、ここでは $4$ 個ということだけど」

テトラ「なるほど！　確かにこれはあたしたちが考えたいことの例になっていますね。 巡回群じゃない群があります。ここでは対称群 $S_4$ です。 そしてその部分群 $C_4$ を使って類別ができました。 この例を見ると《剰余類》のイメージがだいぶつかめてきました。特に《類》の部分です。 この表の各行が《剰余類》で、たとえば $2$ 行目の例ですと《上の面が $2$ になっている》という置き方がここに集まっていますよね。 つまり同類が、共通点を持つ同じ仲間がここに集まっています」

僕「そうだね。確かに同類だ」

ミルカ「テトラは剰余類の《内部》に注目した。剰余類の《外部》にも注目しよう」

テトラ「剰余類の《外部》といいますと？」