第234回 シーズン24 エピソード4

転んだ椅子（後編）

僕の部屋

ユーリ「……おもしろーい！　なにこの《うまくはまる》感じ！　《あたりまえ》っぽいのに《不思議》な感じ！」

僕「おもしろいよね。

• サイコロの置き方 $24$ 通り
• 机の上に来る頂点の並び方 $24$ 通り
• 対角線の並び方 $24$ 通り
• $ABCD$ の順列 $24$ 通り

ユーリ「同じものを……別の目で」

僕「そうだよ。僕たちはサイコロの置き方に $ABCD$ のように名前を付けた。 でもそれは適当に付けたわけじゃない。並びに意味がある。 だからこそ、サイコロの置き方の変化が、名前の変化とうまく呼応しているんだね」

ユーリ「ふーん……そっか、たとえばこれもそーだね。 $A,B,C,D$ の $4$ 個が全部ズレていくパターン！」

僕「ああ、そうだね。これは面の中心を通る回転軸での回転だね」

ユーリ「……」

僕「……」

ユーリ「ねーお兄ちゃん、気付いたことあるんだけど……」

僕「何？」

ユーリ「あのね……サイコロの面があって、その中心を通る回転軸だと、 $4$ 回で元に戻るよね」

僕「そうだね」

ユーリ「面の中心を通る回転軸だと、 $4$ 回で元に戻るけど、 それって《サイコロの面が、正 $4$ 角形だから》だよね」

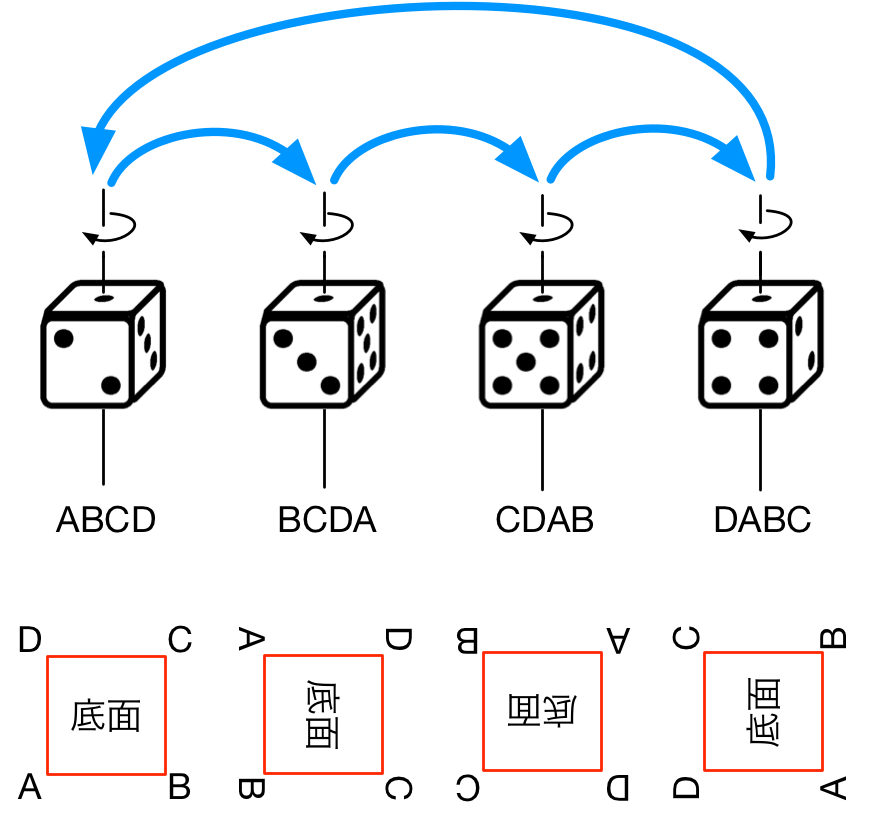
僕「うん、確かにそういうことになる。正方形……正 $4$ 角形を $90$ 度回したとき、ちょうど自分自身と重なる。 そして、 $90$ 度回転が $4$ 回で $360$ 度。元に戻る」

ユーリ「面の中心で回転すると、 $4$ 回で元に戻るってゆーのは、《面》が正 $4$ 角形だから。 でね、頂点を結ぶ対角線で回転すると、 $3$ 回で元に戻るじゃん。 それって《ここ》に正 $3$ 角形があるからだよね！」

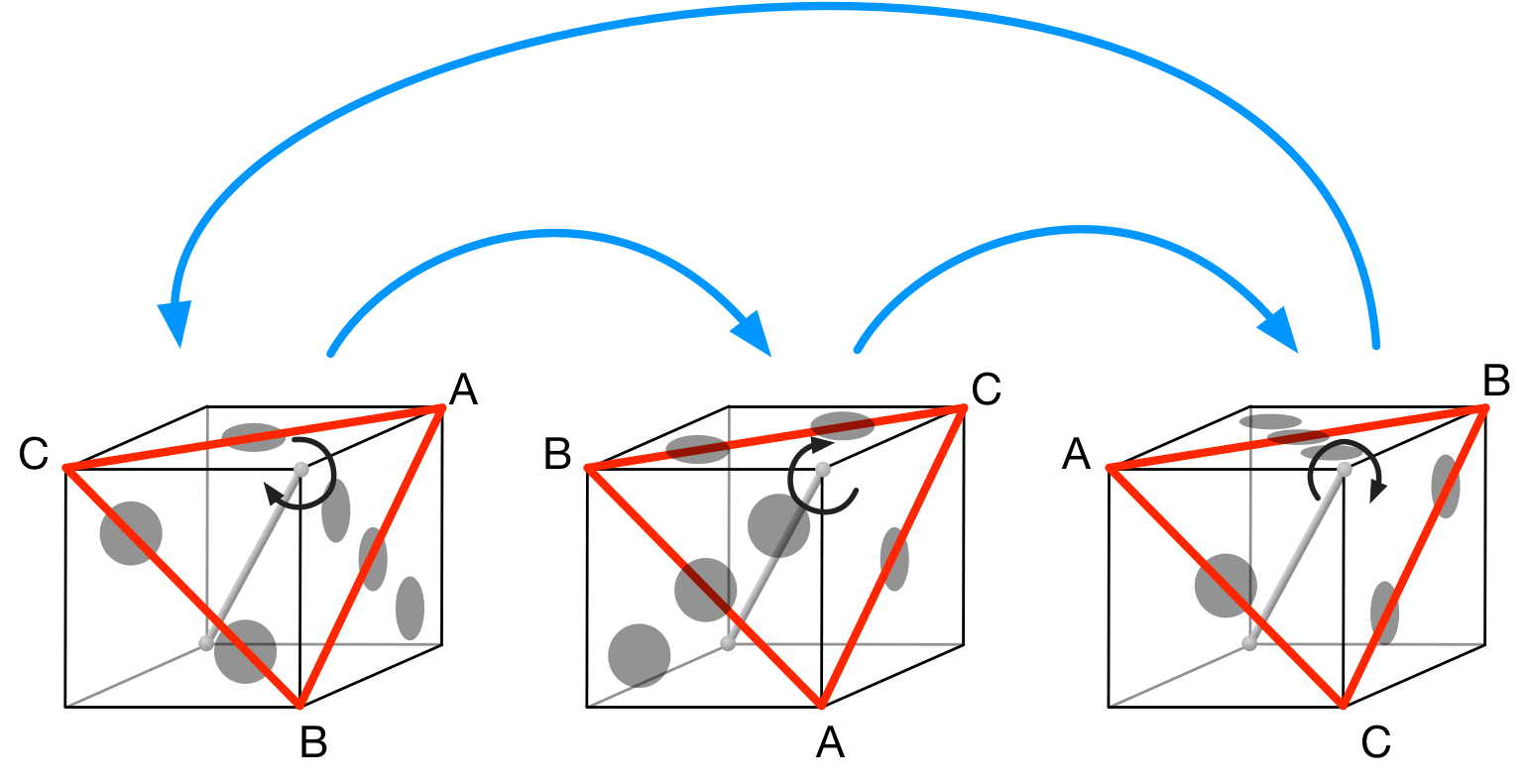
僕「なるほど」

ユーリ「あれ、何で感動しないの？　『ほんとにそうだね。ユーリは賢いなあ！』って言ってくんないの？　これ、正 $3$ 角形だよね？だって正方形の対角線だもん」

僕「いやいや、ユーリは賢いよ。確かにこれは正 $3$ 角形になるし。 いまはちょっと、ユーリが言ってたことを考えてただけなんだ。 立方体の対角線で回転したときに $3$ 回で元に戻るのは、《そこに正 $3$ 角形があるから》なのかなって……」

ユーリ「違うの？」

僕「《正 $3$ 角形があるから、 $3$ 回で戻る》のか《$3$ 回で戻るとき、そこには正 $3$ 角形が見つかる》のどっちなのかな……って考えていたんだ」

ユーリ「うわなにその微妙な話！」

僕「それはそれとして、正 $6$ 面体の中にある正 $3$ 角形を見つけるというのは楽しいな」

ユーリ「でね、でね、話はまだあるの。 面の中心で回すと $4$ 回で戻る。頂点で回すと $3$ 回で戻る。 辺の中点を通る回転軸のときは、 $2$ 回で元に戻るでしょ？」

僕「そうだね。表と裏をひっくり返すように」

ユーリ「$2$ 回で元に戻るのは《サイコロの辺が、正 $2$ 角形だから》っていえる！」

僕「サイコロの辺が、正 $2$ 角形！　……ふつうはそうはいわないけど、確かにユーリの考えは正しいぞ。 線分の両端を角度が $0$ 度の角だと見なすなら、いわば正 $2$ 角形だ！」

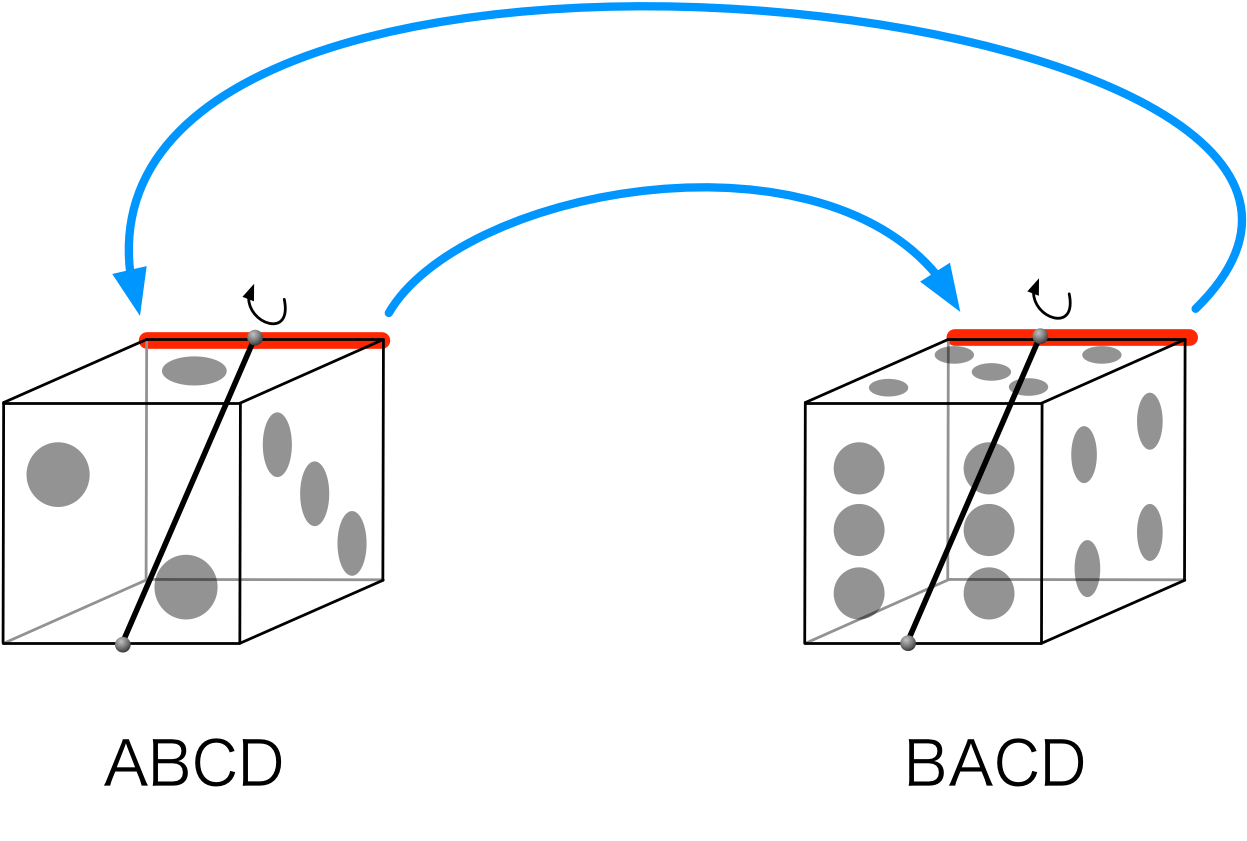
ユーリ「これってすごくない？」

僕「すごいすごい。ユーリのその発想はすごいなあ。《$n$ 回で元に戻るところに正 $n$ 角形あり》ということなんだね。 ユーリはほんとに賢いなあ」

ユーリ「へへ」

僕「ユーリは回転で不変な形に注目していたことになるね」

ユーリ「ふへん」

僕「ほら、ミルカさんがよくいう《不変性》のことだよ。 何かを変化させたとき、もしも不変なものがあったらそれに注目する。 不変なものは大事なことを教えてくれることがある」

ユーリ「不変なもの……」

ユーリ「ねーお兄ちゃん。さっきの話でちょっと気付いたことがあるんだけど」

僕「さっきの話」

ユーリ「面の中心で回して $4$ 回で戻るのは、長いのをつぶしてもいーからだよね」

僕「つぶしてもいい？」

ユーリ「なんてゆーか……正 $6$ 面体のサイコロを一枚に、ぺしゃんとしてもいーよね？」

僕「ああ、そういうことか。そうだね。つぶしても $4$ 回で戻るようすは同じといえる。イメージとしてね」

ユーリ「つぶすのを逆にして、引き延ばしてもいーよね」

僕「ははは！確かにね。 ユーリがいま言った《○○してもいーよね》というのは、 《○○したとしても、 $4$ 回で元に戻るという性質は変わらない》……という意味なんだね」

ユーリ「さっきからそー言ってるじゃん」

僕「いや、言ってはいないよ……」

ユーリ「正 $4$ 角形は $4$ 回で元に戻るんだけど、それじゃなくても《$4$ 回で戻る》仲間はいっぱいあるって言いたいの」

僕「うん。それは深い話だな。形の対称性の話だね（第232回参照）。 回転軸方向につぶしたり、引き延ばしたりしても、同じ仲間のまま。 もちろん、引き延ばしたら立方体じゃなくなるから、他の回転軸では回せなくなるけど」

ユーリ「それはわかってるの！ うーん……あんまりおもしろい話じゃなかった？」

僕「いやいや、そんなことないよ。 ユーリはそんなふうにつぶしたり引き延ばしたりしてみたかったんだね」

ユーリ「そだよ。それでね。サイコロの形……正 $6$ 面体ってゆーのは、 そゆのをぜんぶ集めた対称性を持ってるのかにゃー……って考えてたの」

僕「んんん？　いま大事そうなこと言ったね。ユーリ、もう一度言って？」

ユーリ「回転軸が $1$ 本だと、さっきみたいにつぶしたり引き延ばしたりできるじゃん？ 回転軸が $3$ 本あると、そうも行かない。 だから、ちょうどいい形になったところが正 $6$ 面体なのかなー……あーもー、うまく言えにゃい！」

僕「いや、ユーリの言いたいことがわかってきたよ。 正 $6$ 面体では、面の中心を通る回転軸は $3$ 本あって、 $3$ 本のどれを使っても、 $90$ 度回したところで自分自身と重なる。 そして $4$ 回まわしたら元に戻る。 そんな立体は正 $6$ 面体に限るんじゃないかってことだろうか」

ユーリ「うん！そーでしょ？」

僕「いや、そうじゃないよ」

ユーリ「？」

僕「直交する $3$ 本の直線があって、それを $3$ 本の回転軸だと考えることにする。 正 $6$ 面体のサイコロと同じように、回転軸を使って $90$ 度回すごとに、自分自身とぴったり重なる立体があったとする。 もちろんその立体は同じ軸を $4$ 回まわすと元に戻る……そういう立体は正 $6$ 面体のサイコロ以外にもあるよ」

ユーリ「ほんとに？」