![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリはサイコロの置き方についておしゃべりをしている。
面を東西南北に向ける《サイコロの置き方が $24$ 通りあること》と、 《$4$ 個のものを並べる順列が $24$ 通りあること》の関係を調べているところ((第231回参照)。
ユーリ「いやー、うまく行くもんだねー。 お兄ちゃんが言ってた《頂点に $A,B,C,D,A',B',C',D'$ と名前を付ける》 ってゆーの、おもしろいね!」
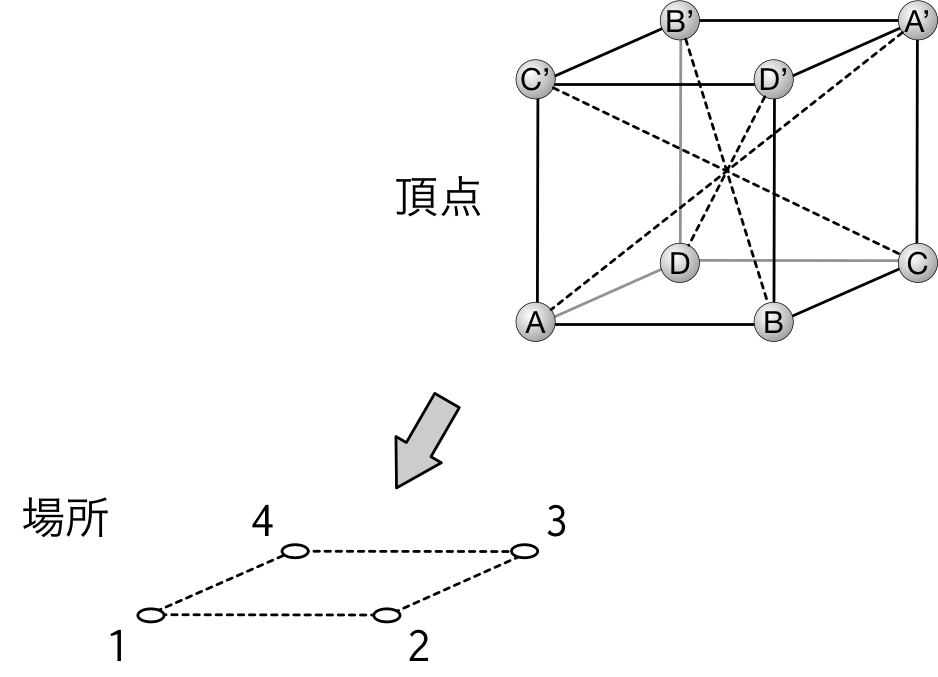
僕「そうだね。頂点に $A,B,C,D$ という名前と、 $A',B',C',D'$ という名前を付ける。 $A$ と $A'$ は同じ種類の頂点だと考えた上で、サイコロを机の上に置く。 机には頂点が置かれる $4$ 個の場所がある。サイコロの置き方は $A,B,C,D$ という $4$ 種類の頂点がどの場所に来るかにちょうど対応している。 だから、サイコロの置き方 $24$ 通りは、 $4$ 個を一列に並べる順列の数になっていることがわかる……」
ユーリ「$24$ 通り全部確かめたもんね!(第231回参照)」
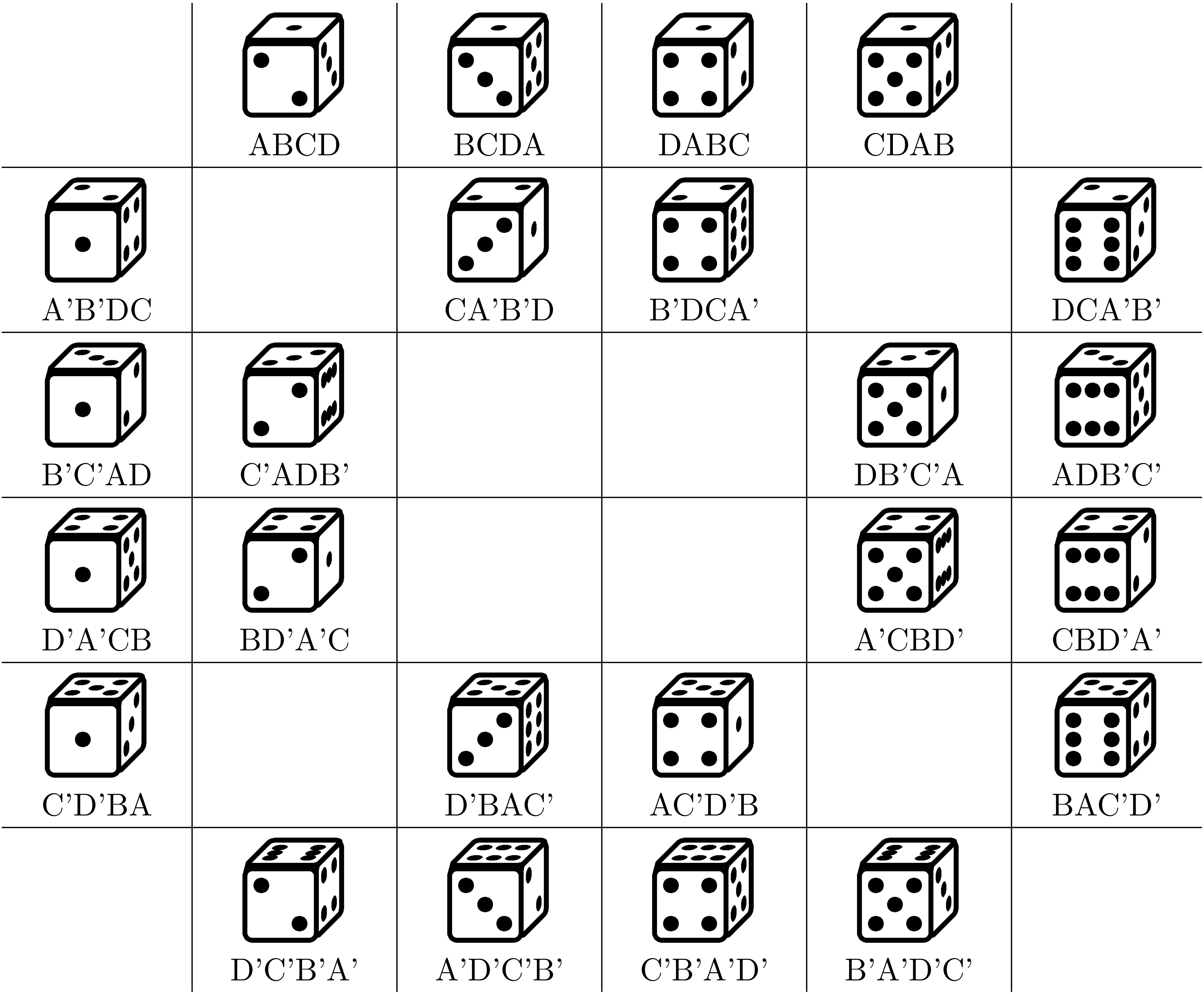
サイコロの置き方 $24$ 通りと、机に接している頂点の名前
僕「でも、まだ、完全には《わかった感じ》がしないなあ」
ユーリ「そう?」
僕「うん。ユーリが気付いた $24 = 4 \times 3 \times 2 \times 1$ という事実はなかなか冴えていたよ。 そして、すべての場合を確かめたから《もれなく、だぶりなく》対応が付いていることはわかる。 でもね、立方体の頂点に名前を付けてくるくる回したときに、 $A,B,C,D$ の順列がどうして《もれなく、だぶりなく》出てくるのか、うまく説明はできない……まだ」
ユーリ「全部確かめたのに?」
僕「どうしてそうなるか、もう一歩踏み込みたいよね」
ユーリ「ふーん……ところでさー、場合の数を考えるときって、いつも階乗が出てくるよね」
僕「いつも? いまユーリ、《いつも》って言った? 《いつも》とは限らないよね。それは《誤った一般化》だよ」
ユーリ「突っかかるにゃあ……だって、 $4$ 個のものを一列に並べる場合の数は、 $$ 4! = 4 \times 3 \times 2 \times 1 $$ 通りあるじゃん。これが階乗でしょ」
僕「そうだね。順列の個数は階乗になる。それから組み合わせでも階乗が出てくる。 $n$ 個のものから $r$ 個を選ぶ場合の数は、 $$ \frac{n!}{r!(n-r)!} $$ になる。だから階乗を使って表せる。 確かにユーリがいうとおり階乗が出てくることは多いよ。《いつも》とは限らないけど」
ユーリ「それって何で?」
僕「何で、とは?」
ユーリ「場合の数を考えるとき、階乗がよく出てくるのは何で?」
僕「うーん、《何で》と言われても困るなあ」
ユーリ「そこをなんとか説明」
僕「場合の数では何かを並べて考えることがよくあるよね。 つまり、順列はとても基本的なもの。 そして、順列では並べていく途中で、 並べられるものが一つずつ減っていく」
ユーリ「やっぱ説明はいーや」
僕「直感的には樹形図を考えると納得するよ」
ユーリ「じゅけーず」
僕「樹形図は、場合の数を《もれなく、だぶりなく》考えるための道具の一つだよね。 $A,B,C,D$ という $4$ 個のものを並べる順列はぜんぶ列挙できるけど、 ただ並べるよりも樹形図にした方がまちがいは少ない」
列挙
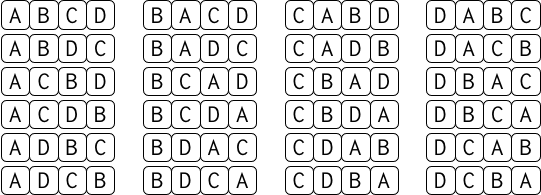
樹形図

ユーリ「あー、そだね」
僕「樹形図を左から順番に見ていくと、最初の枝分かれは $4$ 本ある。 これは、最初に置くのが $A,B,C,D$ の $4$ 通りあるから。 そして、そのそれぞれに対して次の枝分かれは $3$ 本ある。 $4$ 本が $3$ 本に減ったのは、次に置けるのが $3$ 通りに減ったから」
ユーリ「最初に置いたのは使えないから」
僕「そういうこと」
ユーリ「そっか。だから掛けるものが一つずつ減っていく……それで階乗が出てくる。それだけの話?」
僕「そうそう。場合の数では順列がよく出てくる。 そして順列は階乗を使ってうまく計算できる。 それは、 端から置けるものを順番に決めていって、 置いていくたびに、次に置けるものが一つずつ減っていくという具合だね」
ユーリ「サイコロも?」
僕「え?」
ユーリ「サイコロの置き方が $4$ の階乗になるのも、 次に置けるものが一つずつ減っていくからなの?」
僕「おっと!……ちょっと待って」
僕はユーリの言葉をきっかけに、頭の中でサイコロをくるくると回す。
ユーリ「ねー……」
僕「確かに! $4$ 個の並べ替えにこだわらないで、素直に数えればわかるんだ。 $4$ 通りのそれぞれに対して $3$ 通り、確かにあるなあ! うんうん」
ユーリ「ねー! 一人で納得しないでよー」
僕「ごめんごめん。 ユーリがくれたヒントはなかなかいいよ。 僕たちはいま、サイコロの置き方について考えている」
ユーリ「$4! = 24$ 通り」
僕「そうだね。机に描いた $1,2,3,4$ の場所に対して、 $A,B,C,D$ のどの頂点が来るかを考える。 サイコロには $8$ 個の頂点があるから、 わかりやすく区別するために $A,B,C,D,A',B',C',D'$ と名前を付けたけど、 気持ちとしては $A$ と $A'$ を同じ種類の頂点だと見なして、 $A,B,C,D$ の $4$ 個のものを並べ替えているつもり」

ユーリ「そんで?」
僕「さっきの樹形図と同じように考える。 つまり、場所 $1$ に来ることができる頂点は $A,B,C,D$ の $4$ 種類がありうるよね」
ユーリ「オッケー。どんどん進んでよ」
僕「それで場所 $1$ に置く頂点は決まった。仮に $A$ だとしよう。 そのとき、場所 $2$ には $A$ 以外の頂点 $B,C,D$ の $3$ 種類がどれも来ることができるかな、と考える」
ユーリ「にゃるほど。樹形図といっしょで、一つ減ったんだね」
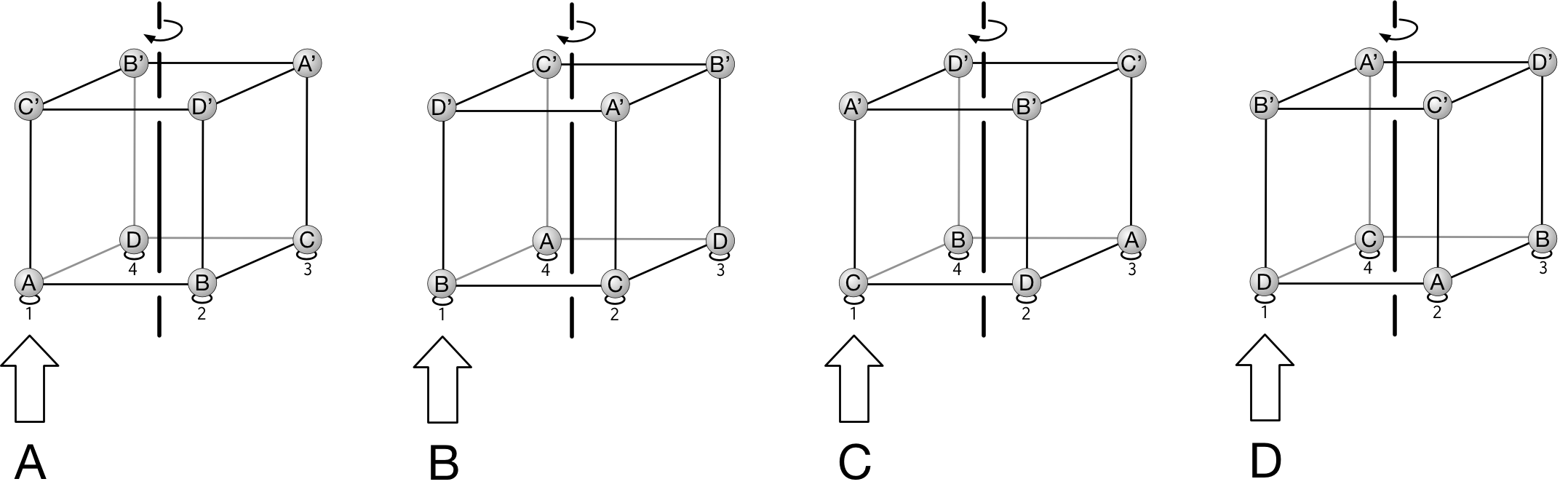
僕「そして実際、場所 $2$ には、 $3$ 種類のすべてが来ることができる。 それは、《$A$ と $A'$ を結んだ対角線を回転軸とした回転》を考えればいいんだ! そうすれば、場所 $1$ に頂点 $A$ を置いたままで、場所 $2$ には $B,C,D$ という $3$ 種類の頂点を持ってくることができる」
頂点 $A$ と $A'$ を結ぶ対角線を回転軸とした回転

ユーリ「ほほー! 斜め攻撃ですか」
僕「頂点への名付け方を考えると、 $A$ から辺 $1$ 本分離れたところにある頂点は $B,C',D$ の $3$ 通りがあるから、 場所 $1$ に $A$ を置いたままで場所 $2$ に来ることができる頂点は確かに $3$ 種類あるわけだね。《もれなく、だぶりなく》$3$ 種類がある」
ユーリ「てことは、場所 $1$ と場所 $2$ に来る頂点が決まったところで、 $4 \times 3$ 通りある! ……でも、階乗を作るためには、次がだめじゃん!」
僕「だめって?」
ユーリ「だって場所 $1$ と場所 $2$ に来る頂点が決まったら、 場所 $3$ は決まっちゃうよ? たとえば、場所 $1$ に頂点 $A$ を置いて、場所 $2$ に頂点 $B$ を置いたら、場所 $3$ は頂点 $C$ に決まっちゃうもん」
僕「ユーリは飲み込みが早いなあ。でも、大丈夫。 場所 $3$ に置ける頂点はちゃんと二種類ある。 $C$ と $D$ の $2$ 種類の頂点を場所 $3$ に置けるんだよ。 $A$ には $A'$ が、 $B$ には $B'$ があるからね。 サイコロを回して、ちょうど辺 $AB$ と辺 $A'B'$ を交換すればいい。 そうすると、場所 $1$ と場所 $2$ に置く頂点の種類は $A$ と $B$ に固定したまま、 場所 $3$ に $C$ と $D$ の $2$ 種類をどちらでも持ってくることができるんだ!」
ユーリ「……」
僕「ここまでで、場所 $1,2,3$ に置ける頂点が決まった。そして場所 $4$ に置ける頂点は自動的に決まる。 これで、 $4\times3\times2\times1$ が作れたね。階乗になった」
ユーリ「納得いかにゃい!」
僕「え、そう? $4$ 通り選べるのは、上下を結ぶ軸の回転があるから。 $3$ 通り選べるのは、対角線を軸とする回転があるから。 $2$ 通り選べるのは、反転できるから。 まとめると……」
ユーリ「場所 $1$ と場所 $2$ はナットク。でも場所 $3$ はナットクできーん!」
僕「場所 $3$ が納得できない?」
ユーリ「お兄ちゃんは《辺 $AB$ と辺 $A'B'$ の交換》で話を終わらせたけど、 おかしいよー。お兄ちゃんは、辺 $AB$ を辺 $A'B'$ に変えるっていったけど、じゃ辺 $AB'$ や辺 $A'B$ は?」
僕「いやいや、 $AB'$ や $A'B$ なんて辺はないから。 $A$ と $B$ という $2$ 種類の頂点を使った辺というのは、 $AB$ と $A'B'$ の $2$ 通りしかないんだよ」
ユーリ「えっ……あ、ほんとだ」
辺 $AB$ と辺 $A'B'$
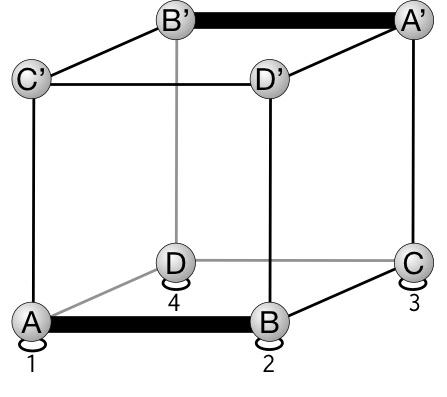
僕「だから、 $\prime$ のあるのとないのとを反転させるのは $2$ 通りなんだ」
ユーリ「うーん……なんかまだ、ごちゃついてるんだよー」
僕「うーん……まだ納得できないか……」
ユーリ「もう一声、バシッと決めて欲しい」
僕「……じゃ、こういうのはどうだろう。 サイコロをこんなふうに二つに分けるんだ。 《左手の世界》と《右手の世界》のように」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年8月10日)