第223回 シーズン23 エピソード3

平均値の定理（前編）

どうして平均？

テトラ「なるほど……おもしろいお話ですねえ」

僕「だよね。時刻に対する《位置のグラフ》が、 かくっと折れているところは時刻で微分できないという話」

テトラ「あたしが特におもしろいと思ったのは、 《瞬間の速度》を定義していくところでした。 《瞬間の速度》というと、いったいどんな意味なのかよくわかりませんけれど、 よくわかっている《平均の速度》を使って、 《瞬間の速度》というのはどんな定義であってほしいか を考えていくところです」

僕「そうそう。そして定義できてみれば、 かくっと折れているところの《瞬間の速度》 が決まらないのは《あたりまえ》に見える。 ユーリも『あったりまえじゃん！』なんて言ってたよ」

テトラ「それにしてもユーリちゃんは、 いろんなことをパッと理解してしまうんですね。 すごいです」

僕「そうだね。 でもさすがに微分は《パッと理解》という感じでもなかったかな。 定義を何度も読み返して、じっくり考えてたよ。 《平均の速度》が二つの異なる時刻 $t_0$ と $t_1$ で決まることに感心していたなあ」

テトラ「そうなんですね。 あたしはお話の中で《平均の速度》という言葉が気になっていました」

僕「え、そうなの。《平均の速度》っていうのは、時刻 $t_0,t_1$ での位置をそれぞれ $x_0,x_1$ としたときの、 $\frac{x_1 - x_0}{t_1 - t_0}$ のことだけど」

テトラ「あ、いえいえ。《平均の速度》の定義はあたしもわかります。 でもそれをどうして《平均》と呼ぶのかなあ……と気になるんです」

僕「そうなんだ」

テトラ「あのですね。《平均》というのは、いつもの平均ですよね。 全員のテストの点数を足して人数で割ったのが平均点。 あの平均と同じですよね？　合計点を人数で割るのと、 《平均の速度》とどこが同じなんでしょう」

僕「ああ、なるほど。《平均の速度》という概念のことじゃなくて、 どうしてその概念に《平均の速度》という名前が付いているかということ？」

テトラ「そうです、そうです」

僕「それは簡単だよ。テストの平均点の話でも、 《平均の速度》の話でも、どちらも均している（ならしている）わけだから」

テトラ「均している……テストの平均点の方はわかります。 点数の高い人がいたり、点数の低い人がいたりします。 いろんな点数を取っている人がいますけど、 その点数のでこぼこをなくして、 均一にしたならどんな点数になるか……それが平均点ですから」

僕「そうだね、テトラちゃんの言う通り。 《平均の速度》もまったく同じだよ。 時刻 $t_0$ から時刻 $t_1$ のあいだに、位置が $x_0$ から $x_1$ に移動したとする。 その途中はどんな動きをしているかわからない。 サッと速く動くときもあれば、ゆっくり動くときもあるかもしれない。 ときどき逆向きに動いたりするかも。 $t_0$ から $t_1$ のあいだ時間に起こっていることの話だよ」

テトラ「ははあ……」

僕「でも、その速さや向き……つまり速度のでこぼこをなくして、 均一の速度で移動したとしたら？　それに答えるのが《平均の速度》なんだよ。 ね、平均点と同じだよね？」

テトラ「なるほどです！　確かにそうですね！　ああ、すっきりしました」

僕「それはよかった」

テトラ「あたし、授業を聞いているときでも、ときどきこうなります」

僕「こう？」

テトラ「はい。 『どうして《それ》のことを《そう》呼ぶんだろう？』 って気になるんです」

僕「なるほどね。以前もそういう話、してたね。 疑問は疑問として、授業中は先生の話を聞いていた方がいいと思うけど」

テトラ「あ、はい。先輩からも以前そういわれたので、 注意するようにしています。ノートにメモしておいて、後で考えるように……できるだけ」

僕「《平均の速度》だから、 $\frac{x_1 - x_0}{t_1 - t_0}$ という形になるけど、 それを一般化して似たような概念を考えることもできるよ」

テトラ「似たような概念……ですか」

僕「うん。《時刻 $t$ に応じて位置 $x$ が変化する》というのは物理学の話だけど、 時刻や位置から離れて考えるんだ。 たとえば《実数 $x$ の値に応じて実数 $y$ の値が変化する》というふうに考えれば一般化したことになるよね」

テトラ「はい、わかります。それは関数ですね」

僕「その通り。 実数 $x$ の値に応じて実数 $y$ の値が一つ必ず決まると考えれば、 $y$ を $x$ の関数として考えていることになる。実数全体の集合から実数全体の集合への関数 $f$ を考えているんだね」

テトラ「$x$ の値に応じて $f(x)$ の値を考える……ですね」

僕「そういうこと。その上で《平均の変化率》を考えることができる。 つまり、 $\frac{f(x_1) - f(x_0)}{x_1 - x_0}$ という式の値を考えるわけだね」

テトラ「……」

僕「あれ？　これはテトラちゃんには難しい話じゃないよね？」

テトラ「あ、はい。大丈夫です。 $x_0, x_1$ で、一瞬あれっと思っちゃいましたが、 大丈夫です。《平均の速度》では $t$ に対して $x$ が変化していましたが、 今度の《平均の変化率》では $x$ に対して $f(x)$ が変化しているのですね？」

僕「そうそう。文字の役割が変わったね。式が表しているのは同じことだけど。 変化するものが二つあって、変化前と変化後での差を調べてその比を取っているだけのことだから」

テトラ「はい、大丈夫です」

平均値の定理

僕「《平均の変化率》で思い出したけど、 微分を習うときに出てくる平均値の定理という定理があるんだよ。 こんな定理」

テトラ「平均値の定理」

僕「そうだね。ほら、平均値の定理が主張していることの中に、 $$ \frac{f(b) - f(a)}{b - a} $$ という形が出てきているよね。さっき話した《平均の変化率》の形になっている式」

テトラ「ははあ……ええと、この式は、 $x$ が $a$ から $b$ まで変化するときに、 $f(x)$ がどれだけ変化しているかを考えている式ということでしょうか」

僕「だいたいはそういうこと。でももう少し正確にいうと、 《$f(x)$ がどれだけ変化しているか》を表しているのは $f(b) - f(a)$ の部分だよね。 $f(b) - f(a)$ だけを考えるんじゃなくて、 $f(b) - f(a)$ を $b - a$ で割っていることも忘れないでね。 だから変化じゃなくて変化率という言い方をしてるわけだし」

テトラ「あっ、そうです。そういうことを言いたかったんでした」

どういう定理？

テトラ「ところでこの平均値の定理って、どういう定理なんでしょうか。 見てすぐには理解できないんですが……たとえば $a < x < b$ で連続とか」

僕「うん。連続や微分可能のような条件はあとで考えるとして、 一番大きな主張のところを先に話すよ。つまり、 $$ \frac{f(b) - f(a)}{b - a} = f'(c) $$ を満たす実数 $c$ が、 $a$ と $b$ のあいだに存在するというところ。 まず左辺の式、 $$ \FBOX{\frac{f(b) - f(a)}{b - a}} = f'(c) $$ はさっきから言ってる《平均の変化率》を表している」

テトラ「はい」

僕「イメージはわかるよね。 $y = f(x)$ のグラフで $a \LEQ x \LEQ b$ の範囲をいまは考えているんだけど」

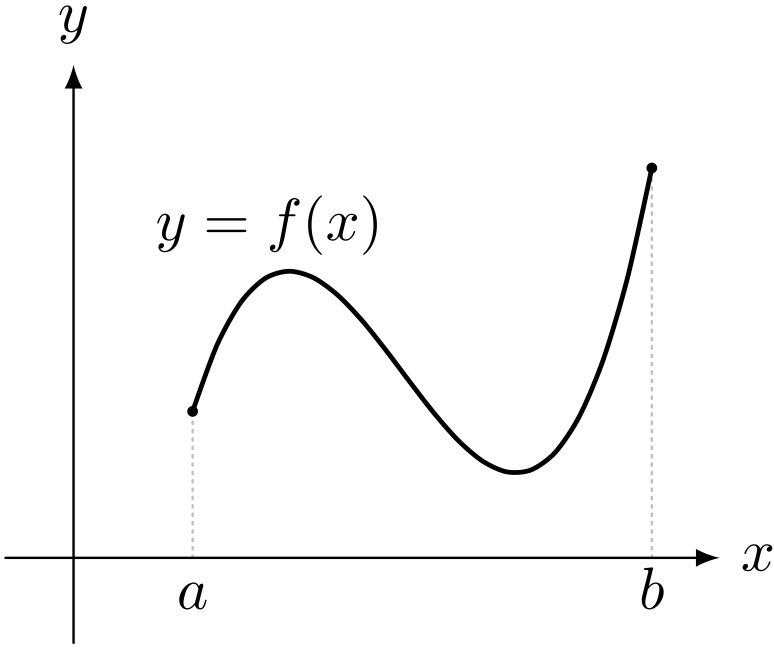
テトラ「大丈夫です！」

僕「《平均の変化率》というのは、 $y = f(x)$ のグラフの上の二点 $(a,f(a))$ と、 $(b,f(b))$ を結ぶ《線分の傾き》になるよね」

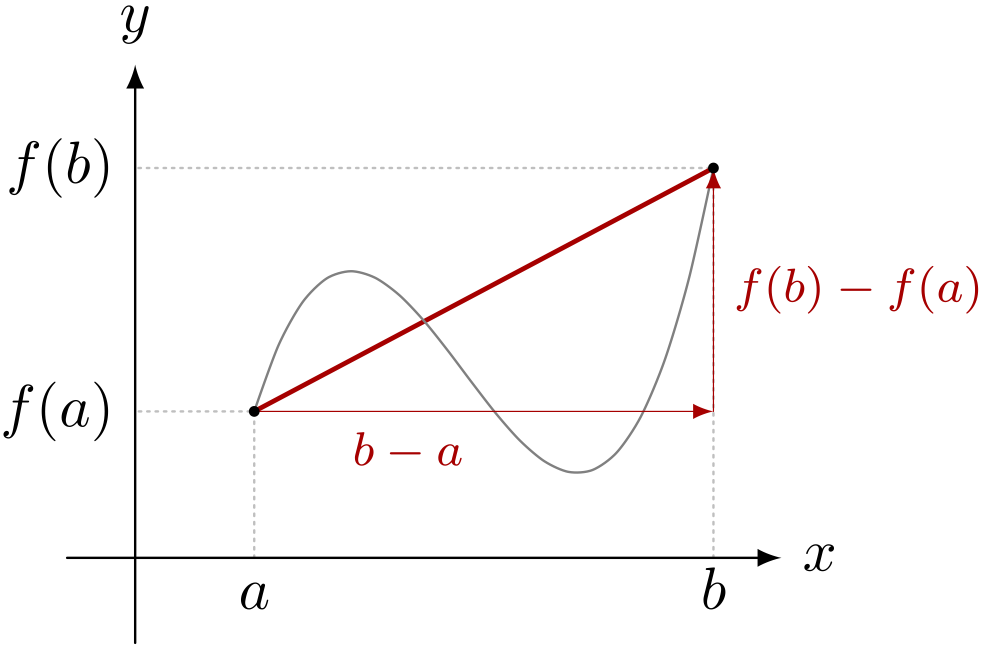
テトラ「はい、そうですね」

僕「それに対して、 $$ \frac{f(b) - f(a)}{b - a} = \FBOX{f'(c)} $$ の右辺の式は関数 $f(x)$ を微分して得られる導関数 $f'(x)$ で $x = c$ にしたときの値という意味だね。 $f'(c)$ は、 $x = c$ での $f(x)$ の微分係数と呼んでもいいし、 $y = f(x)$ のグラフを考えたとき、 $x = c$ での《接線の傾き》と呼んでもいい」

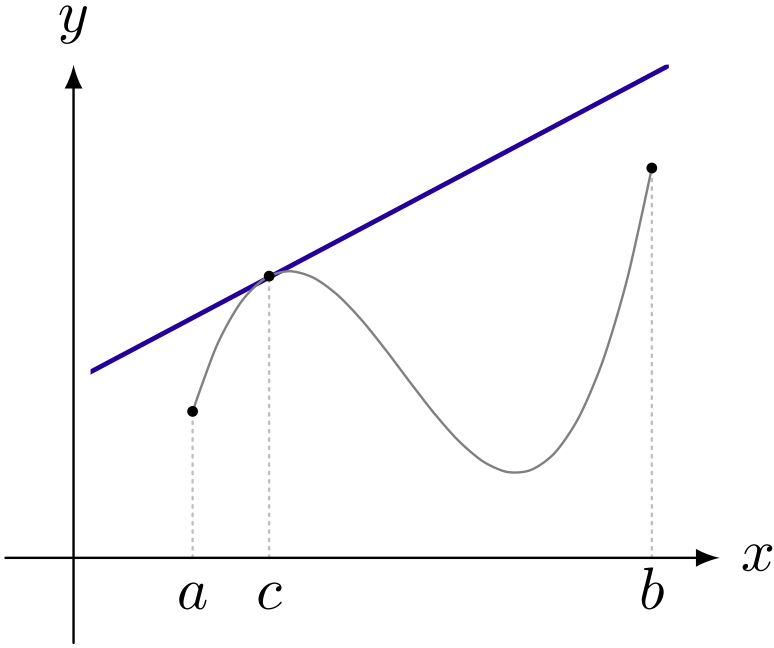
テトラ「……はい」

僕「そこまで式を理解していれば、平均値の定理の主張はもうわかるよ。 $$ \frac{f(b) - f(a)}{b - a} = f'(c) $$ を満たす実数 $c$ が、 $a$ と $b$ のあいだに存在するというのはどういうことかというと…… 《線分の傾き》と《接線の傾き》が等しくなるところが $a$ から $b$ までのあいだにあるということ。 傾きが等しいということは、こんなふうに平行になる接線が存在するという意味だね」

テトラ「……！」

僕「こんなふうに考えてもいいよ。 $x$ の値が $a$ から $b$ まで変化していくとき、関数 $f(x)$ の値は $f(a)$ から $f(b)$ まで変化する。 その途中では大きく増加したり、小さく増加したり、ときには減少したりするかもしれない。 つまり途中での《瞬間の変化率》は一定とは限らない。 でも途中のどこかでは《瞬間の変化率》が《平均の変化率》と等しくなるところが必ずある」

あたりまえだからわからない

テトラ「ちょ、ちょっとお待ちください。 こういうことでいいんでしょうか。 $y = f(x)$ のグラフを考えると、 両端を結んだ線分と平行な接線が必ずある？　そういうことですか？」

僕「そうだね。 連続であるという条件はグラフが途切れずにずっとつながっている保証のためにあるし、 微分可能であるという条件は必ず途中に接線が引けるという保証のためにある」

テトラ「あのう……すみません、あたしには、この定理は《あたりまえ》のように見えるんですが」

僕「まあ、そうだね」

テトラ「だってそうですよ。 いろんな接点を想像して、そこの接線を考えてみると、大きく傾いたり小さく傾いたりしますけど、 途中ではどこかで平行になります……必ず平行になりそうですっ！」

僕「うん、テトラちゃんのその直観はまちがってはいないと思うよ。 僕もこの平均値の定理の話を聞いたときは《あたりまえ》って思ったし」

テトラ「このような《あたりまえ》の定理に名前が付いているのが不思議です……」

僕「ところが平均値の定理は、入試の過去問でもときどき出てくることがあるんだよ」

テトラ「へええっ！　 このように《あたりまえ》のこと、どんなふうに問題になるんですか？」

僕「過去問で出てくるというか、問題を解くときにとても便利に使えるというか」

テトラ「想像できません……」

僕「ちょっといま複雑な問題は思い出せないから簡単な例だけど、こんなのはどうかなあ」

テトラ「ははあ……」