![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
後輩のテトラちゃんと僕は関数についておしゃべりをしている(第203回参照)。
僕「最大値や最小値を考えることを 《関数の特徴を捕らえる》と表現するのもいいけど、 《関数とお友達になる》って表現も何だかいいよね」
テトラ「き、恐縮です。 子供っぽい言い方で恥ずかしいんですが……つい、 そういうふうに考えてしまうんです」
僕「そんなことないと思うよ。 特徴を捕らえるにせよ、 お友達になるにせよ、次に来るのは《仲間探し》かもしれないね」
テトラ「仲間探しといいますと……パーティ組むみたいに?」
僕「ほら、友達だったら《同じ中学校だった》とか、 《あの人とこの人はバスケ部》みたいに考えるよね」
テトラ「そうですね。《同じ髪形》とか」
僕「関数でも《仲間探し》ができそうだなって思ったんだ。 つまり、同じ特徴を持った関数を探してみよう!ということ」
テトラ「なるほど……たとえば《最大値が $1$ になる関数さんは集まりなさい!》のように?」
最大値が $1$ になる関数たち
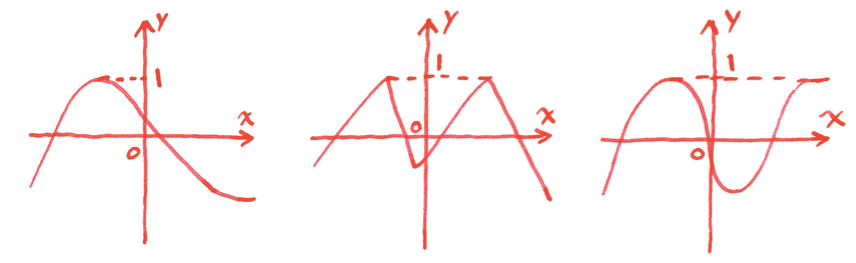
僕「うん、そういう感じ。 まあ、僕はそこまで具体的には考えなかったけど。 最大値が $1$ になる関数よりも前に、 そもそも最大値が存在するかどうかという大きな特徴もあるから」
テトラ「ああ……」
僕「たとえば、話を簡単にするために、定義域と終域のどちらも実数全体だと決めておくことにすると、 最大値が存在するかどうかで関数を二つに分類できるよね(第203回参照)?」
テトラ「そうですね。たとえば、関数 $2x + 3$ には最大値は存在しません。 $x$ を大きくすれば、 $2x + 3$ の値はいくらでも大きくできるからです……そういうお話ですよね?」
僕「そうだね。いまテトラちゃんが言った関数 $2x + 3$ には最小値も存在しないね」
関数 $2x + 3$ には最大値も最小値も存在しない
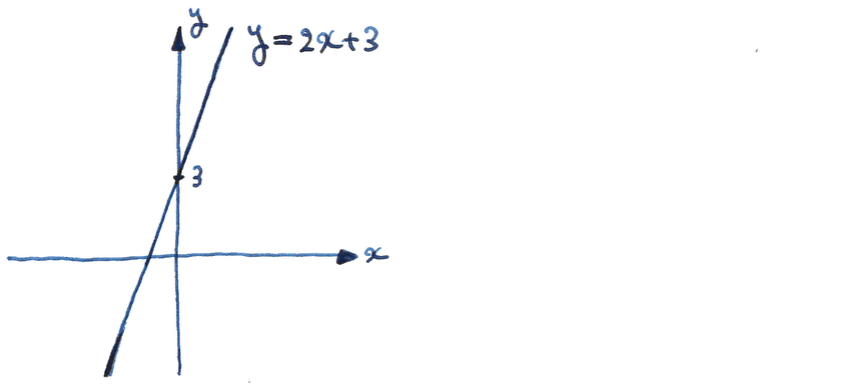
テトラ「はい」
僕「じゃ、最大値が存在する関数の例は?」
テトラ「それは、さっきも出てきた放物線……二次関数がそうです(第203回参照)」
僕「具体的には?」
テトラ「たとえば、関数 $x^2$ だと……あ、これはだめですね。これには最小値はありますが、最大値はありません。 上下を逆にして関数 $-x^2$ ならいいですね。これだと最大値として $0$ をとることができます」
関数 $x^2$ には最小値はあるが、最大値はない
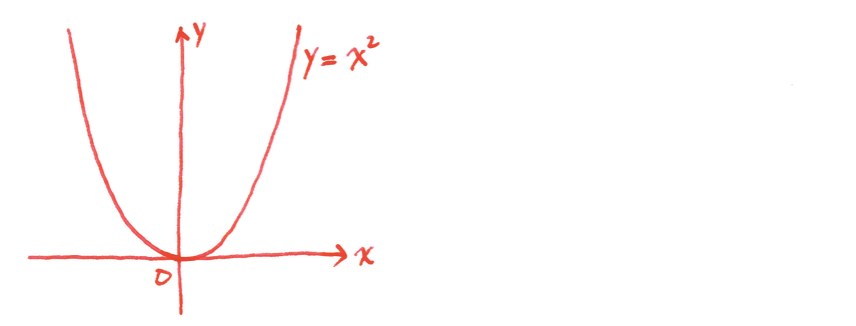
関数 $-x^2$ には最小値はないが、最大値はある

僕「そうそう、そうなるね。一般に $x$ の冪乗になっている関数は、奇数乗か偶数乗かで分類ができる。 $n = 1,2,3,\ldots$ としたとき……」
テトラ「はい。たとえば、関数 $x^3$ は奇数乗で、最小値も最大値のどちらもありません」
関数 $x^3$ には最小値も最大値もない

僕「そうだね。じゃ、今度は最大値と最小値の両方がある関数の例は見つけられる?」
テトラ「最大値と最小値の両方がある関数……あっ、それも先ほど出てきました。 たとえば関数 $\sin x$ ですね。 だって、 $-1 \leqq \sin x \leqq 1$ が成り立ちますから、最大値と最小値の両方があります」
関数 $\sin x$ には最大値と最小値の両方がある
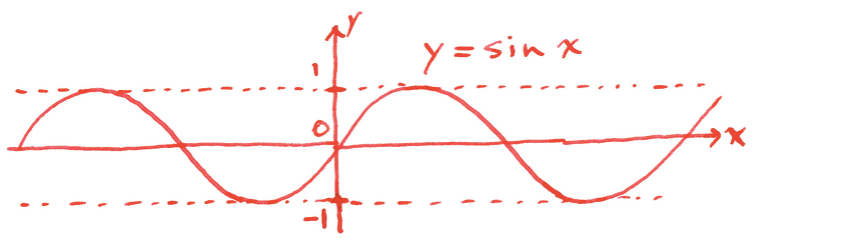
僕「そうだね。それで正解。 ただ、テトラちゃんはいま 『$-1 \leqq \sin x \leqq 1$ だから最大値と最小値がある』と説明したけど、 これはちょっぴり言葉不足だよ」
テトラ「言葉不足……といいますと」
僕「グラフも描いているからテトラちゃんはわかっているはずだけど、 どんな実数 $x$ に対しても 『$-1 \leqq \sin x \leqq 1$ が成り立つ』のように不等式を書くだけじゃなくて、 $\sin x = -1$ になる実数 $x$ が存在するし、 $\sin x = 1$ になる実数 $x$ も存在する、といわなくちゃ。 不等式が出てきたときには等号成立を意識しないと」
テトラ「ははあ……確かに」
僕「不等式を書くだけじゃよくないと思ったのはね、 $\sin x$ の値を考えてみると、どんな実数 $x$ に対しても、 $$ -123 \leqq \sin x \leqq 456 $$ という不等式だって成り立っているから。 $\sin x$ の値はぜったいに $-123$ 以上だし、 $456$ 以下だよね。 でも、 $\sin x$ の最小値は $-123$ じゃないし、最大値は $456$ じゃない」
テトラ「はい、先輩のおっしゃることはよくわかります。テトラはうっかりしていました。等号が成立するか気を付けよですね」
僕「でも、テトラちゃんがいうように $\sin x$ には最大値も最小値も存在するのは確かだよ。 最大値は $1$ で、最小値は $-1$ だよね」
テトラ「……」
僕「どうしたの?」
テトラ「はい……あのですね。先ほど考えた関数、 たとえば $x^3$ は最大値も最小値も存在しません。 それに対して、 $\sin x$ は最大値も最小値も存在します。 $y = x^3$ や $y = \sin x$ のグラフを描けば、確かに両方の関数は違うとわかるんですが、 最大値と最小値の存在を考えるだけでも、 確かに違うといえるわけですね……そんな、 あたりまえのことで感心していました」
僕「うんうん。特徴を捕らえるってそういうことだからね」
テトラ「《関数とお友達になる》としたら、いろんなことを知ってたほうがいいですね。 『あなたのこと、もっと教えてくださいな』って聞くみたいに」
僕「質問すると、関数によって答えは違うわけだね」
テトラ「はい。関数 $x^3$ の値はいくらでも大きくなりますし、いくらでも小さくなります。 でも、関数 $\sin x$ の値はそうじゃありません。 ふにゃふにゃと波打ってはいますが、 $-1$ 以上 $1$ 以下の範囲に収まっています。 あっ、これって二つの関数の値域を比べているということですね?」
僕「うん、その通りなんだけど、テトラちゃんの言葉は少し気になるよ」
テトラ「あっ、また《ふにゃふにゃ》だなんて、子供っぽい言い方をしちゃいましたっ!」
僕「いやいや、そっちじゃなくて。あのね、いまテトラちゃんは関数 $x^3$ の値は、 《いくらでも大きくなるし、いくらでも小さくなる》って言ったけど、 それはどういう意味で言ったの?」
テトラ「え、ええと…… $x^3$ の値はいくらでも大きくすることができますし、 いくらでも小さくすることができます。 そう言ったのは、定義域を実数全体で考えているからです。 $x$ の値はいくらでも大きな実数にできますから、 $x^3$ の値はいくらでも大きな実数にできます。 そして、マイナスにすれば、いくらでも小さな実数にできます……あっ、 言い換えるなら、関数 $x^3$ の値域は実数全体になります……そうですよね?」
僕「うん、それは正しいよ。定義域を実数全体で考えるなら、 関数 $x^3$ の値域は実数全体になる。そう表現すれば正確に考えが伝わるね」
テトラ「す、すみません……あたしには、先輩が何を気になさっているのか、 まだわかっていないようです」
僕「あ、ごめんね。僕は《いくらでも大きくなる》や《いくらでも小さくなる》という言葉は、 考えようによってはあいまいで誤解を生むかも、と思ったんだよ」
テトラ「そうなんですか……あたしは、グラフを想像しながら話していたので、 誤解を生むかどうかはわからないんですが」
僕「たとえば、関数 $e^x$ を考えてみたらわかるよ。定義域はさっきと同じく実数全体とする。 そのとき、指数関数 $e^x$ には最大値と最小値は存在するだろうか?」
クイズ(指数関数)
定義域を実数全体とする。
関数 $e^x$ には最大値は存在するか。また最小値は存在するか。

テトラ「$y = e^x$ のグラフはこういうものですよね?」
指数関数 $y = e^x$ のグラフ

僕「そうだね」
テトラ「最大値は存在しませんよね。だって《いくらでも大きく》なりますから」
僕「じゃ、最小値は?」
テトラ「最小値は $0$ じゃ……ないですよね? 最小値は存在しない?」
僕「うん、そう。そうなんだ。指数関数 $e^x$ には最小値は存在しない。最大値も最小値も存在しないね」
クイズの答え(指数関数)
定義域を実数全体とする。
関数 $e^x$ には最大値は存在しないし、最小値も存在しない。
テトラ「えっと、関数 $x^3$ と $e^x$ はどちらも最小値はないですけれど……比べてみると、 何となく、先ほど先輩がおっしゃったことがわかったように思います。 とても小さい値を持つ $x$ を考えたとします。たとえば $x = -10000$ のように。 そうすると、 $e^x$ の値はとても $0$ に近くなりますが、 $0$ にはなりません」
僕「うん、そうだね。それで?」
テトラ「それで、 $x$ の値として、もっと小さなものを選んだとすれば、 $e^x$ の値はもっと $0$ に近づきます。 でも $0$ にはなりません。 $e^x$ の値はぜったいに $0$ にはなりません。でも……でも、 $x$ の値を小さくすればするほど、 $e^x$ の値は小さくなっていきます」
僕「うんうん」
テトラ「もうこれ以上 $e^x$ の値を小さくすることはできない! なんてことは起きません。 $e^x$ がすごく小さくなっても、 $x$ の値をもっと小さくすれば $e^x$ の値はもっと小さくできます」
僕「ということは《いくらでも小さく》できる?」
テトラ「ううう……先輩はこういう《あいまいさ》を気になさっていたのですか……《関数 $x^3$ の値はいくらでも小さくできる》と、 《関数 $e^x$ の値はいくらでも小さくできる》というのはずいぶん違う状況ですね」
僕「うん。その二つの状況をちゃんと区別すると、こう整理できるかな。 定義域と終域のどちらも実数全体であるような関数 $f$ を考えたとして……」
関数 $f$ の値は《いくらでも小さくなる》とは?
テトラ「……」
僕「グラフで描くとこうなるね」
【状況1】どんな実数 $m$ に対しても、 $f(a) < m$ となるような実数 $a$ が存在する
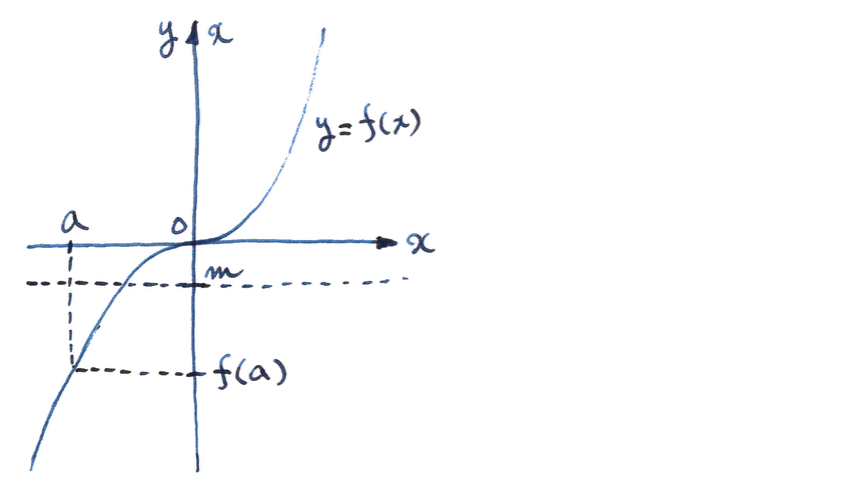
【状況2】どんな実数 $b$ に対しても、 $f(c) < f(b)$ となるような実数 $c$ が存在する

テトラ「なるほどなるほどなるほど! 関数 $x^3$ は【状況1】で、関数 $e^x$ は【状況2】ですねっ!!」
僕「もちろん、 《いくらでも小さくなる》や《いくらでも小さくできる》という表現が何を意味しているか、 ちゃんと相手とわかりあっているなら問題はないんだよ。誤解しなければ何も問題はない。 でも、相手に正確に伝えたいときには注意しないとね」
テトラ「はい。先ほど先輩が整理してくださったのでわかりました。 《いくらでも》というのが、 何と比較しているのか不明確になるときはあぶないですね」
僕「そうだね。いまは終域を実数全体で考えているから、 【状況1】の方は終域の要素 $m$ と比較しているし、 【状況2】の方は値域の要素 $f(b)$ と比較しているという違いがあるわけだ」
テトラ「なるほどっ!」
僕「定義域が実数全体のとき、関数 $x^3$ の値域は実数全体の集合だね。 そして関数 $e^x$ の値域は……」
テトラ「ちょっとお待ちください。テトラが答えます。 関数 $e^x$ の値域は $0$ より大きい実数全体の集合ですね?」
僕「そういうことになるね。そして、関数 $e^x$ には最大値も最小値も存在しない」
テトラ「……関数 $e^x$ には、最大値も、最小値も存在しない……」
僕「あれ、テトラちゃんは、理解しているよね?」
テトラ「はい。はいはい。理解しています……あのですね。 関数 $e^x$ で《最大値が存在しない》というのは、 先ほどの【状況1】と似ています。不等号は逆向きですけれど。 つまり、どんな実数 $m$ に対しても、 $e^a > m$ という実数 $a$ があるということです。 でも《最小値が存在しない》というのは【状況2】です。 つまり、どんな実数 $b$ に対しても、 $e^c < e^b$ という実数 $c$ があるということ……ですね。 同じ《存在しない》でも、状況が違うんだなあ……と思ったんです」
僕「なるほど、そうだね。存在しないという点は同じだけど、 有界(ゆうかい)かどうかの点が違うと表現できるね。 関数 $e^x$ の値域は $0$ より大きい実数全体の集合になる。 下に有界だけど、上に有界じゃない」
テトラ「なるほど……《有界》という表現があるんですね」
テトラちゃんはさっとノートにメモをとる。
テトラ「先輩と関数のお話をしてきて、 定義域、終域、それから値域について、 だいぶわかって……だいぶ慣れてきたみたいです」
僕「それはよかった。 テトラちゃんは終域のことを気にしていたからね」
テトラ「はい……関数を定義しているとき、 定義域の方は一つ残らず使うのに、 終域の方は余ってもいいというのが変だなと感じたんです。 でも、きっちり使い尽くす値域という言葉があると知って納得です」
僕「終域と値域が一致する関数があってもいいんだよ、 もちろん」
テトラ「はい、それはわかります。 たとえばさっきの関数 $x^3$ もそうですよね。 定義域と終域をどちらも実数全体として考えたとき、 値域は終域に一致します。 $x^3$ はどんな実数の値でも取ることができますから」
僕「うん。 そういう《終域と値域が一致する関数》のことを全射(ぜんしゃ) っていうんだよ」
テトラ「ああ……それは以前お聞きしたことがあります(『数学ガールの秘密ノート/場合の数』参照)。 全射と単射と全単射。こういう図で覚えています」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2017年8月25日)