![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ここは僕の部屋。僕とユーリはオイラーの関数 $\varphi(n)$ についておしゃべりをしている(第199回参照)。
僕「$\varphi(n)$ について、こんな問題を考えることができるわけだよ!」
オイラーの関数 $\varphi(n)$
オイラーの関数 $\varphi(n)$ は、 $1,2,3,\ldots,n$ のうち、 $n$ と互いに素な整数の個数を表す。
もしも、 $p,q$ が素数で $p < q$ として、 $n = pq$ が成り立つ場合には、 $$ \varphi(n) = \varphi(pq) = (p-1)(q-1) $$ がいえる。
それでは、 $n = pq$ と表せないときも含めて考えると、 $$ \varphi(n) $$ はどんな式で表すことができるだろうか。
ユーリ「うわー、めんどくさそー……んにゃ、わかった。 数えればいーんじゃん。だって $\varphi(n)$ は《$1,2,3,\ldots,n$ で $n$ と互いに素な整数の個数》なんだから、 $1$ から $n$ まで調べて数えていけば……やっぱめんどい?」
僕「《$1,2,3,\ldots,n$ で $n$ と互いに素な整数の個数》だから、 いいかえると《$1,2,3,\ldots,n$ で、 $n$ との最大公約数が $1$ になっている整数の個数》を調べればいいよね。 《互いに素》は《最大公約数が $1$》という意味だから。 $n$ が小さいうちはめんどうじゃないよ」
ユーリ「$\varphi(1) = 1$ でしょ?」
僕「そうだね。 $1$ と互いに素なのは $1$ という $1$ 個だけ」
$$ \begin{array}{c|cccccc} n & 1 & \cdots \\ \hline \varphi(n) & 1 & \cdots \\ \end{array} $$ユーリ「$n$ が素数のときは、 $n-1$ になるんだよね?」
僕「そうそう。素数の定義を考えればそうなる。 $n$ が素数だったら、 $1$ から $n$ までのうちで $n$ の約数は $1$ と $n$ しかない。 ということは、 $1,2,3,\ldots,n-1$ のどれを選んでも $n$ との公約数は $1$ しかない。公約数が $1$ しかないんだから、 最大公約数も $1$ しかない」
ユーリ「$\varphi(n)$ の表で $n$ が素数のところはすぐわかる!」
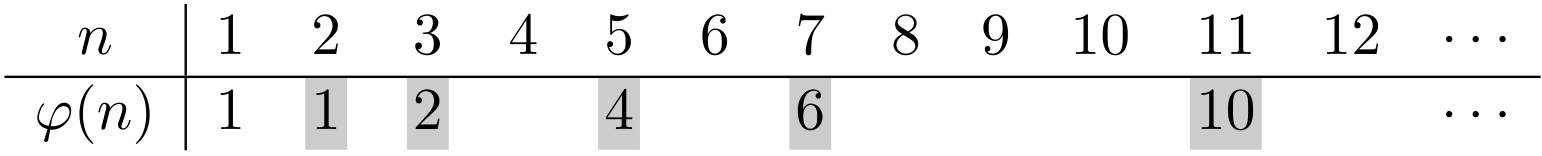
僕「それから、さっきの $\varphi(pq) = (p-1)(q-1)$ を使えば、 二素数の積になっている場合もすぐわかる」
ユーリ「そだね。 $6 = 2\cdot3$ とか、 $10=2\cdot5$ とか……」

僕「$\varphi(4)$ は数えればすぐにわかる」
ユーリ「$4$ と互いに素なのは、 $1$ と $3$ だけだよね。 だから $2$ 個で、 $\varphi(4) = 2$」
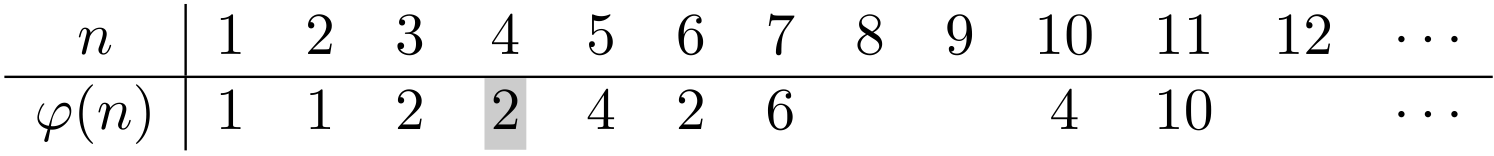
僕「$\varphi(8)$ は……」
ユーリ「$1$ は互いに素、 $2$ は違う。 $3$ は互いに素、 $4$ は違う……あ、これ、奇数かどうか調べればいーんじゃない?」
僕「表にしてみようよ」
$1,2,3,\ldots,8$ のうち、 $8$ と互いに素になるものはどれか
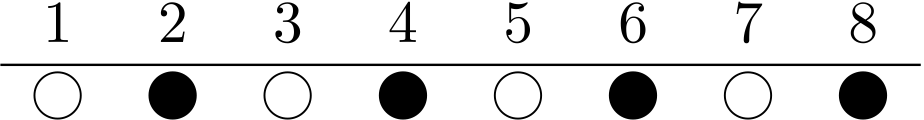
$8$ と互いに素なら $\SO$ で、互いに素じゃないなら $\NO$ とした。
ユーリ「うん、だから、 $\varphi(8) = 4$ ってことでしょ。次は $\varphi(9)$ だね!」
僕「ちょっと待って、ユーリ。先に進む前に考えようよ」
ユーリ「何を?」
僕「《例示は理解の試金石》だから、 具体的な $n$ で $\varphi(n)$ の例を作るのは大事だけど、 例をどんどん作っていくだけじゃつまらないよ。 具体例をもとにして一般的に考えなくちゃ」
ユーリ「出たな一般化」
僕「$\varphi(8) = 4$ を求めたけど、 $n = 8$ からどうやって $\varphi(8) = 4$ がわかったんだろう」
ユーリ「$8$ と互いに素なのは奇数だから」
僕「うん、そうだね。そして $1,2,3,\ldots,8$ の中で奇数は $4$ 個だから $\varphi(8) = 4$ になった。 じゃあ、 $8$ と互いに素なのは奇数ってどうしてわかったんだろう」
ユーリ「試したから」
僕「……」
ユーリ「だって、 偶数だったら $8$ との公約数は $2$ とか $4$ とかになっちゃうから、 互いに素になんないでしょ?」
僕「そうだね。 その《偶数だったら》というユーリのアイディアはどこから来たんだろう」
ユーリ「試したから。試したから……うん、そっか! 素因数分解だ! $8 = 2^3$ だよね。だから、 $2$ があるのはだめなんだね!」
僕「うん、その通り。 $8$ は、 $8 = 2^3$ と素因数分解できる。 だから、 $8$ は《$2$ という素因数》を持つことがわかる。 ということは、 $1,2,3,\ldots,8$ のうち、 $2$ という素因数を持っている整数は、 $8$ と互いに素にはなれない。 $2$ 以上の公約数が作れてしまうから」
ユーリ「そだね。ユーリもそー言いたかったの」
僕「素因数分解は強力だよ……」
そうなんだ。素因数分解は強力だ。整数の構造を明らかにしてくれる。 僕はそのことをきっと忘れない。 だって……(『数学ガール/フェルマーの最終定理』参照)。
ユーリ「お兄ちゃん?」
僕「あ、うん。素因数分解を使えば、 $\varphi(n)$ を求める大きなヒントが得られそうだよ」
ユーリ「$n$ が偶数だったら、 $1,2,3,\ldots,n$ のうち偶数のものは、 $n$ と互いに素になれない?」
僕「うん、それは正しいけど、それだけだと弱い。 だって、 $n$ が偶数のとき、 $1,2,3,\ldots,n$ のうち奇数だからといって、 $n$ と互いに素とは限らないし」
ユーリ「えっ? 何いってるですか?」
僕「$n = 6$ という偶数のとき、 $3$ は奇数だけど、 $6$ と $3$ は互いに素じゃないよね?」
ユーリ「あー……」
僕「さっきの $n = 8$ では $8$ は素因数に $2$ しかなかった。 $$ 8 = 2^3 = 2\times2\times2 $$ だから、 $1,2,3,\ldots,8$ のうち、 奇数は $8$ と互いに素で、偶数は $8$ と互いに素じゃないといえたんだ」
ユーリ「あー……ちょっとしゃべるのやめて。わかったから、わかったから!」
ユーリは、僕の話を制して、しばらく表を見ていた。
$1,2,3,\ldots,8$ のうち、 $8$ と互いに素になるものはどれか
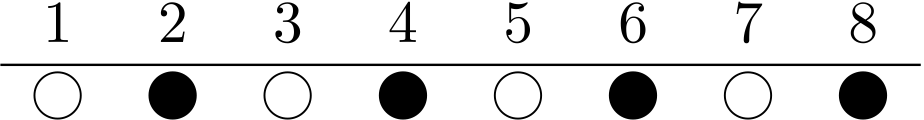
$8$ と互いに素なら $\SO$ で、互いに素じゃないなら $\NO$ とした。
僕「……」
ユーリ「……あのね、こうなる! $p$ を素数とするじゃん? そして、 $n$ が $p$ の……何ていうの?」
僕「冪乗(べきじょう)のことかな。累乗(るいじょう)ともいうけど。 $p^j$ の形になった数のことだろ?」
ユーリ「すごい! お兄ちゃんテレパシーだ!」
僕「超能力者だから」
ユーリ「それはさておき。 $n$ が素数 $p$ の冪乗だとするじゃん? $n = p^j$ とか。そのとき、 $\varphi(n)$ は $p^{j-1}(p-1)$ になるんじゃない?」
僕「おお、いきなりの一般化だなあ。ユーリがいうのは、 $p$ が素数で、 $j$ が $1$ 以上の整数のとき、 $$ \varphi(p^j) = p^{j-1}(p-1) $$ ということだね?」
ユーリ「そーそー!」
僕「$8$ で検算すると、 $8 = 2^3$ だから、 $p = 2, j = 3$ ということ。すると、 $$ p^{j-1}(p-1) = 2^{3-1}(2-1) = 4 $$ そして実際 $\varphi(8) = 4$ になってる。いいね!」
ユーリ「それにね、それにね、 $j = 1$ のとき! $p^0$ って $1$ でしょ? だから、 $$ p^{j-1}(p-1) = p^{0}(p-1) = p-1 $$ になるけど、ちゃーんと、 $p$ が素数のとき、 $\varphi(p) = p-1$ になってるんだよ!」
僕「すごい! うまいな……ところで、ユーリは、 $$ \varphi(p^j) = p^{j-1}(p-1) $$ が成り立つことを証明できる?」
ユーリ「できるよん。だって、 $p^j$ までで $p-1$ を何回繰り返せるかを考えればわかるでしょ?」
僕「うん、そうだね。僕にはユーリが何を考えてそういってるかはわかる。 でもそれだと証明とはいえないなあ」
ユーリ「じゃ、どーすればいーの?」
僕「うん、まずは、証明したい命題を書いてみようか。これがユーリの証明したいこと」
命題(素数の冪乗とオイラー関数)
$p$ を素数とし、 $j$ を $1$ 以上の整数とする。このとき、 $$ \varphi(p^j) = p^{j-1}(p-1) $$ が成り立つ。
ユーリ「ふんふん」
僕「証明は、こんな感じかなあ」
証明(素数の冪乗とオイラー関数)
$p^j$ の素因数は $p$ だけなので、 「整数が $p$ の倍数ではないこと」と 「整数が $p^j$ と互いに素であること」とは同値である。
《$1,2,3,\ldots,p^j$》という $p^j$ 個の整数のうち、《$p$ の倍数になるもの》は $p^{j-1}$ 個ある。 《$p$ の倍数にならないもの》は、 $$ p^j - p^{j-1} $$ 個ある。
したがって、 $$ \varphi(p^j) = p^j - p^{j-1} = p^{j-1}(p - 1) $$ がいえる。 (証明終わり)
ユーリ「うわーめんどい……けど、 これ、ユーリが考えていたのと同じことかも」
僕「ユーリはどんなふうに考えたの?」
ユーリ「さっきのこれでわかったの」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2017年6月30日)