第199回 シーズン20 エピソード9

からみあう素数（前編）

僕の部屋

ユーリ「だから、この数式の意味を教えてよー！　早く早く！」

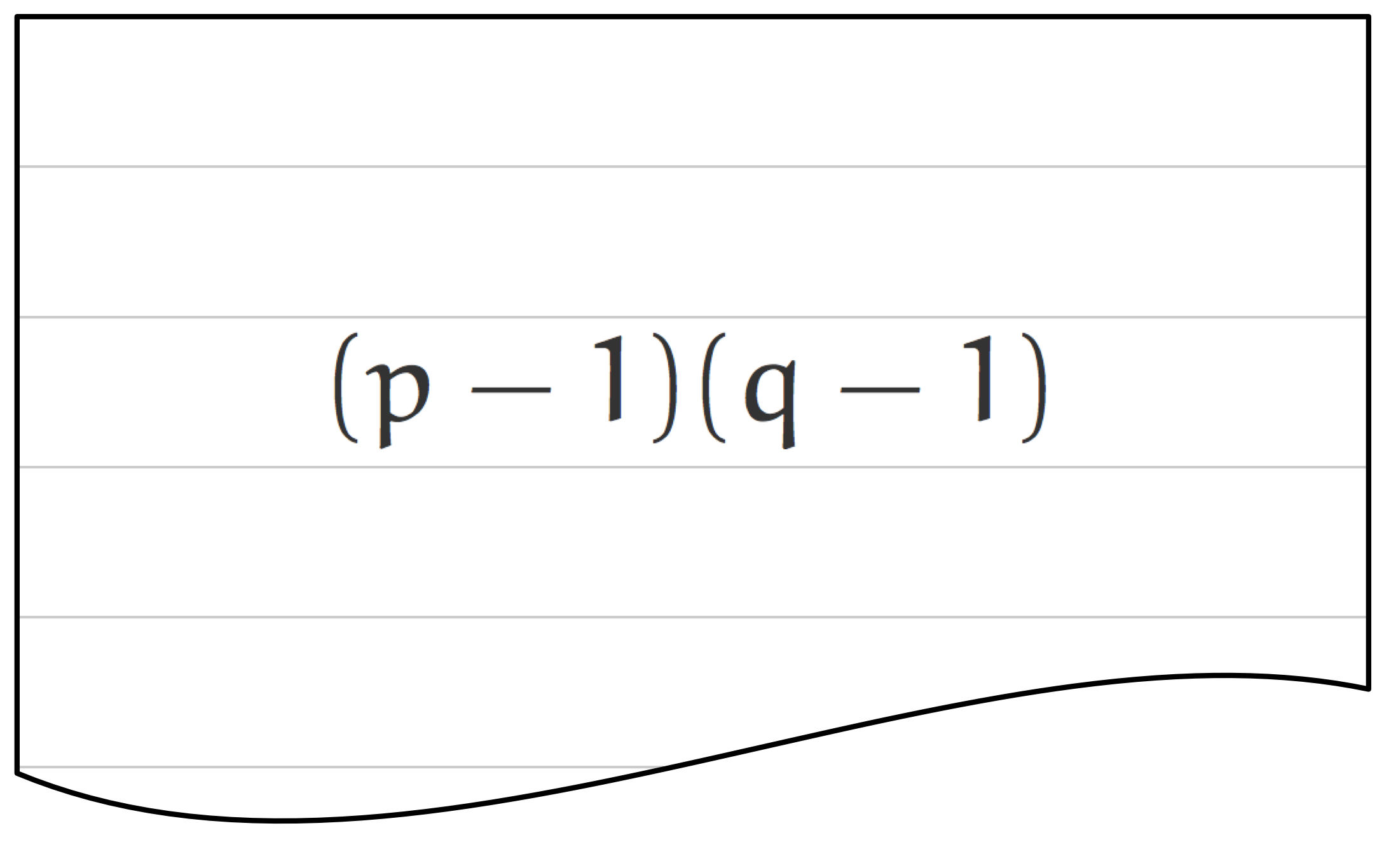
僕「$(p-1)(q-1)$ という数式の意味？　 $p-1$ と $q-1$ の積だよ」

ユーリ「そーゆーんじゃなくて、 もっとカッコイイ意味があるんでしょ？」

僕「そもそも、この数式はどこからやってきたの？」

ユーリ「えっとね。《とある知人》から」

僕「《とある知人》というボーイフレンドね。はいはい」

ユーリ「センサクはいいから。 $(p-1)(q-1)$ の意味は？　さーさー！」

僕「$p$ や $q$ に何か条件があるんじゃないの？」

ユーリ「そーだった。 $p$ と $q$ は素数で $p < q$ だって」

僕「へえ。ということは、話を整理すると、こういう研究クイズ？」

ユーリ「研究クイズ？」

僕「そういうことだろ？　クイズなんだから、 恐らく《彼氏》が想定している答えはある。 でも、解くべき問題は明確じゃないから、 自由に研究してかまわない。何かおもしろい性質を見つけてみよう……と、 そういうことなんじゃないの？　自由に研究するクイズ。研究クイズ」

ユーリ「《あいつ》は《彼氏》とかじゃないし……」

僕「ユーリはどんなふうに考えたんだろう」

ユーリ「うーん……偶数になるのはすぐわかったけど、 そっから先はおもしろい性質なんてわかんなかった」

僕「こういうものを研究するときには、小さい数で試すのが大事だよね」

ユーリ「ふんふん。プロの選ぶ王道ですか」

小さな数で試す

僕「$p$ と $q$ は素数で、 $p < q$ が成り立っている。 そのときに $(p-1)(q-1)$ を調べてみる。小さな数でね」

ユーリ「小さな数って、たとえば、 $p = 2$ で $q = 3$ ということでしょ？」

僕「そういうことだね。素数は、自分自身と $1$ 以外に約数を持たない $2$ 以上の整数。 具体的には $2,3,5,7,11,13,17,19,\ldots$ だから、 この中から異なる二つの数を選べばいい。二つのうち小さい方を $p$ にして、 大きい方を $q$ にすれば $p < q$ という条件は満たせることになるね」

ユーリ「カンタンだよ！　 $(p-1)(q-1) = 2$ でしょ」

僕「そうだね。他の場合も考えてみよう。 たとえば……」

ユーリ「たとえば、 $p = 2$ で $q = 5$ のとき！」

僕「あたりまえだけど、 $p = 2$ のときは、 $(p-1)(q-1) = q - 1$ になるね」

ユーリ「そだね。必ず偶数になる」

僕「うん。 素数の中で偶数なのは $2$ だけ。 $2$ 以外の素数はすべて奇数になる。 $p < q$ だから、 $q$ は絶対に奇数。 だから $q - 1$ は絶対に偶数になる。つまり $p = 2$ のとき、 $(p-1)(q-1)$ は偶数になるよ」

ユーリ「$q-1$ は絶対に偶数になるんだから、 $p$ が $2$ じゃなくても $(p-1)(q-1)$ は絶対に偶数だよ」

僕「そうだね。その通り」

ユーリ「こんなのはすぐわかるもん。 そーじゃなくて、もっとすごい性質ないの？」

僕「うん。 $(p,q) = (2,3)$ と $(p,q) = (2,5)$ の場合を調べたけれど、 もっと調べてみよう。そのために、こういう関数 $f$ を定義しよう」

ユーリ「へ？」

僕「こうすれば、僕たちが具体的な数で試すときに書きやすいからね。 調べたことを、 $$ f(2,3) = 2 $$ や、 $$ f(2,5) = 4 $$ のように簡潔に書くことができる」

ユーリ「ほほー」

僕「もっと一般的に、こんな書き方もできるわけだ」

ユーリ「なるほどね」

僕「……」

ユーリ「……何かわかった？」

僕「いや、わからないなあ。強いていえば……うん、 $f(p,q)$ の値は、 $(p,q) = (2,3)$ を除けば素数にならない」

ユーリ「そりゃそーですなー。 $f(p,q)$ は偶数で、偶数の素数 $2$ になるのは、 $f(2,3)$ だけだもん」

僕「そもそも $p-1$ と $q-1$ の積になってるんだから、 $p-1$ が $1$ になる場合に注意すれば、素数じゃないというのはすぐわかる。 ……そうか、 $p,q$ という二つの素数が出てくるんだから、 さっきのような一次元の表じゃなくて、二次元の表にすべきなんだな」

ユーリ「ほほー……で？」

僕「うーん……特に何かがわかるわけでもないか」

ユーリ「ねーお兄ちゃん、ユーリ気づいたことあるんだけど」

僕「何か発見した？」

ユーリ「んにゃ。いまお兄ちゃん『二次元の表にすべき』っていったじゃん？　そーじゃなくても、二次元だよね？」

僕「どういう意味？」

ユーリ「$(p-1)(q-1)$ っていう掛け算なんだから、縦が $p-1$ で横が $q-1$ の長方形の面積みたいな」

僕「なるほど！　確かに！　たとえば、 $p = 3, q = 5$ なら、こういう意味？」

ユーリ「そーそー。 $f(3,5) = 8$ ってゆーのは、 長方形の中に置いた白丸の個数でしょ？　そこに何か深ーいイミが隠されてる？」

僕「うーん……どうだろう」

ユーリ「あんまり、関係なかった？」

僕「掛け算を作ってみればいいのかな……違うか」

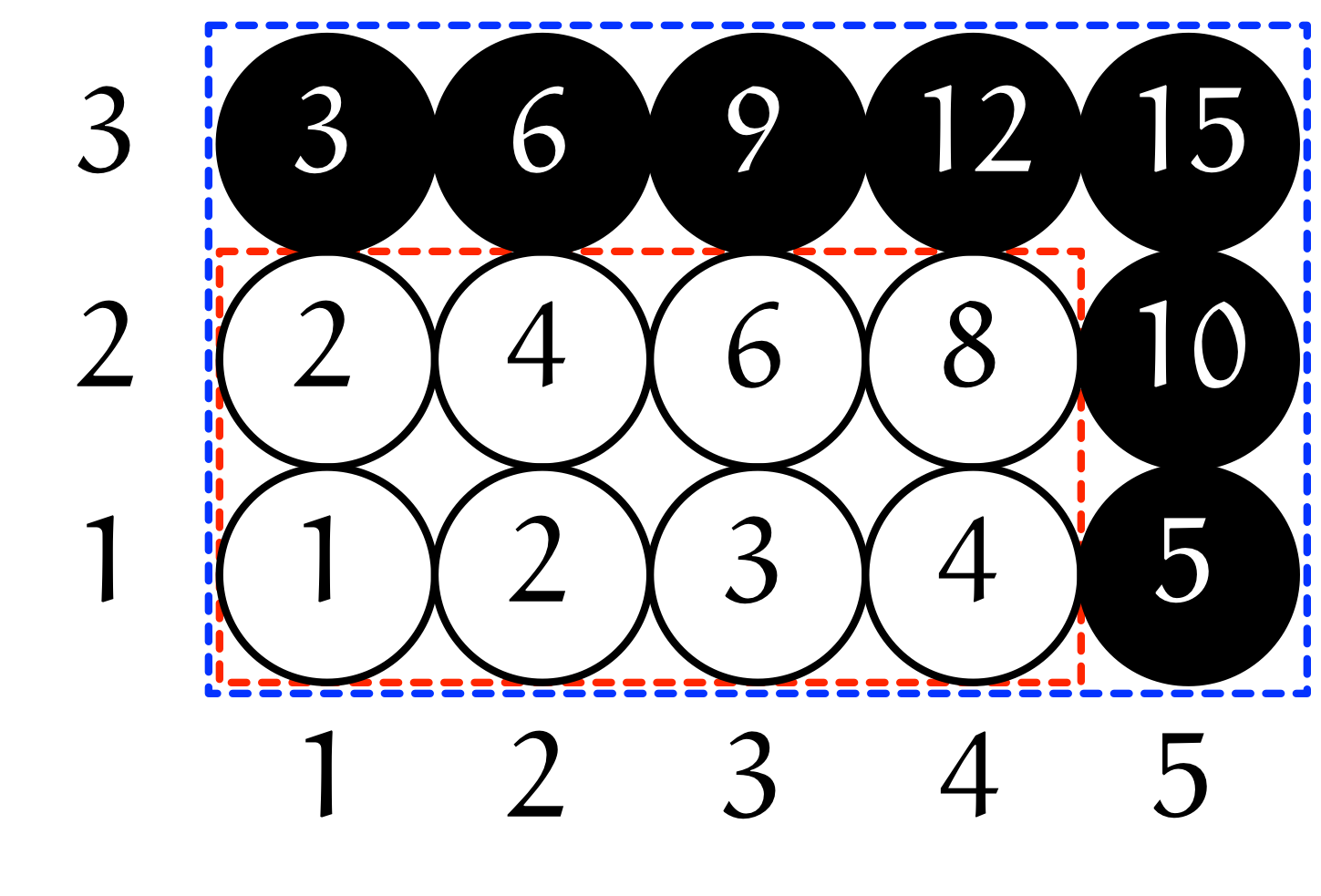
ユーリ「わかった！　白丸のところに来る数は $3$ でも $5$ でも割り切れない数になるんだ！」

僕「いやいや、そんなことないよ。だって $6$ はおもいっきり出てくる」

ユーリ「ありゃ。ほんとだ」

僕「……少し見えてきたぞ。《条件をすべて使ったか》だな！」

ユーリ「条件？」

僕「うん。ユーリの長方形のアイディアはとてもよさそう。 条件《$p,q$ は素数である》を使うんだ」