![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねーお兄ちゃん。お兄ちゃんだったら『$1$ とは何か』と聞かれたら、 何て答える?」
ユーリのクイズ
$1$ とは何か。
僕「また出し抜けに……」
ここは僕の部屋。
ユーリは中学生、僕よりも三歳年下のいとこである。
彼女は近所に住んでいて、休みになるといつも僕のところに遊びにくる。
今日もやってくるなり、僕にクイズを出してきた。
$1$ とは何か……
ユーリ「『しかし、そのとき、まだ彼は知らなかった。 その何気ない問いが、異世界への扉を開くことになろうとは……』」
僕「異世界転生ラノベを始めるなよ。それから地の文へのツッコミ自重」
ユーリ「ちぇっ」
僕「……それで『$1$ とは何か』が問題なんだね」
ユーリ「ねーねー、ユーリの答え、聞きたい?」
僕「はいはい。ユーリの答えは?」
ユーリ「『$1$ とは、いちばん小さい自然数である』ってゆーの」
僕「なるほど。自然数は $1,2,3,\ldots$ という数のことだから、 $1$ はその中でいちばん小さい。それはまあ、正しいね」
《自然数》
$1,2,3,\ldots$ のような数を自然数という。

ユーリ「え、なんで《まあ、正しい》なの?」
僕「ユーリの答えは、 自然数というものがすでに定義されているという仮定を置いているからね」
ユーリ「そんなこといったって、何にも仮定しなきゃ、何にもいえないじゃん?」
僕「確かにそれはそうだ。 だから《まあ、正しい》っていったんだよ。 学校では自然数は $1,2,3,\ldots$ と習うけど、 数学の本の中には、自然数に $0$ を含めて、 $0,1,2,3,\ldots$ が自然数だと定義しているものもあるよ」
ユーリ「へー、そーなんだ。まぎらわしいね」
僕「数学の本では、初めに『この本ではどのような数を自然数と呼ぶか』をきちんと定義しているから、 まぎらわしくなることはないよ。 それはそれとして、ユーリの答えは『$1$ とは、いちばん小さい自然数である』なんだね」
ユーリ「そだよん」
僕「そのクイズ、『$1$ とは何か』というクイズはユーリが考えたの?」
ユーリ「あのね、中学に入学したばかりのときにね、 最初の数学の授業で先生が聞いたんだよ。クラスのみんなに」
僕「そうなんだ」
ユーリ「数学の授業の、いっちばん最初に、 『ではみなさんは、 $1$ というものがほんとうは何かご承知ですか』 っていってた」
僕「『銀河鉄道の夜』みたいに?」
ユーリ「『銀河鉄道の夜』みたいに」
「ではみなさんは、そういうふうに川だと言われたり、 乳の流れたあとだと言われたりしていた、 このぼんやりと白いものがほんとうは何かご承知ですか。」
宮沢賢治『銀河鉄道の夜』
僕「なるほどねえ……もしかしたら『$1$ を問う』というのは、 数学の最初の授業にふさわしいことかもしれないね。 中学校に入学して、算数が数学になって、最初の問いかけ……うん、 $1$ 番目の問いかけだ」
ユーリ「そんで、一人一人、順番に答えさせられたんだよ」
僕「そのときユーリは、さっそうと『$1$ とは、いちばん小さい自然数である』って答えたの? かっこいいな!」
ユーリ「んにゃあ……てわけじゃないんだけど。 パッと答えられなかった。 でもね、他の人は、いろいろ答えてた。 《最初の数》とか《いちばん小さい数》とか《自然数》とか《整数》とか…… そだそだ、お兄ちゃんだったら『$1$ とは何か』って聞かれたら、何て答える?」
僕「『$1$ とは何か』……そうだなあ、なんて答えるだろう」

ユーリ「わくわく」
僕「そもそも『$1$ とは何か』っていう問いは何を尋ねてるんだろうか。
ユーリ「あっ、お兄ちゃんでもそーなんだ」
僕「たとえば、『日本の首都はどこか』と聞かれたら『東京』ってすぐに答えられるだろ? それは、 答えを知っているから。日本の首都は東京だと覚えているから。 でもね、もしも『東京とは何か』と聞かれたら、いったい何を尋ねているんだろうかと考えてしまうよ」
ユーリ「にゃるほどー……いろんな答えがありそーだにゃ」
ユーリは猫語で答える。
僕「うん、でも、最初の授業で『$1$ とは何か』を聞いた先生は、 正しい答えを聞きたかったわけじゃないと思うな」
ユーリ「は?」
僕「先生はきっと、 $1$ のことを心に思い浮かべてほしかったんだよ。クラスのみんなにね」
ユーリ「おー、なんという教師目線! そんでそんで? お兄ちゃんだったら『$1$ とは何か』にどう答える? ユーリはもう答えたよ。さあさあさあさあ……」
僕「迫ってくるなよ。僕が思いついたのは『$1$ とは、方程式 $$ x^2 = x $$ を満たす正の数のことである』……という答えなんだけど、いまいちかな」
ユーリ「いきなり方程式とか持ち出すんだ」
僕「うん。できるだけ何も仮定しないで、 $1$ というものが何かいえないかな、 と思ったんだよ。《$x^2 = x$ を満たす $x$》というのは《$2$ 乗しても自分自身のままの数》ってことだよね。 だから、自分を使って自分を定義できると考えた。 でも、 $x^2 = x$ を満たすのは $x = 1$ だけじゃなくて、 $x = 0$ も満たしちゃうから、 だから《正の数》という条件を付けたんだよ。 自分自身で自分を定義できるっておもしろいから」
ユーリ「ふーん……何だか変なの。だって『$1$ とは何か』に答えるのに《$2$ 乗》を使うっておかしくない? 自分で自分を定義とか言いつつ、 $2$ を使ってるじゃん。 $2$ が使えるなら、 『$1$ とは、 $2$ を $2$ で割った数』でもいーじゃん?」
僕「おっと! 確かにユーリのいう通りだな……いやいや、ちがうよ。 $2$ という数を使うんじゃなくて、 $xx = x$ という方程式だと考えればいいんだ。 『$1$ とは、自分自身と掛け算しても変化しない正の数である』として $1$ を定める。 これなら $2$ という数は出てこないだろ?」
ユーリ「ほほー……そー来ましたか。 いやいや、だめですぜ。お兄ちゃんが出してきた《正の数》って条件は《$0$ より大きい》って条件でしょ? だったら、 $2$ は出てきてないけど、今度は $0$ を出してきてるわけじゃん」
僕「うーん、ごもっとも。『$1$ とは何か』に答えるのは、なかなか難しいな」
ユーリ「作ったことあったよね」
僕「何を?」
ユーリ「数! 何もないところから、 $0,1,2,3,\ldots$ って数を作ったじゃん。 《ノイマンの方法》で」
僕「ああ、そうだったね(第151回参照)」
ユーリ「$1,2,3,\ldots$ が自然数で、 $\ldots,-3,-2,-1,0,1,2,3,\ldots$ が整数だよね」
僕「そうだね」
《整数》
$\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots$ のような数を整数という。
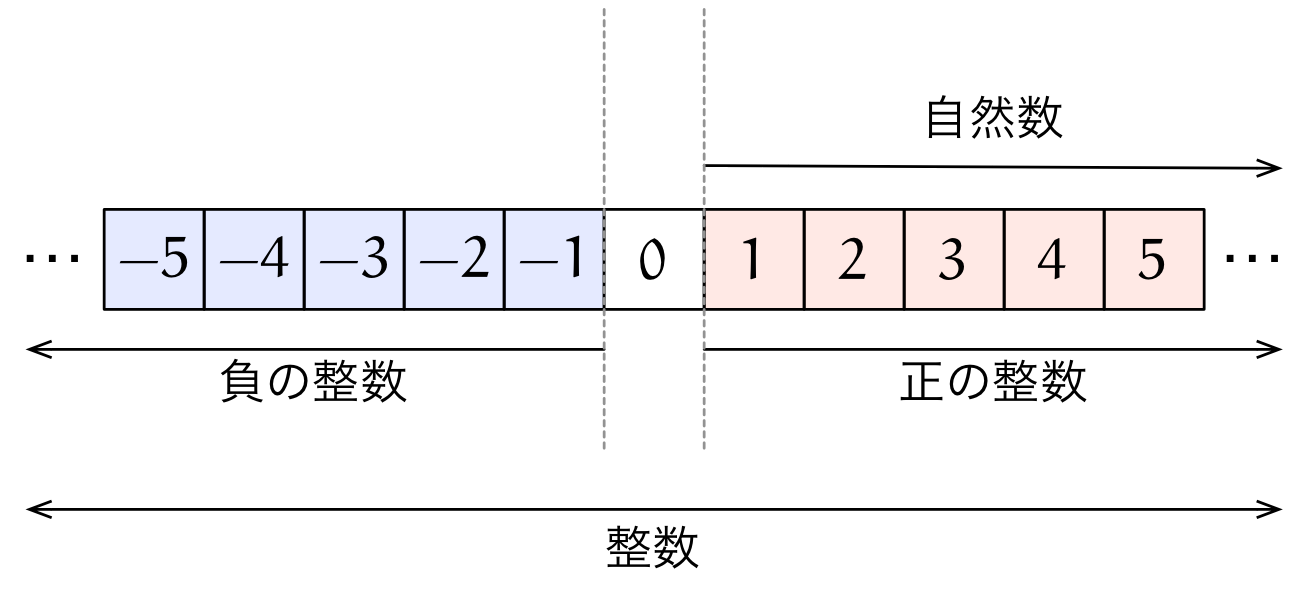
ユーリ「ふんふん」
僕「《例示は理解の試金石》だから、具体例を作ってみよう」
ユーリ「$0$ は整数である……とか?」
僕「そうそう。 $-17$ は整数である。 $2501$ は整数である」
ユーリ「$2501$ is 何」
僕「整数である具体例だけじゃなく、整数ではない具体例もね」
ユーリ「$0.5$ は整数じゃない……とか?」
僕「そうだね。 $\frac{17}{2}$ は整数ではない。 $250.1$ も整数ではない」
ユーリ「円周率 $3.1415926535\cdots$ も整数じゃない」
僕「整数を決めてしまえば、倍数は難しくないね」
ユーリ「$2$ の倍数は、 $$ \ldots, -6, -4, -2, 0, 2, 4, 6, \ldots $$ とか」
僕「そうだね。 $3$ の倍数は、 $$ \ldots, -9, -6, -3, 0, 3, 6, 9 \ldots $$ だね」
$2$ の倍数

$3$ の倍数

ユーリ「ふんふん」
僕「《$2$ の倍数》はどれをとってみても、 $$ 2\times\REMTEXT{整数} $$ という形で書けるよね。こんなふうに」
《$2$の倍数は、$2\times\REMTEXT{整数}$の形》 $$ \begin{align*} & \vdots \\ -6 & = 2 \times (-3) \\ -4 & = 2 \times (-2) \\ -2 & = 2 \times (-1) \\ 0 & = 2 \times 0 \\ 2 & = 2 \times 1 \\ 4 & = 2 \times 2 \\ 6 & = 2 \times 3 \\ & \vdots \\ \end{align*} $$
ユーリ「そだね。《$3$ の倍数》は、 $$ 3\times\REMTEXT{整数} $$ という形」
《$3$の倍数は、$3\times\REMTEXT{整数}$の形》 $$ \begin{align*} & \vdots \\ -9 & = 3 \times (-3) \\ -6 & = 3 \times (-2) \\ -3 & = 3 \times (-1) \\ 0 & = 3 \times 0 \\ 3 & = 3 \times 1 \\ 6 & = 3 \times 2 \\ 9 & = 3 \times 3 \\ & \vdots \\ \end{align*} $$
僕「そうだね。一般化して《$m$ の倍数》を定義できる」
ユーリ「出たな一般化」
僕「《$m$ の倍数》というのは、 $m\times n$ つまり $mn$ という形で表せる数と定義できる」
ユーリ「《$m$ の倍数》は簡単だよねー」
僕「そうかな?」
《倍数》
$a, m$ は整数とする。ここで、 $$ a = mn $$ という等式を満たす整数 $n$ が存在するとしよう。
このとき《$a$ は、 $m$ の倍数である》という。
ユーリ「要するに《$m$ の倍数》は $mn$ だってことでしょ? 簡単じゃん。何が難しーの?」
僕「《例示は理解の試金石》だから、具体例を作ってみようか」
ユーリ「$6$ は $3$ の倍数である。以上!」
僕「じゃあ、こういうクイズはどう?」
クイズ
$6$ は $3$ の倍数である。それはなぜか。
ユーリ「は? なぜか? だって、 $3$ の倍数は、 $\ldots, -9, -6, -3, 0, 3, 6, 9, \ldots$ でしょ? $6$ が入ってるじゃん」
僕「そうだね。そのことを、倍数の定義を使って答えるとどうなるか、というクイズだよ」
ユーリ「あー、はいはい。定義に従えと……えーとね、 $$ 6 = 3\times2 $$ だから、 $6$ は $3$ の倍数」
僕「いいね。 等式 $6 = 3 \times n$ を満たす整数 $n$ は存在する。具体的にいえば $2$ だ。 だから、倍数の定義より、 $6$ は $3$ の倍数といえる」
クイズの答え
$6$ は $3$ の倍数である。それは、 $6 = 3\times n$ を満たす整数 $n = 2$ が存在するからである。
ユーリ「あーくどい。 じゃ、お兄ちゃんに逆襲クイズだよ」
逆襲クイズ
$7$ は $3$ の倍数ではない。それはなぜかにゃ?
僕「なるほど。 答えはこうなるね。 等式 $7 = 3 \times n$ を満たす整数 $n$ は存在しない。 だから、 $7$ は $3$ の倍数じゃない。 すばらしいクイズだなあ、ユーリ」
クイズの答え
$7$ は $3$ の倍数ではない。それは、 $7 = 3\times n$ を満たす整数 $n$ が存在しないからである。
ユーリ「その《すばらしいクイズ》って皮肉?」
僕「違うよ。 ユーリはちゃんと、 $3$ の倍数である具体例と、 $3$ の倍数ではない具体例を作ったからだよ。すごいすごい!」
ユーリ「お兄ちゃんがコーフンしているポイントはわかんないけど、 もっとホメてもいいよん」
僕「じゃあ、ユーリにクイズ」
ユーリ「ホメるとは何か」
クイズ
どんな整数 $m$ に対しても《$0$ は、 $m$ の倍数である》といえるか。

ユーリ「あー……いえる!」
僕「はい正解。それはなぜ?」
ユーリ「だって、 $0$ は $2$ の倍数でしょ。それに $0$ は $3$ の倍数でもあるし、 $4$ の倍数でも……ずーっとね」
僕「定義からいえば?」
ユーリ「そっか、定義かー……えっとね、 $0 = m\times 0$ だから?」
僕「そうだね。ちゃんというなら…… 《$0$ は、 $m$ の倍数である》というためには、 $$ 0 = mn $$ という整数 $n$ が存在すればいいんだよね、倍数の定義から。 ところで、 $n = 0$ としてみよう。そうすれば、 $mn$ は必ず $0$ に等しくなる。 $mn = m \times 0 = 0$ だから。 ということは、 どんな整数 $m$ に対しても《$0$ は、 $m$ の倍数である》といえるわけだね」
クイズの答え
どんな整数 $m$ に対しても《$0$ は、 $m$ の倍数である》といえる。
ユーリ「ふんふん。めっちゃくどいけどねー」
僕「じゃあ、こんなクイズは?」
クイズ
$0$ は、 $0$ の倍数といえるか。

ユーリ「そりゃいえるよ!」
僕「その理由は?」
ユーリ「理由? また定義だね! 《$0$ は、 $0$ の倍数》だといえるよ。 だって、 $0 = 0 \times 0$ だから」
僕「そうだね。《$0$ は、 $0$ の倍数》というためには、 $0 = 0\times n$ を満たす整数 $n$ が存在することをいえばいい。 $n = 0$ でもいいけど、何でもいい」
ユーリ「そっか、 $n$ は……なんでもいーんだ」
僕「そうだね。 $n$ は $1$ でも $2$ でも $123$ でも何でもいい。 $0 = 0 \times n$ を満たす整数 $n$ はひとつじゃないけど、とにかく存在する。 だから、《$0$ は、 $0$ の倍数》といえる」
ユーリ「このくどい感じ……嫌いじゃないぜ」
クイズの答え
$0$ は、 $0$ の倍数といえる。
僕「じゃ、もう一つクイズ」
クイズ
$-3$ は、 $0$ の倍数といえるか。

ユーリ「そりゃ……いえないいえない!」
僕「じゃ、その」
ユーリ「その理由はね、倍数の定義からわかるの。 $-3 = 0\times n$ になる整数 $n$ は存在しないから。 どんな $n$ でも $0\times n$ は $0$ になっちゃうから、 $-3$ になんてできない!」
僕「そうだね。 $-3 = 0\times n$ という等式を満たす整数 $n$ は存在しないから、 $-3$ は $0$ の倍数とはいえない。倍数の定義から、いえない」
ユーリ「ねーお兄ちゃん、ちょっと気持ちいいね。めちゃめちゃくどいけど、気持ちいい」
僕「何が?」
ユーリ「あのね。 定義からバシッと決まるところ。 《どうして?》って聞かれたときに《だって、それは定義からいえるじゃん!》でバッサリ。 そこが気持ちいい」
僕「なるほどね。 『それは定義からいえる』や『それは定義からいえない』というのは確かに問答無用だ」
ユーリ「だよねー」
僕「僕は、覚えてなくても答えられる点が好きだな」
ユーリ「?」
僕「たとえば、 $6$ は $3$ の倍数であるとか、 $12$ は $3$ の倍数であるというのは、 よく使うから覚えている。でも、 《$0$ は、 $3$ の倍数か》は覚えていないかもしれない。 でも、たとえ覚えていなくても、知らなくても、 定義にあてはめて考えると答えがでる。そこがいいな」
ユーリ「$0$ が $3$ の倍数だって、知ってるよ。常識なのでは」
僕「ユーリにとってはね。こんなクイズは?」
クイズ
どんな整数 $n$ に対しても《$n$ は、 $1$ の倍数である》といえるか。

ユーリ「これはもちろん、いえる! だってね、 $n = 1 \times n$ と書けるでしょ。 $n$ は整数。 倍数の定義から、いえる! 問答無用! バシッ!」
僕「そうだね。どんな整数も $1$ の倍数といえる。 ふだん《$1$ の倍数》なんて考えないし、九九を覚えるときでも $1$ の倍数なんて、わざわざ覚える必要がない。 でも、倍数の定義から、どんな整数も $1$ の倍数であるといえる」
クイズの答え
どんな整数 $n$ に対しても《$n$ は、 $1$ の倍数である》といえる。
僕「ところで、倍数を図に描くと、きれいなパターンになるよ」
倍数が生み出すパターン
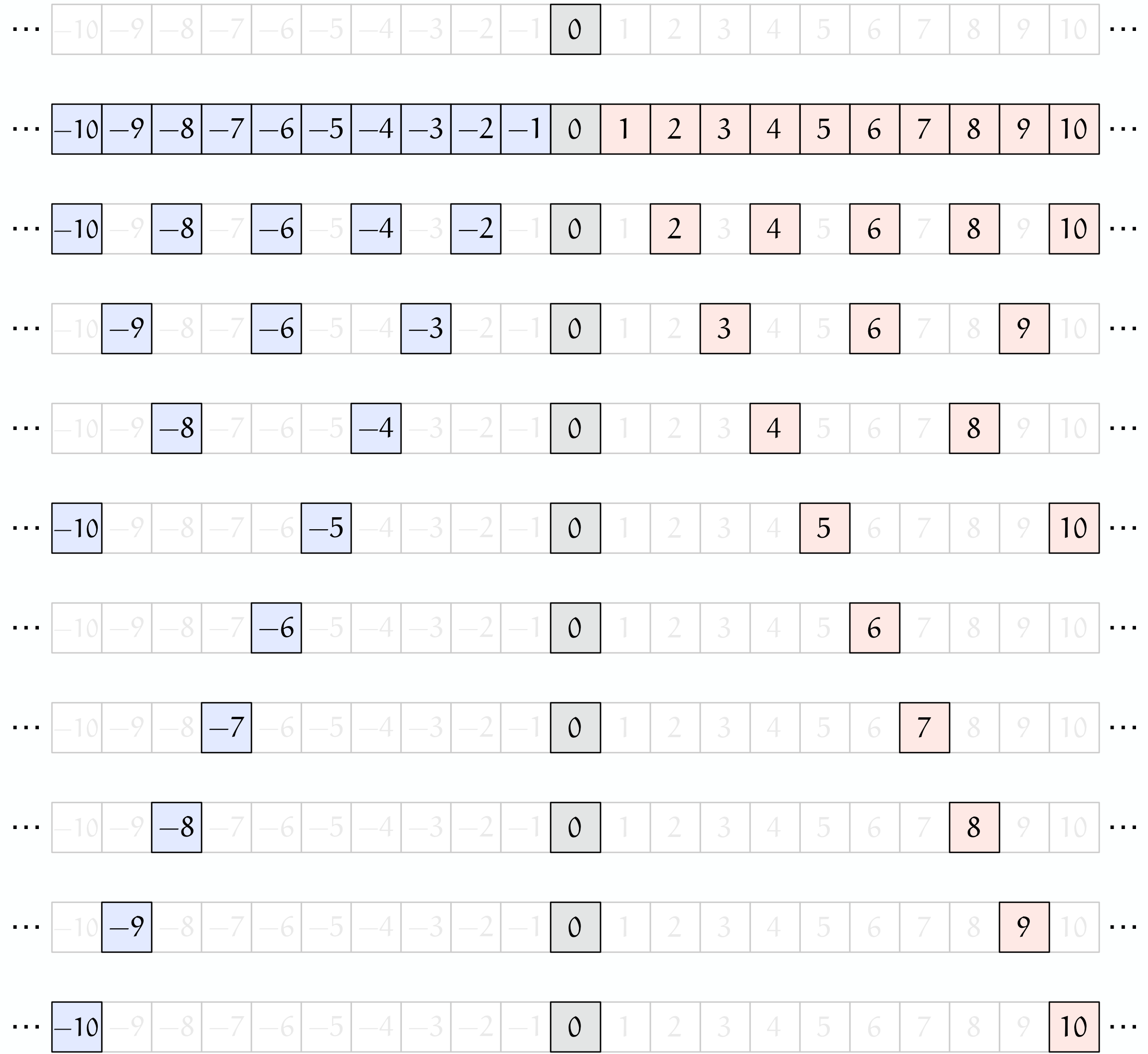
ユーリ「ほほー! 意外ときれーだね!」
僕「これは、上から $0$ の倍数、 $1$ の倍数、 $2$ の倍数、 $3$ の倍数……」
ユーリ「わかるわかる! あたりまえだけど、だんだん広がってくんだ」
僕「そういうこと。このパターンを見ると発見があるよ。どの倍数にも、必ず $0$ が入ってる」
ユーリ「ふんふん。縦一列に黒い $0$ あるもんね」
僕「これは、どんな整数 $m$ に対しても《$0$ は、 $m$ の倍数である》に相当している」
ユーリ「え? あ、そだね」
僕「それから、《$0$ は、 $0$ の倍数である》は、いちばん上の $0$ の倍数を見ればわかる」
ユーリ「そっか、《$0$ の倍数》って $0$ だけなんだね。そりゃそっか」
僕「きれいな図ってだけじゃなくて、パターン一つ一つが数学と対応ついているのがいいんだ」
ユーリ「図で見た方がずっとわかりやすいね」
僕「見える範囲ではね。でも、たとえば《$1000000$ の倍数》と言われたら図にするのは難しいけど」
僕「図を描いたら、公倍数も考えやすいかな」
ユーリ「こうばいすう」
僕「公倍数の定義はこうだよ」
公倍数
$a,m,n$ は整数とする。ここで、
$a$ は $m$ の倍数であり、しかも、 $a$ は $n$ の倍数でもあるとしよう。
このとき《$a$ は、 $m$ と $n$ の公倍数である》という。
ユーリ「公倍数は知ってるけど……」
僕「《$2$ と $3$ の公倍数》を図にしてみようか。 まずね、《$2$ の倍数》と《$3$ の倍数》をこんなふうに並べてみる」
《$2$ の倍数》と《$3$ の倍数》

ユーリ「……」
僕「そして、《$2$ の倍数》と《$3$ の倍数》の両方になっている数を見つけ出すと、公倍数の定義から、それが《$2$ と $3$ の公倍数》になってる」
《$2$ の倍数》と《$3$ の倍数》から、《$2$ と $3$ の公倍数》を作る

ユーリ「……」
僕「ね?」
ユーリ「お兄ちゃん! だったらね、こーゆーのもいいんじゃない? あのね、《$2$ の倍数》を縦線にして、 《$3$ の倍数》を横線にするの。そしたら、ぶつかったところが《$2$ と $3$ の公倍数》! $0$ 以上のところだとこんな感じの図!」
これで《$2$ と $3$ の公倍数》(?)
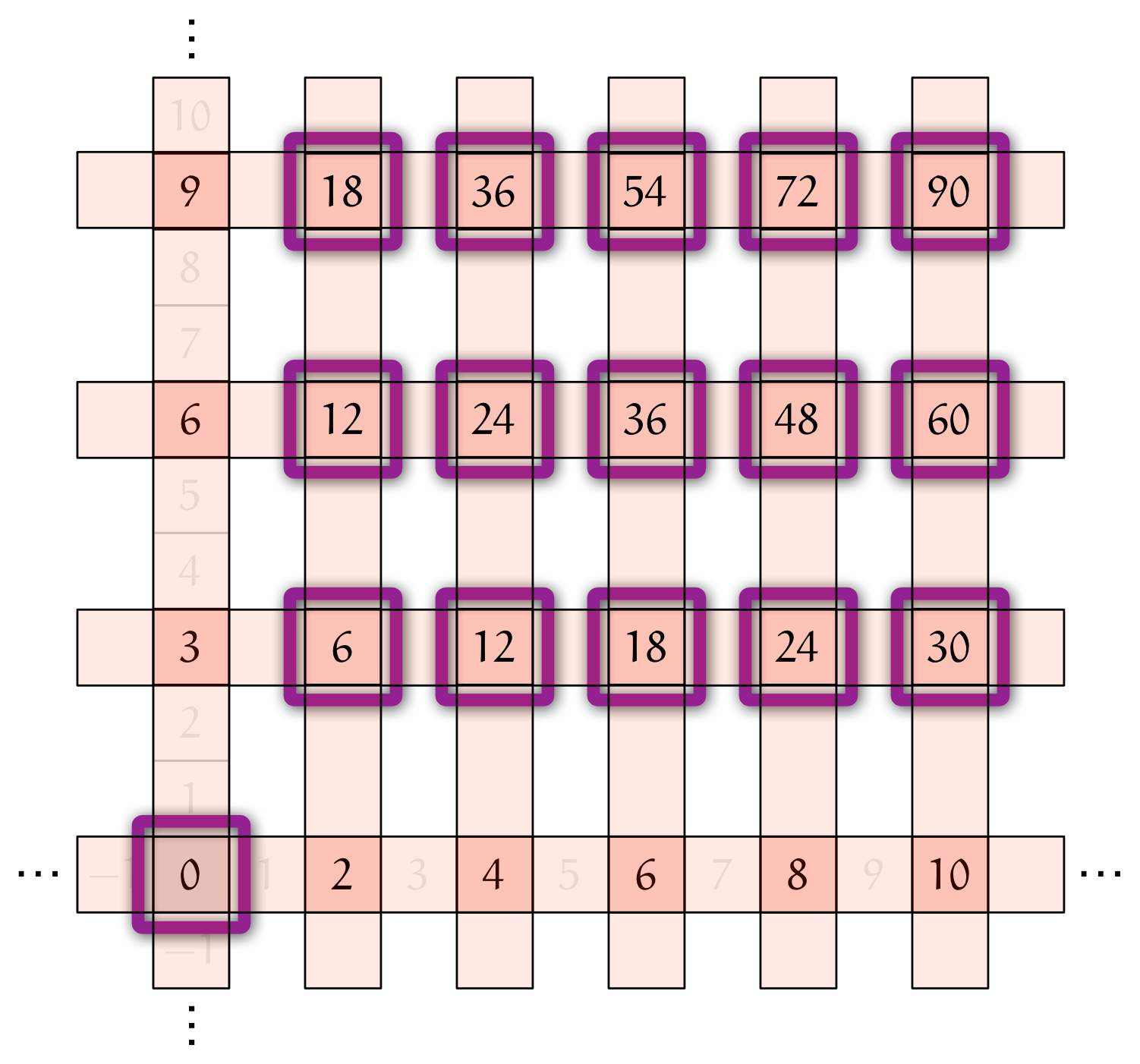
僕「おお! ……え、ちょっと待ってよ、ユーリ。これはいいんだけど……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第191回終わり)
(2017年4月21日)