第192回 シーズン20 エピソード2

倍数って何だろう（後編）

公倍数

僕「図を描いたら、公倍数も考えやすいかな」

ユーリ「こうばいすう」

僕「公倍数の定義はこうだよ」

ユーリ「公倍数は知ってるけど……」

僕「《$2$ と $3$ の公倍数》を図にしてみようか。 まずね、《$2$ の倍数》と《$3$ の倍数》をこんなふうに並べてみる」

ユーリ「……」

僕「そして、《$2$ の倍数》と《$3$ の倍数》の両方になっている数を見つけ出すと、公倍数の定義から、それが《$2$ と $3$ の公倍数》だね」

ユーリ「……」

僕「ね？」

ユーリ「お兄ちゃん！　こーゆーのもいいんじゃない？　あのね、《$2$ の倍数》を縦線にして、 《$3$ の倍数》を横線にするの。そしたら、ぶつかったところが《$2$ と $3$ の公倍数》！」

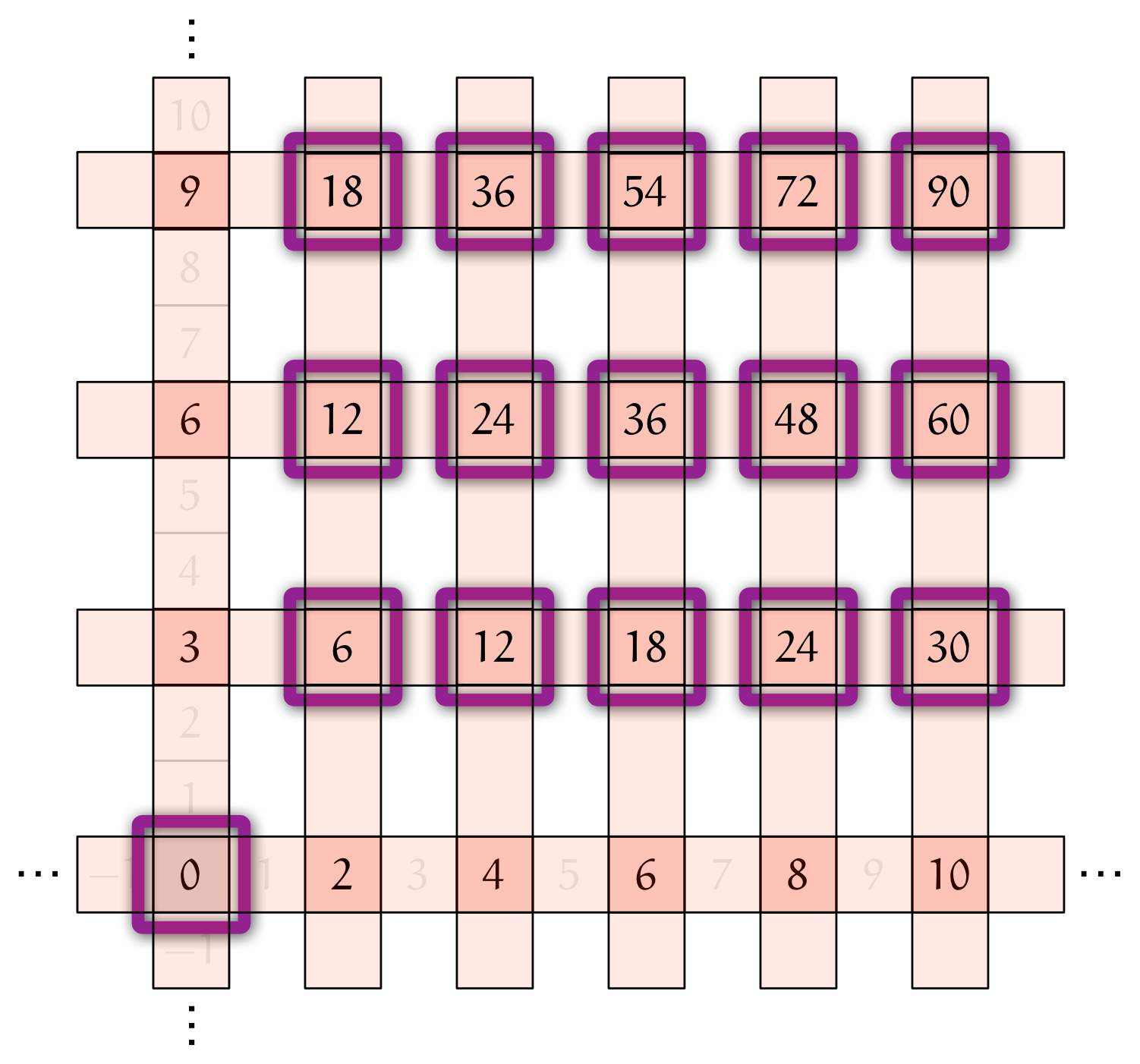
僕「おお！　……え、ちょっと待ってよ、ユーリ」

ユーリ「おかしくないでしょ？　だって、 $2$ と $3$ の公倍数は、 $0,6,12,18,24,30,36,\ldots$ だし。 《ユーリの図》にちょうど出てくるじゃん？」

僕「うん、それはいいんだけど……」

ユーリ「あー、同じ数があちこちに出てくるのが気になるの？　 しょーがないじゃん。たとえば $12$ は、 $$ 12 = 2 \times 6 = 3 \times 4 $$ みたいに、いろんな掛け算のしかたができるもん」

僕「いやいや、それはわかっているよ。 《$2$ と $3$ の公倍数》は《ユーリの図》でいいんだ。 気にしているのはそこじゃなくて、 もっと一般的に考えると、いったいどうなるかということ」

ユーリ「来たぞ来たぞ。《一般的に考える》]

僕「……」

ユーリ「じゃ、《$3$ と $4$ の公倍数》でもやってみる！

　《$3$ の倍数》は、 $\UL{0},3,6,9,\UL{12},15,18,21,\UL{24},27,\ldots$

　《$4$ の倍数》は、 $\UL{0},4,8,\UL{12},16,20,\UL{24},28,\ldots$

これの、両方に出てくる数を調べればいーんでしょ。

　《$3$ と $4$ の公倍数》は、 $\UL{0},\UL{12},\UL{24},\ldots$

だよね」

僕「……」

ユーリ「《ユーリの図》にしてみると……ほらー！　やっぱり、うまくいくじゃん？」

僕「うん、そうだね。《$3$ と $4$ の公倍数》のときもうまくいく。 でも、一般的に《$m$ と $n$ の公倍数》のときは、 《ユーリの図》ではうまくいかないんだよ。 たとえば《$4$ と $6$ の公倍数》でやってごらんよ」

ユーリ「へーい。

　《$4$ の倍数》は、 $\UL{0},4,8,\UL{12},16,20,\UL{24},28,32,\UL{36},40,44,\UL{48},\ldots$

　《$6$ の倍数》は、 $\UL{0},6,\UL{12},18,\UL{24},30,\UL{36},42,\UL{48},\ldots$

だから、ええと、

　《$4$ と $6$ の公倍数》は、 $\UL{0},\UL{12},\UL{24},\UL{36},\UL{48},\ldots$

になるよね。《ユーリの図》を描くと……」

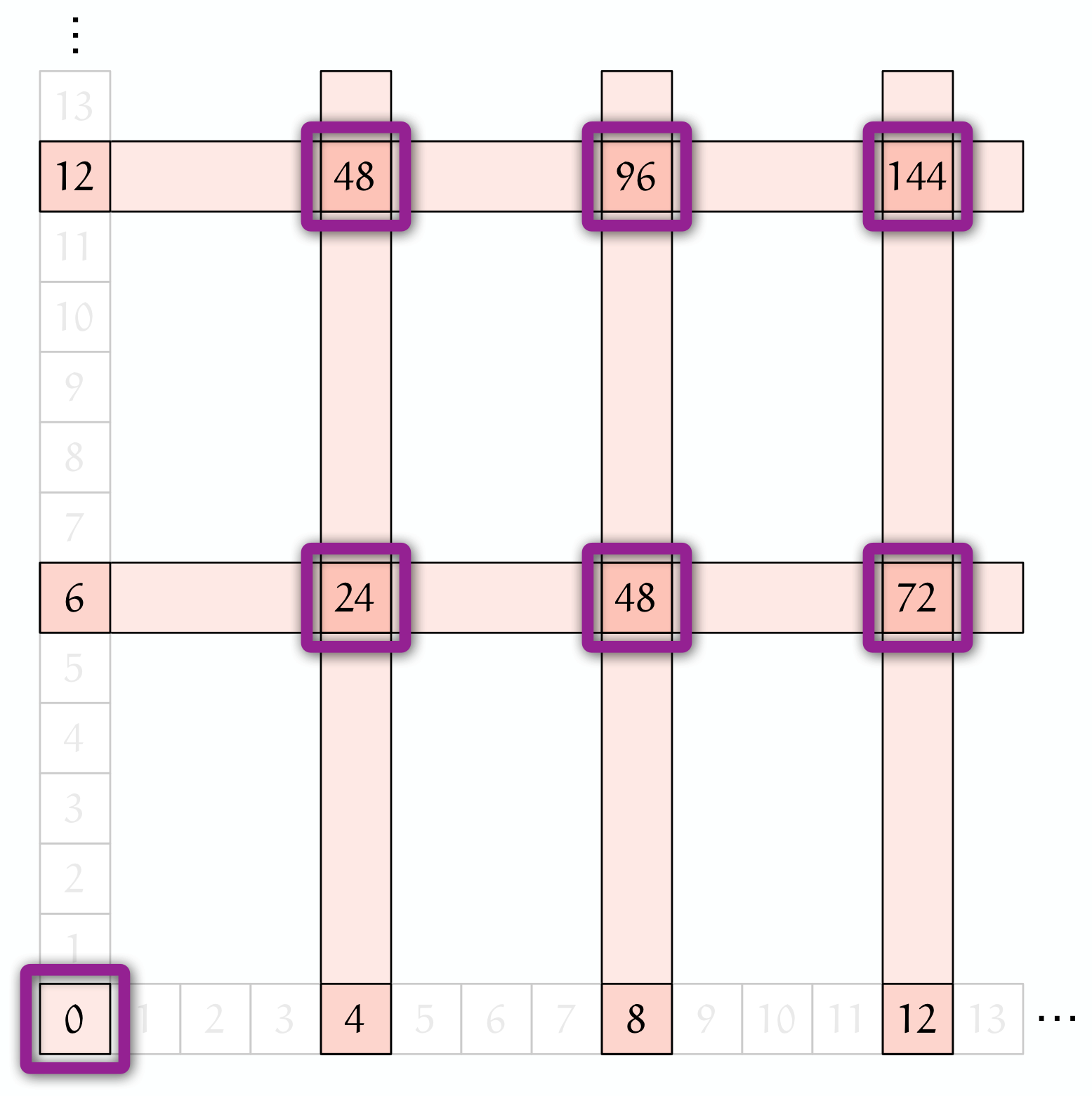
ユーリ「ありゃ。ほんとだ。 $0,24,48,\ldots$ になっちゃう。《$4$ と $6$ の公倍数》になってない！」

僕「$12$ が消えちゃったよね」

ユーリ「$36$ も消えてる！」

僕「どうしてか、わかる？」

ユーリ「えーと……」

僕「《ユーリの図》では何をやっていたかを考えるんだよ」

ユーリ「わかってるって！」

• $m$ の倍数を縦線にして、
• $n$ の倍数を横線にして、
• 縦と横の線がクロスしたところに、……あっ！　わかった！

僕「わかった？」

ユーリ「そっか。 縦と横の線がクロスしたところに出てくる数は、

　《$m$ と $n$ の公倍数》

じゃないんだね。クロスしたところに出てくるのは、

　《$mn$ の倍数》

になっちゃうんだ！」

僕「そういうことになるね。ちゃんと式で書いてみようか。 $0$ 以上の整数で考えることにするよ。 $m$ の倍数を縦線にしたのは、 $$ 0m, 1m, 2m, 3m, 4m, 5m, \ldots $$ という数になるね。一般的に書くなら、 $am$ となる。 $a = 0,1,2,3,\ldots$ として」

ユーリ「ふんふん。だったら、 $n$ の倍数の横線は、 $$ 0n, 1n, 2n, 3n, 4n, 5n, \ldots $$ という数で、一般的に書くと、 $bn$ という形だね。 $b = 0,1,2,3,\ldots$ として」

僕「そうそう。そして、クロスしたところに出てくる数は、 $$ am \times bn = abmn $$ になる。 $a$ も $b$ も $0,1,2,3,\ldots$ の範囲を自由に動けるから、 $ab$ も $0,1,2,3,\ldots$ の範囲を自由に動ける。だから、 クロスしたところに出てくる数は、《$m$ と $n$ の公倍数》じゃなくて《$mn$ の倍数》になる」

ユーリ「そっか。そーなるのかー。 そもそも、《$m$ と $n$ の公倍数》と《$mn$ の倍数》は違うんだ！」

僕「正確には、 《$m$ と $n$ の公倍数》と《$mn$ の倍数》は同じとは限らない、だね」

ユーリ「同じときもあるから？」

僕「そういうこと。《$2$ と $3$》や《$3$ と $4$》のときは同じになったよね」

ユーリ「でも、 $4$ と $6$ のときは違う」

ユーリ「$12$ が抜けてるし、 $36$ も抜けてる」

僕「そうだね。 $12$ がどんな形で書けるかを考えてみる。 $$ 12 = 3\times\UL{4} = 2\times\UL{6} $$ だから、 $12$ は $\UL{4}$ の倍数でもあるし、 $\UL{6}$ の倍数でもある」

ユーリ「ふんふん」

僕「でも、 $12$ や $36$ は、 $\UL{4}\times\UL{6} = 24$ の倍数にはなっていない。 だから、《ユーリの図》には出てこなかった」

ユーリ「そだね。……簡単だと思ってたけど、公倍数って意外と難しーね」

僕「難しい？」

ユーリ「公倍数って、結局《$4$ の倍数》と《$6$ の倍数》を並べて、両方に出てくるのを探すってことでしょ。めんどいじゃん」

僕「だから、《素因数分解》が大事になるんだよ、ユーリ」

ユーリ「そいんすうぶんかい」

素因数分解

僕「そうだよ。素因数分解。 $4$ という数があって、 $6$ という数もある。 その数がどんな性質を持っているかを僕たちは調べたい。 深く調べたい。二つの数がどんな関係にあるかを深く、深く調べたい。 《$4$ と $6$ の公倍数》を求めるというのは、 数を深く研究するための第一歩でもあるんだよ！」

ユーリ「あっはい……盛り上がってるとこ悪いけど、そんで、素因数分解？」

僕「そうだね。 $4$ と $6$ をただ眺めているだけでは何もわからない。 いまは倍数……つまり掛け算に関心があるんだから、 $4$ や $6$ をそれぞれ掛け算で表してみるのは自然な考えだね。 ある数を《素因数分解する》というのは、その数を《素数の掛け算の形で表す》ということ」

ユーリ「ふんふん。そだね」

僕「素数は、もう分解できない。 もっと正確にいうと……素数は、 $1$ より大きな整数の積の形で表せない。 素数じゃない $6$ は、 $2\times3$ のように積の形に分解できる。 でも、素数の $2$ や $3$ は、積の形に分解できない」

ユーリ「うん」

僕「だから《素因数分解する》っていうのは、 《整数の積の形に分解しつくす》ということ。 それ以上はもう細かくできない！　というところまでもっていくこと。 分解し尽くしてから、詳しく研究するんだね。 たとえば、 $36$ を $1$ より大きな整数の積の形に分解していくと…… $$ \begin{align*} 36 &= 4 \times 9 \\ &= 2 \times 2 \times 9 \\ &= 2 \times 2 \times 3 \times 3 \\ \end{align*} $$ ……こうなる。そして $2\times2\times3\times3$ より細かくは分解できない。 $1$ や $\frac12$ を使えば別だけど」

ユーリ「$4$ と $6$ を素因数分解したら、 $4 = 2\times2$ で、 $6 = 2\times3$ でしょ？」

僕「そうだね。《$4$ と $6$ の研究》をするとき、 $$ 4 \quad\REMTEXT{と}\quad 6 $$ を見比べるだけでは、何もわからない。でも、 素因数分解して、 $$ 2\times2 \quad\REMTEXT{と}\quad 2\times 3 $$ を見比べてみると、共通な……」

ユーリ「あっ、お兄ちゃんが言いたいこと、わかったかも。 $2\times2$ と $2\times3$ だと両方に $2$ があるよね？　そゆこと？」

僕「そうだね。 $2\times2$ と $2\times3$ では両方に共通の素数がある。 この場合は $2$ だね。共通の素因数があるわけだ。 $4$ と $6$ には、 $2$ という共通の素因数がある。だから、 《$4$ と $6$ の公倍数》と《$4\times6$ の倍数》は違うものになるんだ」

ユーリ「んっ……」

僕「……」

ユーリ「お兄ちゃん！　わかった！」

僕「うん、ユーリはずっと何を考えていたんだろう」

ユーリ「いろいろ！」

僕「なるほど、いろいろね」

ユーリ「$4$ と $6$ には共通の素因数 $2$ があるでしょ。 そんとき、どーして《$4$ と $6$ の公倍数》と《$4\times6$ の倍数》は違うのか、わかったよ！」

僕「ふむふむ？」

ユーリ「その $2$ がだぶるからなんだね！　なーるほどー」

僕「そうだね。ユーリの話、もっと聞きたいな」

ユーリ「お兄ちゃん、素因数分解のこと言ってたじゃん？ 　《$4$ と $6$》のまま考えるんじゃなくて、 《$2\times2$ と $2\times3$》にして考えるの。 素因数分解すると詳しく研究できる」

僕「うんうん」

ユーリ「だから、ユーリはね、《$4$ と $6$ の公倍数》を素因数分解することを考えてたの」

僕「なるほど！」