第183回 シーズン19 エピソード3

バビロニアの数学（前編）

双倉図書館にて

ユーリ「あー楽しかったね、お兄ちゃん！」

僕「うん、思ったよりずっとおもしろかった」

ユーリ「ヒエログリフの暗号を解読したみたい。ねー、次はどっちに行く？」

僕「それより、ミルカさんやテトラちゃんを探さなくちゃ」

ユーリ「だーいじょぶだって。会えるって。 それより、あっちの部屋を見てみよーよ！　……ばびろにあ？」

僕「バビロニアの数学？　そうか、部屋ごとに時代がわかれているということなんだね」

ユーリ「あ、リサ姉（ねー）だ！

リサ「？？」

僕「そうか、このイベントのスタッフ作業中？」

リサ「半分作業、半分趣味」（咳）

ユーリ「お兄ちゃん、こっちのパネルから見ていくみたいだよ。 《ばびろにあ》の数字」

僕「これは $1$ と $10$ だけだね。バビロニアは十進法なのかな」

ユーリ「こっちに $1$ から $9$ までのパネルがある。なんだかギザギザ」

僕「なるほど。 $4$ や $7$ はちょっと変わっているけど、要するに $1$ を並べているんだね」

ユーリ「なーんだ。ヒエログリフとおんなじなんだね」

僕「次のパネルは、 $10$ 以上が展示してある」

ユーリ「これも似ているね」

僕「確かに似てるな。古代エジプトだと、縦棒が $1$ で、Ｕ字をひっくり返したのが $10$ だった。 バビロニアでも、縦棒が $1$ で、くの字が $10$ なんだ。仕組みは同じだね」

ユーリ「予言者ユーリとしてはですなー、 $20$ もわかるぞよ。《くの字》が $2$ 個ならぶと $20$ なんじゃよ。 $10$ が $2$ 個で $20$ を表すんじゃ」

僕「どれどれ？」

ユーリ「ほらね、ほーらね！　ばっちり正解さ！　この調子で $99$ まで行くんだよ、きっと」

僕「次のパネルは $30$ から $39$ だよね」

ユーリ「ごらんのよーに、予言どおりじゃ。わかったかの？」

僕「はいはい。次のパネルは $40$ から $49$ かな」

ユーリ「次のパネルでは、《くの字》が $4$ 個横に並び、《縦棒》が右に並ぶのじゃよ」

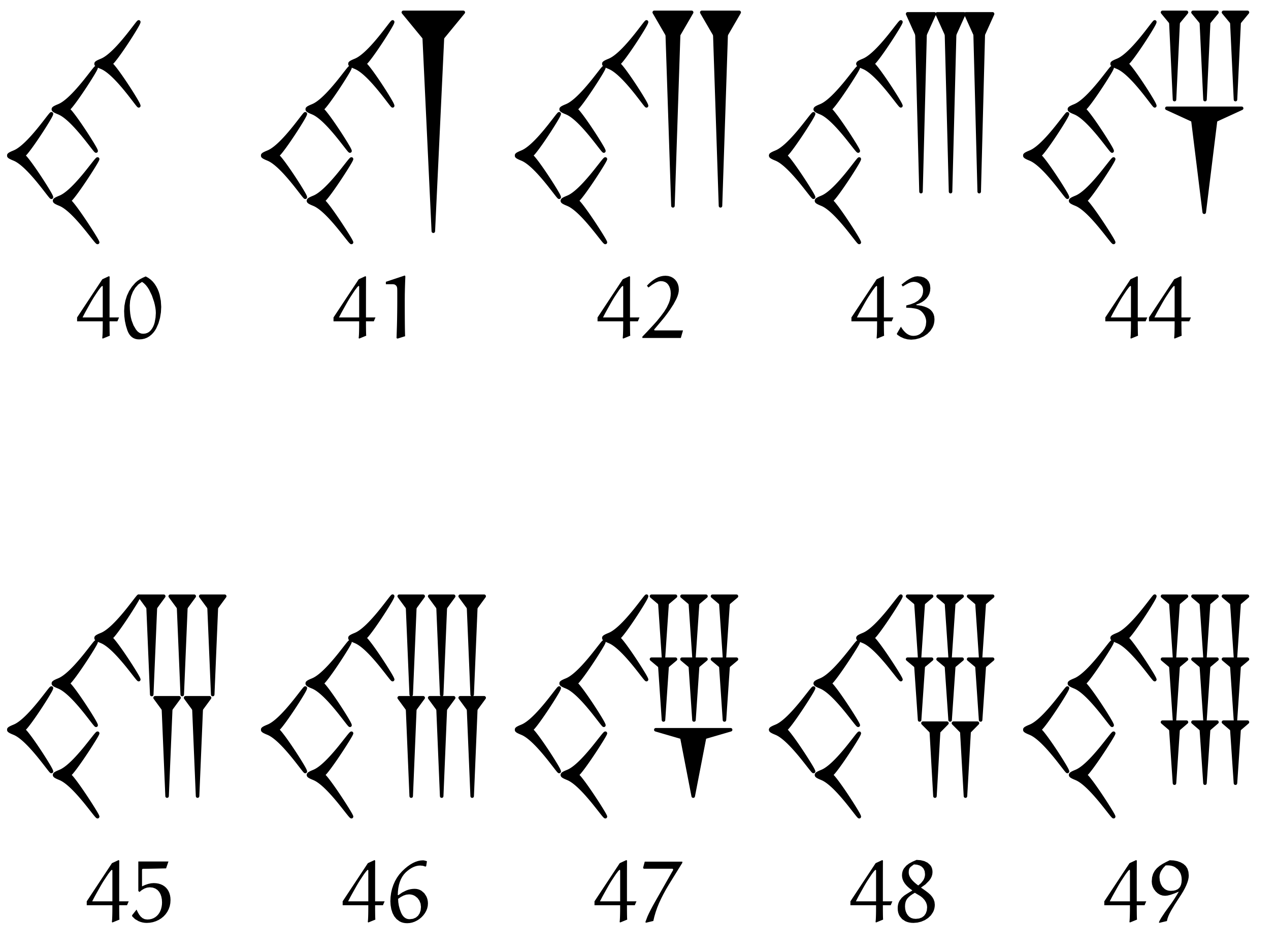
僕「惜しかったね。《くの字》は横に並んでないよ。予言者どの」

ユーリ「くっ……こ、これは、バビロニアの民の《でざいん》の問題じゃ。 だって、《くの字》を $4$ 個横に並べたら、場所取るじゃん？　でも、 《くの字》を $4$ 個書くってゆーのは、当たってたもん！」

僕「はいはい。えっと、次のパネルは $50$ から $59$ だね」

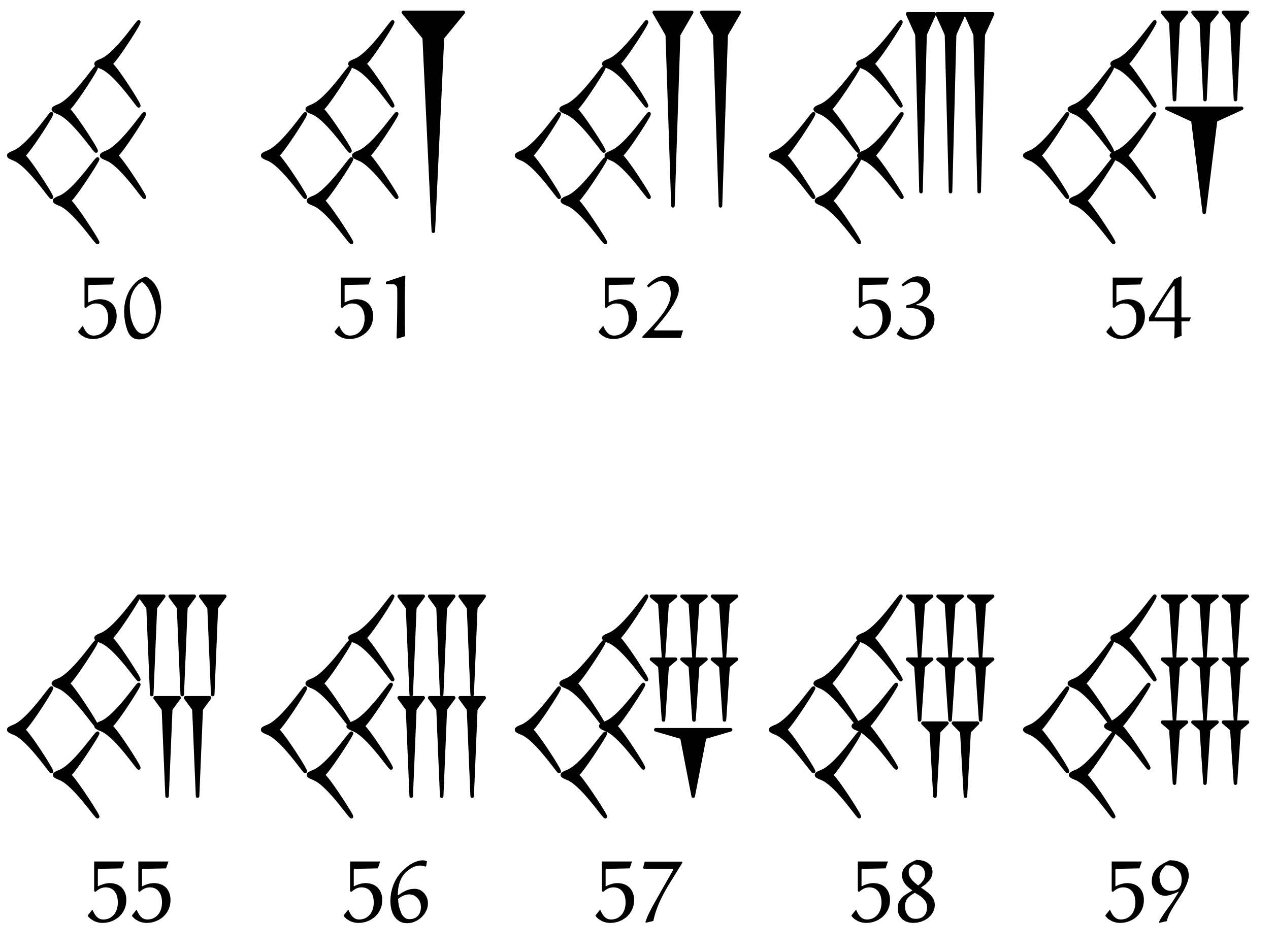
ユーリ「想像通りじゃん。次の $60$ は《くの字》が $6$ 個並ぶんでしょ、どーせ。 そろそろ飽きてきたね。バビロニアはもう十分だよ、次の部屋に行かない？」

僕「あれ？」

ユーリ「ほえ？」

僕「$60$ が縦棒 $1$ 個になってる」

ユーリ「パネル、まちがってるんじゃない？　縦棒 $1$ 個は $1$ だったじゃん。リサ姉に言っとこーよ」

僕「いや、まちがいじゃないな。だって、ほら、 $61$ と $62$ を見てごらん。 縦棒 $1$ 個がまるで $60$ であるかのように話が進んでいる。縦棒 $2$ 個を、あいだを少し空けて並べたら $61$ で、 縦棒を $1$ 個と $2$ 個並べたら、 $62$ になってるよね」

ユーリ「そーだけど？」

僕「つまり、 $$ \begin{align*} 61 &= 60 + 1 \\ 62 &= 60 + 2 \\ \end{align*} $$ のように書いているのがわかる。だから、縦棒 $1$ 個は確かに $60$ の扱いになってるんだよ」

ユーリ「そんなわけないじゃん。 $61$ や $62$ はいーけど、 $60$ と $1$ はまったく同じでしょ？　区別つかない数字なんて、そんなの、ありえない！」

僕「ほら、 $69,70,71$ のパネルも全部、同じ考え方になってるよ。左側にある縦棒は $60$ の扱いになってる」

ユーリ「ほんとだ。うーん……あれれ？　 $70 = 60 + 10$ っておかしくない？　だって、これって合わせたら $11$ にもなる」

僕「違うね。 $11$ と $70$ では順序が逆になるから」

ユーリ「むむむ……だったら、ヒエログリフと違うってこと？」

僕「そうだね。ヒエログリフでは、 $11$ と $70$ はまったく違うし、左右を逆転させても誤解は生じない。 でも、バビロニアでは、文字の場所が意味を持ってる。左右を入れ換えたら数が変わってしまう。 うん、だから、バビロニアでは僕たちが使っている数の書き方と同じように《位取り記数法》を使っているといえるね！」

ユーリ「$12$ と $21$ は違う」

僕「そういうこと。古代エジプトでは《位取り記数法》は使っていない。でも、バビロニアでは《位取り記数法》を使っている。 うん、そして、バビロニアでは《六十進法》を使っている」

ユーリ「六十進法」

僕「だって、 $59$ までは同じ書き方で進んでいて、 $60$ になったとたん繰り上がりを起こしているからね。 ほら、 $59$ から $60$ になったとたん $1$ に戻ったように見えたのは、ちょうど僕たちが $9$ から $10$ になったとたん、 上の位が $1$ になったようなものなんだ」

ユーリ「……ダウト」

僕「なぜダウト？」

ユーリ「だって、 $9$ から $10$ になったときは一の位に $0$ があるもん。だから、 $1$ と $10$ の区別付くじゃん？　でも、 バビロニアだと $1$ と $60$ の区別が付かない。そんなのなんだかおかしーよ」

僕「確かに。うーん……ともかく、パネルを進んでみようか」

ユーリ「あ、クイズだ」

僕「なるほど……」

ユーリ「$60$ で繰り上がりするから……」

僕「わかった？」

ユーリ「たぶん。こうかにゃ？」

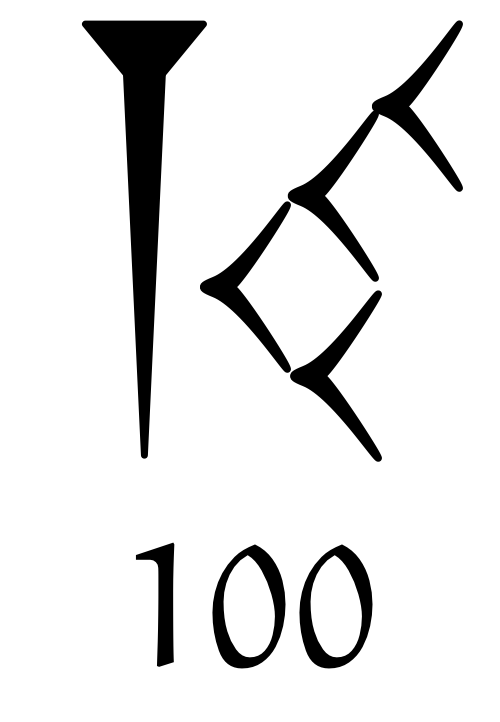
僕「そうだね」

ユーリ「よかったー。 $100 = 60 + 40$ になるんでしょ？」

僕「こっちに解説パネルがある」

ユーリ「あり？　なんで、 $$ 100 = 60 + 40 $$ じゃなくて、 $$ 1\times60^1 + 40\times60^0 $$ って書き方になってんの？」

僕「ほら、バビロニアの記数法は、やっぱり《六十進法》なんだよ。 この書き方をよく見てごらん」

ユーリ「（来たな《先生トーク》）」

僕「僕たちの《十進法》で《位取り記数法》のとき、各桁は $10$ の $n$ 乗という形になるよね。 一の位は $10^0$ で、十の位は $10^1$ で、百の位は $10^2$ で、千の位は $10^3$ になる。だから、たとえば $2017$ という数の書き方は、 $$ 2017 = 2\times10^3 + 0\times10^2 + 1\times10^1 + 7\times10^0 $$ という意味だし、 $100$ という数の書き方は、 $$ 100 = 1\times10^2 + 0\times10^1 + 0\times10^0 $$ という意味。 $10$ の $n$ 乗が基本になるのは、《十進法》だからで……」

ユーリ「わーった。わかりましたよ。だから $60$ の $n$ 乗って書けば《六十進法》ってこと。 バビロニアでは、 $$ 100 = 1\times60^1 + 40\times60^0 $$ みたいに書きますよーって？」

僕「そういうことだね。さすが、ユーリは理解が早いな」

ユーリ「ちっちっちっ。お兄ちゃんは詰めが甘いにゃ」

僕「何のこと？」

ユーリ「お兄ちゃんは、《六十進法》という思い込みがあるから、 バビロニアの記数法、しっかり見てないよね」

僕「だから、何の話？」