![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは、複素平面を使った数学トークを楽しんでいる(第163回参照)
僕「こんなふうに《複素数》を複素平面上の《点》だと考えると、 《複素数の計算》は《点の移動》として考えることができるね。 だから、計算でいろんな形を作ることができる」
ユーリ「そだね……ふよよ?」
僕「ふよよ?」
ユーリ「ちょっと待って、いまひらめいたことがある。 《複素数》を複素平面上の《点》として考えるって、 そーじゃなきゃいけないわけじゃないよね?」
僕「どういうこと?」
ユーリ「だーかーら! 《点》じゃないもので《複素数》を考えてもいーよね?」
僕「うーん、まだよくわからないけど、ユーリはどんなことを考えてるの?」
ユーリ「複素数 $a + bi$ があるでしょ? それって二つの実数じゃん?」
僕「まあそうだね。 $a$ と $b$ は実数で、だからこそ $(a,b)$ という点が複素数に対応している」
ユーリ「てことは、二つの実数を図に描けば、それは複素数になるよね?」
僕「……ごめん、お兄ちゃんには複素平面上の点しか思いつかないんだけど」
ユーリ「こーゆーの! すごくシンプル! 《線分》で表すから、名付けて《複素線分》なんちゃって」
ユーリの考えた《複素線分》
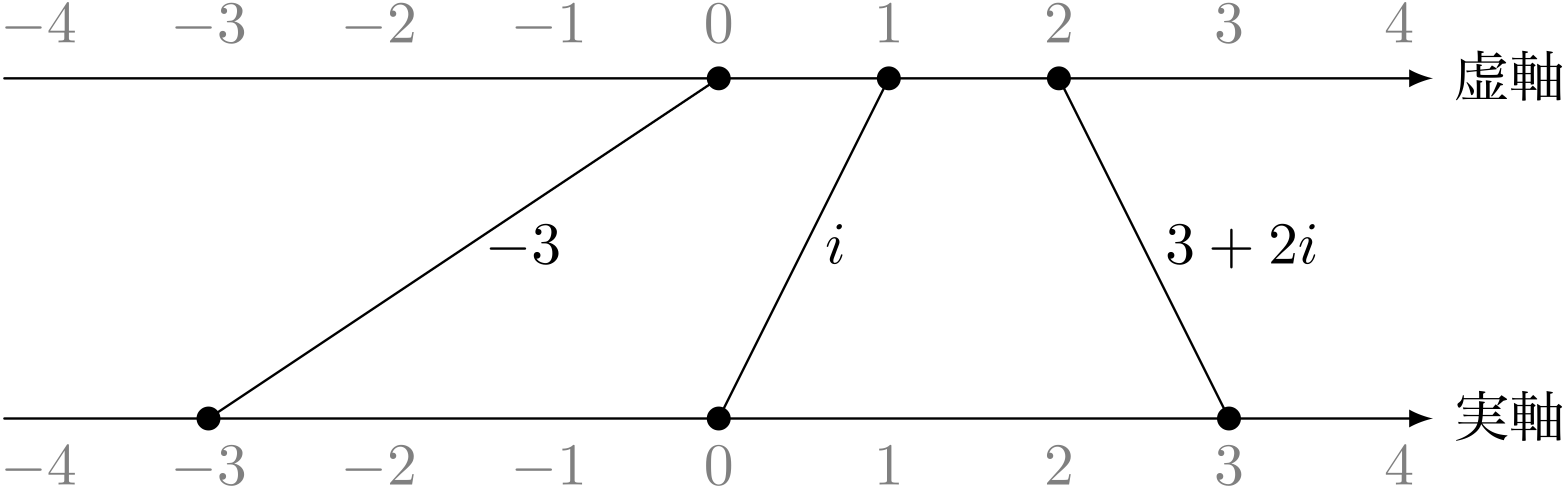
僕「ええと、これは、複素数 $a+bi$ の $a$ と $b$ を線分で結んだってことかなあ」
ユーリ「そだよ。もちろん。見ればわかるじゃん」
僕「なるほどね。確かに、これは複素数を表しているな」
ユーリ「でしょでしょ? ね、ユーリって天才? こんなの考えるなんて、将来が楽しみ?」
僕「確かに、 $a+bi$ はこの《複素線分》に対応しているから、 複素数を図で表しているといえるね。ただ……」
ユーリ「ただ? 何か文句あるの?」
僕「いや、《複素数》という数と、この《複素線分》という図とは、 どういう関係になっているのかな、って思ったんだよ。 ほら、《複素平面》の場合には、 《複素数を加える》ことは《平行移動》になっていたよね」
ユーリ「この《複素線分》だって同じだよ! だって、ほら、 $a + bi$ に $1 + i$ を足したら……ね? 平行移動してる!」
$(a + bi)+(1+i)$ を《複素線分》に図示
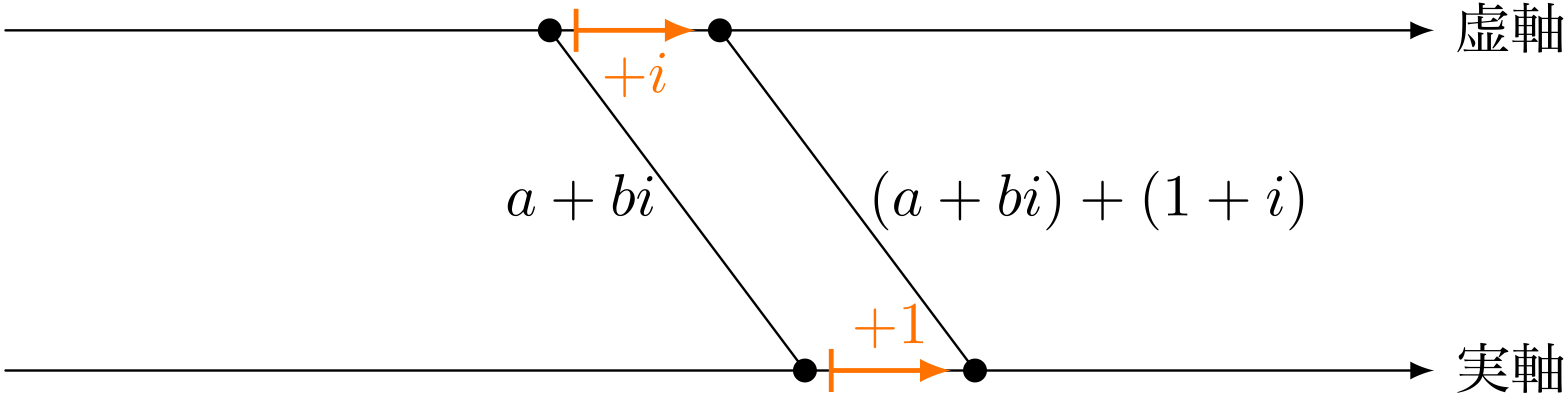
僕「なるほど……いやいや、それは違うな。それはたまたま平行移動に なっているだけだよ。《$1 + i$ を加える》っていうのは、 実部と虚部に同じ数を加えているから、たまたま平行移動になったんだ。 たとえば、 $a + bi$ に $2-i$ を足してごらんよ」
ユーリ「え……あ……そっか」
$(a + bi)+(2-i)$ を《複素線分》に図示
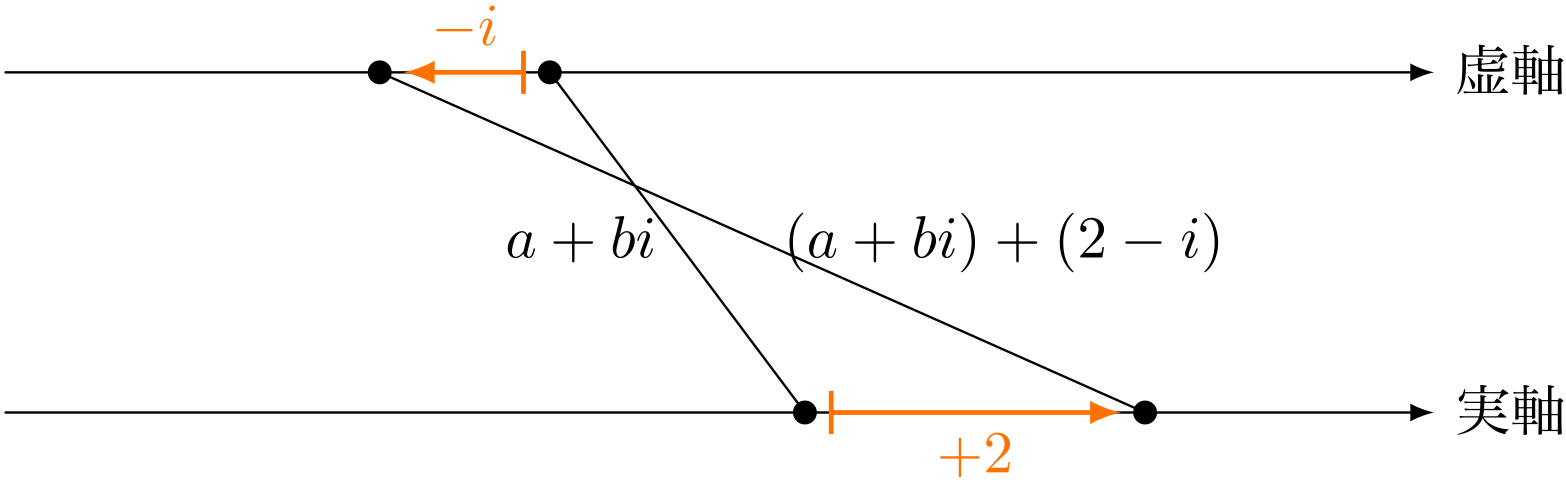
僕「確かに、ユーリが考えた《複素線分》は《複素数》を図で表しているといえる。 それはまちがいないし、すごいことだと思うよ。 でも《複素数》を《複素線分》という図で表して、 どんな意味があるのかは、よくわからないなあ……」
ユーリ「むー……そっか。図で表せばいいってもんでもないんだ」
僕「そうだね……」
ユーリ「あ、でも、《複素線分》でもいえることあるよ! たとえば、 $a + bi$ を $2$ 倍すると、 $2a + 2bi$ になるから、 《複素線分》は平行移動になる!」
僕「え? ならないよ、たとえば $1 + 2i$ を $2$ 倍したら $2+4i$ だよね」
$2(1 + 2i)$ を《複素線分》に図示
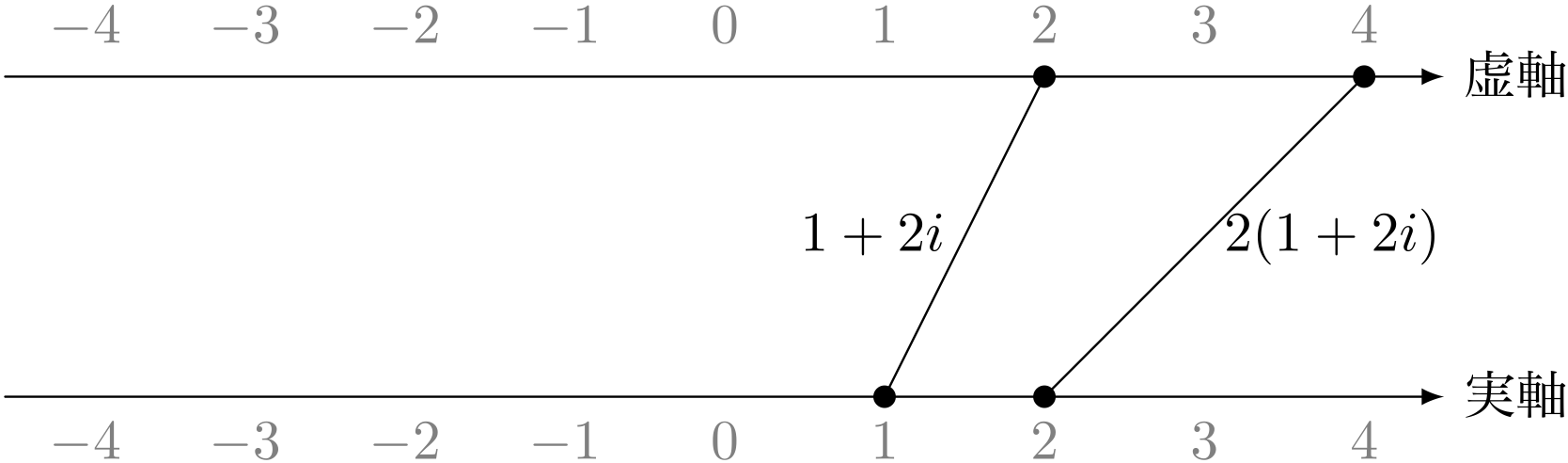
ユーリ「ありゃ。ならないか……むー」
僕「ならないね。 そう考えると、やっぱり《複素平面》というのはなかなかすぐれた表し方なんだね」
ユーリ「《複素平面》だと《$2$ 倍》ってどーなるの?
僕「考えてみればわかるよ。たとえば、 $2$ の点は $4$ に移動するし、 $-2$ の点は $-4$ に移動するよね」
ユーリ「え? あ、そだね。 $0$ の点は動かない。だから、 実数はぐわーっと広がる感じ?」
実数を $2$ 倍した様子
僕「そうそう。それから、 $2i$ の点は $4i$ に、 $-2i$ の点は $-4i$ に移動」
ユーリ「あ、わかった! $0$ を中心にして、みんなぐわーっと広がるんだ!」
複素数の点を $2$ 倍した様子(格子点)
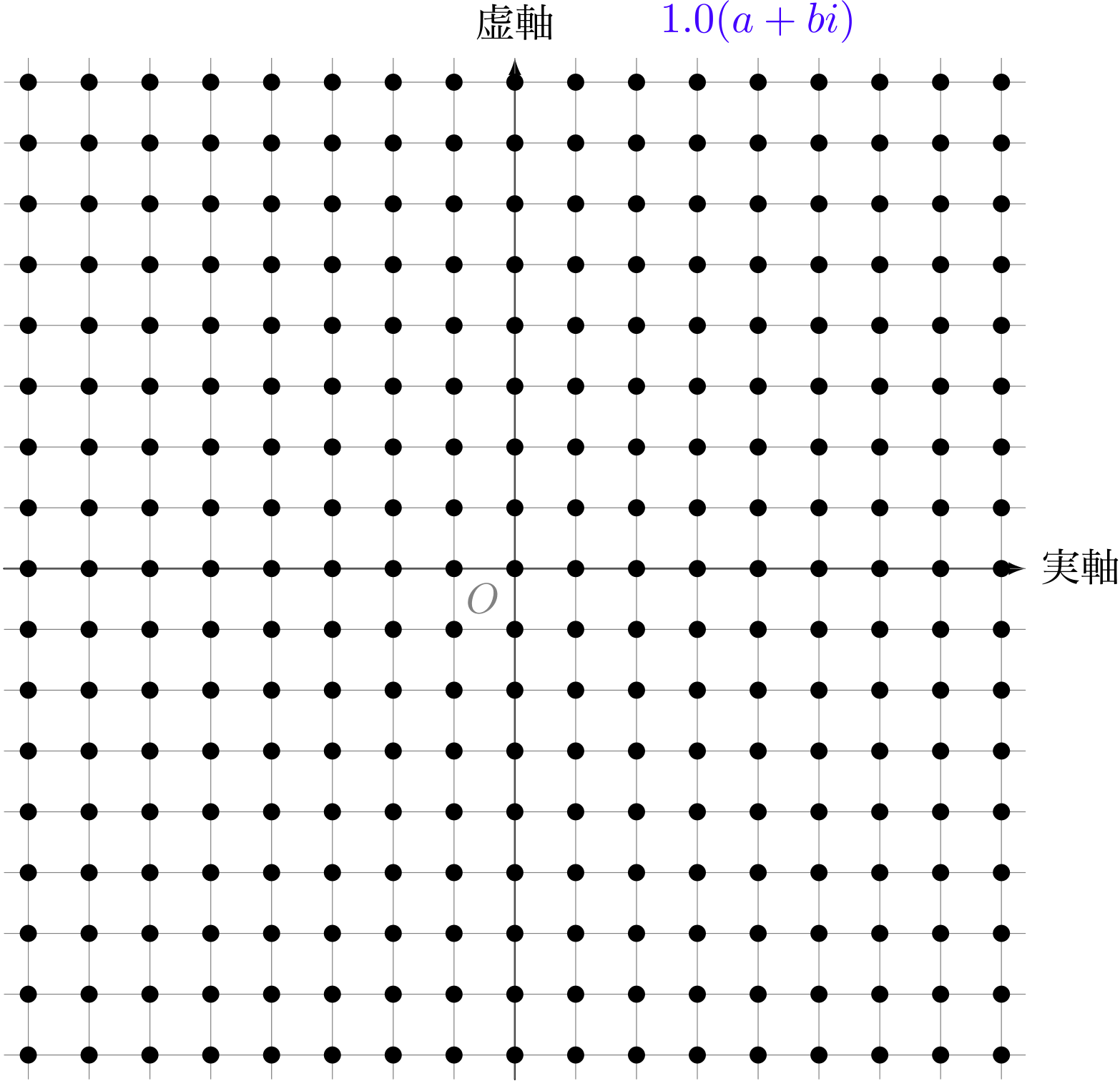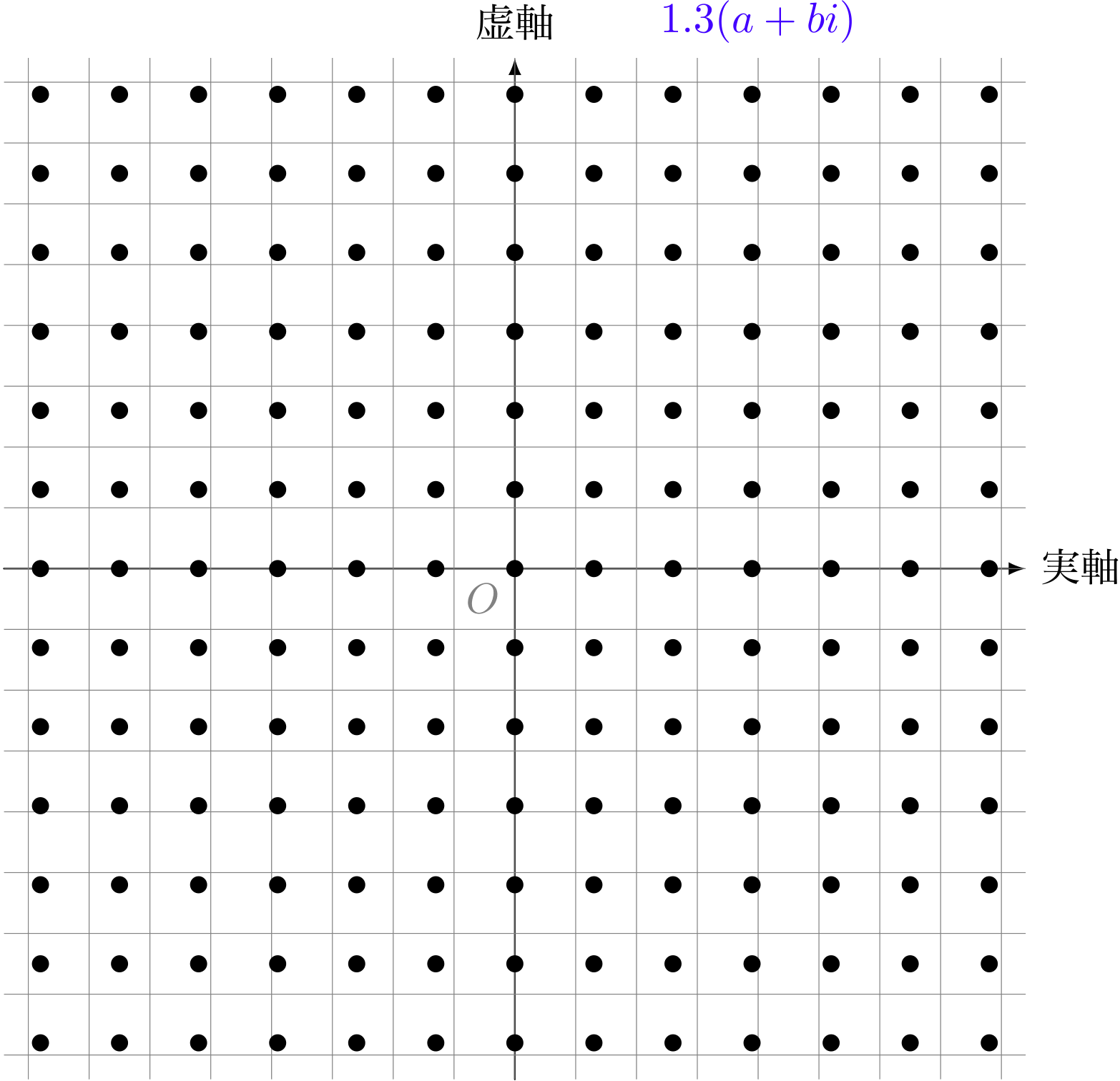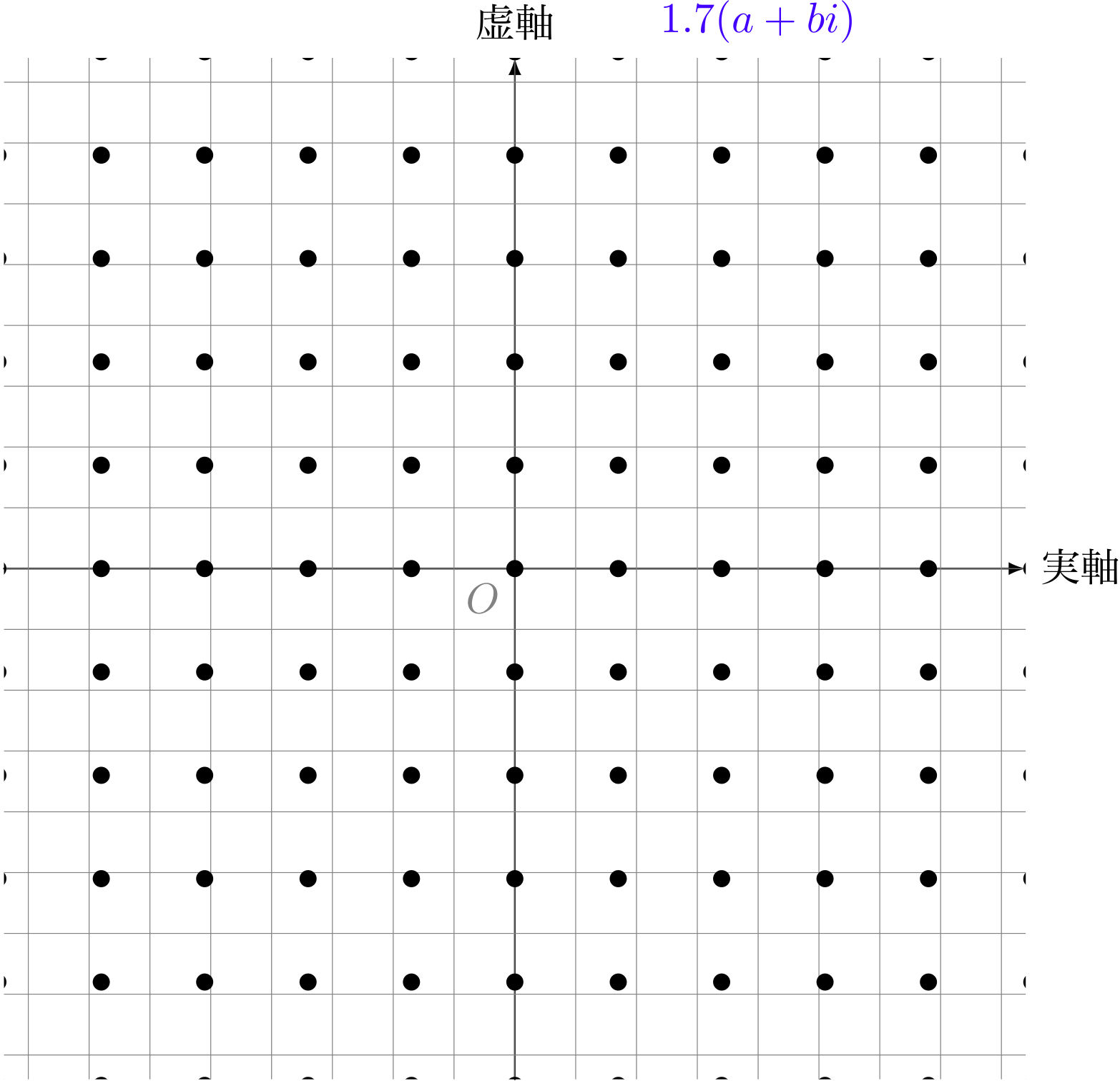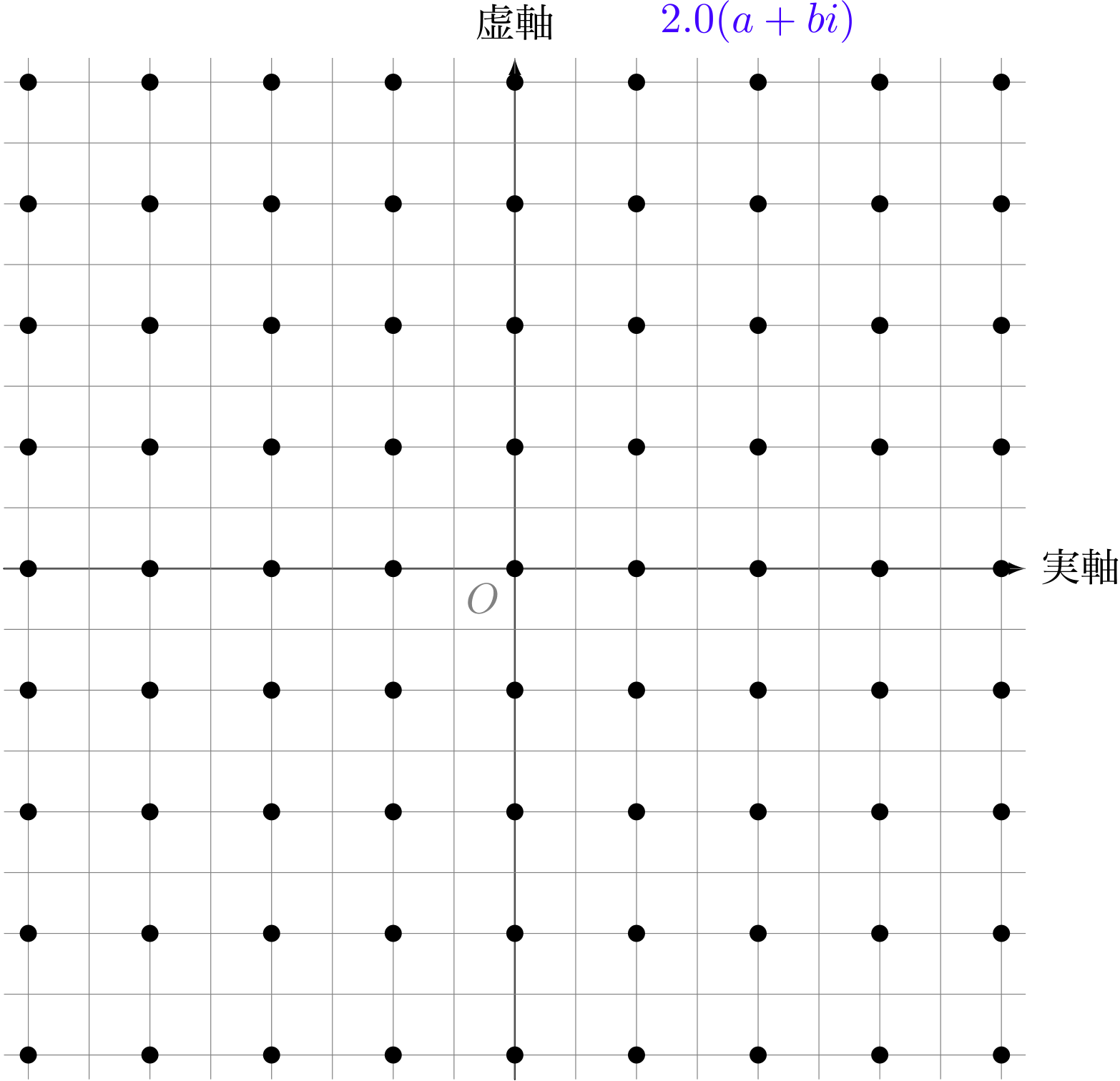
僕「そうだね。《複素数 $a+bi$ を $2$ 倍する》というのは、 《点 $(a,b)$ を $(2a,2b)$ に移す》という操作に対応する。 そしてそれは円が広がるような操作になるんだね」
複素数の点を $2$ 倍した様子(円状)
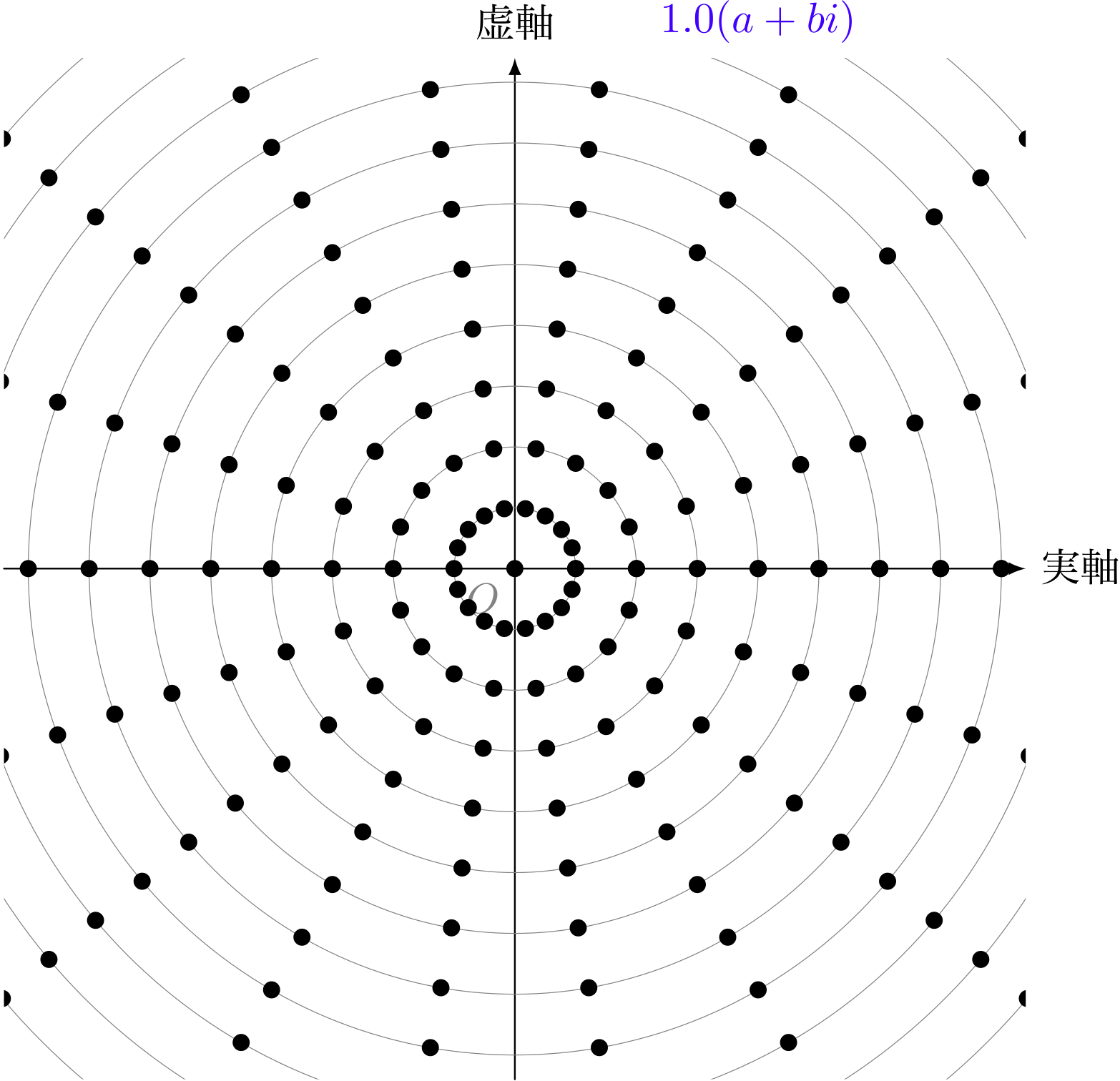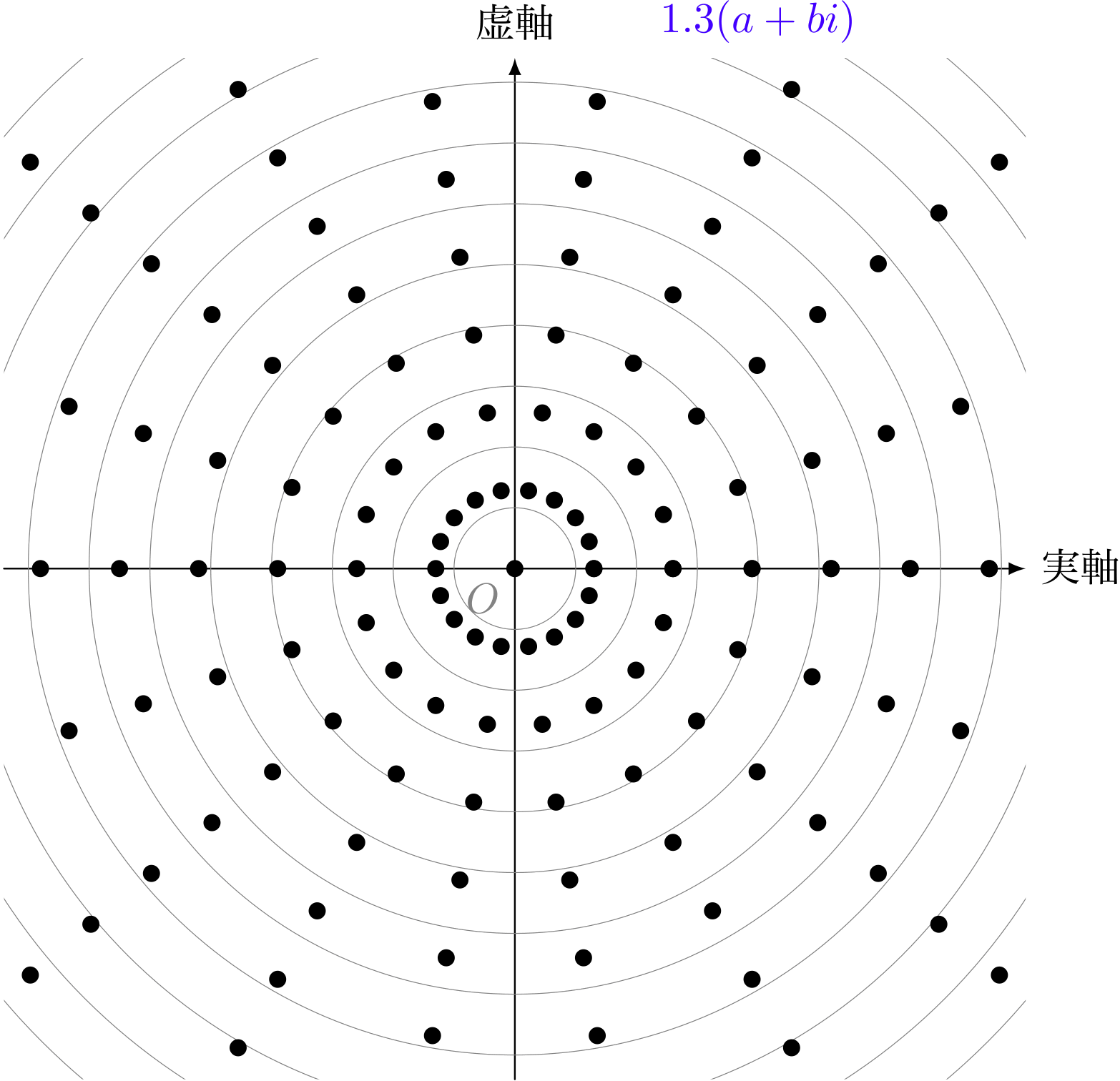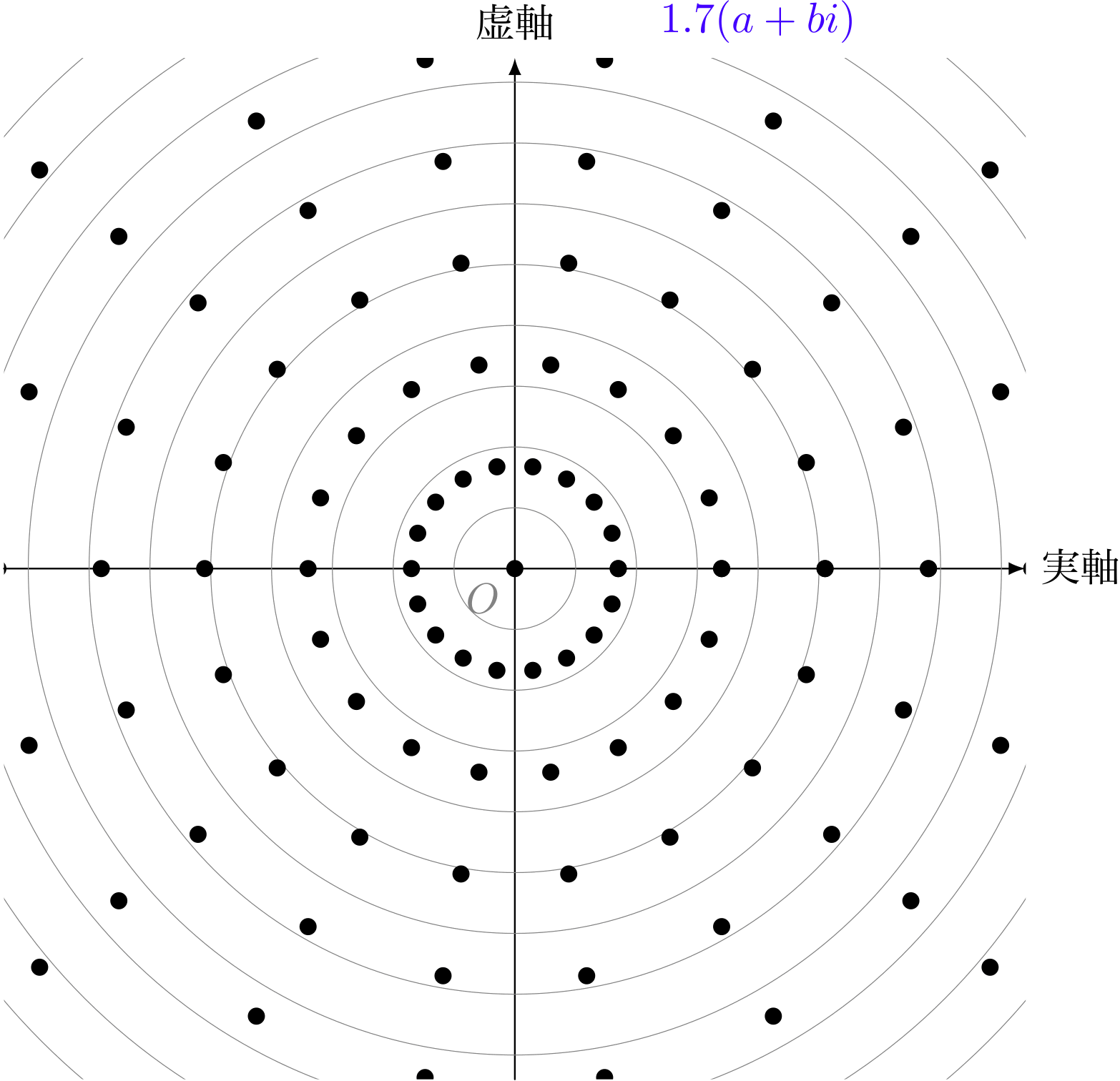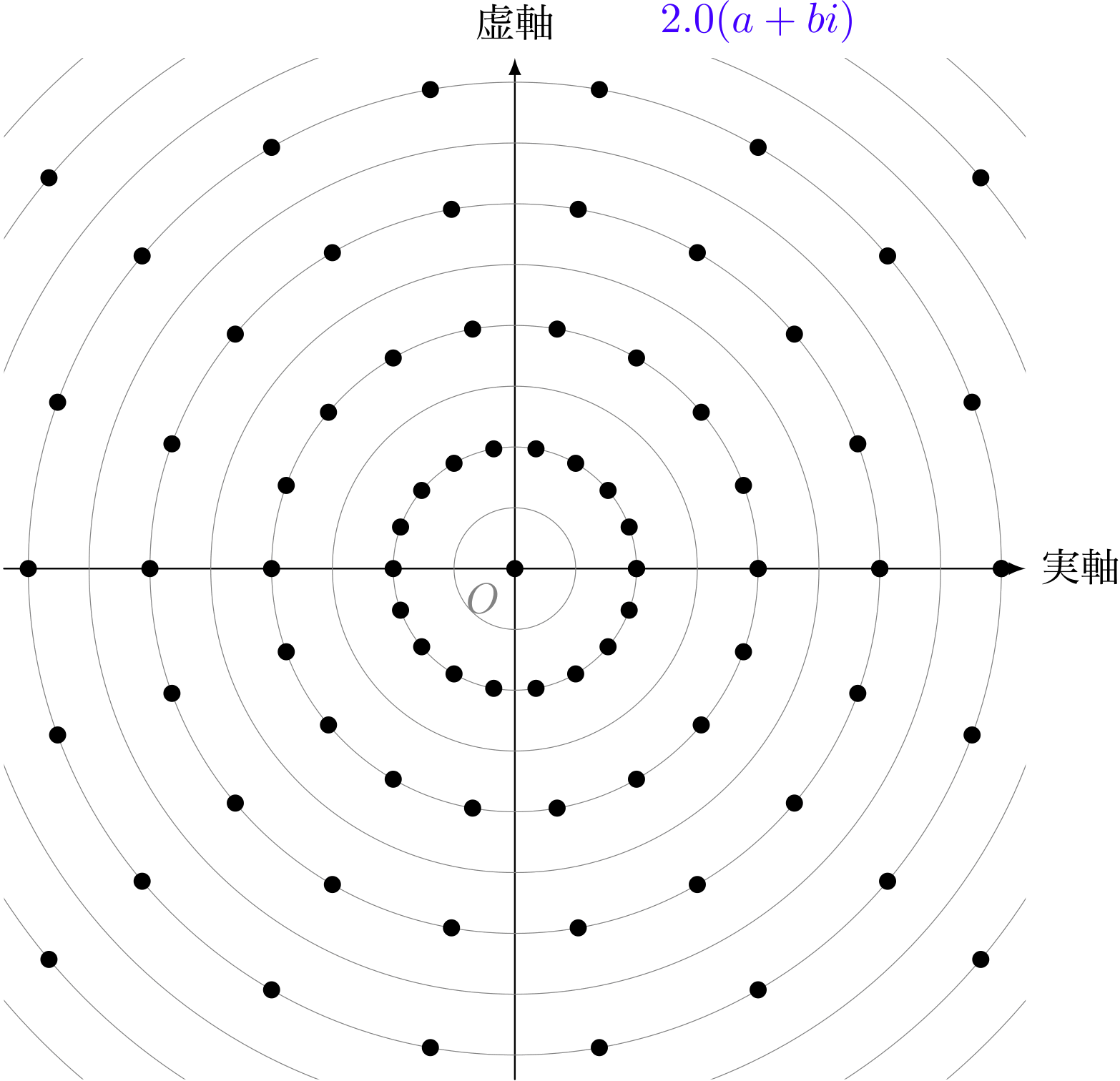
ユーリ「なーるほど! 半径が $2$ 倍?」
僕「そうだね。そしてね、 原点 $(0,0)$ と $(a,b)$ との《距離》を計算してみると、 《複素数を $2$ 倍する》と、《複素数の絶対値が $2$ 倍になる》し、 《原点からの距離も $2$ 倍になる》ことが数式で確認できるよ」
ユーリ「数式? 距離?」
僕「ほらほら、ピタゴラスの定理で説明したよね。 複素数の絶対値!」
複素数 $a + bi$ の絶対値 $\ABS{a + bi}$
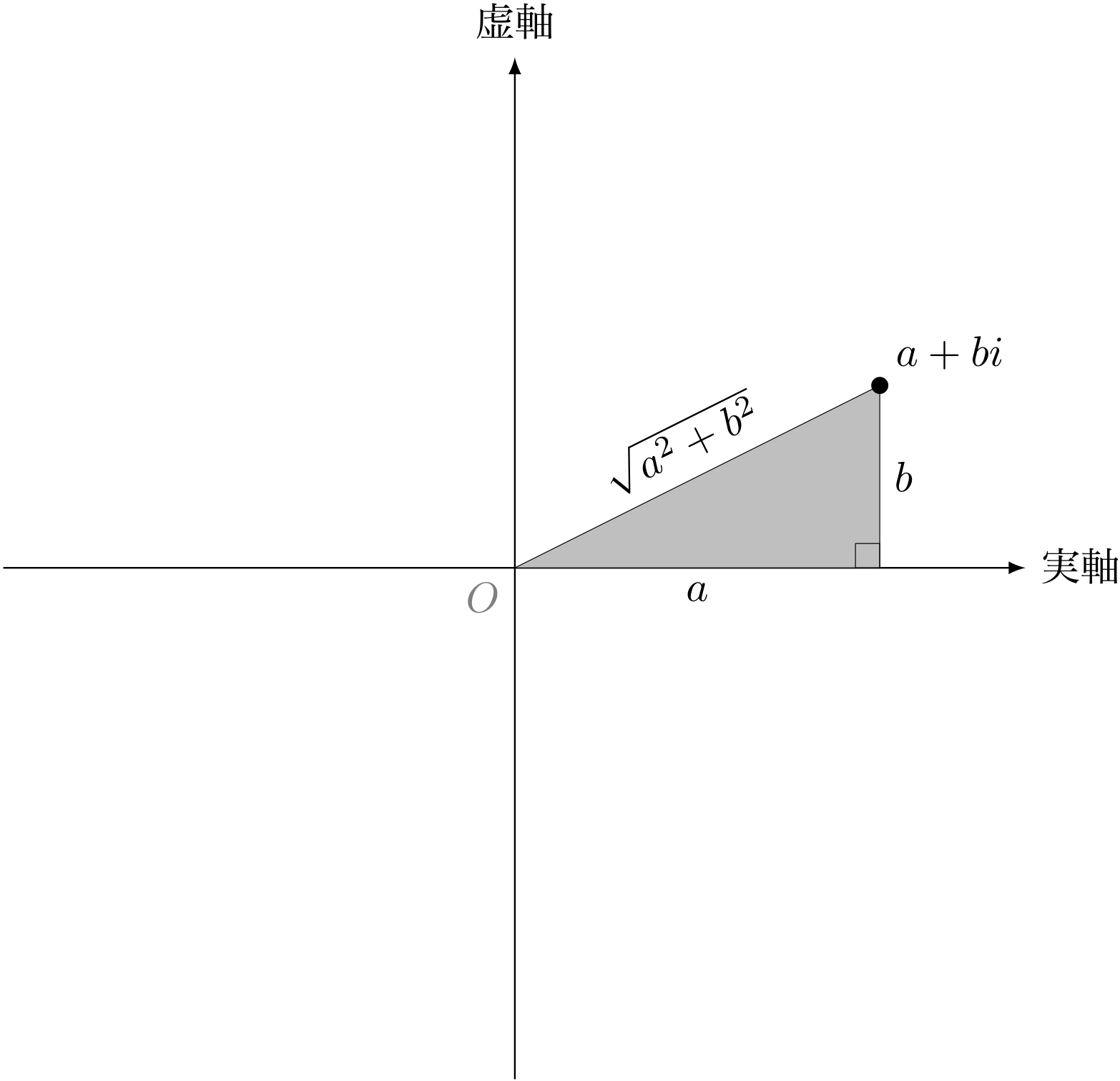
$$ \ABS{a + bi} = \sqrt{a^2 + b^2} $$
僕「$\ABS{2(a + bi)}$ が、 $\ABS{a + bi}$ のちょうど $2$ 倍になるのはかんたんに証明できるよ。 計算すればいいんだ」
$$ \begin{align*} \ABS{2(a + bi)} &= \ABS{2a + 2bi} && \REMTEXT{展開した} \\ &= \sqrt{(2a)^2 + (2b)^2} && \REMTEXT{絶対値の定義にあてはめた} \\ &= \sqrt{4a^2 + 4b^2} && \REMTEXT{カッコをはずした} \\ &= \sqrt{4(a^2 + b^2)} && \REMTEXT{$4$でくくった} \\ &= \sqrt{2^2 (a^2 + b^2)} && \REMTEXT{$2^2 = 4$だから(ルートの外に$2$を出す準備)} \\ &= 2\sqrt{a^2 + b^2} && \REMTEXT{ルートの外に$2$を出した} \\ &= 2\ABS{a + bi} && \REMTEXT{絶対値の定義にあてはめた} \\ \end{align*} $$ユーリ「なーるほど……」
僕「だから、 $$ \ABS{2(a + bi)} = 2\ABS{a + bi} $$ が証明できた」
ユーリ「お兄ちゃんって、こういうとき数式出すの好きだよね。 さすが《数式マニア》の二つ名はダテじゃないにゃ」
僕「その二つ名を口に出すのユーリだけだよ、言っとくけど。 それにこれはマニアってほどじゃない計算だし」
ユーリ「そーなんだ」
僕「だって、証明したいことは $\ABS{2(a+bi)} = 2\ABS{a+bi}$ なんだから、何とかして $2$ をくくり出せ!という方針がはっきりしてる」
ユーリ「そっか」
僕「ともかく、 $a$ と $b$ という文字を使って計算したから、 複素平面のどんな点に対しても $\ABS{2(a+bi)} = 2\ABS{a+bi}$ がいえると断言できる。 数式はそこがいいんだよ。たった一言で《すべて》を扱えるんだから。 文字を使えば一般化して議論ができる」
ユーリ「はいはいはい、熱弁だにゃあ。 ところでね、いま $2$ と書いたところも《いっぱんか》できるの?」
僕「それはすばらしい指摘だな! そうだね……うん、じゃ、これを証明するのかな?」
問題(?)
$a, b, r$ を実数とする。このとき、以下の式が成り立つことを証明せよ。 $$ \ABS{r(a + bi)} = r\ABS{a + bi} \qquad \REMTEXT{(?)} $$
ユーリ「そだね……あり? おかしくない?」
僕「なにがおかしいのかな」
ユーリ「だってね、 $r = -2$ のとき、変なことになるもん」
僕「よく気付くなあ。そうだね。 さっきの式はすべての実数 $r$ で成り立つとは限らない。 $r \geqq 0$ という条件が必要になるね」
問題
$a, b$ を実数とし、 $r$ を $0$ 以上の実数とする。このとき、以下の式が成り立つことを証明せよ。 $$ \ABS{r(a + bi)} = r\ABS{a + bi} $$
ユーリ「これ、さっきと同じ計算すればいーってことだよね」
$$ \begin{align*} \ABS{r(a + bi)} &= \ABS{ra + rbi} \\ &= \sqrt{(ra)^2 + (rb)^2} \\ &= \sqrt{r^2a^2 + r^2b^2} \\ &= \sqrt{r^2(a^2 + b^2)} \\ &= r\sqrt{a^2 + b^2} \\ &= r\ABS{a + bi} \end{align*} $$僕「そうだね。そして、 $\sqrt{r^2(a^2 + b^2)} = r\sqrt{a^2 + b^2}$ のところで、 $r \geqq 0$ を使ったことになる。 実数 $r$ を $2$ 乗してルートを取ったときに元に戻るのは、 $r \geqq 0$ のときだけだから。 $r < 0$ ならマイナスを付ける必要が出る」
実数 $r$ を $2$ 乗して、ルートを取ったらどうなるか
$r \geqq 0$ のとき、 $$ \sqrt{r^2} = r $$ が成り立つ。
$r < 0$ のとき、 $$ \sqrt{r^2} = -r $$ が成り立つ。
ユーリ「これ、さっきお兄ちゃんが言ってた話じゃん」
僕「そうだっけ」
ユーリ「これって、 $r$ の《絶対値》ってことだよね!」
実数 $r$ を $2$ 乗して、ルートを取ると絶対値になる
$$ \sqrt{r^2} = \ABS{r} $$
僕「おっと、そうだね、その通り! だから《$r$ 倍した複素数の絶対値》は、 《複素数の絶対値の $\ABS{r}$ 倍》といえる」
$r$ 倍した複素数の絶対値は、複素数の絶対値の $\ABS{r}$ 倍
$$ \ABS{r(a+bi)} = \ABS{r}\,\ABS{a + bi} $$
ユーリ「ねーお兄ちゃん。絶対値って《大きさ》みたいなもの?」
僕「まあ、そうだね。ある意味では複素数の《大きさ》みたいなものだね。 絶対値は必ず $0$ 以上になる。マイナスにはならない」
ユーリ「実数でも複素数でもそうだよね。絶対値」
僕「そうそう、そうなるね。さっき(第163回)も話したけど、 複素数の絶対値の定義は、実数の絶対値とうまく合っている。 複素数 $a+bi$ で $b = 0$ にしたときにはちょうど実数の絶対値の定義になっているから」
$b = 0$ のとき、 $\ABS{a+bi} = \ABS{a}$ になる $$ \ABS{a+0i} = \sqrt{a^2+0^2} = \sqrt{a^2} = \ABS{a} $$
ユーリ「でね、でね、 《大きさ》は絶対値ってわかったけど、《向き》はどこにあるの?」
僕「《向き》はどこにあるか?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年7月29日)
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!