![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
僕とユーリは《数を $2$ 乗する》という数学トークを続けている(第161回参照)。
僕「今度は、 $b$ から反対にたどってみよう」
グラフを利用して、 $b$ の点から $-\sqrt{b}$ と $\sqrt{b}$ を得る
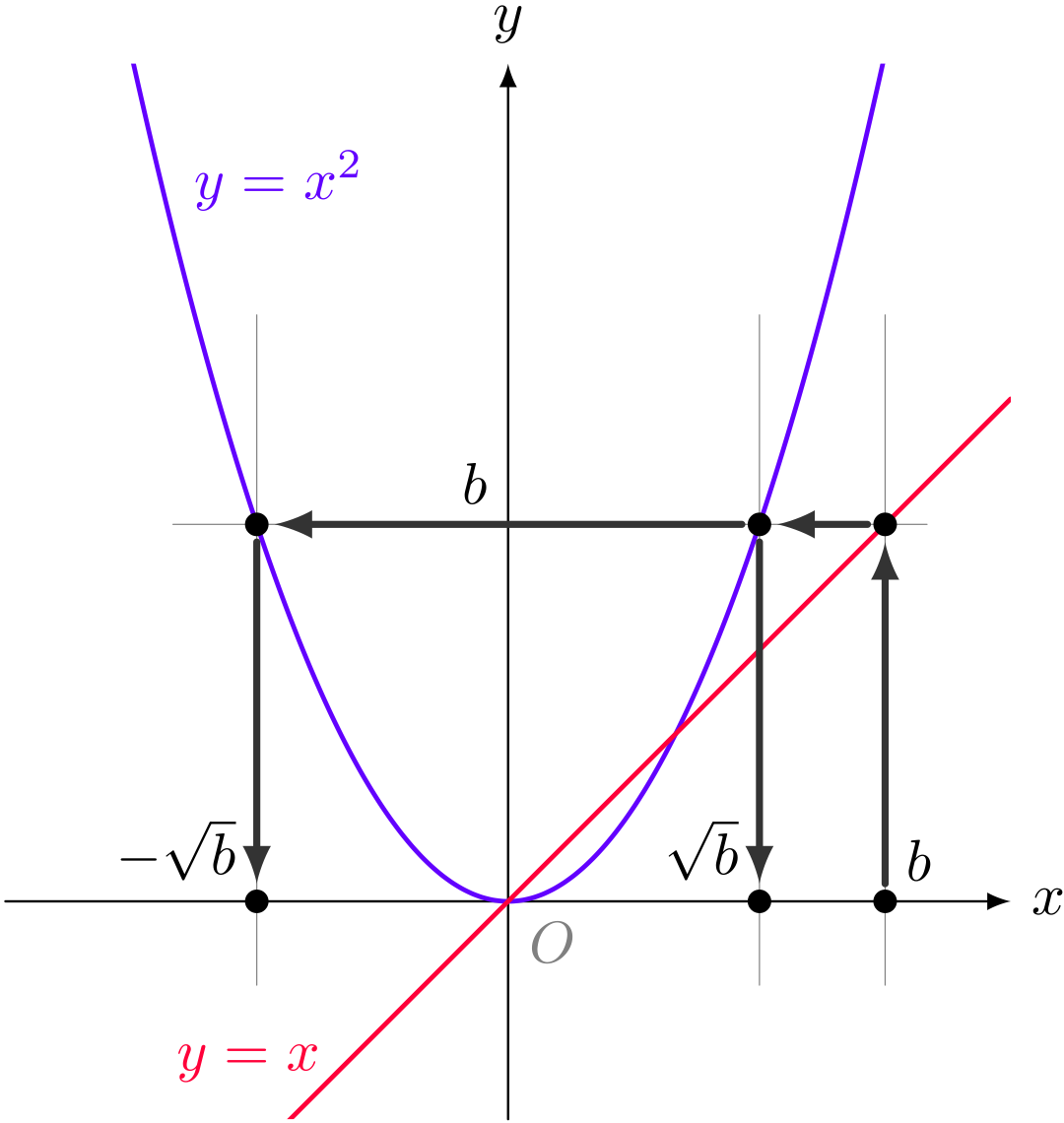
ユーリ「$9$ から始めたら、 $-3$ と $3$ に戻ってくる?」
僕「そういうことになる。 $-\sqrt{9} = -3$ で $\sqrt{9} = 3$ だからね。ちゃんと $2$ つの答えが出てくる。 数を $2$ 乗するときに起きることが、 こんなふうにグラフに現れてくるのは楽しいね!」
ユーリ「そっか……数式とグラフは関係してる?」
僕「もちろんだよ、ユーリ。数式 $y = x^2$ で表したものも、 いま描いたグラフで表したものも、おおもとは同じだからね」
ユーリ「おおもと」
僕「うん、だから、 《数を $2$ 乗したらどういう数になるか》という対応関係を表している」
ユーリ「$3$ を $2$ 乗したら $9$ になるとか?」
僕「そういうこと。《ある数 $x$》に対して、 《$x$ を $2$ 乗した数》が、《たった一つ》決まる。 こういう対応関係を関数(かんすう)っていうんだよ。この対応関係は関数の例になる」
関数の例
$$ \REMTEXT{《ある数$x$》} \longmapsto \REMTEXT{《$x$を$2$乗した数》} $$
ユーリ「んー、あたりまえすぎて、何いってるかわかんない」
僕「あたりまえの話じゃないよ。たとえば、そうだなあ…… 《$0$ 以上の数 $y$》に対して、 《$2$ 乗したら $y$ になる数》を対応させる。 こういうのは関数とはいわない。どうしてだかわかる?」
ユーリ「へ? それ、関数じゃないの?」
関数にはならない例
$$ \REMTEXT{《$0$以上の数$y$》} \longmapsto \REMTEXT{《$2$乗したら$y$になる数》} $$
僕「そうだね。普通はいわない。どうしてかというと……」
ユーリ「待って! さっきのお兄ちゃんの《先生トーク》によると……」
僕「探り入れるなって」
ユーリ「そっか、《たった一つ》じゃないから? たとえば、 $y = 9$ だと、 $3$ でも $-3$ でもいいわけじゃん? 《たった一つ》といえないから関数じゃない?」
僕「そういうことだね。 $9$ という数が与えられたとき、 《$2$ 乗したら $9$ になる数》は《たった一つ》に決まらない。 だから、この対応関係は関数とはいわない。 それは関数という数学用語の約束」
ユーリ「ダウト! それおかしーよ。だって、 《$3$ と $-3$ という数の組》は《たった一つ》に決まるもん!」
僕「ユーリは賢いなあ! それは高度な指摘だね。 さっきはかんたんに言っちゃったけど、正確に《関数》という言葉を使うときには、 《どんな集合の要素》から《どんな集合の要素》への対応関係なのかをはっきりさせなくちゃいけないんだ。 さっきお兄ちゃんは、《$0$ 以上の数》から《実数》への対応関係のつもりで言った。 ユーリが言うように、数の組を考えたいときには、また別の話になる。でも、ユーリの指摘は鋭い」
ユーリ「《数の組》としては《たった一つ》に決まるけど、《数》としては《たった一つ》に決まらないから……ってこと?」
僕「そうだね。いま話した《関数かどうか》という話は、 これも、 $y = x^2$ のグラフから読み取れる。 たとえば、 $y = x^2$ で《$x$ を決めたら $y$ がたった一つ決まる》というのは、 《垂直線と $y = x^2$ との交点は必ず一点になる》ことに現れている」
《垂直線と $y = x^2$ との交点は必ず一点になる》

ユーリ「そかそか。 てことは《$y$ を決めても $x$ はたった一つに決まらない》 という方は、《水平線と $y = x^2$ との交点は二点になる》ことに現れている?」
僕「そうだね。 $x = y = 0$ の点を除いたらそういえる。 《$y$ を決めても $x$ はたった一つに決まるとは限らない》や、 《水平線と $y = x^2$ との交点は一点になるとは限らない》といった方が正確だね」
《水平線と $y = x^2$ との交点は一点になるとは限らない》
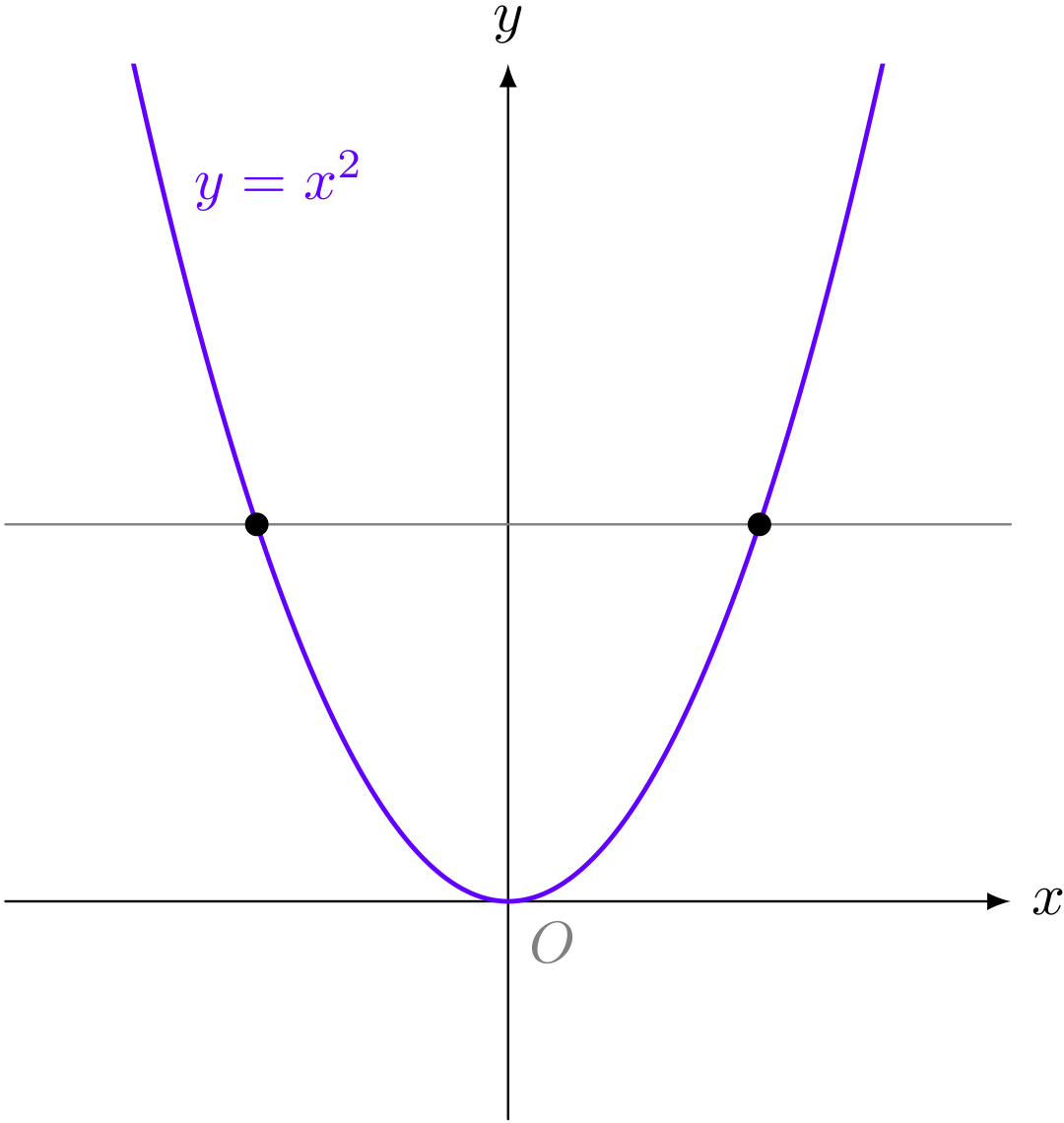
ユーリ「《とは、かぎらにゃい》」
僕「そうだね。そしてその唯一の例外、つまり水平線と $y = x^2$ の交点が一点になるときというのは、 ちょうど、放物線と水平線が一点を共有するとき。 つまり、水平線として $x$ 軸を考えるときになる」
《$x$ 軸と、 $y = x^2$ との交点は一点になる》
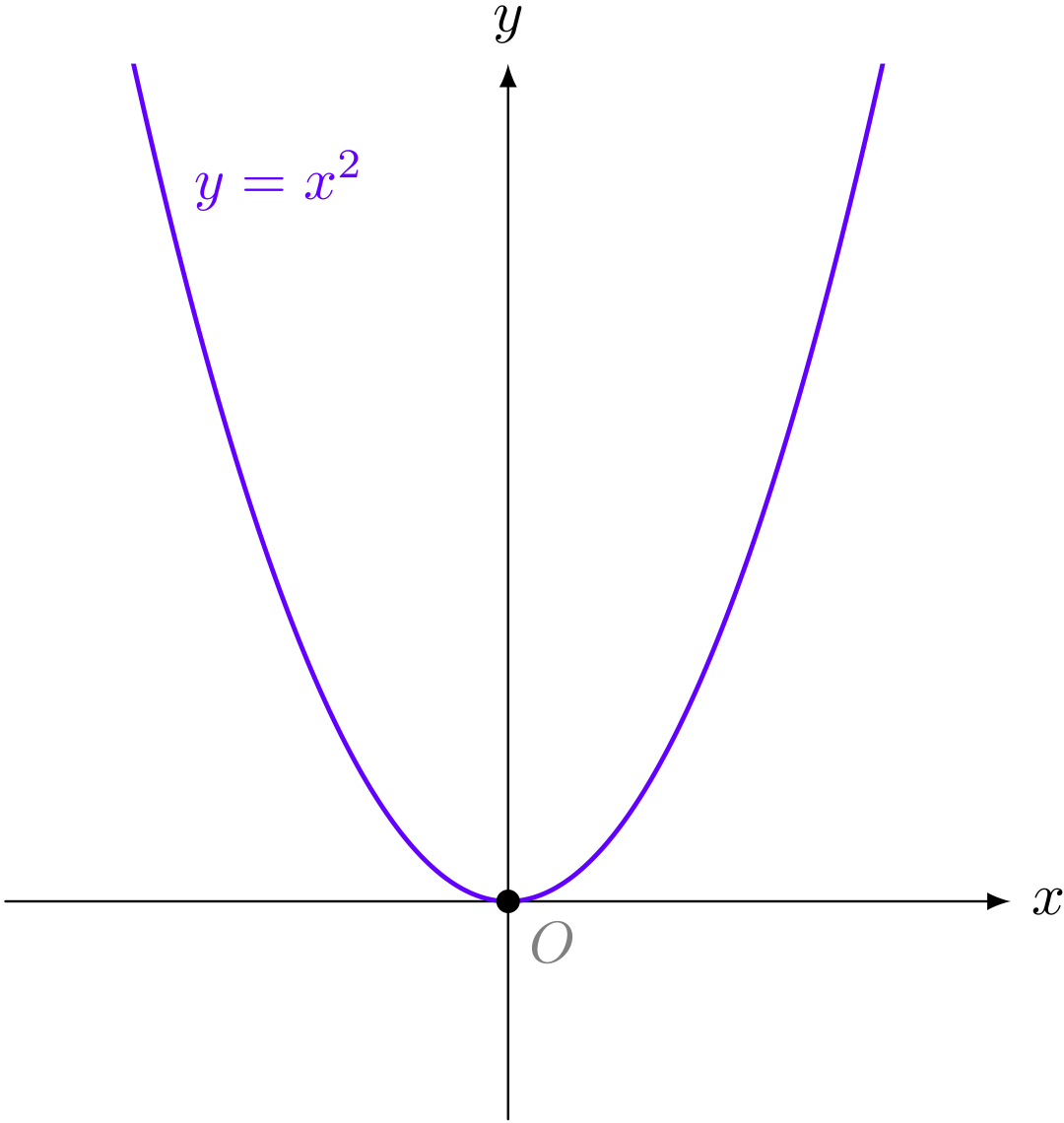
僕「交点を考えると楽しくなるよ。 《$2$ 次関数のグラフと $x$ 軸との交点》と、 《$2$ 次方程式の解》の話だね。いいかいユーリ、まずね……」
ユーリ「お兄ちゃん、お兄ちゃん。 そんなに、さっさかさっさか話を進めないでよ。 知ってた? おにーちゃんは、 コーフンすると無口か早口のどっちかになるんだから」
僕「ごめんごめん。順序立てて、具体的に話をするよ。 $2$ 次関数として、 $$ y = x^2 - 4 $$ というものを考えると、このグラフはこんな放物線になる」
$y = x^2 - 4$ のグラフ

ユーリ「ふんふん? それで?」
僕「それでね、これとは別に、 $2$ 次方程式として、 $$ x^2 - 4 = 0 $$ というものを考えると、この解は $x = 2$ と $x = -2$ になるよね」
ユーリ「いーよ。 $2^2 - 4$ も $(-2)^2 - 4$ も $0$ だから?」
僕「そうそう。そして、この $x = 2$ と $x = -2$ はちょうど、 さっきの放物線と $x$ 軸との交点になるんだ!」
《$2$ 次関数 $y = x^2 - 4$ と $x$ 軸の交点》 《$2$ 次方程式 $x^2 - 4 = 0$ の解》
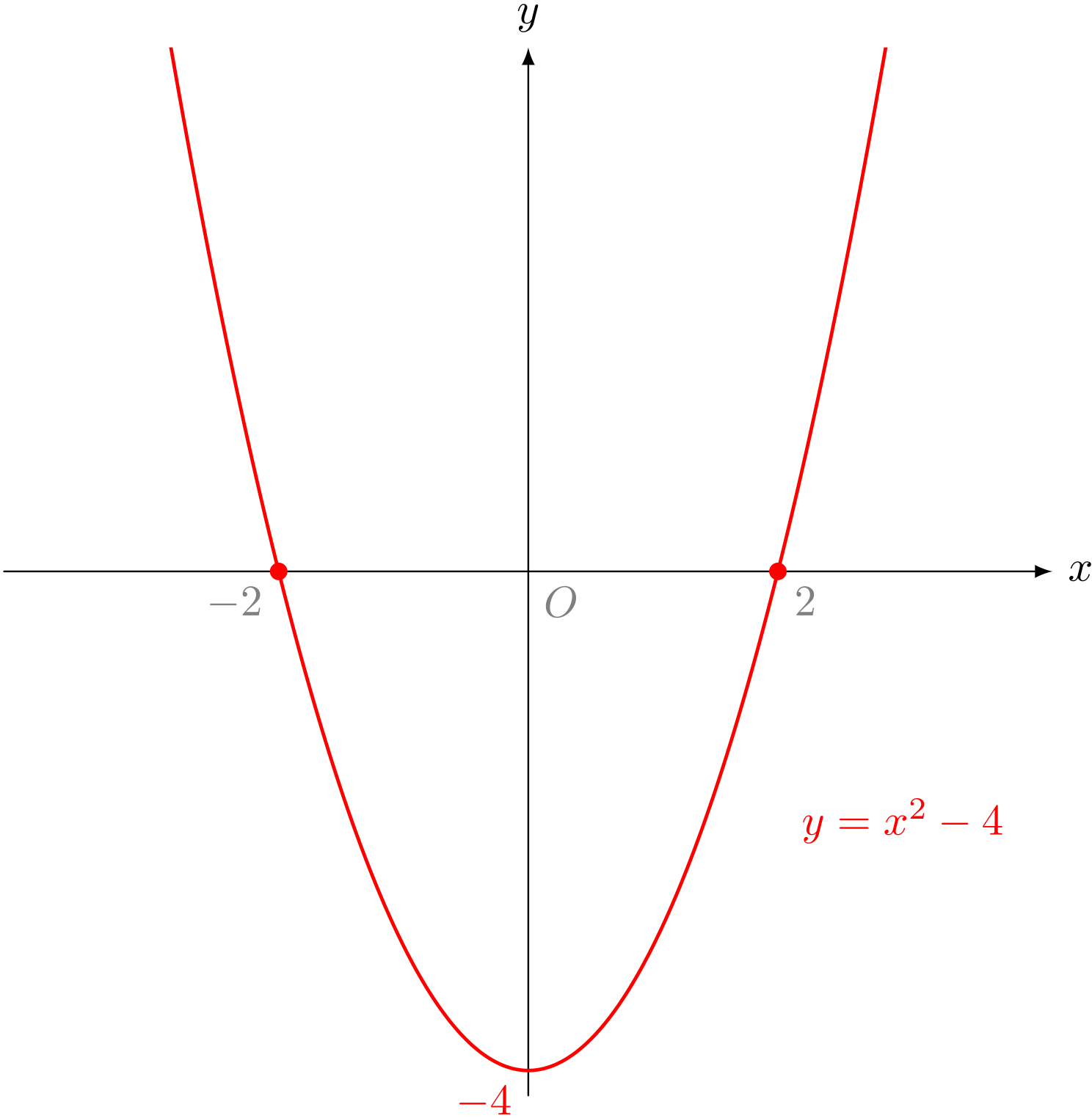
ユーリ「ほほー! ……って、それは連立方程式を解いたから、 あたりまえなのでは」
僕「そうなんだけど、話はここから。この放物線をすうっと持ち上げていく」
ユーリ「持ち上げるって、動かすってこと?」
僕「そうだよ。さっきは、 $y = x^2 - 4$ という放物線だったから、 この $4$ の部分をたとえば $1$ に変えてみる。 そして今度は $x^2 - 1 = 0$ を解くと、解となっている $x = 1$ と $x = -1$ が交点になるよね」
《$2$ 次関数 $y = x^2 - 1$ と $x$ 軸の交点》 《$2$ 次方程式 $x^2 - 1 = 0$ の解》

僕「$x^2 - 4 = 0$ や $x^2 - 1 = 0$ という数式だけを見ても解くことはできるんだけど、 いまのようにグラフを想像してみると、 放物線をすうっと上げると二つの解がすうっと動く様子がはっきりわかるだろ?」
ユーリ「ほほー! 確かにそーだね。もっと上げてもいーよね?」
僕「もちろん、いいよ。たとえば……」
ユーリ「どーせ次の例は $y = x^2$ でしょ?」
僕「先を読むなって」
《$2$ 次関数 $y = x^2$ と $x$ 軸の交点》 《$2$ 次方程式 $x^2 = 0$ の解》

ユーリ「そっか、これは解が $x = 0$ 一つ?」
僕「そうだね。 $y = x^2$ は $x$ 軸に接していて、共有する点は一点。 そしてそのとき、 $x^2 = 0$ の解も $x = 0$ だけになる」
ユーリ「……」
僕「ここまで、 $4, 1, 0$ と動かしてきた数を $A$ という文字で表すとすると、
ユーリ「$A = -1$ なら?」
僕「え?」
ユーリ「$y = x^2 + 1$ だと、交点は $0$ 個になるよね? だって、《ふわりん》と浮かぶもん」
$y = x^2 + 1$ のグラフ
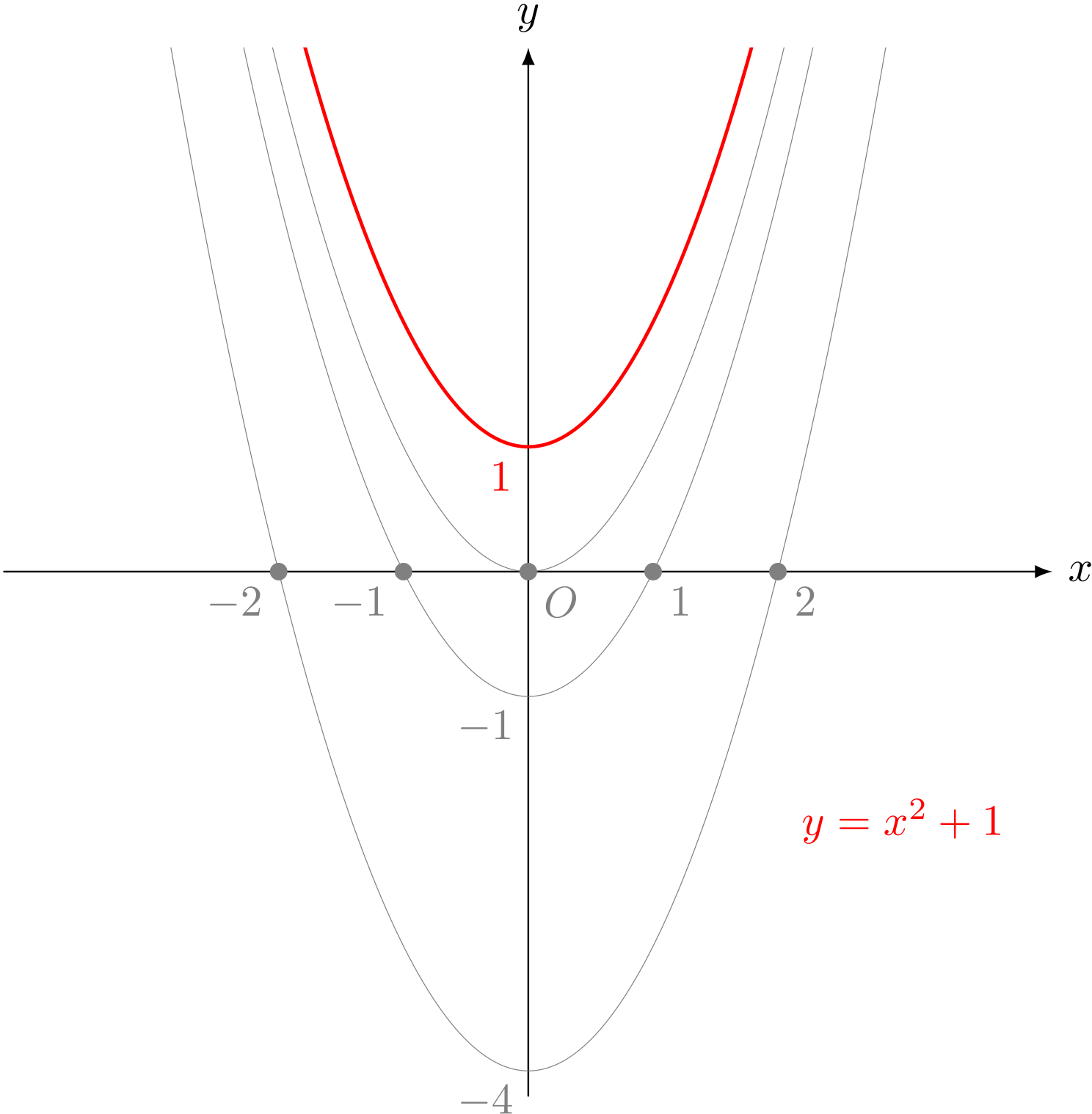
僕「うん、そうだね。だからそのときは《実数解の個数は $0$ 個》 ということになるわけだ。《実数解なし》ともいうね」
$y = x^2 - A$ で $A$ を動かしたときの動画
ユーリ「むむ? $x^2 + 1 = 0$ で $0$ 個……ダウト!」
僕「え?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年7月15日)
この記事は『数学ガールの秘密ノート/複素数の広がり』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!