第161回 シーズン17 エピソード1

2乗の広がり（前編） ただいま無料

僕の部屋

ユーリ「ねえ、お兄ちゃん。おもしろいクイズないの？」

僕「もう飽きたのか、早いなあ」

ユーリ「だって、最近あたらしい本増えてないじゃん。 もう全部読んじゃったよ」

僕「さすがに、そんなことはないだろ？」

ユーリ「読みたい本は全部読んじゃったってこと。 残っているのは読みたくない本だから、意味ないのー！　 ねー、おもしろいクイズない？　ややこしー数式が出てこなくて、 でも単純じゃなくて、引っ掛け問題でもなくて、 わくわくするクイズ」

僕「ハードルいきなり上げるなよ。じゃ、こういうクイズは？」

ユーリ「……ねー、お兄ちゃん。 ユーリはちゃんと《単純じゃなくて》っていったよね！」

僕「単純すぎた？」

ユーリ「あったりまえじゃん。 $2$ 乗すると $9$ になるのって、 $3$ と $-3$ でしょ？」

僕「そうだね。正解！　よく $-3$ を忘れなかったね！」

$$ \begin{align*} 3^2 &= 3 \times 3 = 9 \\ (-3)^2 &= (-3) \times (-3) = 9 \\ \end{align*} $$

ユーリ「あんまりホメられた感じがしない。簡単すぎるもん」

僕「じゃ、もっと難しくしようか」

ユーリ「$2$ 乗して $16$ になるのは $4$ と $-4$ だし、 $2$ 乗して $25$ になるのは $5$ と $-5$ だよ。 その系列はやめてね」

僕「話を先取りするなよ……それじゃ、こういうクイズは？」

ユーリ「簡単、簡単！　 $1$ だね。 $1^2 = 1$ で変わらないから」

僕「ほんとう？」

ユーリ「む。その《先生トーク》はユーリがまちがっているってことだ！」

僕「探り入れるなよ」

ユーリ「わかった。 $1$ だけじゃないや、 $0$ もだ。 $0^2 = 0$ で変わらない」

僕「そうだね」

$$ \begin{align*} 0^2 &= 0 \times 0 = 0 && \REMTEXT{$0$を$2$乗しても変わらない} \\ 1^2 &= 1 \times 1 = 1 && \REMTEXT{$1$を$2$乗しても変わらない} \\ \end{align*} $$

ユーリ「ま、ちょっとしたまちがいは誰にでもあるもんだよ」

僕「それを自分で言うのか。ところで、 $0$ と $1$ 以外にあると思う？」

ユーリ「何が？」

僕「だから、 $2$ 乗しても変わらない数だよ。 確かに $0$ は $2$ 乗しても値が $0$ のままで変わらないし、 $1$ は $2$ 乗しても値が $1$ のままで変わらないよね」

ユーリ「うん、 $2$ 乗してみればわかるじゃん」

僕「でも、 $0$ と $1$ 以外に、そういう数はないんだろうか。 $2$ 乗しても値が変わらない数は、他にないんだろうか」

ユーリ「むむ……その《先生トーク》からすると、 思いがけないところにそーゆー数があるんだね？」

僕「ねえ、ユーリ。そういう探りを入れるのはやめようよ」

ユーリ「へーい……でも、 $0$ と $1$ の他にはもうないと思うけど」

僕「ユーリはどうしてそう思ったんだろう」

ユーリ「だって、なさそーだもん。 あのね、マイナスの数って $2$ 乗したらプラスになっちゃうじゃん？　さっきの、 $$ (-3)^2 = 9 $$ みたいに。ってことは、 マイナスの数は《$2$ 乗しても変わらない数》にはならない」

僕「なるほど。それはそうだね」

ユーリ「プラスの数だってそーだよ。たとえば、 $2$ 乗したら、 $3$ は $9$ になるじゃん？ $$ 3^2 = 9 $$ 《$3$ は $9$ になる》ってことは、 $2$ 乗したら自分より大きくなっちゃうから《$2$ 乗しても変わらない数》にはならない……あ、 小さくなることもある。 $0.1$ とか。 $$ 0.1^2 = 0.01 $$ 《$0.1$ は $0.01$ になる》んだから、小さくなる。 例外は $0$ と $1$ だけでしょ。 $0$ を掛けたら何でも $0$ だから、 $0$ に $0$ 掛けても $0$ のままだし、 $1$ に $1$ 掛けても大きさ変わらないから $1$ のまま」

僕「うん、ユーリは数の大きさに注目したんだね。

• $x < 0$（$0$ より小さい場合）
• $x = 0$（$0$ に等しい場合）
• $0 < x < 1$（$0$ と $1$ の間の場合）
• $x = 1$（$1$ に等しい場合）
• $x > 1$（$1$ より大きい場合）

の $5$ 通りに《場合分け》したことになる」

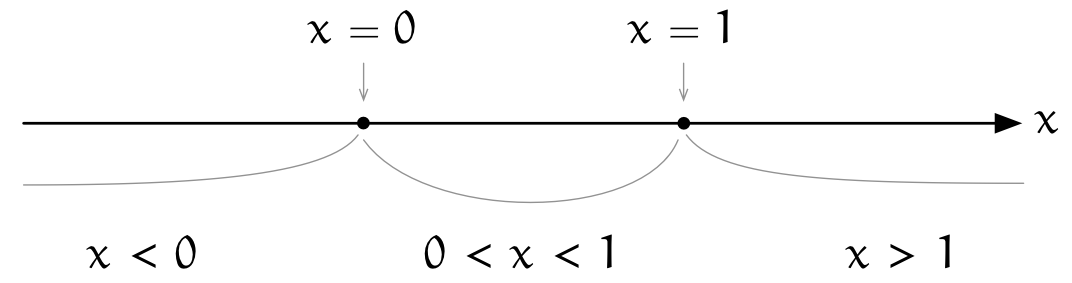
ユーリ「あー、そだね。そーなるね」

僕「こんな考え方もあるよ。 クイズの内容を方程式にしてしまうんだ」

ユーリ「ほーてーしき」

僕「《$2$ 乗しても変わらない数》というのは《言葉》で表しているけれど、 それを《数式》に置き換えて表してみよう。 $2$ 乗しても変わらないというのは、 その数を $x$ と置いたとき、 $x^2$ と $x$ とが等しいといえる。 だから、《$2$ 乗しても変わらない数》を $x$ と置くと、 $$ x^2 = x $$ という $x$ に関する方程式ができる」

ユーリ「ほほー。出たな数式マニア……ってほどじゃないか」

僕「ほどじゃないね。 これで《言葉》から《数式》に移されたことになる。 あとは方程式を解いていけばいい」

$$ \begin{array}{ccrcl} & \quad & x^2 &=& x \\ \Leftrightarrow & & x^2 - x &=& 0 \\ \Leftrightarrow & & x(x - 1) &=& 0 \\ \Leftrightarrow & & x = 0 &\,\REMTEXT{または}\,& x - 1 = 0 \\ \Leftrightarrow & & x = 0 &\,\REMTEXT{または}\,& x = 1 \\ \end{array} $$

ユーリ「……」

僕「これで、 $x^2 = x$ を満たす $x$ は $0$ と $1$ しかないことがわかった」

ユーリ「お兄ちゃん、いま式をサクサク書いたけど、この、 $$ \Leftrightarrow $$ はいったい何？」

僕「え？　話したことなかったっけ。 これは、 $$ P \Leftrightarrow Q $$ と書いたとき、左右の条件 $P$ と $Q$ とが《同値》であることを表す記号だよ。 数学の式変形で使うときには、 数式を《同値変形》していくときにこういう書き方をすることがある」

ユーリ「どーち？」

僕「うん、まずね、矢印は $\Rightarrow, \Leftarrow, \Leftrightarrow$ の三種類がある」

僕「この最後の場合、つまり $P \Leftrightarrow Q$ が成り立つとき、 条件 $P$ と条件 $Q$ は《同値》というんだ。 そして、 $P$ と $Q$ が数式で書かれているとき、 $P$ を表す数式を $Q$ を表す数式に変形させることを《同値変形》 と呼ぶことがある」

ユーリ「うーん……お兄ちゃん、それってあたりまえのことを難しく言ってる？」

僕「あたりまえってことはないと思うけど」

ユーリ「だってね、 $$ \begin{array}{ccrcl} &\qquad& x^2 &=& x \\ \Leftrightarrow & & x^2 - x &=& 0 \\ \end{array} $$ というのがあったとするじゃん？　これって $x$ を移項したってことでしょ？」

僕「そうだね、その通り」

ユーリ「それって、あたりまえじゃないの？」

僕「移項はあたりまえに見えるけれど、 さっきの問題を考えるときには、同値かどうかを意識するのは大事なんだよ。 もともとの疑問はこうだったよね。

ユーリ「そだね」

僕「いま言葉で表したことを $\Rightarrow$ を使って整理するね。 $$ \REMTEXT{(A)}\qquad \REMTEXT{《$x = 0$または$x = 1$》} \Rightarrow \REMTEXT{《$x$は$2$乗しても変わらない》} $$ この$\REMTEXT{(A)}$は成り立っていることはわかったけれど、 $$ \REMTEXT{(B)}\qquad \REMTEXT{《$x = 0$または$x = 1$》} \Leftarrow \REMTEXT{《$x$は$2$乗しても変わらない》} $$ この$\REMTEXT{(B)}$は成り立っているだろうか？」

ユーリ「ほほー。にゃるほど。$\REMTEXT{(A)}$と$\REMTEXT{(B)}$で、矢印の向きが《逆》になってる」

僕「そこだよ。まさにこれは《逆》というんだ。 $\REMTEXT{(A)}$の逆が$\REMTEXT{(B)}$で、 $\REMTEXT{(B)}$の逆が$\REMTEXT{(A)}$だね。 《$2$ 乗しても変わらない数が $0$ と $1$ 以外にあるだろうか》という問いは、 $\REMTEXT{(B)}$を確かめる問題になるわけだ。 そこで、数式の同値変形が大事になる」

ユーリ「なんで？」

僕「$\REMTEXT{(A)}$と$\REMTEXT{(B)}$の両方が成り立つなら、 $$ \REMTEXT{(C)}\qquad \REMTEXT{《$x = 0$または$x = 1$》} \Leftrightarrow \REMTEXT{《$x$は$2$乗しても変わらない》} $$ ということだからね。 《$x$ は $2$ 乗しても変わらない》ということを、 $x^2 = x$ という数式で表す。 そこから同値変形を続けていって、 《$x = 0$ または $x = 1$》にまでたどりつけるかどうか……それが大事になるからだよ」

ユーリ「同値変形って意識したことないよー」

僕「え？！　数式の《移項》や《展開》や《因数分解》なんかは、 ぜんぶ同値変形を作り出してるんだよ。 大事だから習ってるし、練習してる」

ユーリ「そっか。まーそれはいーとして、同値じゃない変形ってのもあるの？」

僕「もちろん、たとえば $x = y$ の両辺を $2$ 乗するような式変形。これは同値変形にならない」

$$ x = y \qquad \Rightarrow \qquad x^2 = y^2 $$

ユーリ「？」

僕「《$x = y$ が成り立つならば、 $x^2 = y^2$ が成り立つ》とはいえるよね。 でも、《逆》はいえない」

ユーリ「そゆことか。 $3^2 = (-3)^2$ はいえても、 $3 = -3$ とはいえないから？」

僕「そういうこと！」

グラフで考える

僕「ところで、グラフで考えると《$2$ 乗しても変わらない数》は $0$ と $1$ しかないことがよくわかるよ」

ユーリ「グラフで考える？」

僕「うん。ほら、 $y = x^2$ のグラフが放物線になるって話は知ってるよね。 こういうグラフ」

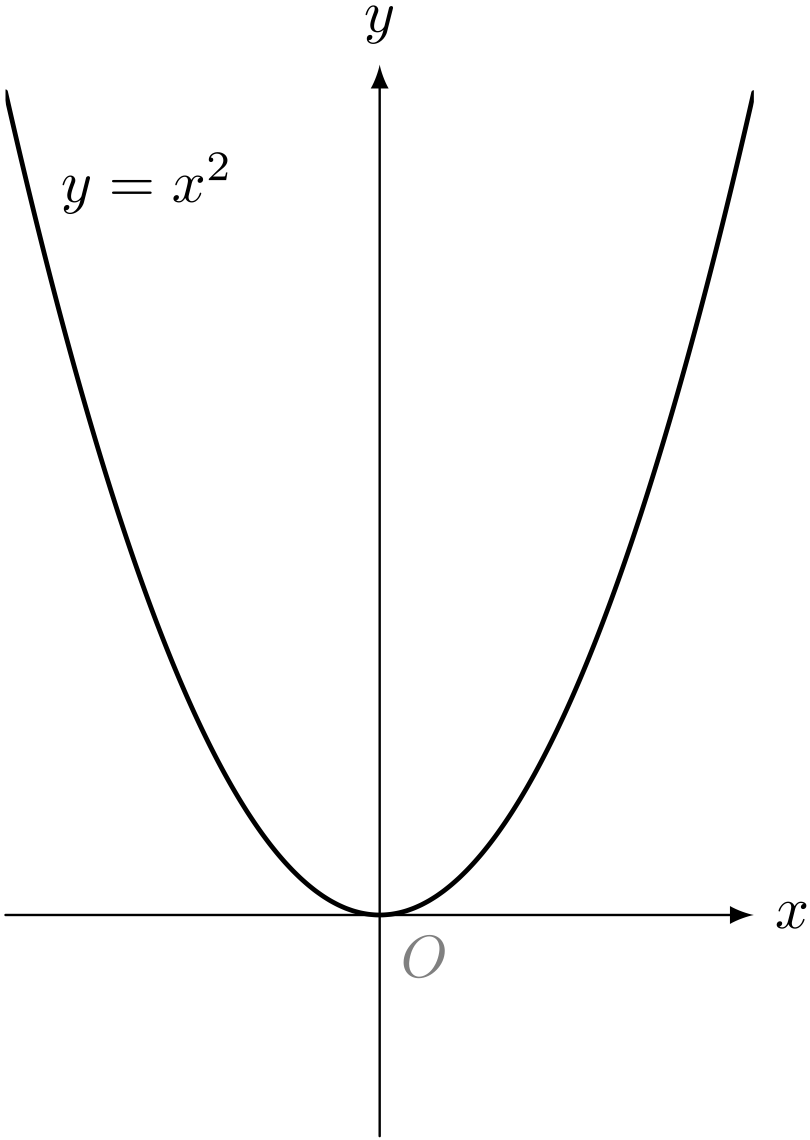
ユーリ「うん。わかる」

僕「この放物線の方程式は $y = x^2$ だから、 この放物線の上にある点は必ず $y = x^2$ という式を満たしていることになるよね」

ユーリ「えーと？　……うん。いーよ。 $(0,0)$ とか $(2,4)$ とか $(3,9)$ とか？」

僕「そうそう。そして、この放物線のグラフに重ねるようにして、 $y = x$ という直線のグラフを描いてみる」

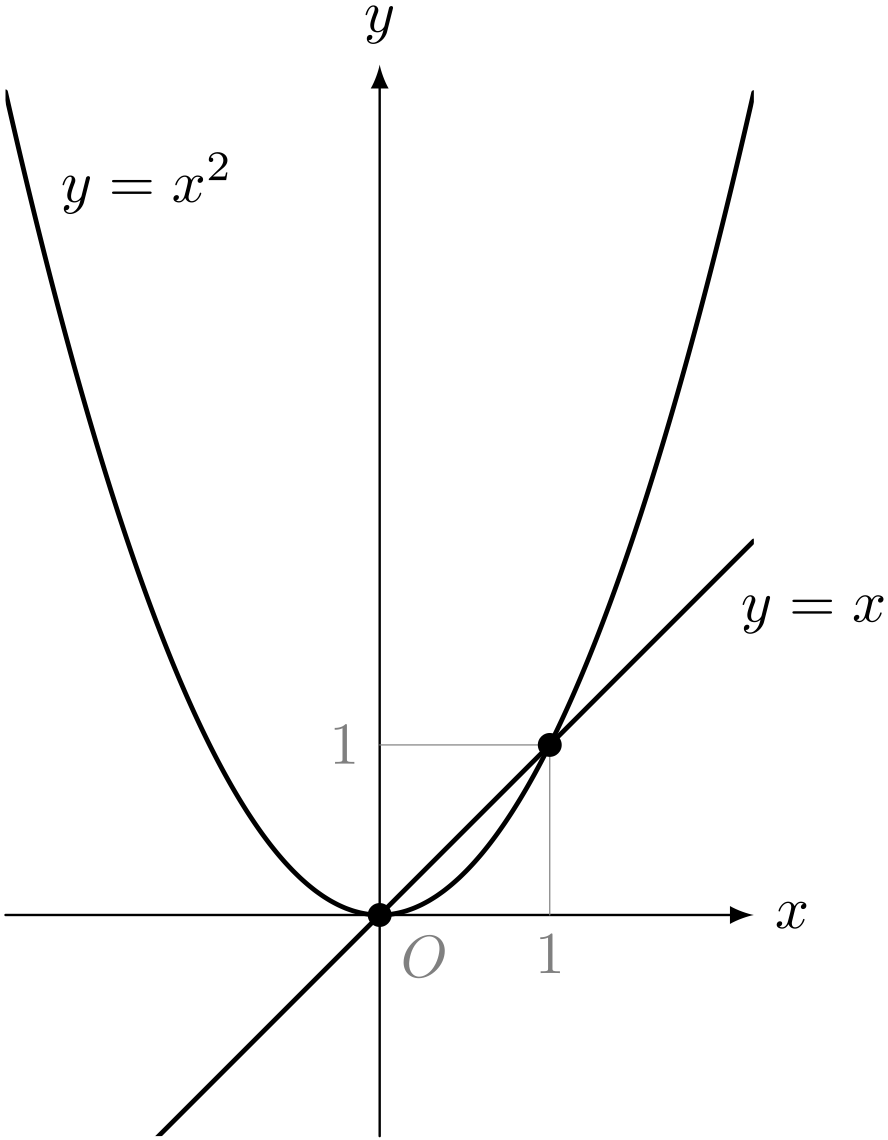
ユーリ「ふんふん？」

僕「この直線の方程式は $y = x$ だから、 この直線上の点は、 $y = x$ という式を満たしていることになる」

ユーリ「あ、わかってきた……」

僕「そこで、放物線 $y = x^2$ と、直線 $y = x$ の交点を考える。 すると、交点は、放物線と直線の《両方》の上にあるわけだから、 $y = x^2$ と $y = x$ の両方の式を満たす」

$$ \left\{\begin{array}{llll} y &= x^2 && \REMTEXT{放物線} \\ y &= x && \REMTEXT{直線} \\ \end{array}\right. $$

ユーリ「……連立方程式だ！」

僕「そうだね！　その通り。 だから、《放物線と直線の交点を求める》というのは、 《この連立方程式を解く》ということになる。 そしてグラフを見ると、交点は $2$ 個しかない。 $x = 0$ のときと、 $x = 1$ のときと」

ユーリ「にゃーるほど。だから、《$2$ 乗して変わらない数》ってゆーのは $0$ か $1$ といえる？」

僕「そうなるね。その二つしか交点がないから」

ユーリ「ふむふむ」

僕「それから、このグラフをよく見ると、 さっきの場合分けがどこに出てくるかもよくわかる」

ユーリ「さっきの場合分けって何だっけ」

僕「ユーリが考えたやつだよ。

• $x < 0$（$0$ より小さい場合）
• $x = 0$（$0$ に等しい場合）
• $0 < x < 1$（$0$ と $1$ の間の場合）
• $x = 1$（$1$ に等しい場合）
• $x > 1$（$1$ より大きい場合）

という $5$ 通りに分けたよね。それはこのグラフにきれいに現れている。放物線と直線が交わるところとそれ以外だね。 $2$ つの交点と、その交点で分けられた $3$ つの領域がある」

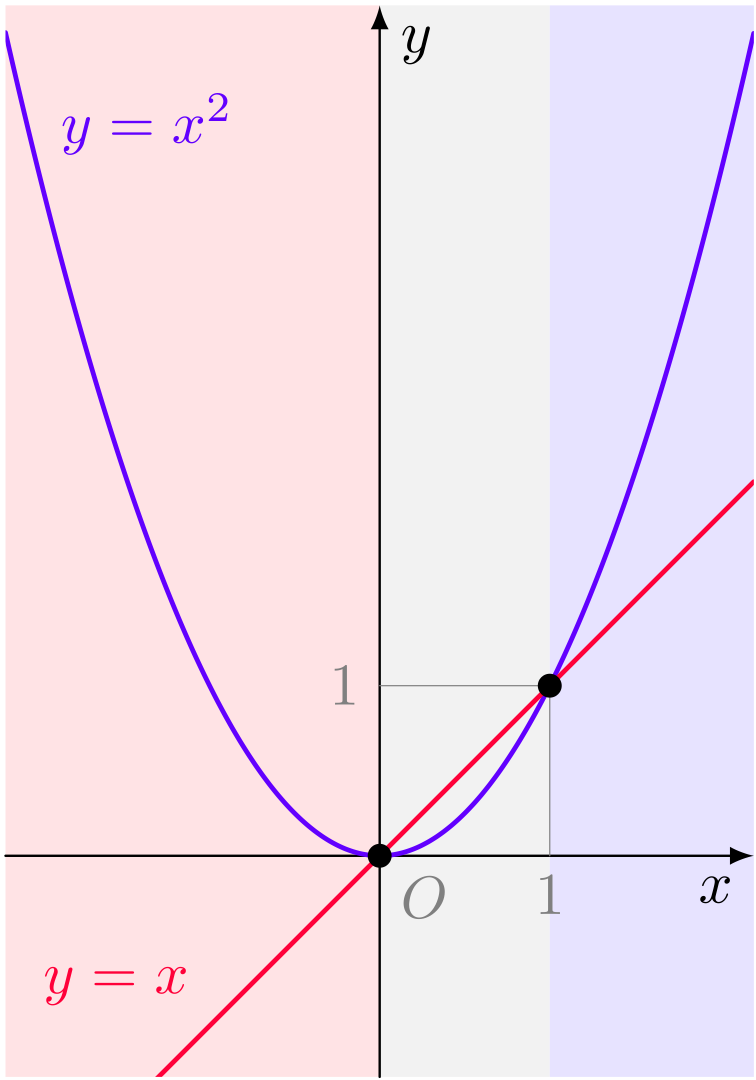
ユーリ「そっか！」

僕「放物線が直線より上の方になっているのは、 $x^2 > x$ になるところだよね。 そして、放物線が直線より下の方になっているのは $x^2 < x$ になるところ」

ユーリ「ははー、そだね。そして、交点のところはちょーど $x^2 = x$ になるところ！」

僕「そうそう、そういうこと。こんなふうに《グラフ》で表すと、 目で見て確かめることができる。なかなかいいよね」

ユーリ「……」

僕「数学だと、よくこういうことがあるよ。 《言葉》を使って表したり、 《数式》を使って表したり、 それからいまのように《グラフ》を使って表したり。 同じことでも、違った表し方をすると新しい発見があるんだね……って、これも《先生トーク》認定されそうかな。ははは」

ユーリ「……」

僕「ねえ、ユーリ？」

ユーリ「あのね？　他のグラフってない？」

僕「他のグラフ？」

ユーリ「いま、ほら、 $x$ と $y$ のグラフを描いたじゃん？　 $x$ と $x$ のグラフみたいなのってない？」

僕「$x$ と $x$ のグラフ……ごめん、何のことだかわからないなあ」

ユーリ「えー、ほら、お兄ちゃんが描いて教えてくれたじゃん。《マイナス×マイナス》のとき」

僕「よく覚えてないけど、描いてみてよ」

マイナス×マイナス

ユーリ「たとえば $3$ に $-1$ を掛けるとするじゃん？ $$ 3 \times (-1) $$ そーすると、 $3$ のところにあった点が、パタンと回って $-3$ に来るでしょ？」

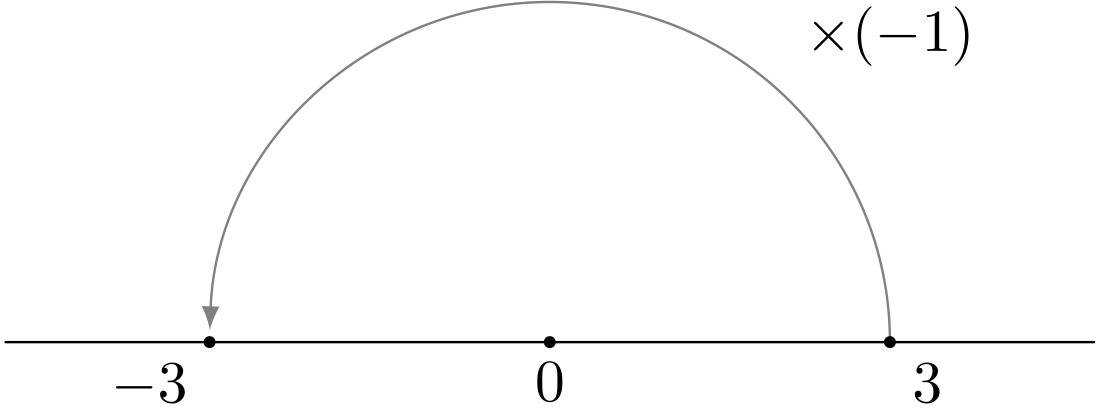
僕「そうなるね。 $-1$ を掛けたら」

ユーリ「だから《$-1$ を掛ける》ってゆーのは《パタンと回す》ことと同じ……って教えてくれたじゃん。 このグラフで」

僕「ああ、そういうことか。これはグラフとはいわなくて、数直線だよ」

ユーリ「何でもいーけどさ。そんで、これを使えば、マイナス×マイナスがプラスになるのは、 すごく納得いく。 だって、《$-3$ に $-1$ を掛ける》ってゆーのが《$-3$ の点をパタンと回す》ことなら、 確かに $3$ になるから！」

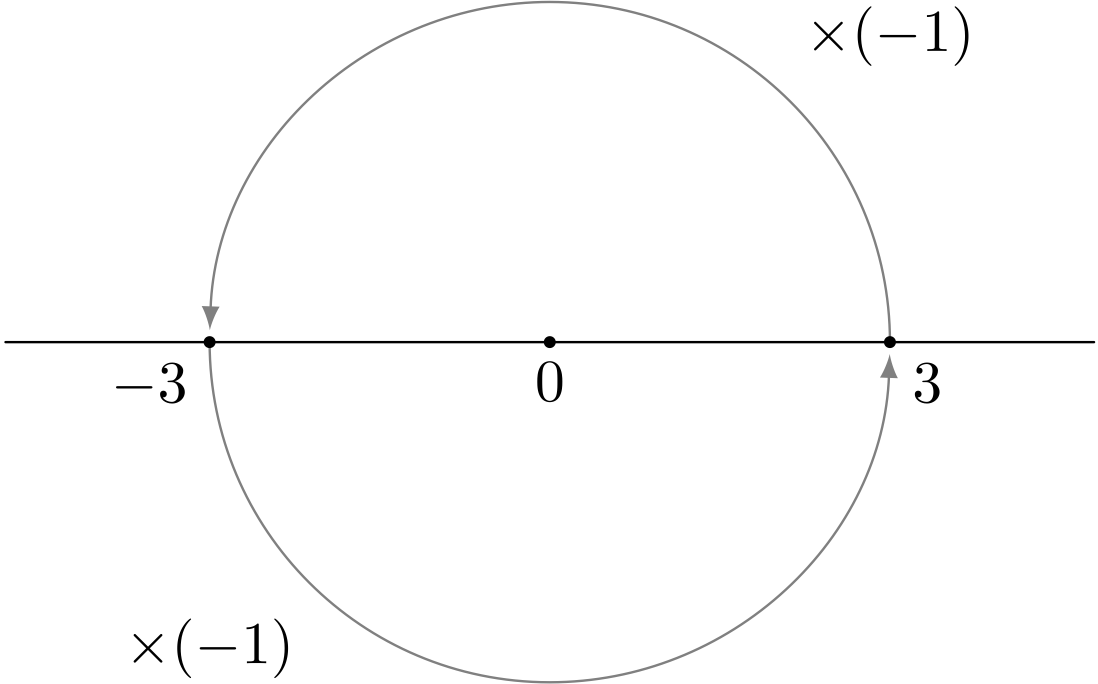
僕「そうだね。とても納得いくよね……これのことを思い出してたの？」

ユーリ「そだよん。 いまのは、 $3$ に $-1$ を掛けてパタンパタン動かしたけど、 もしも、 $2$ 乗したら、どんな動きになるかにゃあ……って、考えてたの」

僕「なるほど！　ユーリ、おもしろいこと考えたなあ！」

ユーリ「さっきから考えてたんだけど、これってそんなに難しくないよね？」

僕「そうだね」

ユーリ「$0$ と $1$ は、すぐにわかるの。 だって、この点は $2$ 乗してもまったく動かないわけでしょ？」

僕「うんうん、そうなる。不動点だ。そして数直線上で不動点なのはその $2$ つだけだね！」

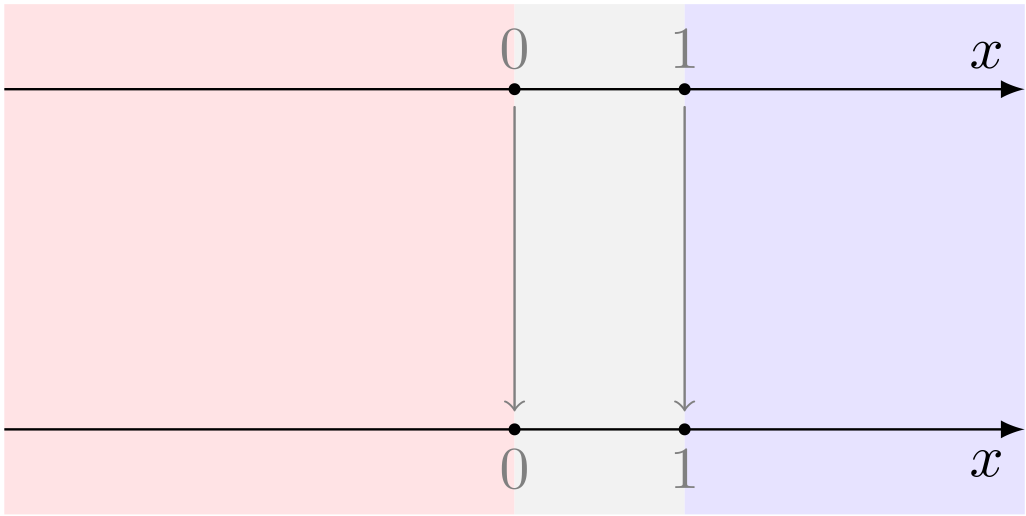
ユーリ「それから、 $x > 1$ にある点は、 $2$ 乗するとすんごく遠くに行くの。右のほうに。 右にある点ほど、ずっと右に行くんだよ。だって $2$ 乗だから」

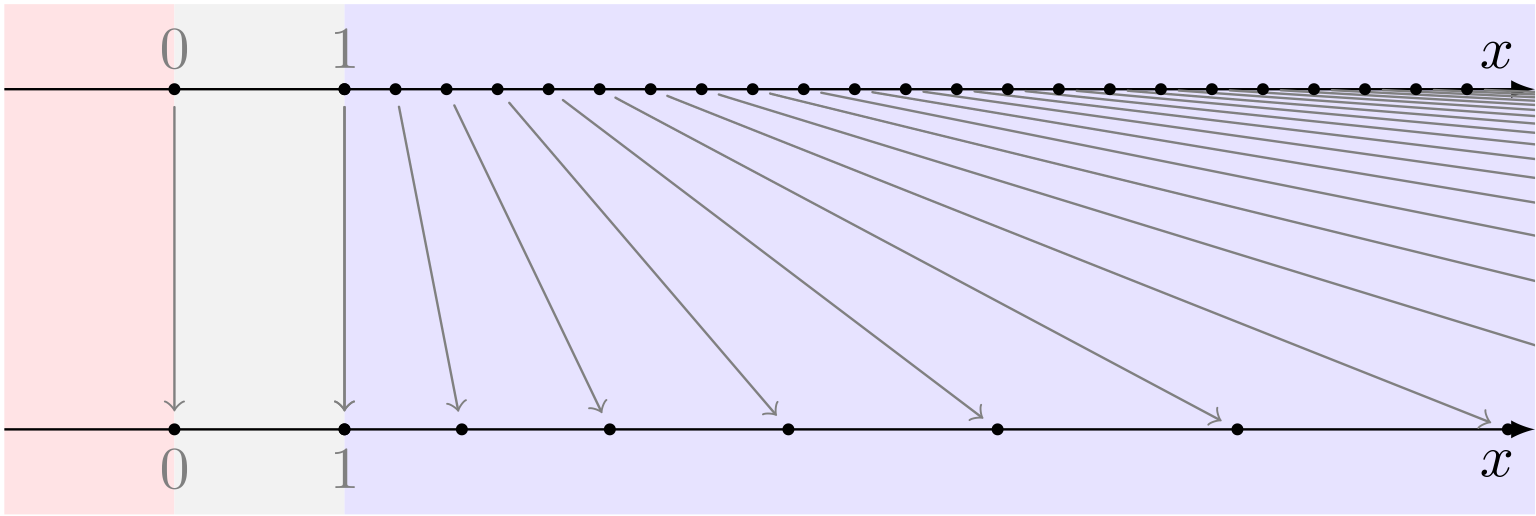
僕「そうなるね。 $2$ は $4$ に、 $3$ は $9$ に、 $4$ は $16$ に……そして、 $10$ は $100$ に」

ユーリ「$0 < x < 1$ の点がちょっと言いにくいんだけど、 $0$ の方にぎゅっと押しつけられる感じ？　しかも、左にある点ほど、ずっと $0$ に近づくの」

僕「確かに。 $\frac12$ は $\frac14$ に、 $\frac13$ は $\frac19$ に……」

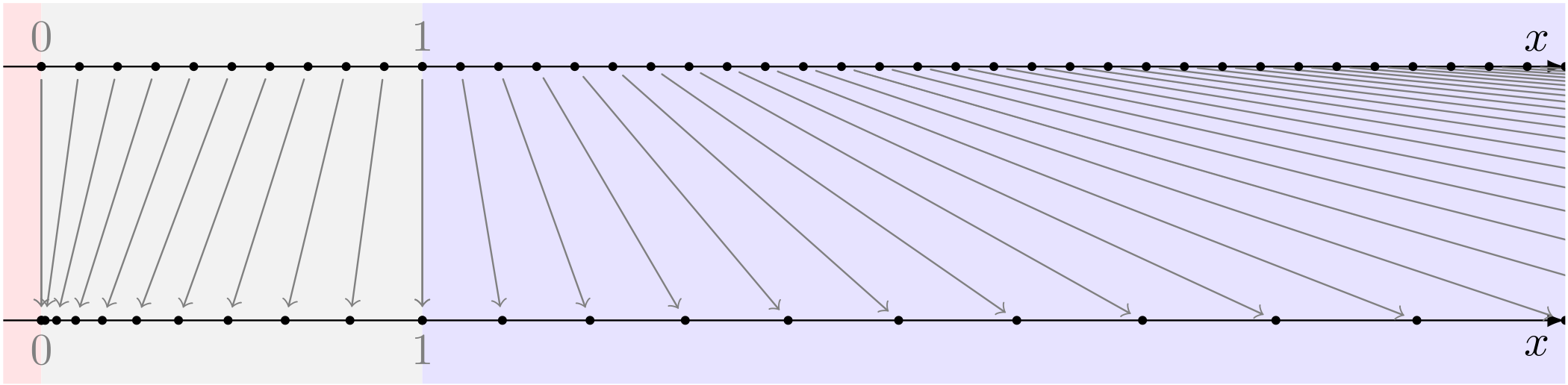
ユーリ「そんで、残りはマイナスだけど、これはカンタン。 だって、パタンと回した後で、さっきと同じことすればいーから」

僕「そうなるね。ということは、 $x < -1$ の点は、ずっと右に行き、 $x = -1$ の点は $x = 1$ に重なり、 $-1 < x < 0$ の点は $0$ に近いものほど、もっと $0$ に近づく」

グラフと数直線

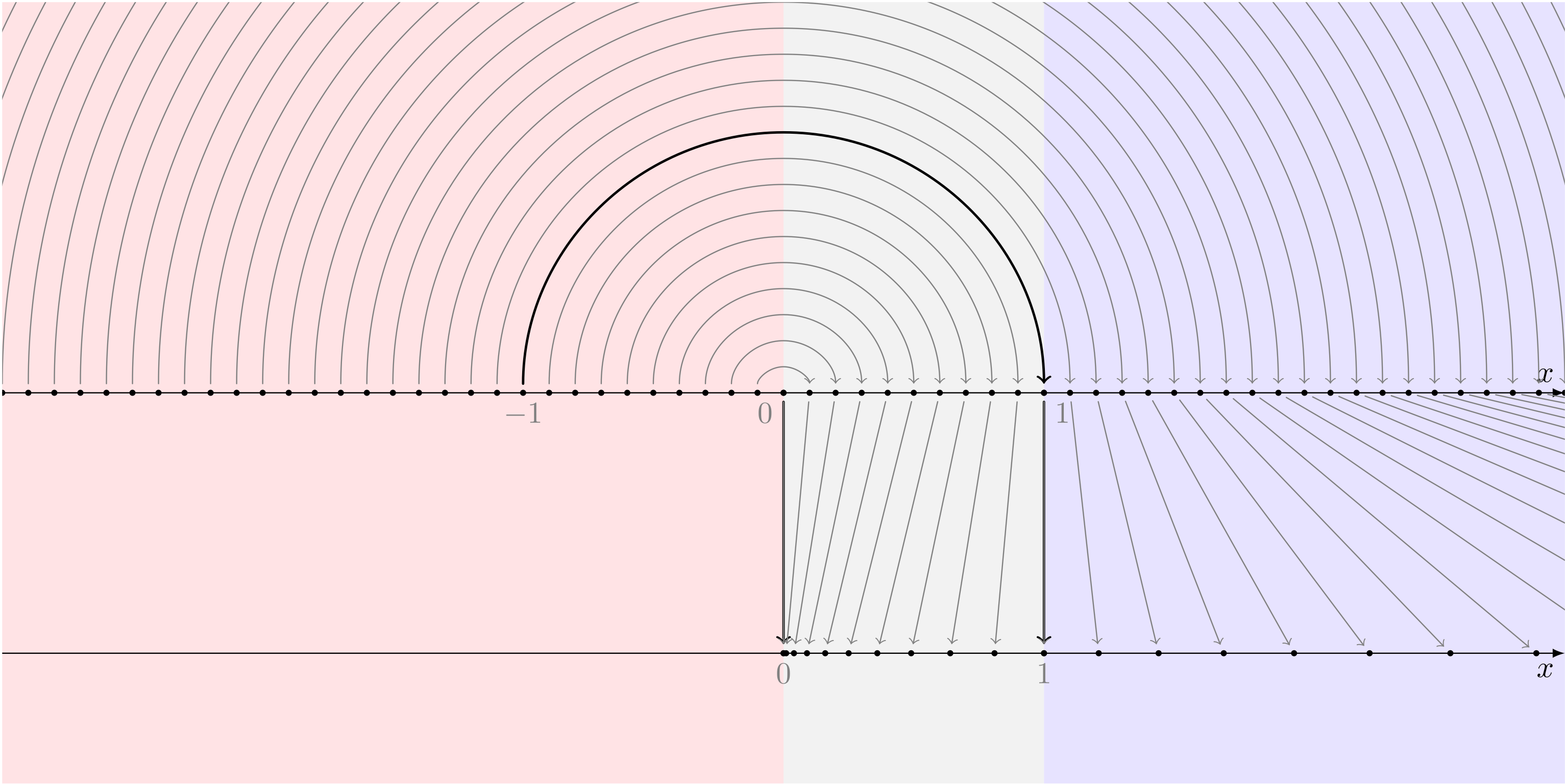
僕「……ユーリのおもしろい話で、お兄ちゃんも気付いたよ。 さっきの放物線のグラフとの関係」

ユーリ「何のこと？」

僕「いまユーリは数直線上の $x$ を $x^2$ に移すっていう問題を考えたよね。 $0$ と $1$ だけ不動点で、あとはいろいろ動いた」

ユーリ「そだね。いろいろね」

僕「その《動き》は、さっきの放物線のグラフから読み取れるんだよ。 まあ、あたりまえのことだけど」

ユーリ「何言ってるかわかんない」

僕「たとえば $a$ が $a^2$ に動くのはこんな感じになるよ。

• $x$ 軸の点 $a$ に垂直線を引いて、放物線 $y = x^2$ との交点を求める。
• 交点から水平線を引いて、直線 $y = x$ との交点を求める。
• その交点から垂直線を引いて $x$ 軸との交点を求めると、そこが $a^2$ になる。

だから、グラフで $a$ から $a^2$ への動きがわかるんだね」

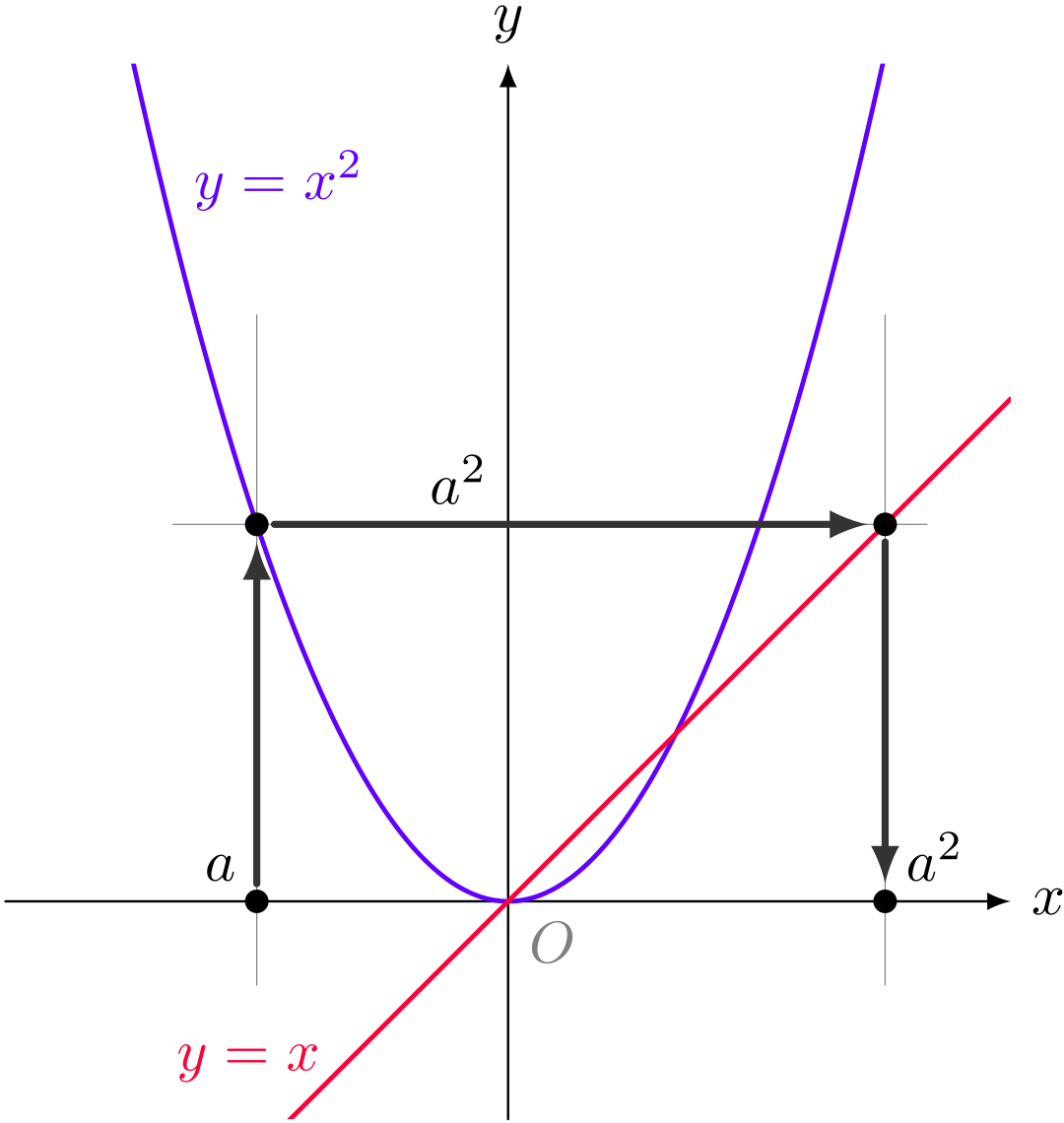
ユーリ「うーん、それは何で？」

僕「垂直線と放物線との交点を求めるところで、 $a$ から $a^2$ はもう求められたんだけど、 できた $a^2$ の値は $y$ 座標として表されている。 その $y$ 座標を $x$ 座標に移すために直線 $y = x$ を使ったんだよ」

ユーリ「なーるほど。放物線にぶつかって、直線にぶつかって、戻ってくるんだ」

僕「$x < 0$ の数いくつかで試してみよう」

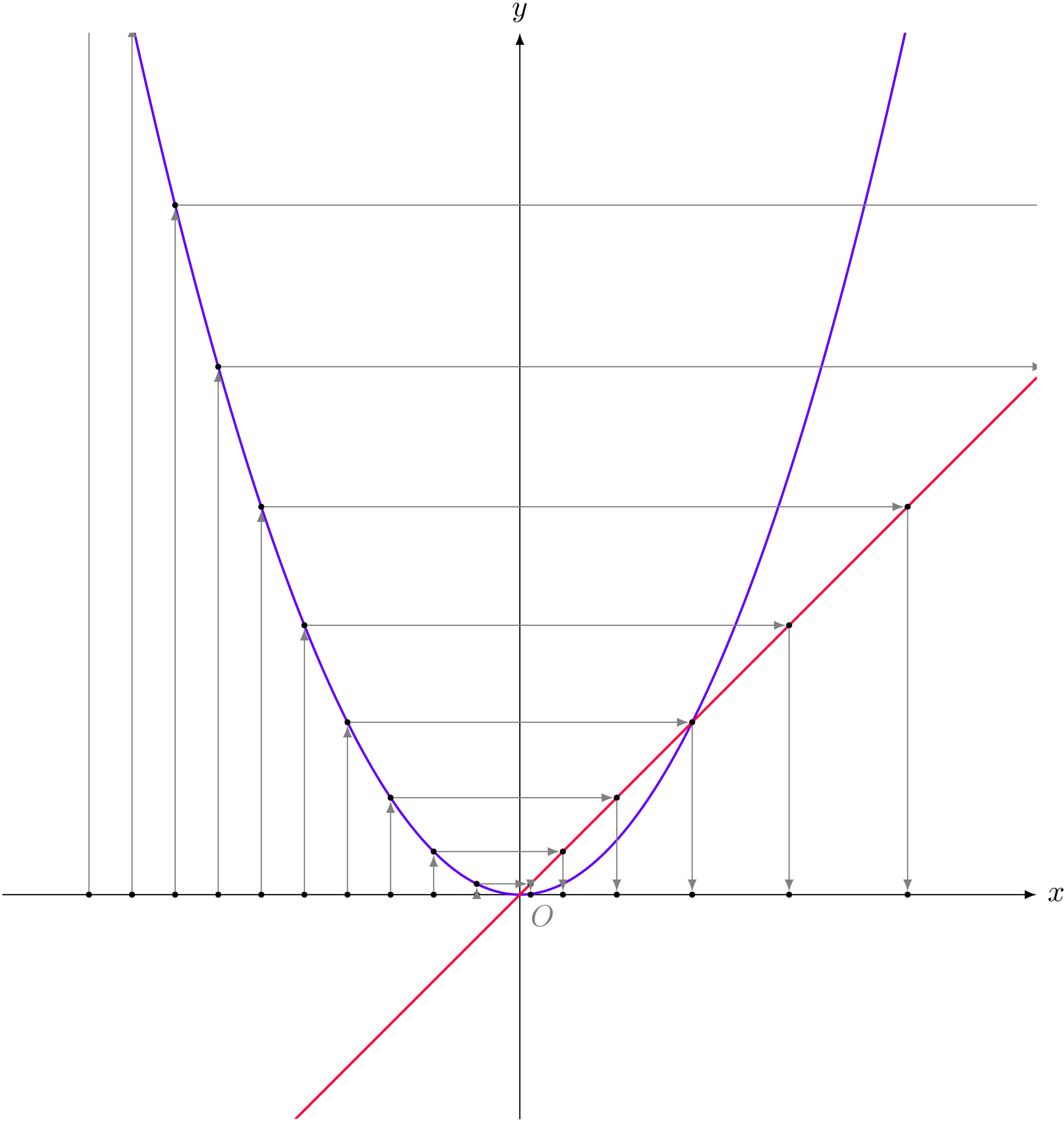
ユーリ「確かにー！」

僕「この図を使うと、もっとわかることがあるよ。 $x$ 座標が $a$ になっている点は、 $2$ 乗すると $a^2$ に動く。 だったら、 $2$ 乗すると $b$ に動いてくる点は、もともとどこにあったか？」

ユーリ「……ははーん。反対にたどるんでしょ！」

僕「そうだね。ただし、もともとの点は一つとは限らない。 反対にたどると、放物線と $2$ 点で交わるときがあるからね」

ユーリ「そーだね！」

僕「反対にたどってみよう」

• $x$ 軸の点 $b$ に垂直線を引いて、直線 $y = x$ との交点を求める。 $b \geq 0$ とするよ。
• 交点から水平線を引いて、放物線 $y = x^2$ との交点を求める。
• ここで $2$ つに分かれるときがある！
• 交点から垂直線を引いて $x$ 軸との交点を求めると、そこは $-\sqrt{b}$ と $\sqrt{b}$ になる。

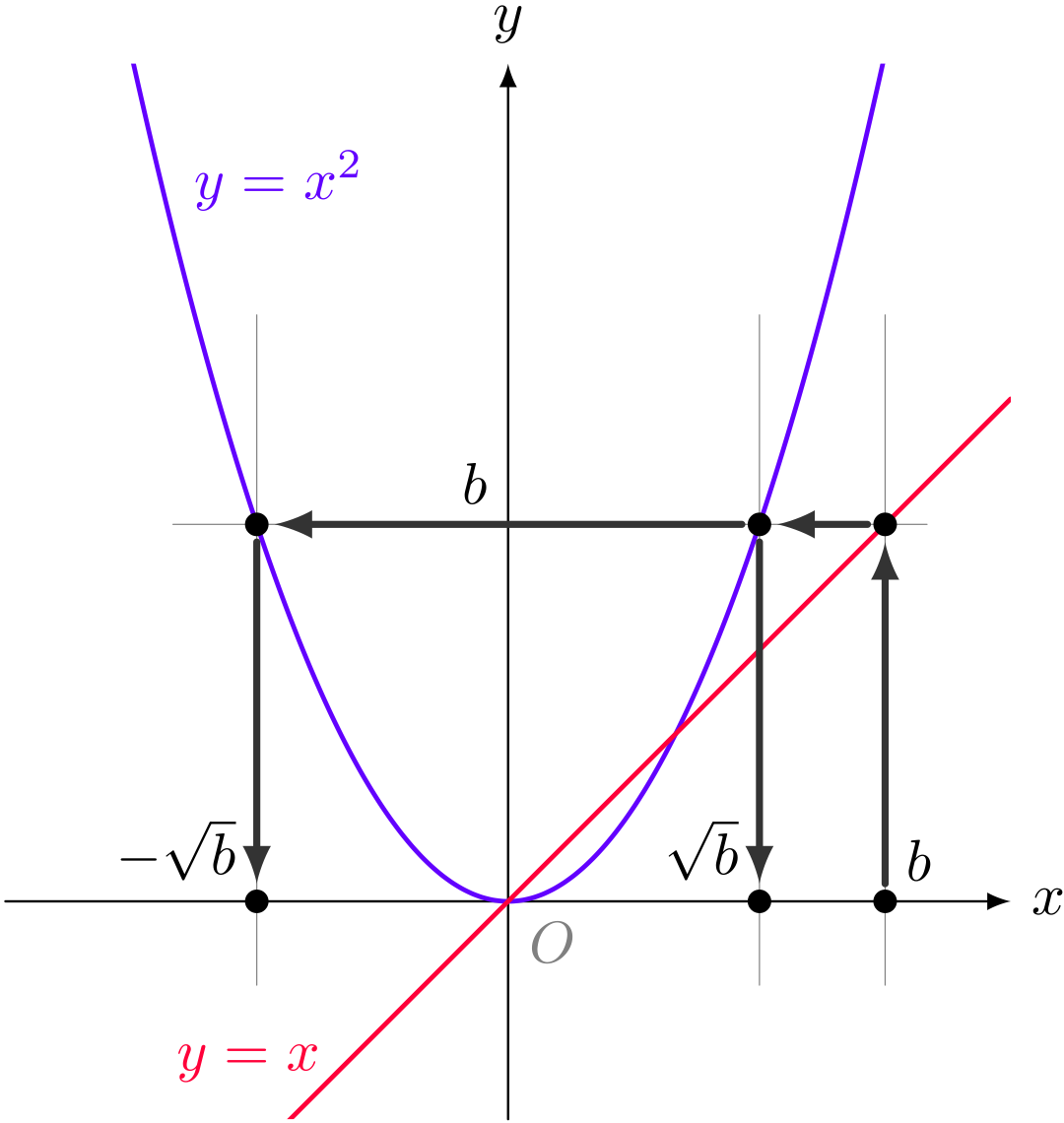
ユーリ「$9$ から始めたら、 $-3$ と $3$ に戻ってくる？」

僕「そういうことになる。 $-\sqrt{9} = -3$ で $\sqrt{9} = 3$ だからね。ちゃんと $2$ つの答えが出てくる。 数を $2$ 乗するときに起きることが、 こんなふうにグラフに現れてくるのは楽しいね！」