![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/数を作ろう』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
ミルカさん:数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
瑞谷先生:司書の先生。定時になると下校時間を宣言する。
いまは放課後。ここは高校の図書室。 僕とテトラちゃんは、ミルカさんと《有理数の完備化》について話し合っていた(第159回参照)。
ミルカ「そう。……ところで、ここまで考えてきたコーシー列による完備化を別の角度から眺めよう。まずは……」
テトラ「ちょ、ちょっとお待ちください。いったんここまでのお話を整理させてください」
ミルカ「ふむ」
テトラ「ミルカさんは、《有理数全体の集合》から《実数全体の集合》を構成するというお話をしてくださっていました」
僕「コーシー列による完備化だね」
テトラ「はい……そして、そのお話はこんなふうに進みました」
僕「そうだね。その流れの通りだと思うよ」
テトラ「差の数列を考えるところがおもしろいと思いました。 同じ数に収束する数列を見つけるのに、差が $0$ になる数列同士を仲間にするところです。同一視、ですね」
僕「そうだね。これで《コーシー列による完備化》ができた」
テトラ「完備化……どうしてこれを完備化というのでしょうか」
ミルカ「収束先の数までが、その集合の中に備わっているから。 有理数では、コーシー列を使って有理数の《外》へ抜け出すことができてしまう。 しかし、完備化によって実数全体の集合を作ると、 コーシー列を使ってその集合の《外》へ抜け出すことはできない。 収束に関して閉じていることになる。正確には有理数のコーシー列の収束とは別に、 実数のコーシー列についての収束を検討する必要があるけれど」
テトラ「先ほども、そういうお話がありましたね(第159回参照)。 抜け出せるかどうか」
ミルカ「さて、私がこれから考えたいのは、別の完備化だ」
僕「別の完備化?」
テトラ「完備化に何種類もあるんですか?」
ミルカ「そういう意味ではない。先ほどのテトラの《まとめ》に出てきた《重要な概念》を少し変えるのだ」
僕「《重要な概念》というのは、《コーシー列》のこと?」
ミルカ「《コーシー列》を定義するために必要になる《重要な概念》のこと。 その《重要な概念》はまた、 《数列同士の差》を考えるときにも必要だ。 つまり、完備化を行うときには本質的な役割を果たすことになる。 さて、その《重要な概念》は何かな?」
ミルカさんはそう言って、いたずらっぽく微笑んだ。

テトラ「《コーシー列》というと、 $\XABS{a_m - a_n}$ が $0$ に収束する数列ですよね。 《数列同士の差》というのは、 $\XABS{a_n - b_n}$ です」
僕「ミルカさん、もしかして、絶対値? 絶対値が《重要な概念》になるの?」
ミルカ「その通り。これから私たちは別の《絶対値》を考える。それを《$2$ 進絶対値》と呼ぶことにする」
テトラ「$2$ 進絶対値……」
ミルカ「これから考えるのは、有理数の $2$ 進絶対値だ。 ふだん私たちが使っている絶対値が《$0$ からの距離》を表現しているように、 $2$ 進絶対値も数の《$0$ からの距離》を表現していると見なすことができる」
テトラ「す、すみません。さっぱりわからないんですが……」
ミルカ「まだ何も説明していないのだから、わからないのは当然だ。わかったら驚きだよ、テトラ」
テトラ「は、はい」
ミルカ「まずは定義から。有理数の $2$ 進絶対値は以下のように定義される」
《有理数の $2$ 進絶対値》
$0$ 以外の有理数 $x$ を、
$$
x = 2^n \cdot \dfrac{b}{a}
$$
と表現する。ここで、 $n$ は整数、 $a,b$ は奇数である。
このとき、 $0$ 以外の有理数 $x$ の $2$ 進絶対値 $\XABS{x}_2$ を、
$$
\XABS{x}_2 = \dfrac{1}{2^n}
$$
と定義する。
また、 $0$ の $2$ 進絶対値 $\XABS{0}_2$ を、
$$
\XABS{0}_2 = 0
$$
と定義する。
テトラ「……」
僕「……」
ミルカ「さて?」
テトラ「……すみません。やっぱりわかりません」
僕「違うよ。テトラちゃん。ここは考えどころだ。僕もさっぱり意味がわかってないけれど、 ミルカさんから《定義が与えられた》んだから、僕たちがやることは決まっている」
テトラ「え……」
僕「もちろんそれは、《例を作る》ことだよ!」
テトラ「あ。そ、そうでした。《例示は理解の試金石》ですものね。 例を作ろうともしないで、わからないなんて言っちゃだめですね……」
ミルカ「たとえば、クイズ。 $\XABS{6}_2$ を求めよ」
クイズ
有理数 $6$ の $2$ 進絶対値、
$$
\XABS{6}_2
$$
を求めよ。

僕「まずは、定義から、 $$ 6 = 2^n \cdot \dfrac{b}{a} $$ を満たす整数 $n$ と奇数 $a,b$ を見つけないと」
テトラ「あ、分数ですから $a$ は非 $0$ ですよね。ゼロ割になりますから」
僕「テトラちゃん、 $a$ は奇数だからもともと $0$ は除外されているよ……」
テトラ「そうでした……」
僕「$6$ は $2\times3$ だから、こうかな? $$ 6 = 2^1 \cdot \dfrac{3}{1} $$ つまり、 $n = 1, a = 1, b = 3$ だね」
テトラ「ということは、 $n$ が $1$ ですから、 $2$ 進絶対値は、 $$ \XABS{6}_2 = \dfrac{1}{2^1} = \dfrac{1}{2} = 0.5 $$ でしょうか」
ミルカ「それでいい。 $0.5$ でもいいし、 $\dfrac{1}{2}$ のままでもいい。とにかく、 $\XABS{6}_2$ がわかった」
クイズの答え
$$
\XABS{6}_2 = \dfrac12
$$
テトラ「あ、あれ……たった一個の例を考えただけなのに《難しくないかも》と思えてきました。 不思議です!」
僕「そうだね。僕もそう思うよ。この調子でいくつか例を作ってみようよ。 たとえば、 $\XABS{20}_2$ とか」
テトラ「$20$ は、 $2^2 \times 5$ ですね。ということは、 $$ 20 = 2^2 \cdot \dfrac{5}{1} $$ になって、 $n = 2$ です。ですから、 $$ \XABS{20}_2 = \dfrac{1}{2^2} = \dfrac{1}{4} $$ になります! ちょっとコツがわかってきました」
僕「そうだね。これって、 $2$ 進絶対値を考えるときには $2^n$ だけが効くんだ。 $a,b$ は関係がない。 言い換えると、 $2$ 進絶対値というのは《$2$ で何回割ることができるか》を表しているのかも。 $2$ で割ることができる回数が多いほど、 $2$ 進絶対値は $0$ に近づくね」
テトラ「そうですね! だって、 $2^n\cdot\dfrac{b}{a}$ から $\dfrac{1}{2^n}$ を求めるわけですから」
$$ \XABS{2^n\cdot\dfrac{b}{a}}_2 = \dfrac{1}{2^n} $$ミルカ「では、 $2$ で割り切れない $9$ の $2$ 進絶対値はどうだろう」
僕「なるほど、 $9$ は奇数だから……簡単だよ。 $2^0 = 1$ を使えばいい。こうだね。 $$ 9 = 2^0 \cdot \dfrac{9}{1} $$ だから、 $2^0$ の逆数が求める $2$ 進絶対値で、 $$ \XABS{9}_2 = \dfrac{1}{2^0} = \dfrac{1}{1} = 1 $$ になる」
テトラ「あれ、ということは、奇数の $2$ 進絶対値はいつでも $1$ ですか?」
僕「そうなるね。負でもそうだね」
$$ \XABS{\pm 1}_2 = \XABS{\pm 3}_2 = \XABS{\pm 5}_2 = \cdots = 1 $$テトラ「$2$ 進絶対値は等しくなることもあるんですね」
ミルカ「ふつうの絶対値でもそうだ。 $\XABS{1} = \XABS{-1} = 1$」
テトラ「あ、確かに」
ミルカ「奇数の $2$ 進絶対値が必ず $1$ になるのはわかった。 それでは、偶数の $2$ 進絶対値はどうだろう」
僕「それは、 $2$ で何回割れるかによるよ。 $2, 6, 10, 14$のように、$2 \times \REMTEXT{奇数}$だったら、$2$進絶対値は$\dfrac12$だね」
$$ \begin{align*} \XABS{2}_2 & = \XABS{2\cdot\frac11}_2 = \frac12 \\ \XABS{6}_2 & = \XABS{2\cdot\frac31}_2 = \frac12 \\ \XABS{10}_2 & = \XABS{2\cdot\frac51}_2 = \frac12 \\ \XABS{14}_2 & = \XABS{2\cdot\frac71}_2 = \frac12 \\ &\vdots \\ \end{align*} $$テトラ「ははあ、いまのは、 $1,3,5,7\ldots$ に $2$ を掛けたものですね。 だったら、 $1,3,5,7,\ldots$ に $2^2$ を掛けたものの $2$ 進絶対値は $\dfrac1{2^2}$ になるんですね」
$$ \begin{align*} \XABS{4}_2 & = \XABS{2^2\cdot\frac11}_2 = \frac1{2^2} \\ \XABS{12}_2 & = \XABS{2^2\cdot\frac31}_2 = \frac1{2^2} \\ \XABS{20}_2 & = \XABS{2^2\cdot\frac51}_2 = \frac1{2^2} \\ \XABS{28}_2 & = \XABS{2^2\cdot\frac71}_2 = \frac1{2^2} \\ &\vdots \\ \end{align*} $$僕「そうだね。いくらでも繰り返せる。奇数に $2^3$ を掛ける、奇数に $2^4$ を掛ける……とね」
$$ \begin{align*} \XABS{8}_2 & = \XABS{2^3\cdot\frac11}_2 = \frac1{2^3} \\ \XABS{24}_2 & = \XABS{2^3\cdot\frac31}_2 = \frac1{2^3} \\ \XABS{40}_2 & = \XABS{2^3\cdot\frac51}_2 = \frac1{2^3} \\ \XABS{56}_2 & = \XABS{2^3\cdot\frac71}_2 = \frac1{2^3} \\ &\vdots \\ \end{align*} $$ $$ \begin{align*} \XABS{16}_2 & = \XABS{2^4\cdot\frac11}_2 = \frac1{2^4} \\ \XABS{48}_2 & = \XABS{2^4\cdot\frac31}_2 = \frac1{2^4} \\ \XABS{80}_2 & = \XABS{2^4\cdot\frac51}_2 = \frac1{2^4} \\ \XABS{112}_2 & = \XABS{2^4\cdot\frac71}_2 = \frac1{2^4} \\ &\vdots \\ \end{align*} $$テトラ「あたし、 $2$ 進絶対値さんと《お友達》になれそうです!」
ミルカ「そう? それなら、このクイズは?」
クイズ
$$
\XABS{0.2}_2
$$
を求めよ。
テトラ「$0.2$ の $2$ 進絶対値?」
ミルカ「$0.2$ も有理数だから」

僕「……」
テトラ「$0.2$ は、 $0.1$ と $2$ を掛けますよね……あれ?」
僕「これは《定義にかえれ》だね」
テトラ「定義にかえれ……ああ、わかりました。分数に直せばいいんですね! $$ 0.2 = \dfrac{2}{10} = \dfrac{1}{5} $$ ですから、 $$ 0.2 = 2^0 \cdot \dfrac{1}{5} $$ になります。 ということは、 $2^0$ の逆数で、 $$ \XABS{0.2}_2 = \dfrac{1}{2^0} = 1 $$ になります」
僕「へえ、 $0.2$ は $2$ 進絶対値としては、奇数と同じなんだね」
ミルカ「$0$ と $0.2$ の《$2$ 進距離》は、 $0$ と奇数との《$2$ 進距離》に等しいといえる」
僕「$2$ 進距離?」
ミルカ「有理数 $x$ の $2$ 進絶対値 $\XABS{x}_2$ が定義できたのだから、 二つの有理数 $x,y$ に対して、 $$ \XABS{x - y}_2 $$ を《$2$ 進距離》と呼ぶのは自然なことだと思うが」
テトラ「な、なるほど……」
僕「なるほどね」
ミルカ「テトラと君がたくさんの有理数 $x$ について、 $2$ 進絶対値 $\XABS{x}_2$ を計算してくれた。 それはすなわち、 $0$ と $x$ の $2$ 進距離を計算したことになる」
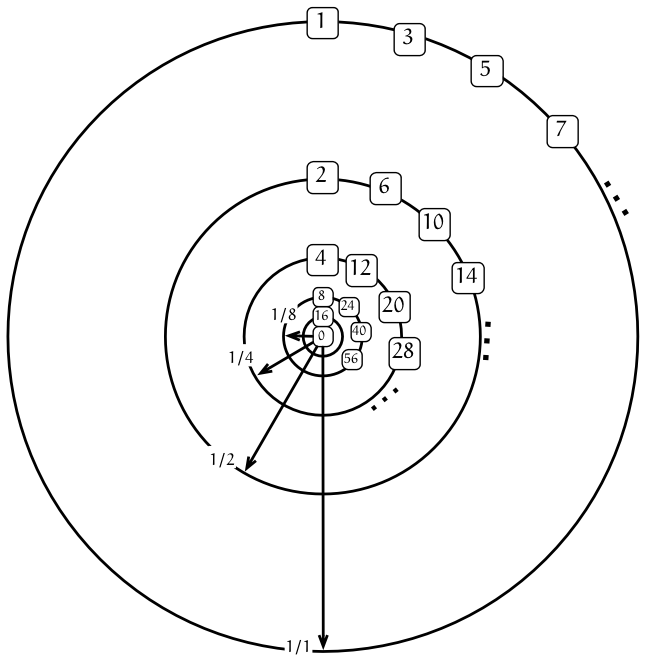
テトラ「せ、先輩方! あたし、ひらめきました。それって、図に描けます! $0$ より遠い人もいますし、 $0$ に近い人もいます。人じゃなくて有理数ですけど。同心円の上にいるんですよ!」
ミルカ「同心円?」
$0$ と $x$ との $2$ 進距離の様子
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年6月10日)
この記事は『数学ガールの秘密ノート/数を作ろう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!