第146回 シーズン15 エピソード6

波を見る（後編）

リビングにて

僕「これで、 $$ y = \sin x + \sin 2x $$ のグラフが描けるよ。オプションを付けて、 $y = \sin x$ を赤で、 $y = \sin 2x$ を青で表示しようか」

ユーリ「……ねえ、お兄ちゃん？」

僕「……なに？」

ユーリ「じーっとグラフ見て、何考えてんの？」

僕「ユーリこそ、グラフを見て、何を考えている？」

ユーリ「あのね、あまりこんなにじーっと見たことなかったなーって。 サインカーブは知ってたけど、重ねるとこんな形になるんだーって」

僕「そうだね。 $\sin x$ と $\sin 2x$ を足し合わせる。 すると重ね合わせた波はこんな形になるんだね」

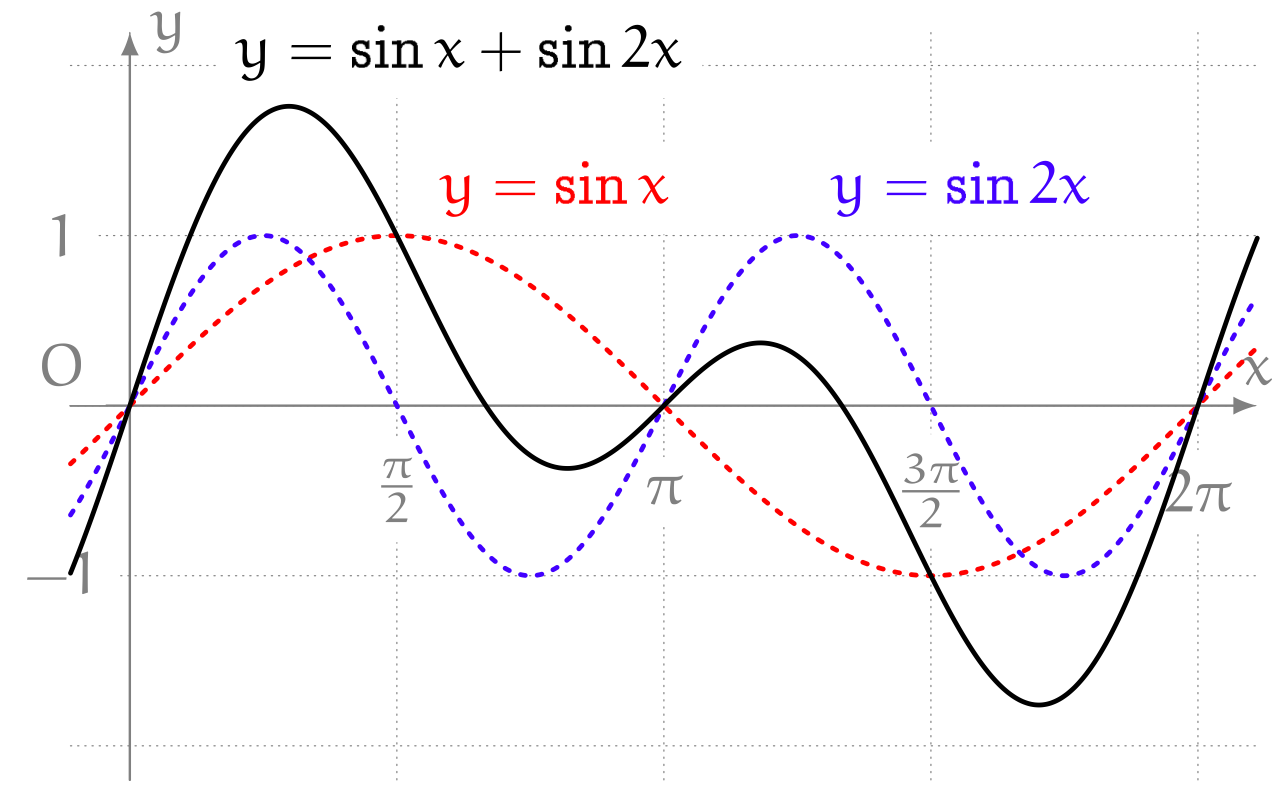
ユーリ「$0$ と $\pi$ と $2\pi$ のところが、ちょうど $0$ になってる」

僕「ああ、そうだね。 $x = 0, \pi, 2\pi$ を $y = \sin x + \sin 2x$ に代入すると、 $y = 0$ になるねえ」

ユーリ「この赤い線の $y = \sin x$ と、青い線の $y = \sin 2x$ の両方がちょーど、 うまい具合に、ぴったり $0$ になるからだよね。 $0 + 0$ は $0$ だもん」

僕「その通りだね。 たとえば $x = \pi$ のとき $\sin x = \sin \pi = 0$ だし、 $\sin 2x = \sin 2\pi = 0$ になる。 それがちょうど重なるから、重ねたものもちょうど $0$ になる。でも、よく見てごらんよ。 $y = 0$ になるのはそこだけじゃない。ここと、ここも $y = 0$ になってる」

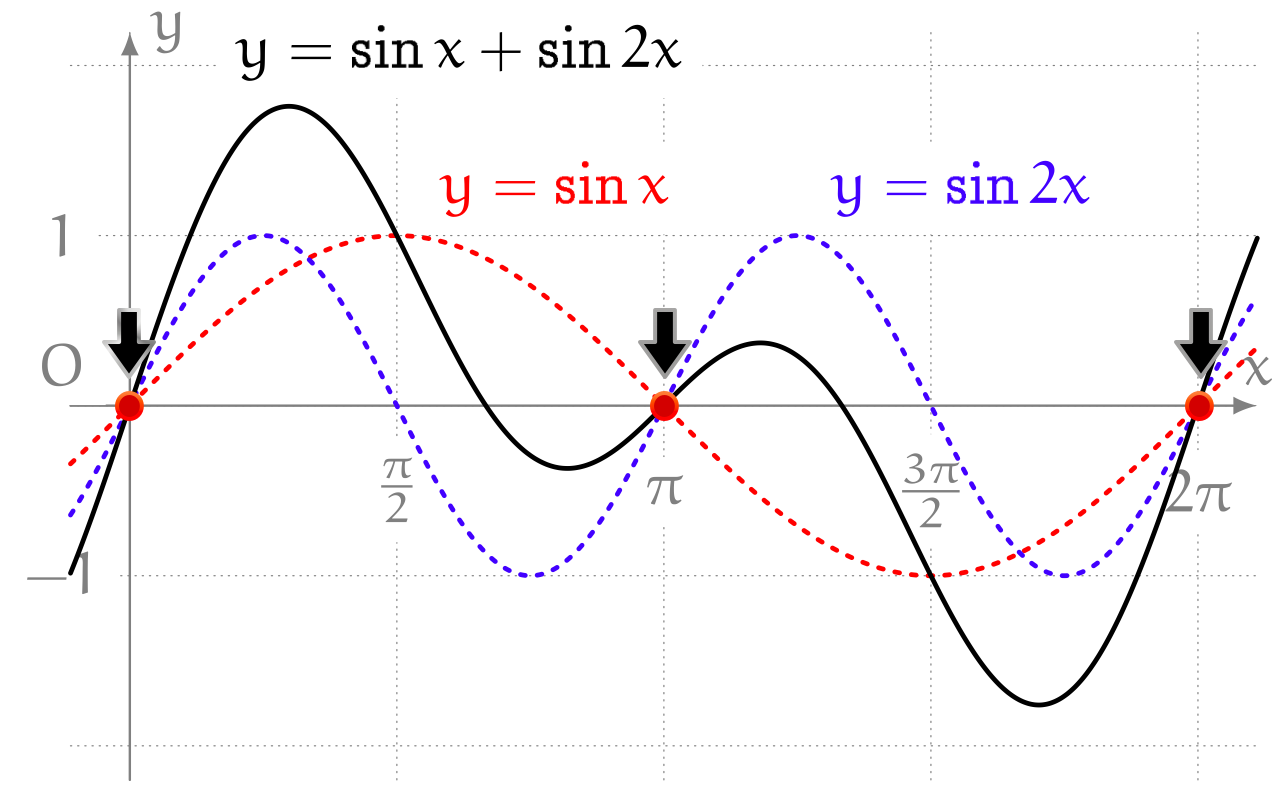
ユーリ「あ、そだね。そっか。赤と青がちょうど釣り合うところ？」

僕「そうだね。赤と青が、符号は逆で絶対値が等しくなるところがあるから、 そこでも和は $0$ になるわけだ。 $x$ がどんな値のときに和がちょうど $0$ になるかは、ちゃんと計算しないとわからないけど」

ユーリ「……」

僕「ユーリは $0$ になるところを見てたけど、お兄ちゃんはね、 一番高いところを見ていたんだよ」

ユーリ「高いところ？」

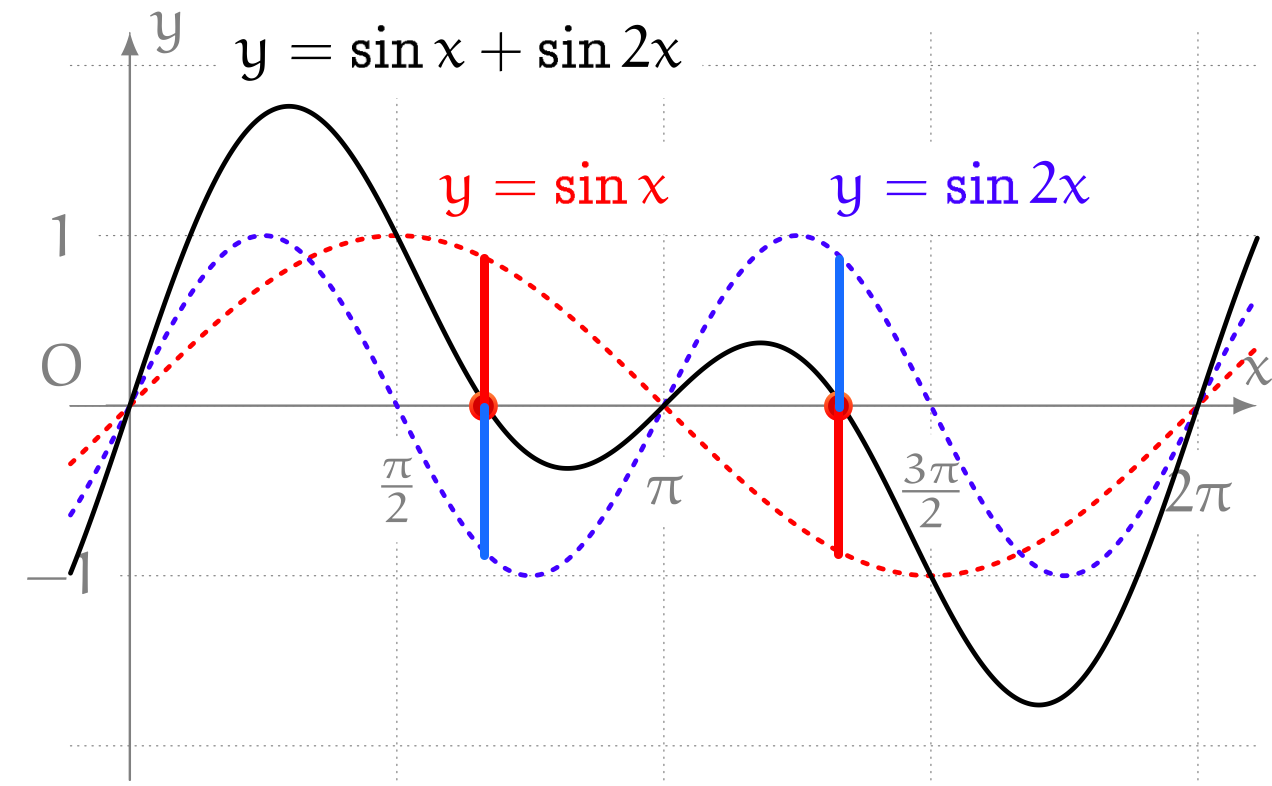
僕「ほら、 $y = \sin x$ の方も、 $y = \sin 2x$ の方も、 一番 $y$ が大きくなるところ……つまり波が高くなるところって $y = 1$ だよね。 でも、両方が重なって作る波は、 $y = 2$ にはならない。 つまり、二つの波の最大値を足したものが、重ね合わせた波の最大値にはなってないよね」

ユーリ「そりゃそーじゃん。だって、最大になるところがずれてるからでしょ？　 青い波は $x = \frac{\pi}{4}$ で最大だけど、 赤い波は $x = \frac{\pi}{2}$ で最大だから。 惜しかったねーって感じ？　二人が波長合わせてたら良かったんだけどねー……波だけに」

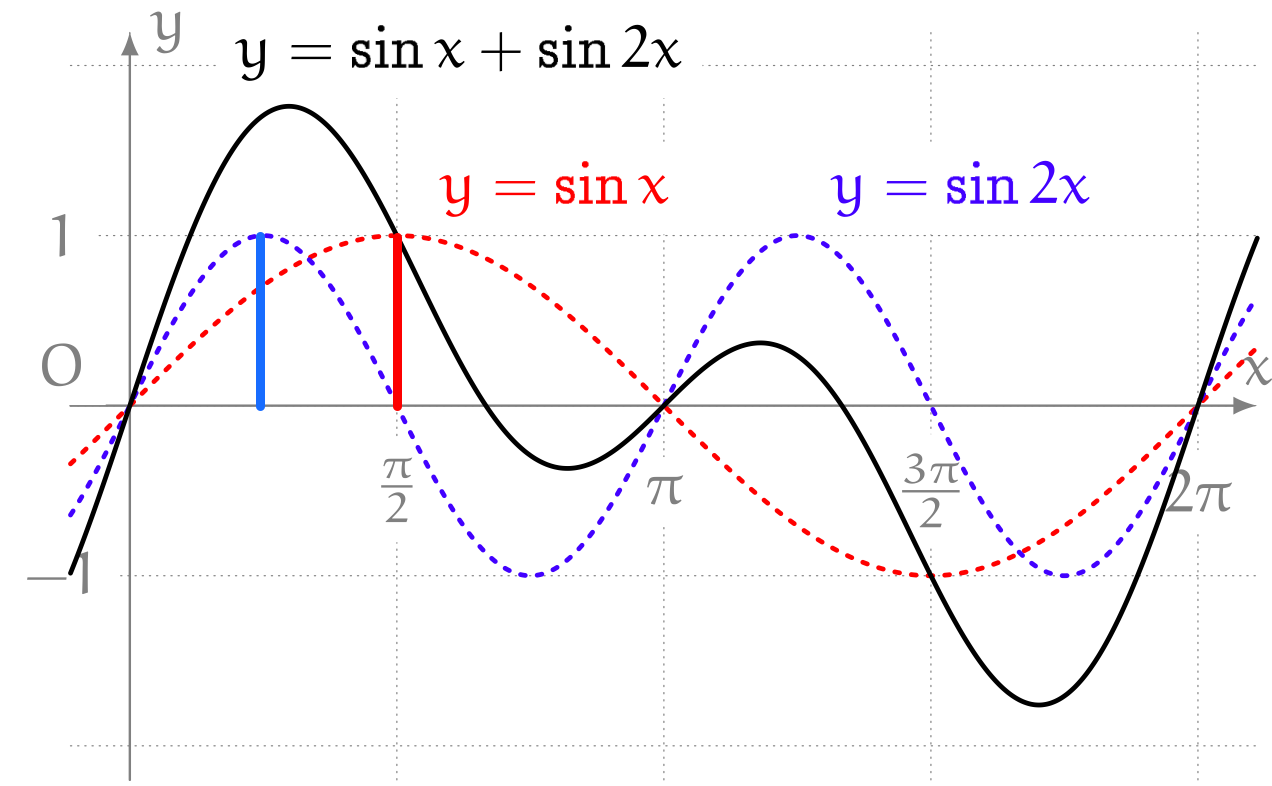
僕「なんだそれ。それから思ったことはね、対称性だよ。 いま言った最大値の重なりのずれと同じ形が、最小値の重なりのずれでも起きているよね」

ユーリ「そだね。さっきとは上下逆だけど」

僕「上下逆だし、これは $(x, y) = (\pi, 0)$ という点を対称の中心にして、 点対称になってるんだよ。ぐるっと回転させれば重なる」

ユーリ「ほほー！　なるほど」

僕「それから、対称性はあちこちにあるよ。ほら、原点のまわりも見てごらん」

ユーリ「ははーん、確かにここも点対称？」

僕「そうだね。原点を中心にぐるっと回転させれば、もとのグラフにぴったり重なる」

ユーリ「ふんふん」

僕「まあ、そのことは、 $\sin x$ と $\sin 2x$ がどちらも奇関数（きかんすう） であることからもわかるんだけどね」

ユーリ「きかんすう」

僕「そう、奇関数。サインカーブの形を見ればわかるけど、 $$ \sin (-x) = - \sin x $$ という式がどんな $x$ についても成り立つよね。 こういう関数のことを奇関数っていうんだよ」

ユーリ「また数式、出てきたし」

僕「いやいや、こんなのぜんぜん難しい話じゃないよ。 具体的に考えてみれば意味はすぐにわかる。 たとえば $x = \frac{\pi}{2}$ として考えてみると、 $$ \sin \left(-\frac{\pi}{2}\right) = -1 $$ なのに対して、 $$ -\sin\frac{\pi}{2} = -1 $$ になっているだろ？　だから確かに $x = \frac{\pi}{2}$ のときには、 $$ \sin (-x) = - \sin x $$ が成り立っている。いまは $x = \frac{\pi}{2}$ だけで試したけど、 $x$ がどんなときもこの式は成り立つ。こういう関数のことを奇関数というんだ。 $\sin x$ は奇関数の一つになる」

ユーリ「ふーん」

僕「あれ、ノリ悪いな。 たとえば $x = -\frac{\pi}{2}$ のときも同じだよ。 実際、計算してみると」

ユーリ「いやいや、計算はわかったんだけど……お兄ちゃんは、 ちゃちゃっと式を出して《ほらね、だから奇関数だろ？》みたいなこと、よく言うよね」

僕「まあ、そうかな？」

ユーリ「よく言う、よく言う」

僕「そしてユーリから数式マニアと茶化される」

ユーリ「あのね、グラフを見ながら《ぐるっと回して点対称》という説明だったらよくわかるんだけど、 式を出されて《ほらね》と言われても、うーん……って思っちゃうかなー」

僕「そう？　でもほら、ユーリは《バシッとわかる》のが好きじゃないか。 グラフの形を見てわかるのは大切だし、楽しいけど、 うるさいこと言い出すと『これって点対称に見えるけれど、 ほんとうに、ほんとうに、ほんとうに点対称なのかな』って疑問が出てこない？」

ユーリ「うっ……にゃるほど」

僕「だって、 コンピュータが描いていて正確だとしても、それを見ているのは人間の目だからね。 形がそれっぽくてだまされることもあるかも。 その点、数式と論理で証明できるなら、それのほうが《バシッとわかる》ような気がするんだけどな」

ユーリ「……」

僕「話もどすけど、 $\sin x$ も、 $\sin 2x$ も、どちらも奇関数になる。 つまり、 $$ \begin{align*} \sin (-x) &= - \sin x \\ \sin (-2x) &= - \sin 2x \\ \end{align*} $$ が成り立っている。そして、両方の和もまた奇関数になる。 だって、 $$ f(x) = \sin x + \sin 2x $$ とおいたとしたら、 $$ f(-x) = -f(x) $$ が成り立つからね。計算すればわかる。 $$ \begin{align*} f(-x) &= \sin(-x) + \sin(-2x) \\ &= -\sin(x) - \sin(2x) \\ &= -\left(\sin(x) + \sin(2x)\right) \\ &= -f(x) \\ \end{align*} $$ ね？　さらに一般化して、 $\sin nx$ という関数の和で作られる関数は、 すべて奇関数になることも証明できる。 ってことは、そのグラフはすべて原点で点対称になる！　数式を使えば、グラフを実際に描かなくても、 その形について主張ができるわけだ！　これだよ」

ユーリ「うーん……そっか……」

僕「それはそれとして、 こんなふうに波全体の形をじっくり見るのもおもしろいよ、もちろん」

ユーリ「波全体の形……」

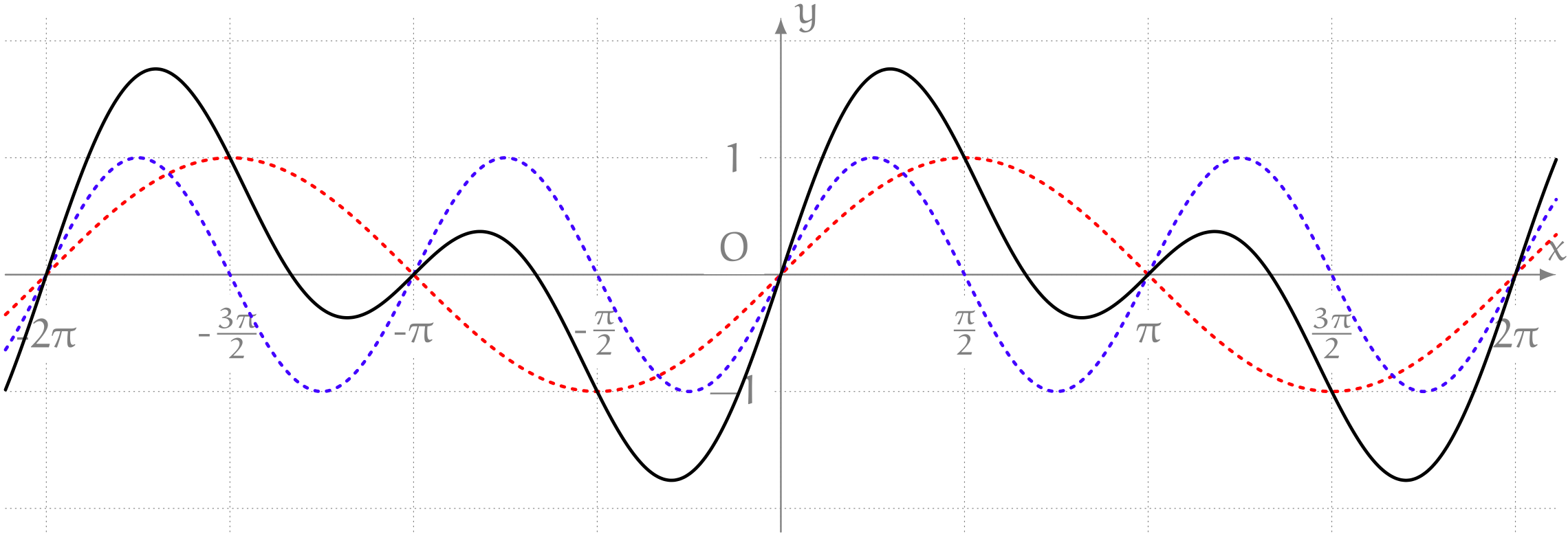
ユーリ「ねえ、お兄ちゃん。この $y = \sin x + \sin 2x$ のグラフって全体の形としては、 $y = \sin 2x$ だよね」

僕「どういう意味？」

ユーリ「だってほら、 $0$ から $\pi$ までの間に、山と谷が一回ずつあるじゃん？　 それって、 $y = \sin 2x$ と同じだもん」

僕「ああ、そうだね。 $y = \sin x$ の波と足しあわせているから、全体的にはゆがんでるけどね」

ユーリ「はっ！　お兄ちゃん！　ユーリ発見したよ！」

僕「なにを？」

ユーリ「あのね、 $$ y = \sin x + \sin 2x $$ じゃなくて、 $$ y = \sin x + \sin 3x $$ にするの。 そしたら、波はやっぱり《だいたいは $\sin 3x$ だけど、 $\sin x$ のせいで少しゆがむ》形になるんじゃない？」

僕「ほほー、それは《ユーリの予想》だね？　じゃあ、確かめてみようか。実際に、 $$ y = \sin x + \sin 3x $$ のグラフがどんな形になるのか……」