![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
ユーリ「ねー……お兄ちゃん! 何だかめんどーだよ。 お兄ちゃんってずっと数式ばっかりいじってるんだもん。 波の話じゃないの?」
僕「だから、《うなり》の話をしてるんじゃないか。 二つの波が重なるとき、周波数がちょっとずれると……」
ユーリ「だって、《うなり》なんて聞いたことないもん」
僕「そうか。ちょっと待って。ネットで検索したらきっと音源見つかるよ」
ユーリ「ネットなんて、持ち出していいの?」
僕「メタ発言自重」
僕はコンピュータで《うなり》の音源を検索した。
僕「……ほら、あったよ。最初の音源は周波数が $440$ Hz(ヘルツ)のもので、 次の音源は $441$ Hzのもの。 そして三番目の音源が両方を重ね合わせた音になっているよ。 $440$ と $441$ だから、周波数が $1$ Hzずれていて、 $1$ 秒に $1$ 回の《うなり》 が聞ける」
ユーリ「どれどれ……」
ユーリ「うっわー、 $440$ Hzと $441$ Hzの違いってビミョーだね。 でも、 $440$ Hz + $441$ Hzのは、確かにうなってる。わん、わん、わん、わん……」
僕「だから、こういう現象も数式を駆使すれば解析できるんだよ。 数式、あなどるべからず」
ユーリ「え? 話、逆じゃないの?」
僕「逆って?」
ユーリ「《うなり》の回数を調べれば、ビミョーな周波数の違いも調べられるってこと。 実験、あなどるべかる、べるからず……って」
僕「おっと。なるほど? ……確かに。正確な $440$ Hzの音Aと、ちょっとずれた音Bがあったら、 同時に鳴らして《うなり》の周波数を調べればBの周波数がわかることになるな」
ユーリ「でしょ?」
僕「でも、その調べ方でBの周波数がわかるという保証のためには、数式が必要なんだけどな」
ユーリ「ふむー……それはさておき、 せっかくコンピュータ使うんだから、波を見せてよ」
僕「そうか、そうだな……ええと、このサイトで見れるかな。 たとえば、 $y = \sin x$ というグラフはこういう形をしている」
ユーリ「知ってる知ってる。サインカーブでしょ? こないだ描いたじゃん。 波長に周期に……(第141回参照)」
僕「そうだね。物理的な波動のときは横軸が《位置》なのか、《時刻》なのか注意する必要があるね。 このグラフは物理的な話から離れて、 $x$ と $y$ の関係として $y = \sin x$ のグラフを描いてることになるよ」
ユーリ「何言ってるかわかんない」
僕「あ、いやいや、たいした話じゃない。いまは $y = \sin x$ のグラフを描いただけであって、 $x$ が何を表しているかはさておいているよ、ってこと」
ユーリ「これって、数式を書いたら自動的にグラフ描いてくれるサイト?」
僕「そうだね。 $x$ はここでは適当に $-2\pi$ から $2\pi$ くらいの範囲で描かれているけど、 ほんとうは正にも負にも無限に波は続いている」
ユーリ「無限の波は描けないけどね」
僕「確かに。ところで、ユーリは $2\pi$ って何だか知ってる?」
ユーリ「円周率の $2$ 倍」
僕「うん、だから、 $2\pi$ はただの数だよ。円周率 $\pi$ は $3.14\cdots$ だから、 $2\pi$ は $6.28\cdots$ という数になるよね」
ユーリ「? 何でそんなに当たり前のことゆーの?」
僕「ユーリには当たり前なんだ。 お兄ちゃんはね、初めて $\pi$ の話を聞いたとき、 なかなか $\pi$ がただの数とは思えなかったんだよ」
ユーリ「へんなの……他のグラフ描こうよ!」
僕「うん、じゃあね。クイズにしよう。 $$ y = \sin 2x $$ これはどんなグラフになると思う?」

ユーリ「カンタン! $\sin \heartsuit$ があったとき、 $\heartsuit$ のところは、波の数に効いてくるんでしょ? $2x$ にしたら、 波の数が $2$ 倍になるはず!(第142回参照)」
僕「そうだね。じゃ、 $y = \sin 2x$ を描いてみよう。数式を入力して、と」
ユーリ「わくわく」
ユーリ「ほーらね。ちょうど $2$ 倍になってる」
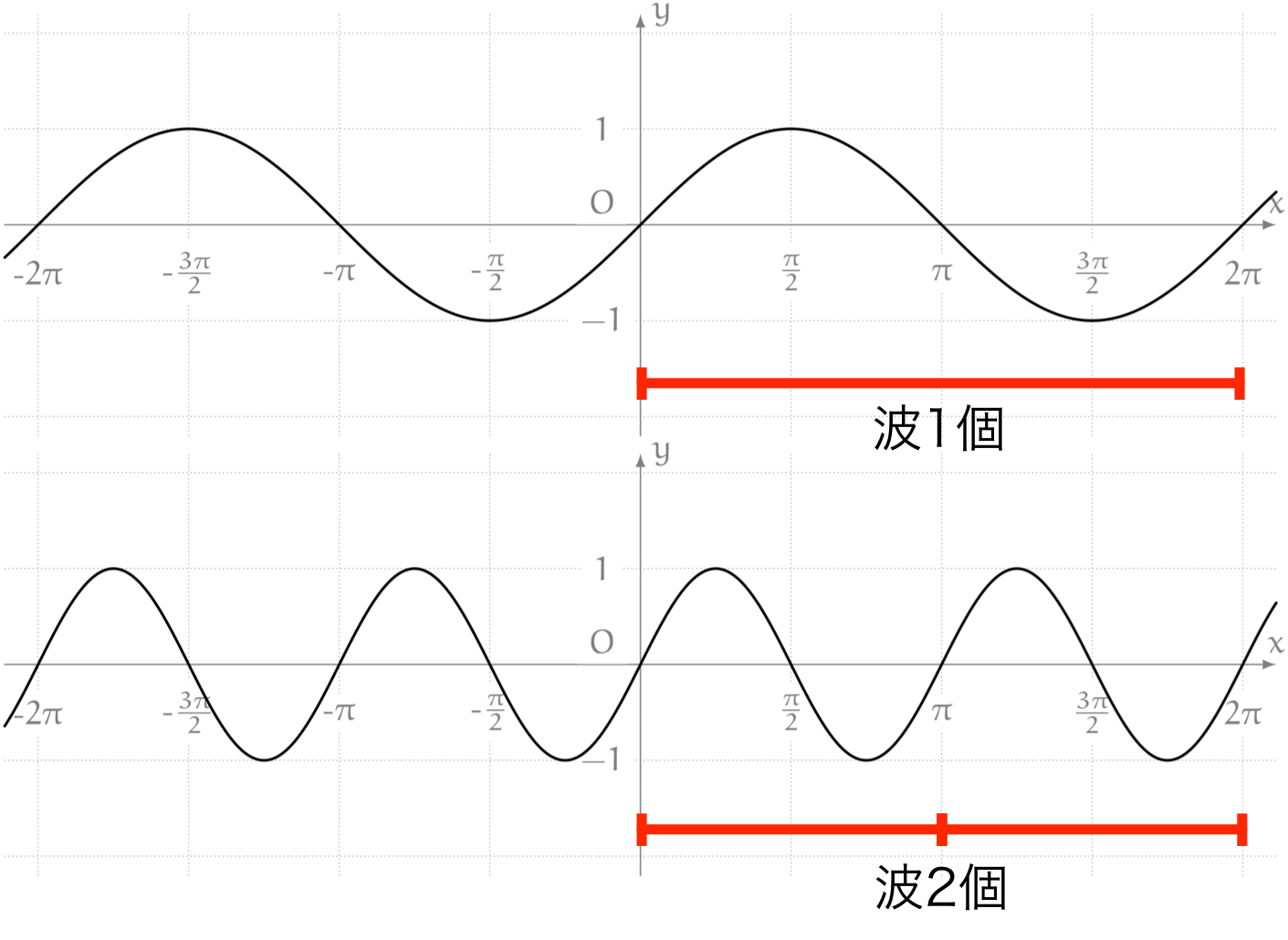
僕「うん、さっきは $0$ から $2\pi$ までで $1$ 個の波だったのが、 今度は $0$ から $2\pi$ までで $2$ 個の波になったね」
波の数を $y = \sin x$ と $y = \sin 2x$ で比較する
ユーリ「ちょっと、ユーリにも入力させてよ。 $y = \sin 3x$ なら $3$ 倍になるんでしょ?」
僕「うん、その通りになったね」
ユーリ「これ、いくらでも多くできるのかにゃ?」
僕「できるねえ」
ユーリ「お兄ちゃん、うずうずしてる?」
僕「何が?」
ユーリ「そろそろ、《一般化》したくなってるでしょ?」
僕「ああ、まあね。でもそれはかんたんにわかるよね。 $$ y = \sin nx \qquad (n = 1,2,3,\ldots) $$ というグラフを描いたら、ぜんぶサインカーブになって……」
ユーリ「そんで、 $x$ が $0$ から $2\pi$ まで動くときに波の数は $n$ 個になる」
僕「そうそう。そうなるね」
ユーリ「ねー、これってコサインのグラフも描けるの?」
僕「描いてみよう。 $y = \cos x$ を入力すると……」
ユーリ「おー、描けた」
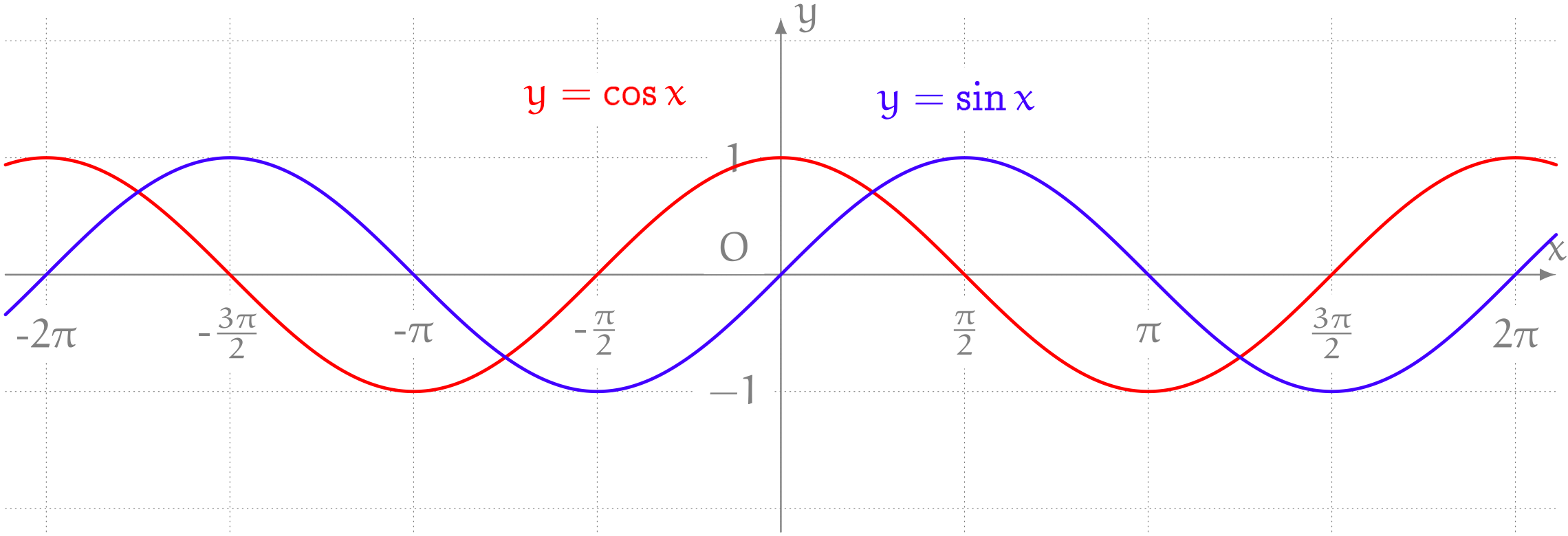
僕「$y = \cos x$ のグラフを、 $\frac{\pi}{2}$ だけ動かすと、 $y = \sin x$ のグラフと同じになるよ」
ユーリ「右に動かすんでしょ?」
$y = \cos x$ のグラフを右に $\frac{\pi}{2}$ だけ動かすと、 $y = \sin x$ のグラフになる
僕「そうそう。これはテトラちゃんにも出したクイズだけど、 $$ \begin{align*} y &= \cos\left(x + \frac{\pi}{2}\right) \\ y &= \cos\left(x - \frac{\pi}{2}\right) \\ \end{align*} $$ のどっちが、 $y = \sin x$ のグラフになると思う?」
ユーリ「えーと……この、どっちか」
僕「だから、どっちが?」

ユーリ「ちょっと待って……たぶん、 $$ y = \cos\left(x - \frac{\pi}{2}\right) $$ のほう」
僕「ファイナルアンサー?」
ユーリ「イエス、イエス」
僕「じゃ、入力してみよう。 $y = \cos\left(x - \frac{\pi}{2}\right)$ と……」
ユーリ「ほーらね!」
僕「えらいえらい。どう考えたの?」
ユーリ「なんとなく」
僕「がく。さっき、考えていたじゃないか」
ユーリ「あのね、 $\frac{\pi}{2}$ のときのこと考えたの。 引き算で $0$ じゃん。 そのとき $\cos$ は $1$ で $\sin$ も $1$ でビンゴ!」
僕「すごい説明だな」
ユーリ「でも、伝わった?」
僕「伝わったけどね。 $x = \frac{\pi}{2}$ のときのことを考えてみたと。 $x = \frac{\pi}{2}$ のとき、 $$ \begin{align*} \cos\left(x - \frac{\pi}{2}\right) &= \cos \left(\frac{\pi}{2} - \frac{\pi}{2}\right) \\ &= \cos 0 \\ &= 1 \\ \end{align*} $$ という計算で答えは $1$ になる。一方、 $$ \begin{align*} \sin x &= \sin \frac{\pi}{2} \\ &= 1 \\ \end{align*} $$ になるから、 やっぱり $1$ で等しくなるということだろう?」
ユーリ「その通りじゃ」
僕「年取るなよ。うん、それはお兄ちゃんがテトラちゃんに話したのと同じチェック方法だよ」
ユーリ「ほほー」
僕「グラフの移動は、 グラフを《右に動かす》というので《$+$ にする》と誤解しがちなんだよね。 $y = \cos\left(x + \frac{\pi}{2}\right)$ にすると、 $y = \cos x$ のグラフは左に動いてしまう」
ユーリ「ふんふん……それにしても、数式入力するとグラフ出てくるっておもしろいね」
僕「そうだね」
ユーリ「数式でグラフを作ってるみたい。数式を変えると、グラフも変わる。って、あたりまえか」
僕「楽しいよね。じゃあ、別のパターンのグラフも描いてみようか。たとえば、 $y = 2\sin x$ のグラフ」
ユーリ「そりゃそだね。 $\sin x$ を $2$ 倍したんだから、一番上は $2$ になるし、一番下は $-2$ になるけど、 $0$ は $0$ のまま。 じゃさ、 $y = 2 \sin 2x$ だと、 高さも波の数も $2$ 倍になるね」
ユーリ「ほらほら」
僕「ちゃんと予想通り描けているなあ」
ユーリ「こんなのカンタンだよ」
僕「じゃあ、今度は二つの波を考えてみようよ。 たとえば、 $y = \sin x + \sin x$ のグラフは想像がつく? 波の重ね合わせだよ」
ユーリ「どんとこい。 ……えーと、 $\sin x$ と $\sin x$ の重ね合わせ? あ、なーんだ。これもカンタン! だって、 $y = \sin x + \sin x$ ということは、 $\sin x$ の $2$ 倍ってことでしょ? さっき描いた $y = 2\sin x$ と同じ形じゃん!」
僕「気がつくか」
ユーリ「気がつくよー」
僕「じゃあ、これはどうかな? これもテトラちゃんに出した問題だけど、 $$ y = \sin x + \cos x $$ のグラフはどんな形になると思う?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2016年2月5日)
この記事は『数学ガールの物理ノート/波の重ね合わせ』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!