![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
僕とユーリはグラフが作り出す図形の面積についておしゃべりしていた(第133回参照)。 区分求積法を使って $y = x$ のグラフが作り出す三角形の面積を求めたところ。
$y = x$ が作るこの三角形の面積 $S$ は $\frac12$ に等しい

僕「区分求積法を使って三角形の面積を求めたけれど、 これは、あまりありがたみがないよね。だって面積が $\frac12$ だって最初からわかってるし」
ユーリ「なにそれいまさら」
僕「いま求めたのは《$y = x$ の直線が作った図形の面積》だったよね。 だから今度は、ちょっと難しくして《$y = x^2$ の放物線で作った図形の面積》を調べてみようよ。 これは三角形と違ってすぐに面積はわからない。 ちゃんと区分求積法で面積が定まるかどうか、考えよう」
問題
面積 $S$ を、区分求積法で求めよう。
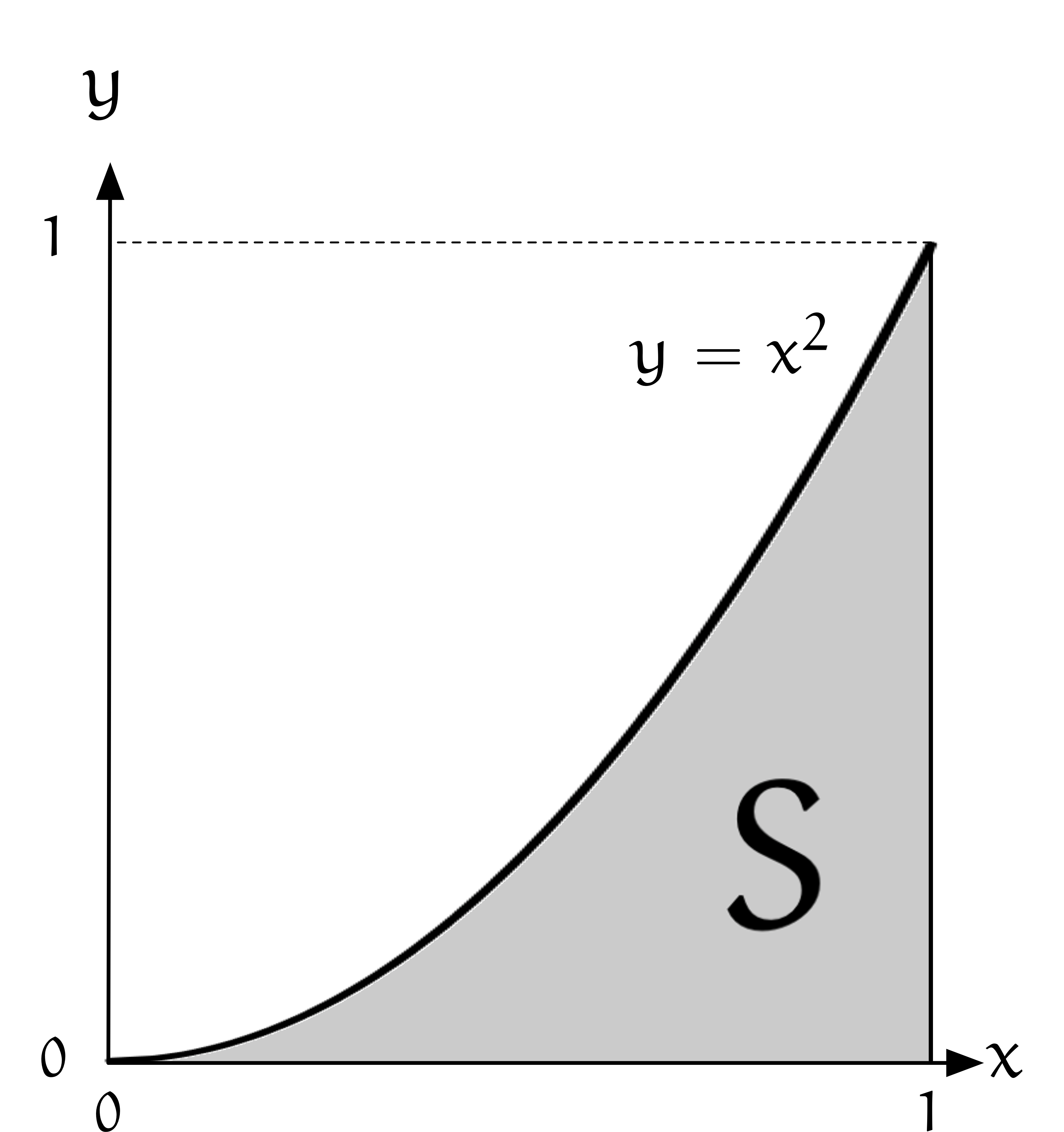
ユーリ「ほほー! これ、求められんの?」
僕「たぶんできる」
ユーリ「わかった! じゃあ、やるね。 放物線を $n$ 分割して $n$ を大きくするんでしょ? さっき(第133回参照) とおんなじにすればいーんだから、簡単だね! えーと……」
僕「いやいや、ユーリ、ちょっと待って。 さっきの三角形のときにやったことを振り返って、 注意深くやらないと」
ユーリ「だから、おんなじにするんでしょ?」
僕「いきなり $n$ 分割するんじゃなくて、こういう手順で考えていこうよ」
僕「そして、 $L_n$ と $M_n$ で、求める面積 $S$ を $L_n < S < M_n$ のように《はさみうち》するわけだね……って、 ユーリ、話聞いてる?」
ユーリ「聞いてない。すぐできるから計算してる。うわ、できそーだけどめんどくさいね」
僕「ユーリ。一歩ずつ進もうよ」
ユーリ「へーい。どこから?」
僕「$4$ 分割から」
ユーリ「はいはい。グラフは $y = x^2$ で $4$ 分割……ってこーかにゃ?」
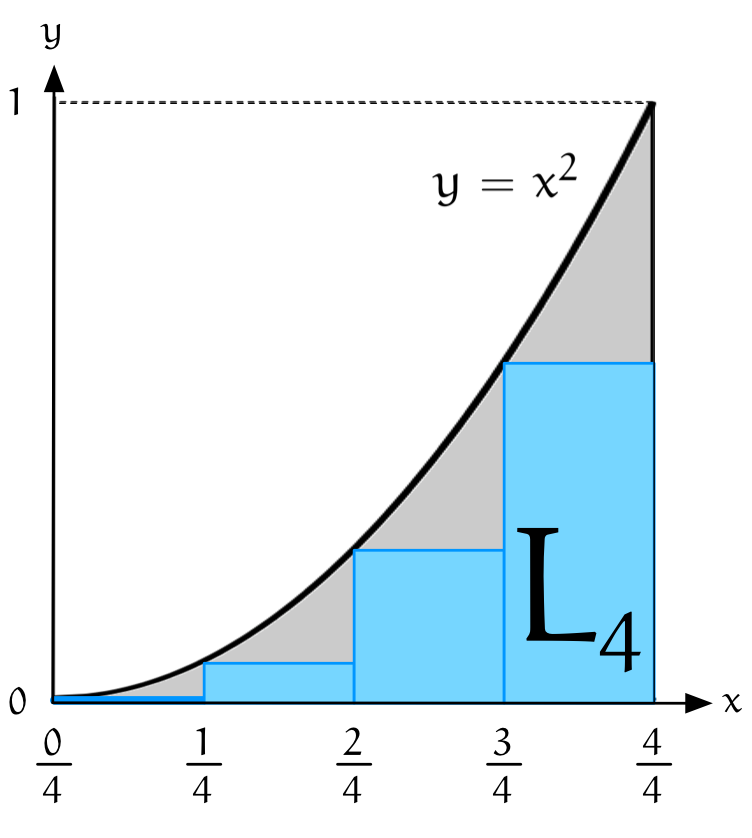
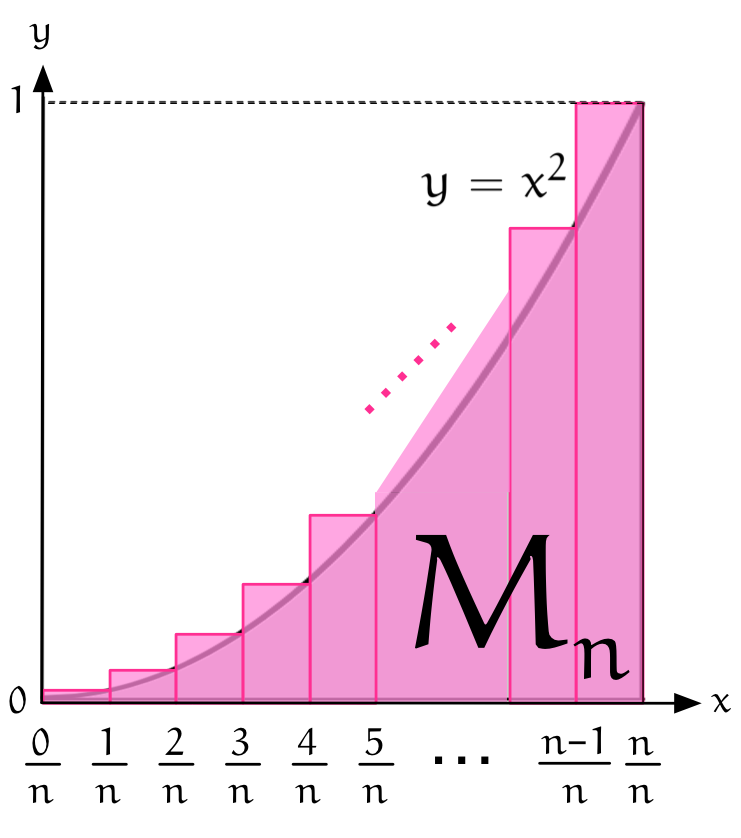
僕「そうだね。ここには $4$ 個の長方形があって……」
ユーリ「さっきとおんなじだからわかるよ! 一番左の長方形は高さが $0$ だから見えないんでしょ?」
僕「そうだね。 $4$ 個の長方形の高さはわかる? 左端は $0$ だね」
ユーリ「えーと……わかる。このグラフは $y = x^2$ で二乗すればいーから、 $\frac0{16}, \frac1{16}, \frac4{16}, \frac9{16}$ でしょ?」
僕「そうなるね。ユーリは計算しちゃったけど、長方形の高さはこうだ」
$$ \frac{0^2}{4^2}, \frac{1^2}{4^2}, \frac{2^2}{4^2}, \frac{3^2}{4^2} $$ユーリ「だから、それを計算したんだけど? あーあれかー! 計算しないほうがわかるってやつ?」
僕「そうそう。どうせ後から $n$ 分割するんだから、それを見越して式を組み立てておくんだよ」
ユーリ「ふんふん」
僕「いまのが長方形の高さ、つまり縦の長さ。じゃ、長方形の幅は?」
ユーリ「$4$ 分割だから、 $\frac14$」
僕「そうだね。これで、 $L_4$ の式が立てられる」
$y = x^2$ の下に敷き詰めた $4$ 個の長方形、その面積の和 $$ \begin{align*} L_4 &= \frac14\cdot\frac{0^2}{4^2} + \frac14\cdot\frac{1^2}{4^2} + \frac14\cdot\frac{2^2}{4^2} + \frac14\cdot\frac{3^2}{4^2} \\ &= \frac1{4^3}\left(0^2 + 1^2 + 2^2 + 3^2\right) \\ &= \frac1{64}\left(0 + 1 + 4 + 9 \right) \\ &= \frac{14}{64} \\ &= \frac{7}{32} \\ \end{align*} $$
ユーリ「あれ、やっぱりお兄ちゃんも計算してるじゃん」
僕「うん。さっきの三角形と違って、 僕たちは答えを知らないから、注意して進まなきゃいけないんだ」
ユーリ「結局 $L_4$ はこーでしょ?」
$L_4$ が求められた

$$ L_4 = \frac1{4^3}\left(0^2 + 1^2 + 2^2 + 3^2\right) = \frac{7}{32} $$
ユーリ「$M_4$ もすぐできるね。さっきとそっくり」
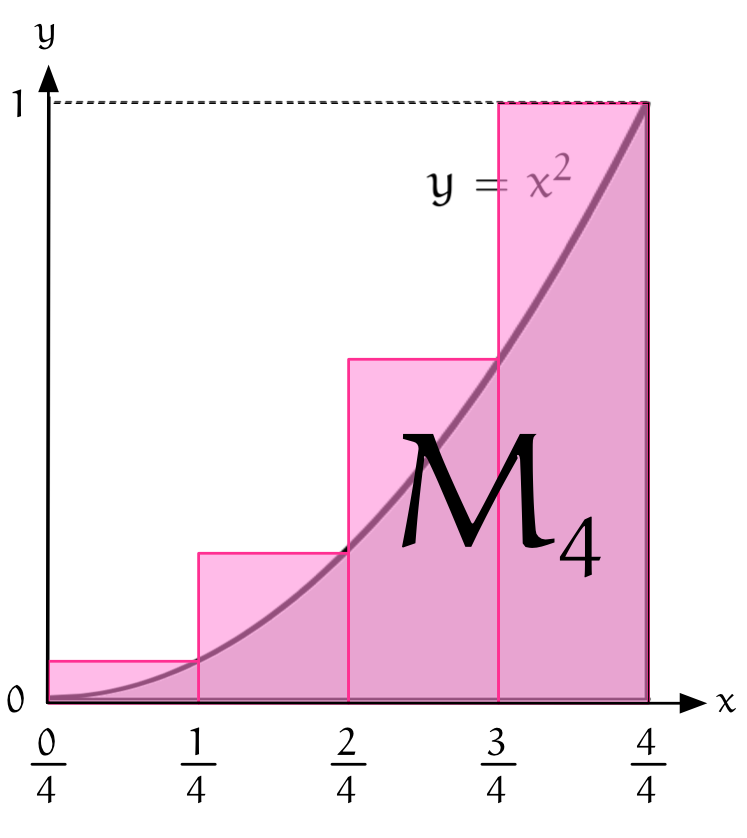
僕「うん、同じように考えるけど、 $L_4$ のときと高さが違うから、そこだけ注意がいるね」
$y = x^2$ の上を覆う $4$ 個の長方形、その面積の和 $$ \begin{align*} M_4 &= \frac14\cdot\frac{1^2}{4^2} + \frac14\cdot\frac{2^2}{4^2} + \frac14\cdot\frac{3^2}{4^2} + \frac14\cdot\frac{4^2}{4^2} \\ &= \frac1{4^3}\left(1^2 + 2^2 + 3^2 + 4^2\right) \\ &= \frac1{64}\left(1 + 4 + 9 + 16 \right) \\ &= \frac{30}{64} \\ &= \frac{15}{32} \\ \end{align*} $$
$M_4$ が求められた

$$ M_4 = \frac1{4^3}\left(1^2 + 2^2 + 3^2 + 4^2 \right) = \frac{15}{32} $$
僕「これで、 $L_4$ と $M_4$ ができた。じゃ、いったん整理しよう」
$4$ 分割したときの長方形の面積の合計($y = x^2$)
$$ \left\{\begin{array}{llll} L_4 &= \frac1{4^3}(0^2 + 1^2 + 2^2 + 3^2) && \REMTEXT{(小さい方)} \\ M_4 &= \frac1{4^3}(1^2 + 2^2 + 3^2 + 4^2) && \REMTEXT{(大きい方)}\\ \end{array}\right. $$
ユーリ「……」
僕「どうした?」
ユーリ「なるほどにゃあ……三角形のときも、お兄ちゃんは、こーやってまとめてたけど、 $n$ に変えるトコロがすぐにわかるね!」
僕「そうなんだよ」
$n$ 分割したときの長方形の面積の合計
$$ L_n = \frac1{n^3}\left(0^2 + 1^2 + 2^2 + \cdots + (n-1)^2 \right) \qquad \REMTEXT{小さい方} $$
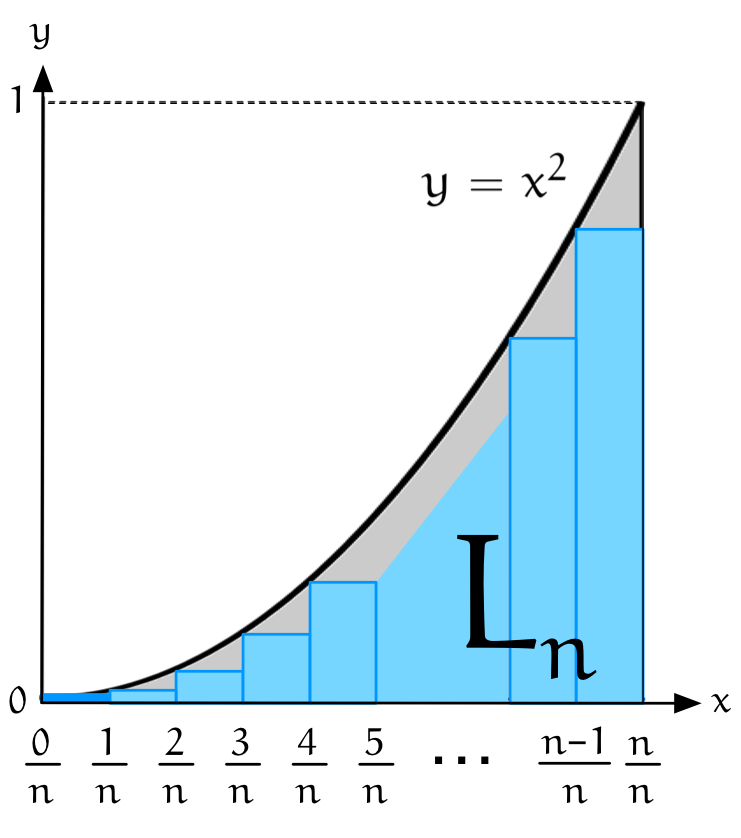
$$ M_n = \frac1{n^3}\left(1^2 + 2^2 + 3^2 + \cdots + n^2 \right) \qquad \REMTEXT{大きい方} $$
ユーリ「あ、でも、ユーリ、こんなふうになりそーだな、っては思ったよ」
僕「こんなふうとは?」
ユーリ「いや、だから、 $0^2 + 1^2 + 2^2 + \cdots + (n-1)^2$ みたいに、 $0$ の二乗、 $1$ の二乗……を足していく式が出てくるってこと。 だってほら、グラフが $y = x^2$ だから」
僕「ユーリ、それはすごいよ。式の観察力だね。 単に手を動かして計算して終わりじゃなくて、 どういう式になるだろうかって考えるのはとても大事なんだよ」
ユーリ「でも勝手に作っちゃダメでしょ?」
僕「もちろん、自分の勝手な想像で『こういう式になるだろう』と立てて結論にしちゃだめだよ。 ちゃんと理由を考えて式を組み立てる必要はある。 でも、予想するのは悪くない。なぜかというと、 計算して出た式が予想とあってるかどうか、チェックできるから」
ユーリ「ほほー」
僕「さてと。三角形のときには $1 + 2 + 3 + \cdots + n$ が必要になって求めたよね。 でも今度の放物線では $1^2 + 2^2 + 3^2 + \cdots + n^2$ を計算する必要が出てきた。 つまり、こんなクイズを解く必要がある」
クイズ
$$ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \REMTEXT{?} $$
(ただし、 $n$ は $1$ 以上の整数とする)
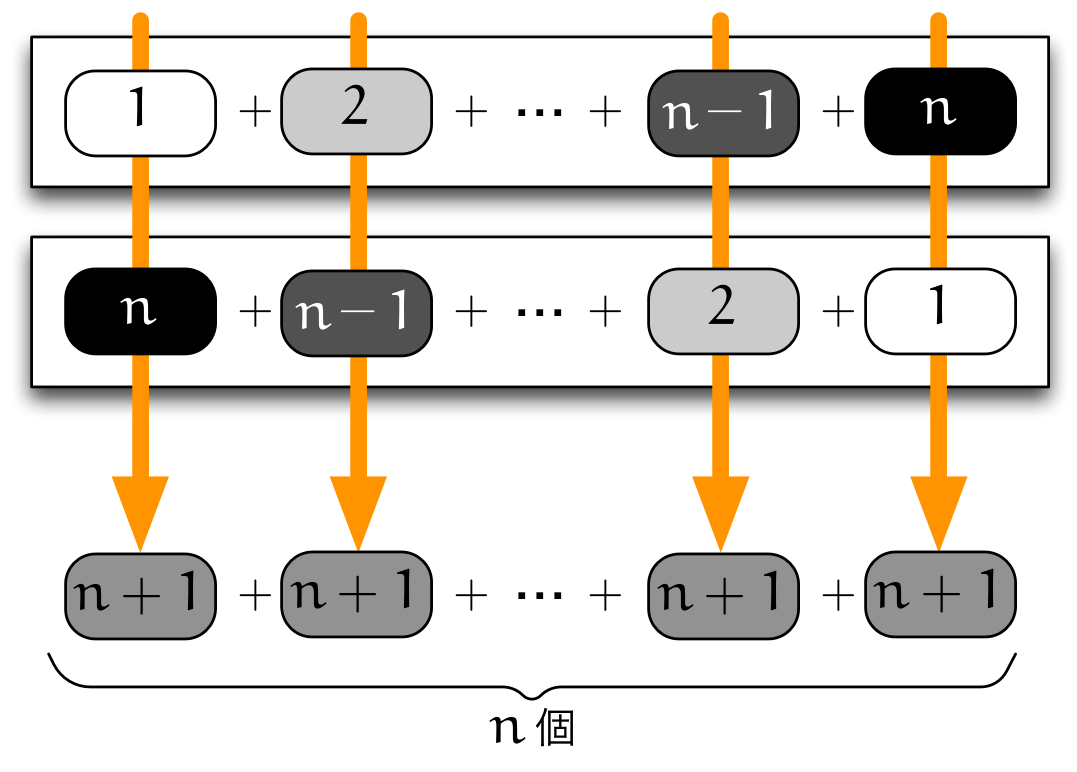
ユーリ「うんうん。これも、 $1 + 2 + 3 + \cdots + n$ のときと同じようにして、 逆順にして足せばいーんだね! $n^2 + 1$ が $n$ 個集まって $2$ で割るから、こーだね!」
ユーリの答え(?)
$$ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \dfrac{n(n^2+1)}{2} \qquad \REMTEXT{(?)} $$
僕「そうはいかないよ、ユーリ。 逆順にして加える方法は今度は使えない。 逆順にして加える方法がうまくいったのは、 縦に足したとき、全部同じ値になったからなんだから」
ユーリ「あ、そっか……え、じゃあ、どーやって求めるの?」
僕「うん、こういう問題を考えるときに大事なのは、 具体的に考えてみることだね」
ユーリ「?」
僕「つまりね、いま求めたい $1^2 + 2^2 + 3^2 + \cdots + n^2$ を考えるときに、 《小さな数で考える》ということだよ」
ユーリ「さっき、 $4$ で考えた」
僕「うん、そうだね。あれは $n = 4$ のときの $L_n$ と $M_n$ を考えたわけだ。 いまから考えたいのは、 $1^2 + 2^2 + 3^2 + \cdots + n^2$ の式で $n = 1, 2, 3, 4, 5$ くらいで実際に計算してみることだよ」
ユーリ「何だか《具体的に計算しろ》っていったり、 《途中で計算やめろ》っていったり、いそがしいにゃ」
僕「あはは、そうだね。確かに。 お兄ちゃんが言いたいのは、使える道具は何でも使い、 できることは何でもやってみるってことだよ。 数学を考えているとき、決まり切ったルールだけに縛られるのはもったいない。 解法の暗記ばかりじゃつまらない。そうじゃなくて、 自分の持っている《武器》……これはテトラちゃんがよく言うたとえだけど……《武器》 を何でも使う態度が大事なんだ」
ユーリ「テトラさん、何気にゲーム好きだよね」
僕「でね、数学を考えるときに、 自分が持っている道具に何があるのかを忘れてしまうことがある。 それで行き詰まってしまう。 $n$ が出てきたら《小さな数で考える》というのは、 武器を思い出すための工夫なんだ。 ポリヤの問いかけもそうだよね。《定義にかえれ》《与えられているものは何か》《求めるものは何か》 っていう問いかけは、自分が考えを進めるためのきっかけとなる。 それは、自分が持っている《数学に立ち向かう武器》を思い出すことなんだよ」
ユーリ「武器を手に持ってるのに、使うの忘れて敵にやられたら、ヤだね」
僕「そうだね。ということで、《具体的に計算しよう》も《途中で計算を止めて式の形を見る》も、 それぞれに大事な武器なんだ」
ユーリ「おー、先生トーク!」
僕「ちゃかすなよ。じゃあ、 $1^2 + 2^2 + 3^2 + \cdots + n^2$ でやってみよう」
ユーリ「うん!」
僕「できた?」
《$1^2 + 2^2 + 3^2 + \cdots + n^2$》
$$ \begin{array}{lll} 1^2 &= 1 &= 1 \\ 1^2 + 2^2 &= 1 + 4 &= 5 \\ 1^2 + 2^2 + 3^2 &= 1 + 4 + 9 &= 14 \\ 1^2 + 2^2 + 3^2 + 4^2 &= 1 + 4 + 9 + 16 &= 30 \\ 1^2 + 2^2 + 3^2 + 4^2 + 5^2 &= 1 + 4 + 9 + 16 + 25 &= 55 \\ \end{array} $$
ユーリ「できたけど……結果は、 $1, 5, 14, 30, 55$ だよ。さっぱりわかんにゃい。だめじゃん」
僕「数列の問題になってきたね」
ユーリ「数列……あっ! わかった! 階差数列を作るんだ!」
階差数列を作ってみる

僕「……」
ユーリ「やった! 階差数列は、 $4, 9, 16, 25$ になった。これって、二乗した数だね!」
僕「うん、平方数ともいうね。でも……」
ユーリ「でも? あ。そっか。当たり前じゃん! 二乗した数を足したんだから、 階差数列とったら、二乗した数に戻るか……」
僕「そうなるねえ」
ユーリ「うー。だめだったか……お兄ちゃん、ヨユーで構えてるけど、 ちゃんと考えてる?」
僕「この答えは暗記してるからなあ……」
ユーリ「え、なにそれずるい」
僕「あ、でもね。すごくおもしろい話があるんだよ。この二乗の和を求める方法」
ユーリ「また、数式マニア的な何かが始まるの?」
僕「ジト目禁止。そういう話じゃなくて、ミルカさんから聞いたおもしろい話があるんだ」
ユーリ「ミルカさまから? 教えて教えて!」
僕「いま僕たちは $1^2 + 2^2 + 3^2 + \cdots + n^2$ を計算したい。 《小さな数で考える》という方法はうまくいかなかった。 では、今度はポリヤの問いかけ《似た問題を知らないか》を試してみよう」
ユーリ「さっき試したじゃん。 $1 + 2 + 3 + \cdots + n$ の方法は使えなかったよ」
僕「うん、そうだね。だから、別の問題を考える。 僕がミルカさんから聞いたのは、こういう《似た問題》なんだ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年10月23日)
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!