![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
僕とユーリはグラフが作り出す図形の面積についておしゃべりしていた(第132回参照)。 母からの《おやつコール》で中断していた数学トークが再開する。
ユーリ「クッキーおいしかったね! ……何してんの?」
僕「さっきのこと、考えてたんだよ。ほら、これの話」
どうやって面積を求めればいい?

ユーリ「そーだった。長方形を使っても、 スキマ空いてるから、 面積は正確に求められないよね」
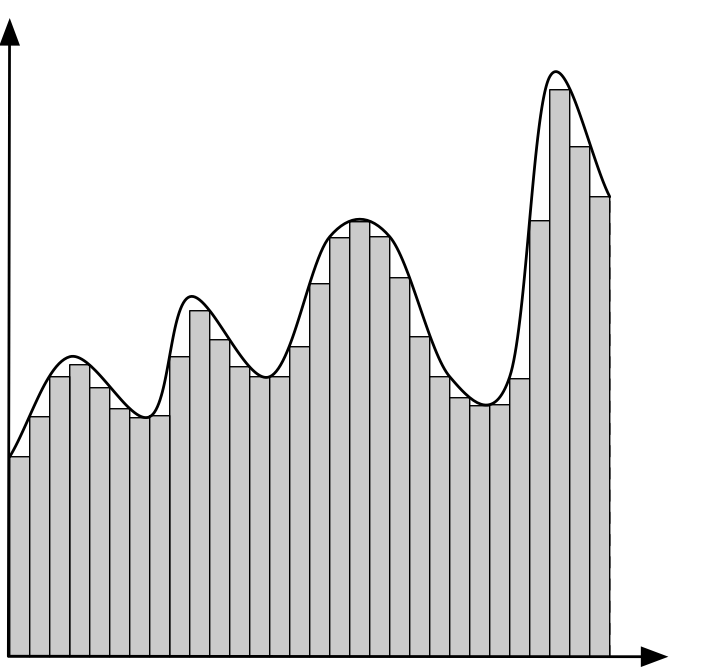
僕「その通りだね。長方形が一つだったら面積は《掛け算》すれば求められる。 長方形がいくつか並んでいたならそれを全部《足し算》すれば求められる。 でも、こんなふうにグラフが曲線になっていたら、 いくら長方形を並べても正確には求められない」
ユーリ「それじゃ、おもしろくない……そんで? 何かワザがあるっていってたじゃん。必殺技?」
僕「うん、高校で習う極限(きょくげん)を使うんだよ」
ユーリ「きょくげん……といえば」
僕「といえば?」
ユーリ「紫木一姫とか市井遊馬とか」
僕「それは字が違う……急に戯言シリーズを持ち出すなよ」
ユーリ「へへ」
僕「まじめにいこう。 たくさんの長方形を使って面積を求めるんだけど、 正確に求めるために《長方形の幅をできるだけ小さくする》ということをやりたいんだ」
ユーリ「ほほー」
僕「長方形の幅を小さくすれば、実際の面積に近づくからね」
長方形の幅を小さくすると、実際の面積に近づく

ユーリ「むむむ? ねーお兄ちゃん、これ円周率のときにやったよね!」
僕「円周率?」
ユーリ「ほらほら! 円周率を《数えて求める》話のとき。 誰だっけ、ピタゴラスだっけ」
僕「ああ、アルキメデスだね。アルキメデスが正 $96$ 角形を作って円の面積を求めようとした話」
ユーリ「そのときにも、だんだん細かくしたよ!」
僕「そうだね。その通りだ。あのときは、 正 $6$ 角形→正 $12$ 角形→正 $24$ 角形→正 $48$ 角形→正 $96$ 角形と変えたよね。 これから始める計算も、それと似た話になるよ」
ユーリ「円周率 $3.14$ まで行くの、すんごく大変だった。おもしろかったけど」
僕「おもしろかったよね」
僕「メタ発言禁止」
ユーリ「気にしない、気にしない。そんで? どーやって面積求めるの?」
僕「具体的に考えてみよう。やさしいところで、こんな三角形の面積 $S$ を求める」
この三角形の面積 $S$ を《たくさんの長方形》を使って求めてみよう。

ユーリ「すぐわかるよ! 底辺×高さ÷ $2$ だから、 $1\times1\div2 = \frac12$ で、 $S = \frac12$ だ!」
僕「そうだね。確かに $S$ の値はそうなる。 で、それを長方形を使って求めてみようということ。 $4$ 個の長方形が見えるかな?」

ユーリ「$3$ 個しか見えない」
僕「一番左の長方形は高さが $0$ だから見えないけど、長方形の一種だと思ってみよう。 そうすると、この長方形 $4$ 個はぜんぶ幅が $\frac14$ であることがわかる」
ユーリ「$4$ 等分したから、そーだね」
僕「そして高さはどうなっているかというと……」
ユーリ「$0$ と $\frac14$ と $\frac12$ と $\frac34$ になってる」
僕「その通り。それで正しいんだけど、パターンがよく見えるように約分しないで書くと、 長方形 $4$ 個の高さは…… $$ \dfrac04, \dfrac14, \dfrac24, \dfrac34 $$ となるのがわかるね」
ユーリ「ふんふん。わかるわかる。分子が $0,1,2,3$ になるって言いたいんでしょ?」
僕「そう。 この、三角形の下にある長方形 $4$ 個の面積を $L_4$ と表すことにしよう」
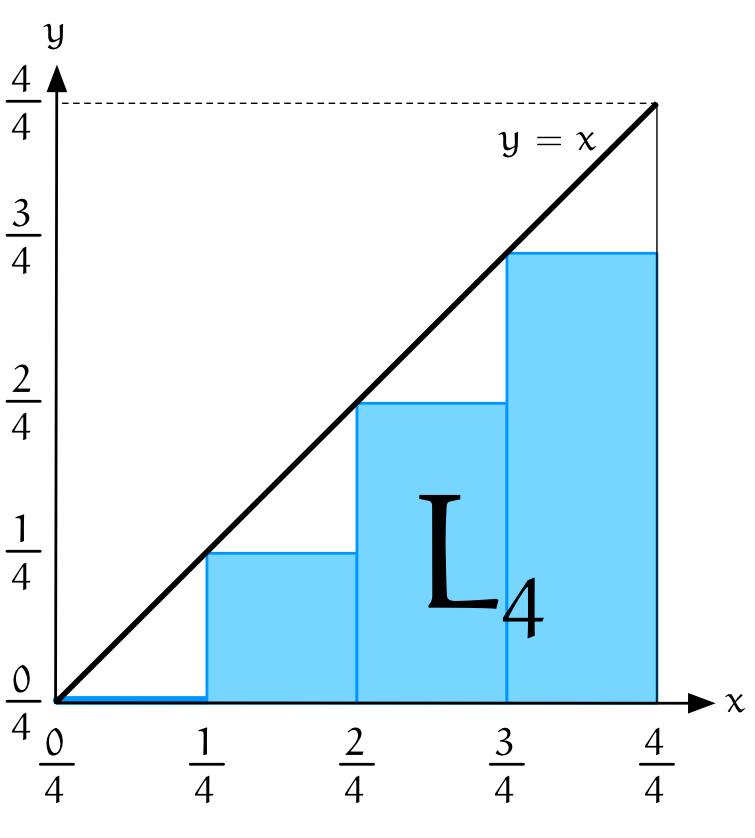
僕「そうすると、長方形の幅が $\frac14$ であることに注意して…… $$ \begin{align*} L_4 &= \frac14\cdot\frac04 + \frac14\cdot\frac14 + \frac24\cdot\frac14 + \frac34\cdot\frac14 \\ &= \frac1{4^2}(0 + 1 + 2 + 3) \end{align*} $$ になる」
ユーリ「わかる! 計算すれば、 $\frac{0+1+2+3}{16} = \frac{6}{16} = \frac38$ になる。 これって、三角形の面積 $\frac12$ より小さいね。 $\frac12$ は $\frac48$ だもん」
僕「ああ、そうだね。そういうふうに確かめるのはとてもいいね! でも、実は《計算しない》ほうが役に立つこともあるんだ。 つまり、 $$ L_4 = \frac1{4^2}(0 + 1 + 2 + 3) $$ のまま、いったん置いておく」
ユーリ「もっと計算できるのに?」
僕「もっと計算できるのに。 なぜかというと、 いまは《$4$ 分割したときの長方形の面積の合計》を求めているんだけど、 ほんとうに求めたいのは《$n$ 分割したときの長方形の面積の合計》なんだよ」
ユーリ「えぬぶんかつ」
僕「そう。《文字の導入による一般化》だね。長方形の個数を文字 $n$ で表したい。 その準備として、まずは $4$ 分割している。 だから、面積の合計を表す式の《どこに $4$ が出てくるか》がはっきり見えたほうがいいんだ。 なので、《計算しない》ほうが役に立つことがある」
ユーリ「ほほー! ……そんならそーと、先に言ってよね!」
僕「はいはい。三角形の面積 $S$ は $\frac12$ だと僕たちは知っているんだけど、 ちょっと《知らないふり》をしよう。 そして、いま、長方形を $4$ 個、そのうち $1$ 個は面積が $0$ だけど、並べた面積 $L_4$ と比較すると…… $$ L_4 < S $$ ……という式が成り立つことがわかる。わかる?」
$L_4 < S$ が成り立つ
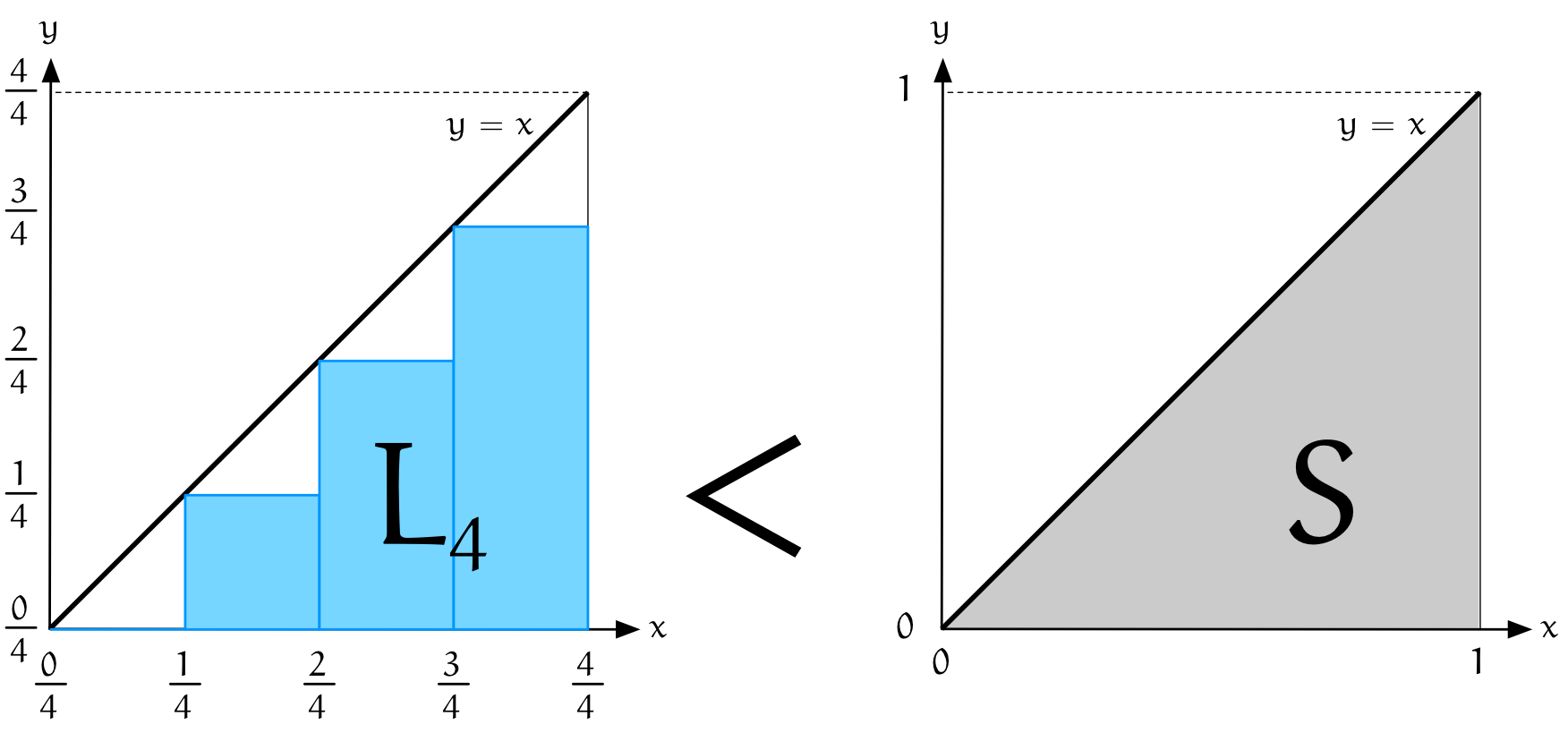
ユーリ「うん、わかる」
僕「ではもう一度 $4$ 分割しよう。今度は《上から押さえる》ようにする。 つまり、三角形を覆い隠すように長方形を並べて、 $S$ よりも大きな面積にしようというわけ。 図に描くとこうだよ」
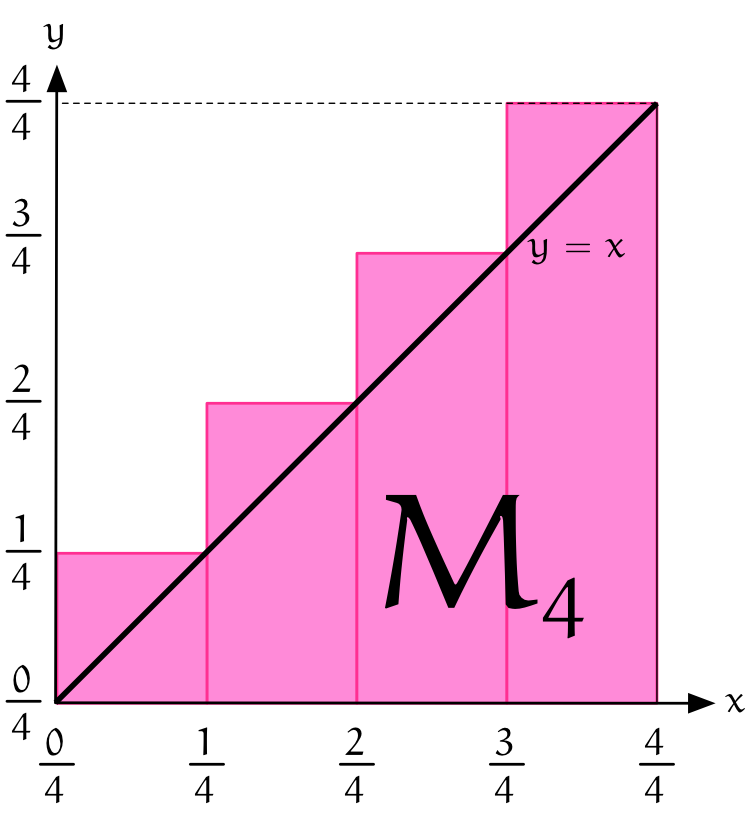
ユーリ「うん、アルキメデスの方法と同じで、《はさみうち》をするんだね!」
僕「そういうこと。三角形を覆い隠すように描いた $4$ 個の長方形の面積の合計を $M_4$ と書くことにしよう。 そうすると、 $$ L_4 < S < M_4 $$ が成り立つことがわかるよね」
ユーリ「うん、わかるわかる」
$L_4 < S < M_4$ が成り立つ
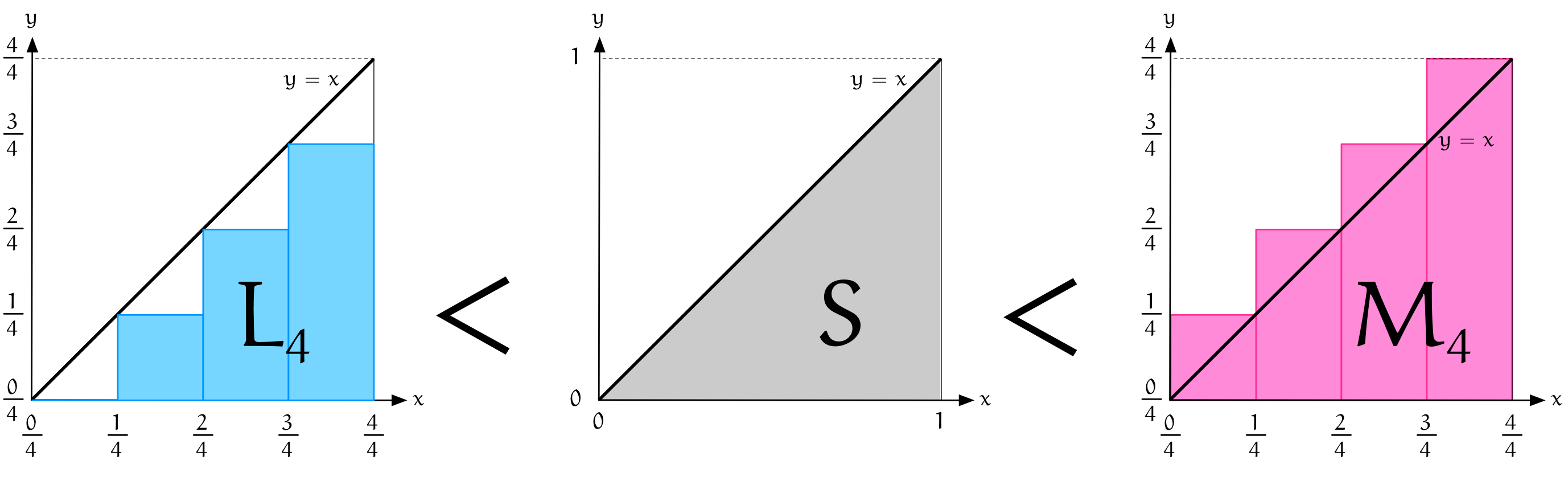
僕「じゃ、 $M_4$ は具体的に計算できる?」
問題
$4$ 個の長方形の面積の合計 $M_4$ を求めよう。 計算結果だけではなく、パターンがわかりやすい式も作ろう。

(あなたも考えてみましょう!)
ユーリ「簡単だよ!」
解答
長方形の幅は $\frac14$ で、高さは $\frac14,\frac24,\frac34,\frac44$ なので、 $$ \begin{align*} M_4 & = \frac14\cdot \frac14 + \frac14\cdot\frac24 + \frac14\cdot\frac34+ \frac14\cdot\frac44 \\ & = \frac1{4^2}(1+2+3+4) \\ & = \frac{10}{16} \\ & = \frac{5}{8}\\ \end{align*} $$ となる。
計算結果は、 $$ M_4 = \frac{5}{8} $$ で、パターンがわかりやすい式はたとえば、 $$ M_4 = \frac1{4^2}(1+2+3+4) $$ となる。
僕「いいね! 確かに、 $$ L_4 < S < M_4 $$ が成り立ってる」
僕「これで、 $L_4 < S < M_4$ という準備ができた。 ここから《文字の導入による一般化》をするんだけど、式をまとめておくよ」
$4$ 分割したときの長方形の面積の合計
$$ \left\{\begin{array}{llll} L_4 &= \frac1{4^2}(0 + 1 + 2 + 3) && \REMTEXT{(小さい方)} \\ M_4 &= \frac1{4^2}(1 + 2 + 3 + 4) && \REMTEXT{(大きい方)}\\ \end{array}\right. $$
ユーリ「お兄ちゃんってよくこういうまとめをするよね。ちゃちゃっと先に進めば早いのに」
僕「いったんまとめておくと、読みまちがいや考えまちがいを減らせるからなんだよ。 ……で、この $4$ を $n$ に置き換える。それから、「小さい方」に出てくる $3$ は $n-1$ に置き換える。 $n$ 分割すると、こういう式になるはずだよ」
$n$ 分割したときの長方形の面積の合計
$$ L_n = \frac1{n^2}\left(0 + 1 + 2 + \cdots + (n-1) \right) \qquad \REMTEXT{小さい方} $$

$$ M_n = \frac1{n^2}\left(1 + 2 + 3 + \cdots + n \right) \qquad \REMTEXT{大きい方} $$

ユーリ「にゃるほど。 $\frac1{n^2}$ に掛けるものが違う。《$0$ から $n-1$ まで足したの》と、 《$1$ から $n$ まで足したの》。確かに $M_n$ のが大きいね」
僕「ところでユーリは $1$ から $n$ まで足したらいくらになるか知ってる?」
クイズ
$$ 1 + 2 + 3 + \cdots + n = \REMTEXT{?} $$
(ただし、 $n$ は $1$ 以上の整数とする)
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年10月16日)
この記事は『数学ガールの秘密ノート/積分を見つめて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!