![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/やさしい統計』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
僕「ユーリ、何だかうれしそうだね」
ユーリ「えっへへ、わかる?」
僕「何となくね。にやにやしているから」
ユーリ「にやにやじゃなく、にこにこなんだけどなー」
僕「何かいいことあったの?」
ユーリ「んー、たいしたことじゃないけど。こないだの期末の結果」
僕「ああ、期末テスト。点数よかったの?」
ユーリ「まーね。今日、 $5$ 科目で最後の数学が返ってきて、 $100$ 点だった!」
僕「$100$ 点はすごいな……念のために聞くけど、 $100$ 点満点のテストなんだよね?」
ユーリ「その質問、ひっどいなー! $100$ 点満点だよー。 今回、他の $4$ 科目わるかったから、ギリで助かった」
僕「数学 $100$ 点のおかげで平均点もアップしたんだね」
ユーリ「そーだよ。数学のおかげで平均が $5$ 点もアップした!」
僕「なるほど……ユーリの期末テストは $5$ 科目平均が $80$ 点か」
ユーリ「んんんんんっ!? ちょっと待ったぁ!」
僕「え? 違った?」
ユーリ「何でお兄ちゃんがユーリの平均点知ってんの?」
僕「知ってるのって……」
ユーリ「誰から聞いたのっ?」
僕「……ユーリから」
ユーリ「言ってないもん! ユーリは『平均が $5$ 点上がった』って言っただけじゃん! $5$ 科目の平均点なんて言ってないもん!」
僕「計算すればすぐわかるよ」
ユーリ「はああ?」
僕「つまり、こんな問題を解いたんだね」
問題(平均点を求める)
ユーリは $100$ 点満点のテストを $5$ 科目受験した。
ユーリが最後に受けた数学の点数は $100$ 点で、これによって、平均点は $5$ 点上がった。
ユーリの $5$ 科目平均点を求めよ。
(あなたも、考えてみましょう!)

ユーリ「いやいやいや、問題形式にしなくていいから!」
僕「簡単に解けるだろ?」
ユーリ「そっか……確かに解けるね。うー、不覚不覚! 数学 $100$ 点で平均点 $5$ 点上げたから、 $4$ 科目で $20$ 点分になって、 $5$ 科目平均は $100$ 点から $20$ 点引いて $80$ 点ってバレちゃうのか……うわー」
僕「え? いまどんな計算やった?」
ユーリ「え?」
僕「僕はこうやって解いたよ。数学を除いた $4$ 科目の平均点を $x$ 点とすると、 $4$ 科目の合計点は $4x$ 点。 それに $100$ 点の数学を加えて、 $5$ 科目の合計点は $4x + 100$ 点。 ところで、 $4$ 科目より $5$ 科目のほうが $5$ 点だけ平均点がアップしてるから、 $5$ 科目の平均点は $x + 5$ となる。 ということは $5$ 科目の合計点は $5(x + 5)$ ともいえる。こういう二つの見方で $5$ 科目の合計点を考えると、 $$ 4x + 100 = 5(x + 5) $$ という一次方程式が立てられる。 これを解くと $x = 75$ になる。 つまり、 $4$ 科目の平均点は $75$ 点で、 $5$ 科目の平均点は $80$ 点」
ユーリ「え、お兄ちゃんはこれ、暗算で解けるの?」
僕「まあ、このくらいは。 ちゃんと書いてもいいけど…… $$ \begin{align*} 4x + 100 &= 5(x + 5) && \textbf{上の一次方程式} \\ 4x + 100 &= 5x + 25 && \textbf{展開した} \\ 100 - 25 &= 5x - 4x && \textbf{移項した} \\ x &= 75 && \textbf{計算して右辺と左辺を交換した} \\ \end{align*} $$ ……結果は同じだね」
ユーリ「こーゆー感じでユーリは考えたよ。あのね、数学の $100$ 点から《$5$ 科目平均を超えた分》を、 《残りの $4$ 科目にわけてあげる》の。 そのためにはアップした $5$ 点が $4$ 科目分だから $20$ 点わけてあげることになるでしょ? だとしたら、 数学の点数から $20$ 点引いた分が $5$ 科目平均」
ユーリの考え
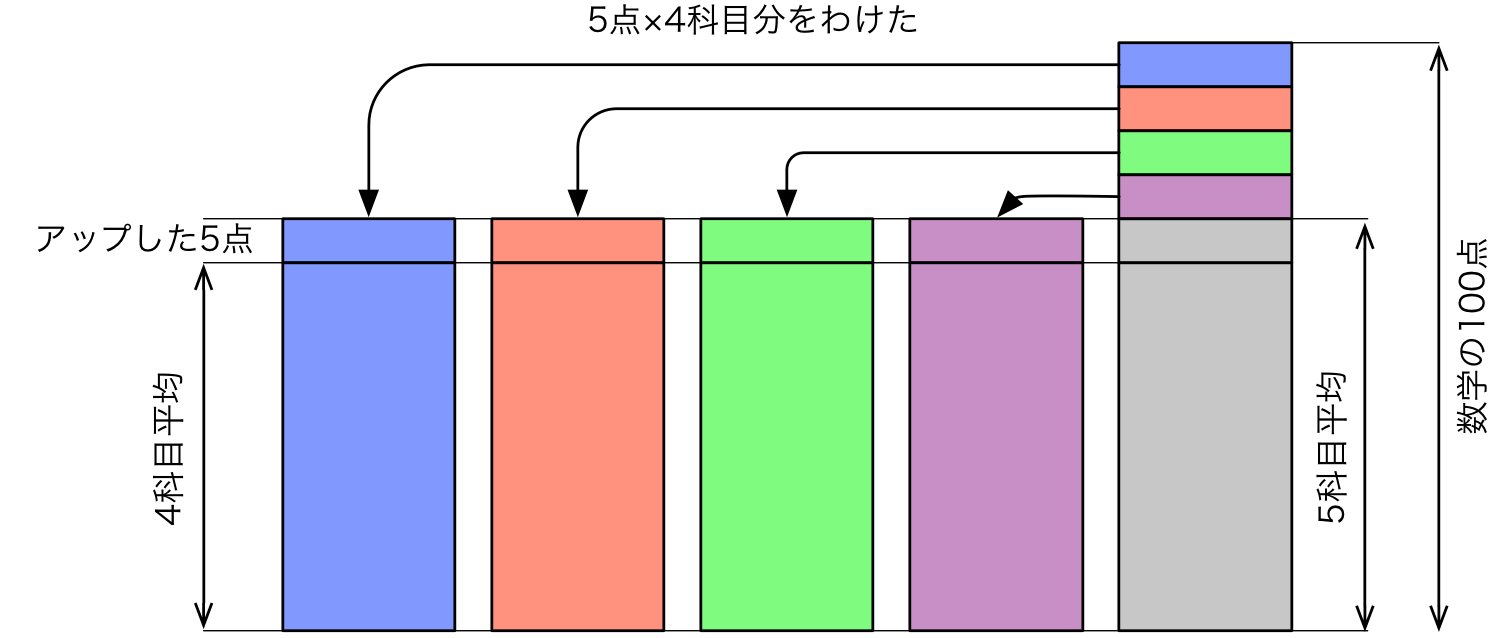
僕「ああ、なるほど。このほうがずっとわかりやすいな」
ユーリ「へっへー……じゃなくて! さりげなくテストの点数聞き出すなんて、 ちょっとひどくない? お兄ちゃんの(ピーーーー)!」
僕「ごめんごめん」
ユーリ「ぷんぷん」
僕「べつにそういうつもりで聞いたんじゃないんだけどな」
ユーリ「まー、いーけど。うっかり数学トリックに引っかかってしまったぜ!」
僕「べつにトリックで引っ掛けようと思ったわけじゃないよ……」
ユーリ「でも、このトリック、友達の点数聞き出すのに使えるね。メモメモ……」
$5$ 科目めのテストの点数を聞く($a$ とする)。
$4$ 科目の平均点から $5$ 科目の平均点がどれだけ上がったかを聞く($d$ とする)。
このとき、 $5$ 科目の平均点は、 $$ a - 4d $$ で求められる。
僕「そうだね。ユーリの場合は $a = 100, d = 5$ で、 $a - 4d = 80$ だったわけだ」
ユーリ「平均ってアナドれない……」
僕「平均値は代表値のひとつだから、いろんなことがわかっちゃうんだよ」
ユーリ「だいひょうち?」
僕「データとしてたくさんの数を扱いたい。 でも、あまり多すぎると扱いが難しくなる。だから《一つの数》で代表させたくなる。 たくさんの数をひとつひとつ知らなくても、その代表値さえわかっていたら、 データについてだいたいのことがわかる。そういう数を代表値っていうんだよ。平均値は代表値の一つだね」
ユーリ「ふーん」
僕「いまも、ユーリの点数が全科目バレたわけじゃないよね。 わかったのは数学の点数だけ。でも平均点が $80$ 点だってわかると、 全科目の点数がわからなくても、成績の様子はある程度わかる。 平均点が $80$ 点ということは $5$ 科目の合計点は $400$ 点で……」
ユーリ「具体的な数値はいーから。今回の期末は社会が足をひっぱったんだよー」
僕「今回の期末テスト、ユーリは数学で $100$ 点だった。 もちろんこれはユーリの $5$ 科目の点数というデータの中で最大値になるよね。 最大値も代表値の一つ」
ユーリ「あ、平均値だけじゃないんだ」
僕「そうだね。ほら、平均点が $80$ 点としても、 $5$ 科目の点数がどうなっているか、正確にはわからない。 $5$ 科目がすべて $80$ 点でも平均点は $80$ 点だし」
ユーリ「だから、具体的な点数はいいって!」
僕「最大値と同じように最小値も代表値の一つになる。 で、足をひっぱったという社会は何点?」
ユーリ「モクヒします。しつこいと嫌われるよ!」
僕「黙秘権を行使されてしまった。 じゃあ、ユーリの点数を追求するのはもうやめることにしようか」
ユーリ「当然じゃ。 ところで、最大値が代表値の一つって、何だかナットクできない」
僕「どうしてだろう」
ユーリ「だって、最大値って、データの中で一番大きな数ってことでしょ。 他にどんだけ小さな数があっても最大値は変わらないじゃん? それなのに代表値なの?」
僕「そうだよ。でもユーリが言いたいことはわかる。 ユーリが考えてるように、確かにデータの中にいくら小さい数があっても、最大値は変わらない。 二つのクラス、A組とB組で数学の点数を比べるとき、A組にもB組にも $100$ 点とった生徒がいたら、 どちらのクラスの点数も最大値は $100$ 点で同じになっちゃうね」
ユーリ「そーだよ。もしかしたらA組は $100$ 点の生徒が一人だけであとは全員 $0$ 点かもしんない。 B組は全員が $100$ 点かもしんない。それなのに両方とも最大値は $100$ 点じゃん!」
僕「それは『AとBでどちらの点数がクラス全体として良かったかを比較したいとき』には、 最大値を使うのはふさわしくないというだけだよ。 代表値にはいろんな種類があるから、 どんなときにどんな代表値を使うかを考えなくちゃいけない。 それから、データについて何か話している人がいたら、 『どんな代表値を使って話しているのか』を注意して聞かなきゃいけない」
ユーリ「ふむふむ? でも、最大値を使うときなんてあるの?」
僕「そりゃあるさ。 試験でもスポーツ大会も何でも《一番大きな値》は注目に値するよね。 あるランナーの過去の記録で一番大きな値は何か、というのはその選手の最高の力を表現するわけだから」
ユーリ「ははー、そりゃそーだね。 でもお兄ちゃん、ランナーの場合はタイムだから《最大値》じゃなくて《最小値》に注目するよね」
僕「うっ……ツッコミ容赦ないな」
ユーリ「平均値、最大値、最小値の三種類が代表値なの?」
僕「他にもあるよ。たとえば、最頻値」
ユーリ「さいひんち?」
僕「代表値として、平均値はよく使われるけれど、平均値では状況がよくわからない場合もある。 たとえば、さっきユーリが言ったみたいな極端な例を出すよ。 $10$ 人の生徒のうち $100$ 点が $1$ 人で残りの $9$ 人は $0$ 点だとする」
ユーリ「一人勝ちか……」
僕「このとき点数の平均値はいくらになる?」
ユーリ「全員の合計点は一人が稼いだ $100$ 点しかなくて、 人数は $10$ 人だから、 $100 \div 10 = 10$ で平均値は $10$ 点」
僕「そうだね。全員の合計点を人数で割って、平均値は $10$ 点。これは正しい計算だし、まちがっているところは何もない。 でも、何だか変な感じがする」
ユーリ「『平均値が $10$ 点』っていうと、 『だいたいの人が $10$ 点取ってる』みたいなイメージがする」
僕「うんうん、ついそう考えちゃう。でもこの場合はほぼ全員が $0$ 点を取ってる。 だから、『平均値が $10$ 点だから、だいたいの人が $10$ 点取ってる』とイメージしちゃうのは危険だね。 平均値の計算が数学的に正しくても、その平均値をどう解釈するかは十分気を付けなきゃいけない」
ユーリ「でも、 $10$ 人中 $9$ 人が $0$ 点だからといって、 『この場合は平均値を $0$ 点にしよう』なんていえないでしょ?」
僕「うん、それはいえない。勝手に平均値の定義を変えるわけにはいかないから」
ユーリ「あ、そっか。平均値を使うんじゃなくて、最小値を使えばいーのか。 『最小値は $0$ 点』は正しいでしょ?」
僕「それは正しい。 でも今度は、データを見たときに僕たちが感じる『$0$ 点を取ってる人が多い』という感覚はまったくなくなってしまったね」
ユーリ「まーね」
僕「だから、こういう場合のために別の代表値がある。それが最頻値だね。 最頻値の『頻』は、頻繁の『頻』。 さっきの例でいうと、 $100$ 点の人は $1$ 人で、 $0$ 点の人が $9$ 人だった。 人数がいちばん多い $9$ 人が $0$ 点をとった。この場合『最頻値は $0$ 点』になる」
ユーリ「にゃるほど。そっか! 『最頻値は $0$ 点』といえば、 『$0$ 点を取っている人がいちばん多い』ってことだね」
僕「そういうこと。 これで、代表値として、最大値、最小値、平均値、最頻値の話をした」
ユーリ「これで全部?」
僕「いやいや、代表値はもっとあるよ。 たとえば、 $10$ 人が $10$ 点満点のテストを受けて、こんな結果になったとしよう」
$$ \newcommand{\arraycolsep}{0pt} \begin{array}{|c|cccccccccc|} \hline \REMTEXT{点数} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \REMTEXT{人数} & 1 & 2 & 2 & 1 & 3 & 0 & 0 & 0 & 0 & 0 & 1 \\ \hline \end{array} $$ユーリ「ふんふん。最大値の $10$ 点が飛び抜けて輝いてるね」
僕「最大値は $10$ 点、最小値は $0$ 点、平均値は?」
ユーリ「えーと……点数×人数を全部足して、人数で割るんでしょ? $(2 + 4 + 3 + 12 + 10) \div 10 = 31 \div 10 = 3.1$ だから、 平均値は $3.1$ 点」
僕「それでいいね。平均値は $3.1$ 点。それから、最頻値は $4$ 点になる。人数が一番多いのは $4$ 点だから」
ユーリ「それで?」
僕「このデータを見てみると、一人だけ飛び抜けて点数が高い人がいる。 そして、この人が平均値を上げている」
ユーリ「でも、それはあたりまえでしょ?」
僕「そうだね。こういう飛び抜けた値のことを《はずれ値》っていうんだけど、 場合によってはそういう《はずれ値》の影響を受けない代表値がほしくなる場合もある。 それが中央値なんだ」
ユーリ「中央……まんなかの値?」
僕「そう。生徒を点数順にずらっと一列に並べる。 そして、その真ん中にいる生徒の点数が中央値になる。 言い換えると、その点数以上の生徒の人数と、その点数以下の生徒の人数が等しくなるような値が中央値なんだ」
ユーリ「んー……」
僕「何かおかしい?」
ユーリ「《例示は理解の試金石》ってお兄ちゃんがよくいうから、 さっきのデータで中央値を考えようと思ったんだけど……ここには $10$ 人いて、偶数だから、 まんなかの人いないじゃん!」
僕「ああ、偶数人のときには真ん中をはさむ二人の平均値を中央値にすることに決まってるんだよ」
ユーリ「なーんだ。だったら、このデータの中央値は上から $5$ 人目と下から $5$ 人目の平均値?」
僕「そうなるね」
ユーリ「上から $5$ 人目は $3$ 点で、下から $5$ 人目は $2$ 点だから、平均を取って $2.5$ 点。中央値は $2.5$ 点?」
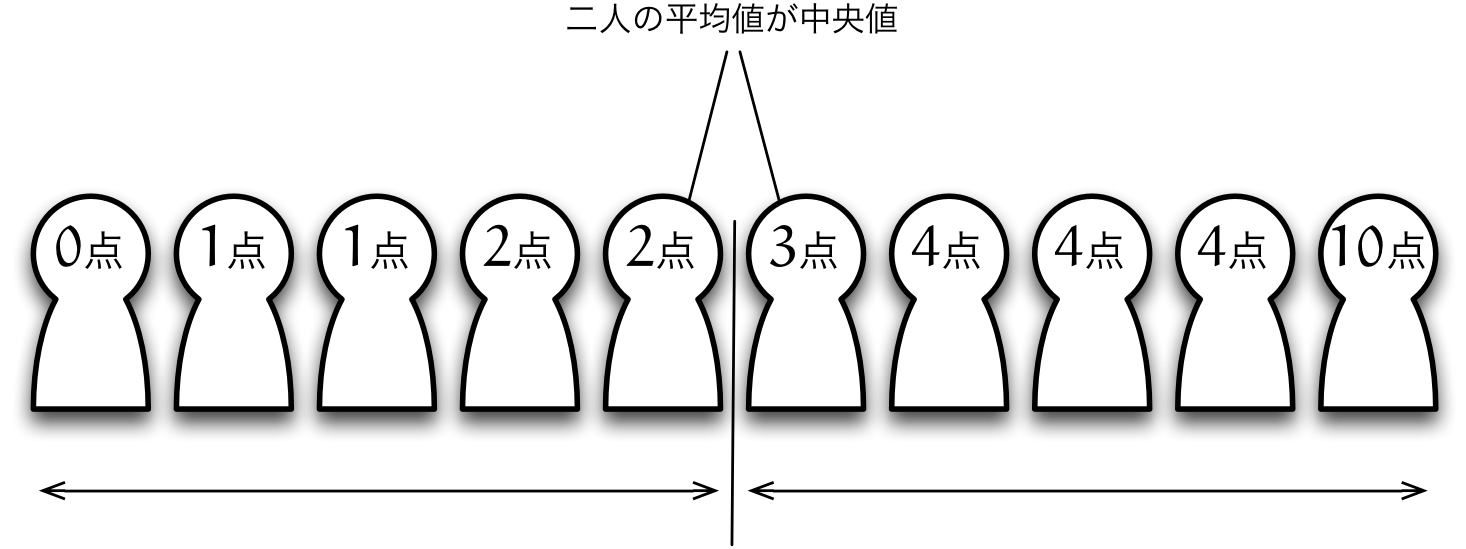
僕「はい、正解」
さまざまな代表値 $$ \newcommand{\arraycolsep}{0pt} \begin{array}{|c|cccccccccc|} \hline \REMTEXT{点数} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \REMTEXT{人数} & 1 & 2 & 2 & 1 & 3 & 0 & 0 & 0 & 0 & 0 & 1 \\ \hline \end{array} $$
ユーリ「ねーお兄ちゃん。これはこれでわかったんだけど、 こんなにたくさん代表値があったら、どれで考えればいいか、ごちゃごちゃすんじゃない?」
僕「あはは、そうだね。《代表値の代表値》がほしくなるかも」
ユーリ「平均値はわかる。平均はよく使うもん。 最大値と最小値もわかる。最頻値はいちばん多いところだからそれもわかる。 何だかよくわかんないのが中央値」
僕「え、そうかなあ。中央値はわかりやすいじゃないか。 だって点数の順番に並べて……」
ユーリ「それはそーなんだけど、平均値や最頻値で十分じゃないの?」
僕「そんなことはないよ。たとえばよくニュースでも出てくるけど、 年収や資産を考えるときには、中央値は大事な値になる」
ユーリ「へー」
僕「さっきもいったけど、中央値はデータの中に《はずれ値》があっても影響を受けない。 だから、ビル・ゲイツみたいな大富豪がいても影響を受けないんだよ」
ユーリ「あ、なるほど……でも、大富豪が大半だったら、中央値でも影響を受けるよね」
僕「そんな状況だったら、大富豪はもう《はずれ値》じゃないよ」
ユーリ「そっか」
僕「もちろん、代表値はたった一つの数でデータ全体のようすをつかもうとしているわけだから、 どうしても無理はある」
ユーリ「無理って?」
僕「つまり、一つの代表値でデータ全体がすべてわかるわけじゃないってこと」
ユーリ「そりゃそーだ。でも、グラフを描けばわかるんじゃないの? わざわざ一つの数にしなくても」
僕「確かにグラフは大事だね。 それでも、代表値をつかまえておくと便利なことが多い。 たとえば、毎年毎年変化していくデータというのはよくある。 そのときに、グラフの変化を調べることも大事だけれど、 毎年の代表値の変化を見ていくことも大事だね」
ユーリ「そかそか。たくさんの数をまとめて一つの数にしておけば、その変化を見ればいい?」
僕「それもまた、データを見る方法の一つということだね」
ユーリ「あれ? ……でも、わかんなくなってきた。グラフで平均値ってどこになるの?」
僕「え?」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第121回終わり)
(2015年7月3日)
この記事は『数学ガールの秘密ノート/やさしい統計』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!