![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだけれど飽きっぽい。
僕とユーリは、行列式の意味についてあれこれ話していた(第119回参照)。
僕「だから、行列式 $ad - bc$ は平行四辺形の面積になるんだね。 二つのベクトルの位置関係も考えて符号が付くことになるけど」
ユーリ「ふんふん。お兄ちゃんは式で計算したけど、 ユーリが考えた図形の方がわかりやすいよね」
僕「まあね。でも、ちゃんとすべての場合を尽くしているか、 図形だとわかりにくくなることもあるんだよ」
ユーリ「あー、それはそーかも」
ユーリ「ねー、正方形がひしゃげて平行四辺形になるなら、 どんどんつぶれていくよね」
僕「どんどんつぶれていく、とは?」
ユーリ「だから、いっかい変換したら正方形が平行四辺形になるじゃん? それで、もっかい変換したらもっとつぶれた平行四辺形になるよね?」
僕「ああ、それはそうだね。うんうん。同じ行列 $A$ で二回変換するってことになるから、二乗した行列 $A^2$ で一回変換したのと同じ」
行列 $A$ で一回変換
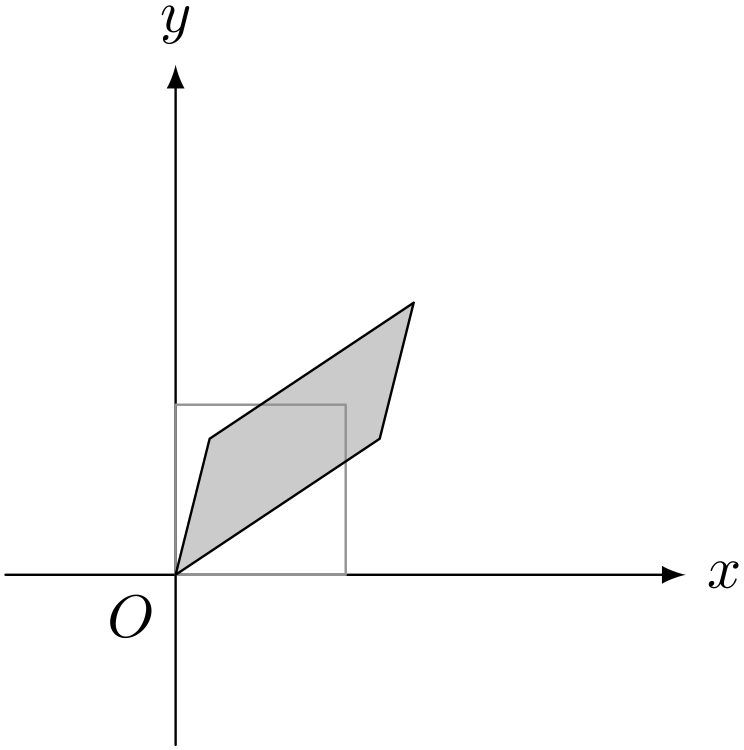
行列 $A$ で二回変換(行列 $A^2$ で一回変換)
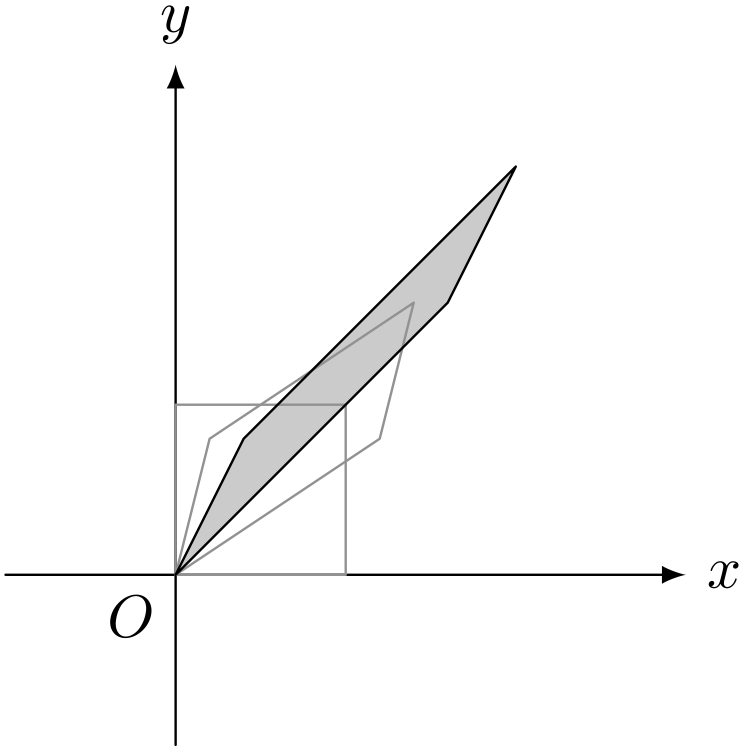
ユーリ「そー考えるんだ。じゃ、面積もわかるの?」
僕「面積もわかるのか、とは?」
ユーリ「ねー、お兄ちゃんって人の話聞いてる? 毎回聞き返さないでよー」
僕「聞いてるから聞き返せるんじゃないか。 お兄ちゃんがユーリに聞き返すのは、意味がわからないからだよ」
ユーリ「行列式が面積を表すなら、二回変換したときの面積も行列式でわかるんですか、お兄ちゃんセンセー……っていう意味!」
問題
$ad - bc > 0$ とする。
座標平面上の四点 $(0,0), (1,0), (1,1), (0,1)$ で作られる正方形を、 行列 $A = \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ で変換すると、平行四辺形に移る。 その平行四辺形の面積 $S$ は、
$$ S = ad - bc $$ で表される。 同じ正方形を行列 $A^2$ で移したときの平行四辺形の面積 $T$ を求めよ。

僕「なるほどね……これはおもしろい問題だよ」
ユーリ「上から目線はいーから」
僕「これはすぐにわかるよ。もとの正方形は面積が $1$ で、 それが行列 $A$ で移されたときには面積は $ad - bc$ になる。 座標平面上のどんな図形でも同じだけの比率で面積は変化してるから、 行列 $A$ で変換すると、面積は $ad - bc$ 倍になるわけだ。 面積が $ad - bc$ の平行四辺形をもう一度行列 $A$ で変換したら、 さらに $ad - bc$ 倍になるから、結局、求める面積 $T$ は $(ad - bc)^2$ になる」
解答
$A^2$ が移した平行四辺形の面積 $T$ は、 $$ T = (ad - bc)^2 $$ で表される。
ユーリ「そっか、それだけのことなんだ」
僕「そうだね。じゃ、ここで」
ユーリ「来たな《一般化》」
僕「おっと」
ユーリ「パターンじゃん。お兄ちゃん、一般化好きだから」
ユーリ「《変数の導入による一般化》でしょ? $3$ 回変換したら、 $4$ 回変換したら、 $5$ 回変換したら……それでは $n$ 回変換したら面積はどうなりますか?」
ユーリ「はーい」
ユーリ「かわいいユーリちゃん、お答えください」
ユーリ「$n$ 回変換したら、面積は $(ad - bc)^n$ になりまーす」
ユーリ「はいよくできました」
僕「一人芝居終わった?」
ユーリ「終わった」
僕「ユーリのいうとおり。行列 $A$ で $n$ 回変換するというのは、 行列 $A^n$ で変換するのと同じことで、面積はもとの図形の $(ad - bc)^n$ 倍になる」
ユーリ「ふふん」
僕「ではここで《一般化》してみよう」
ユーリ「は? いまやったじゃん」
僕「ユーリは、《行列 $A$ で $2$ 回変換する》を《行列 $A$ で $n$ 回変換する》にしたんだろ? $n$ という文字を導入して」
ユーリ「そだよん」
僕「一般化はいろんな方向にできるんだよ。 《行列 $A$ で $2$ 回変換する》を《行列 $A$ と行列 $B$ で変換する》という具合にね」
ユーリ「ほほー! 違う行列ってこと?」
僕「そうだね。《行列 $A$ で変換して、その後、行列 $B$ で変換する》というのは、 まとめると……」
ユーリ「行列 $AB$ で変換するってこと?」
僕「そうじゃなくて、行列 $BA$ だね」
ユーリ「あそっか。順番があるんだ」
僕「行列 $A$ の行列式も、行列 $B$ の行列式も $0$ より大きいとしよう。 面積が $1$ の正方形を行列 $BA$ で変換したら、どうなるかな?」
問題
$ad - bc > 0, ps - qr > 0$ とする。
座標平面上の四点 $(0,0), (1,0), (1,1), (0,1)$ で作られる正方形を、 行列 $A = \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ と $B = \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)$ の二つで変換すると、 平行四辺形に移る。 その平行四辺形の面積 $U$ を求めよ。
ユーリ「えっと……」
僕「……」
ユーリ「あれ? これ、簡単だよね?」
僕「まあ、そうだね」
ユーリ「両方の行列式の積?」
僕「そういうことになるね。 $A$ で変換して $ad - bc$ 倍になって、 $B$ で変換して $ps - qr$ 倍になる。 いいかえるなら、行列 $BA$ で変換した平行四辺形の面積は、 $(ps-qr)(ad - bc)$」
解答 $$ U = (ps - qr)(ad - bc) $$
ユーリ「ふむふむ」
僕「行列 $A$ の行列式を、絶対値の記号を借りて $|A|$ で表すことにすると、 $$ |BA| = |B||A| $$ が成り立つよ」
ユーリ「へ? ちょっと待って。ほんとに? ……あ、でもそーなるはずなのか!」
僕「何が?」
ユーリ「さっきのは平行四辺形の面積の話だったじゃん? 平行四辺形の面積が行列式で表されるのはわかったし、 二回変換する話もわかったけど、そっか、そーなるんだ! うわ不思議」
僕「だから、何が不思議?」
ユーリ「だってね、 $BA$ って行列の掛け算だから、 めんどくさい計算になるわけじゃん」
僕「ああ、まあね。成分で計算したらね」
ユーリ「$BA$ の行列式って、そのめんどくさい計算の後に、 さらに、行列式を計算するわけでしょ?」
僕「もちろん」
ユーリ「で、その結果は、 $ad - bc$ と $ps - qr$ の積になるの? そんなにうまくいくもんなの?」
僕「そういえば、実際に計算したことなかったけど、きっとうまくいくと思うよ。 こうだね」
問題
$A = \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ とし、 $B = \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)$ とする。
$$ |BA| = |B||A| $$ を成分計算を行って確かめよ。
ただし、 $|A|$ は行列 $A$ の行列式を表す。
ユーリ「ぐえ……言わなきゃよかった。計算ドリル」
僕「まずは $BA$ の成分計算から」
$$ \begin{align*} BA &= \left(\begin{array}{cc} p & q \\ r & s \end{array} \right)\left(\begin{array}{cc} a & b \\ c & d \end{array} \right) \\ &= \left(\begin{array}{cc} pa + qc & pb + qd \\ ra + sc & rb + sd \end{array} \right) \\ \end{align*} $$ユーリ「で、行列式でしょ?」
僕「そうそう」
$$ \begin{align*} & |BA| \\ &= (pa + qc)(rb + sd) - (pb + qd)(ra + sc) \\ &= parb + pasd + qcrb + qcsd - (pbra + pbsc + qdra + qdsc) \\ &= \UL{parb} + pasd + qcrb + \UL{\UL{qcsd}} - (\UL{pbra} + pbsc + qdra + \UL{\UL{qdsc}}) \\ &= pasd + qcrb - pbsc - qdra \\ \end{align*} $$ユーリ「あっ、消えた!」
僕「消えたねえ。こんどは $|B||A|$ のほうを計算しよう」
$$ \begin{align*} & |B||A| \\ &= (ps - qr)(ad - bc) \\ &= psad - psbc - qrad + qrbc \\ &= pasd + qcrb - pbsc - qdra \\ &= |BA| && \REMTEXT{上の計算から} \end{align*} $$ユーリ「おおっ! ほんとに等しくなった!」
僕「なったねえ……」
ユーリ「行列式ってよくわかんなかったけど、 平行四辺形の面積だと思うとちょっとわかる」
僕「そうだね。行列式が $0$ だと平行四辺形がつぶれてしまう。 逆変換もできなくなるし、逆行列も存在しない」
ユーリ「うんうん」
僕「行列式が $0$ だと逆行列が存在しないから、連立方程式も……」
ユーリ「連立方程式?」
僕「連立方程式はわかるよね、ユーリ。複数の方程式を並べて……」
ユーリ「連立方程式はわかるよー。連立方程式がなんで急にいま出てきたの?」
僕「だって、逆行列が存在するっていうのは、 連立方程式の解が唯一定まるということになるからだよ。あれ?」
ユーリ「あれ?」
僕「わかった。ちゃんと書くよ。こんなふうに、行列と縦ベクトルの積を考える」
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV x y $$ユーリ「はあ」
僕「こういう行列と縦ベクトルの積の結果は縦ベクトルになるよね」
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV x y = \VECV{ax+by}{cx+dy} $$ユーリ「そだね。行列の積の前半分だもんね」
僕「前半分って……まあ、そういえばそうだね。前半分というか、左半分というか。 ……それで、 $\left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV x y$ の結果が縦ベクトル $\VECV u v$ に等しくなったとする」
$$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV x y = \VECV u v $$ユーリ「ふんふん?」
僕「この《行列と縦ベクトルの積が、ある縦ベクトルの積に等しいということを表した式》は《連立方程式》と同じ形になっているよね」
《行列と縦ベクトルの積》と《連立方程式》 $$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)\VECV x y = \VECV u v $$
$$ \left\{\begin{array}{llll} ax + by &= u \\ cx + dy &= v \\ \end{array}\right. $$
ユーリ「えーと? あ、そーいえばそーなるね。 ねーお兄ちゃん。 $a,b,c,d$ と $u,v$ が数のつもりなんだもんね、この式」
僕「まあ $x,y$ も数のつもりだけど。 連立方程式の言い方をすると……《未知数》を $x,y$ として、 $a,b,c,d$ と $u,v$ が数として与えられていて、 それでこの連立方程式を解いて、 $x,y$ を求めようということ。 数で書いた方がわかりやすいかな」
《行列と縦ベクトルの積》は《連立方程式》と同じ形 $$ \left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)\VECV x y = \VECV 5 {16} $$
$$ \left\{\begin{array}{llll} x + y &= 5 \\ 2x + 4y &= 16 \\ \end{array}\right. $$
ユーリ「こんなの、すぐ解けるよ。えっとね。上 $2$ 倍して、引き算して…… うん、 $x = 2$ で $y = 3$ だね」
僕「いまユーリは連立方程式を解いたけど、 行列でも考えることができるよ。逆行列を使うんだ。 $\left(\begin{array}{cc} a & b \\ c & d \end{array} \right)$ の逆行列は、 $$ \left(\begin{array}{cc} a & b \\ c & d \end{array} \right)^{-1} = \frac{1}{ad - bc} \left(\begin{array}{cc} d & -b \\ -c & a \end{array} \right) $$ だったよね(第115回参照)(第116回参照)。 だから、 $\left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)$ の逆行列は、 $$ \begin{align*} \left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)^{-1} &= \frac{1}{1\times4 - 1\times2} \left(\begin{array}{cc} 4 & -1 \\ -2 & 1 \end{array} \right) \\ &= \frac{1}{2} \left(\begin{array}{cc} 4 & -1 \\ -2 & 1 \end{array} \right) \\ \end{align*} $$ となる」
ユーリ「逆行列を使う?」
僕「そうだね。さっきのこの式の左から、この逆行列 $\left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)^{-1}$ を掛けると、 $\left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)^{-1}\left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)$ は単位行列になる」
$$ \begin{align*} \left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)\VECV x y &= \VECV 5 {16} \\ \left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)^{-1}\left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)\VECV x y &= \left(\begin{array}{cc} 1 & 1 \\ 2 & 4 \end{array} \right)^{-1}\VECV 5 {16} \\ \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)\VECV x y &= \frac12\left(\begin{array}{cc} 4 & -1 \\ -2 & 1 \end{array} \right)\VECV 5{16} \\ \VECV x y &= \frac12 \VECV{4\times5 - 1 \times 16}{-2\times5 + 1\times 16} \\ &= \frac12 \VECV{4}{6} \\ &= \VECV 2 3 \\ \end{align*} $$ユーリ「……」
僕「ほら解けただろ? $\VECV x y = \VECV 2 3$ だから、 さっきユーリが連立方程式を解いて出した解の $x = 2, y = 3$ と同じになったね。 数字を文字に戻して一般的に書くなら……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年6月5日)
この記事は『数学ガールの秘密ノート/行列が描くもの』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!