第101回 シーズン11 エピソード1

冒険ビット（前編） ただいま無料

$2015$ を $2$ 進法で書く

ユーリ「あけおめー」

僕「おめー」

ユーリ「ことよろー」

僕「よろー」

ユーリ「ねー、お兄ちゃん知ってた？　 $2015$ って、 $2$ 進法で書くと左右対称なんだって」

僕「へえ、そうなんだ」

ユーリ「えーっとね、 $2015$ を $2$ 進法で書くと $11111011111$ なんだよー」

僕「ユーリ、そんなのよく気付いたなあ」

ユーリ「ネットで話題になってた」

僕「そうなんだ」

ユーリ「それからね、平成 $27$ 年の $27$ も $2$ 進法で書くと左右対称になるんだよ。 $11011$ だって！」

僕「おもしろいな……ユーリ、それメモしてたの？」

ユーリ「そーだよ。お兄ちゃんに教えてあげよーと思って」

僕「そりゃどうも」

ユーリ「こないだお兄ちゃんから $2$ 進法教えてもらってから、 ちょっと興味あるの」

僕「$2$ 進法の話なんてしたっけ？」

ユーリ「したじゃん。ほらほら《数当てマジック》のとき（『数学ガールの秘密ノート／整数で遊ぼう』参照）」

僕「なるほど。 $2$ 進法は好きだよ。 $2$ 進法がらみでは、いろんな数学者が出てくるけど、ライプニッツの話が特に好きだな」

ユーリ「誰それ」

僕「がく。ライプニッツは有名な数学者だよ。 ニュートンと並んで微分を考えた人でもある」

ユーリ「ふーん」

僕「ライプニッツはね、 $10$ 進法で数列を書くよりも $2$ 進法で書いた方が、 パターンを見つけやすくなるっていってる」

ユーリ「パターン？」

僕「うん。数列が持っているパターンが見つけやすくなるということは、 数列が持っている性質を見つけやすくなるってことだね」

ユーリ「そーなんだ」

僕「さっきユーリがいってた《左右対称》っていうのもパターンの一種といえるかも」

ユーリ「どーして、 $2$ 進法だとパターンが見つけやすいの？」

僕「どうして見つけやすいか……そうだなあ。 $2$ 進法で使われている数字は $0$ と $1$ しかないからかもね。 $10$ 進法だと $0$ から $9$ まで使うから、 数の並びがあったときにどれとどれが同じかわかりにくい。 でも $2$ 進法だと $0$ と $1$ だけだから、《$0$ が連続している》や 《いつも右端に $1$ が来る》や《左右対称》みたいな性質に気付きやすいのかな」

ユーリ「ふーん……」

$2$ 進法

ユーリ「ところで、 $2$ 進法って $0$ と $1$ しか使わないの？」

僕「えっ！　そうだよ。だって、 $2$ 進法だと、 $2$ になったら繰り上がりが起きるから」

ユーリ「あ、そっか」

僕「ほんとにわかってるのかなあ」

ユーリ「わーってるって」

僕「$0,1,2,3,4,5,\ldots$ を、 $2$ 進法で数えられる？」

ユーリ「えーと、たぶんね。最初 $0$ でしょ。次が $1$ で、そん次が $10$（イチゼロ）」

僕「そら、そこで繰り上がりが起きてるよね。 $1$ に $1$ 足したら、 $2$ 進法だと $10$ になる。繰り上がりして $2$ 桁の数になった」

ユーリ「そだね。ユーリ、表を作れるよ」

ユーリ「ね？　ちゃんとわかってるでしょ？」

僕「そうだね。ライプニッツの言う通り、 この表だけでもパターンがいくつか見えるよね」

ユーリ「縦読みするんでしょ？　一番右端の数は $0,1,0,1,0,1,\ldots$ になってる」

僕「うん。一番右端の数は、 $2$ 進法の《$1$ の位（くらい）》だね。 この数が $0$ ならば偶数だし、この数が $1$ ならば奇数だ」

ユーリ「それから、縦読みすると、右から二番目の数は $0,0$ と $1,1$ がかわりばんこ」

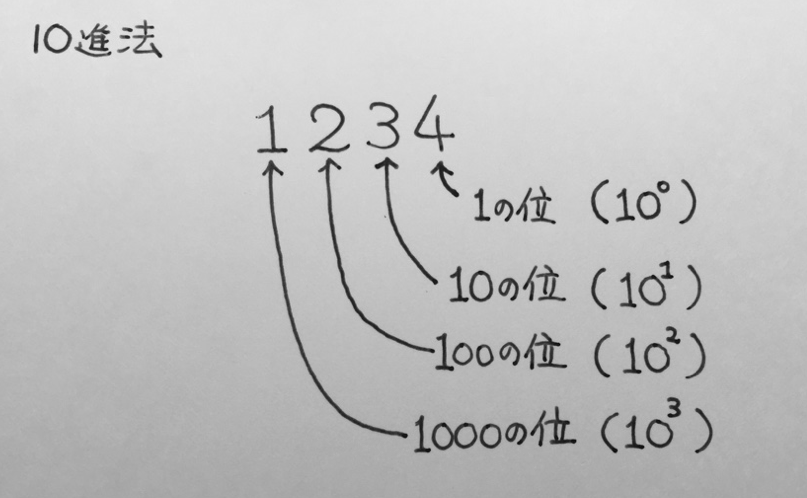
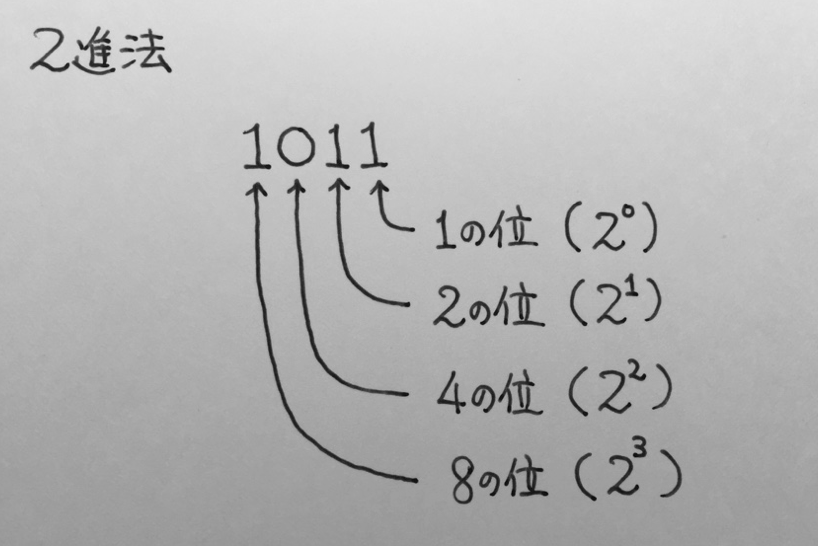
僕「右から二番目の数は、 $2$ 進法の《$2$ の位》になるね。 $10$ 進法だと《$1$ の位》《$10$ の位》《$100$ の位》《$1000$ の位》……になるけど、 $2$ 進法だと《$1$ の位》《$2$ の位》《$4$ の位》《$8$ の位》……になるんだよ」

ユーリ「ふんふん」

僕「じゃ、ここでクイズを出すよ」

ユーリ「なになに？」

僕「$10$ 進法で書いたときに $19$ になる数を、 $2$ 進法で書いたらどうなる？」

ユーリ「わかんない。覚えてないもん」

僕「がく。お兄ちゃんだって覚えていないよ。どうなるかを考えてほしいんだけど」

ユーリ「えー……あ、そっか。さっき $15$ までの表を作ったから、 そこから始めればいっか。 $15$ が $1111$ で、 $16$ が $10000$ で、 $17$ が $10001$ で、 $18$ が $10010$ だから、 $19$ は $10011$ だ！」

僕「はい正解。 $10$ 進法で $19$ と表す数は、 $2$ 進法では $10011$ と表せるね」

ユーリ「かんたんだよ」

僕「じゃ、 $39$ を $2$ 進法で書いたらどうなる？」

ユーリ「おんなじじゃん！　 $20$ のときは $10100$ ……みたいに書いてけばいーよね！　めんどいからやりたくないけど」

僕「うん、そういうと思ったよ。ユーリがさっきやったみたいに、 $1$ ずつ増やしていく方法は悪くない。でも、大きな数を $2$ 進法で表そうとしたときには、 すごくめんどうなことになってしまうよね」

ユーリ「そだね……でも、他に方法あるの？」

僕「それが問題になる」

ユーリ「どーすんのかにゃあ……」

僕「たとえば、こんなやりかたがある。 $10$ 進法で書かれた数を読むときに $1,10,100,1000,10000,\ldots$ と唱えるよね」

ユーリ「うん、やるやる。いち、じゅう、ひゃく、せん、まん」

僕「$2$ 進法でもそれと同じようにやってみる。 ただし、 $1,2,4,8,16,32,\ldots$ と唱える」

ユーリ「$2$ 進法だから $2$ 倍に？」

僕「そうだね。いま調べたいのは $39$ の書き方だから、 $39$ に近くなるまではその方法を使う。 $\underbrace{1,2,4,8,16,32}_{\REMTEXT{$6$個}}$だから、$2$進法で$100000$という$6$桁の数は$32$になる。 あとはこれに $10$ 進法の $7$ 、つまり $2$ 進法の $111$ を足せばいい。 $2$ 進法で $100000 + 111$ を計算すれば $100111$ だね。これが $39$ に相当する」

ユーリ「$7$ ってどっから来たの？」

僕「すでにわかった $32$ から、いま表したい数 $39$ まで進むのにあと $7$ ってこと。 つまり $39 - 32 = 7$ だね」

ユーリ「あ、そっか、わかった」

僕「いまのは、自分が $2$ 進法で表したい数の近くまでは、 倍々で進んでいくという方法だね。これだと $1$ ずつ増やすよりずっと楽だ」

ユーリ「でもさー、もっと大きな数だとやっぱりめんどくなるよ」

僕「うん、そろそろ一般的に《$10$ 進数を $2$ 進数で表す方法》を考えた方がよさそうだ。 そもそも、 $10$ 進法で $39$ になる数が、 $2$ 進法で $100111$ と書けるというのは、 どういうことかを考えてみよう。これは、こういうことなんだ」

ユーリ「？」

僕「つまり、 $39$ という数を、 $1,2,4,8,16,32,\ldots$ という $2$ の冪乗（べきじょう）の数の《和》の形で 表しているということ」

ユーリ「あー、そーだった。そんな話してたねー」

僕「$39$ という数は、 $32, 4, 2, 1$ という $2$ の冪乗の和に書ける。 これはそれぞれ $2^5, 2^2, 2^1, 2^0$ という形。 途中の $2^4$ と $2^3$ は飛ばしている。これを入れちゃうと $39$ は作れないから。 どの数を使って、どの数を飛ばすかは、 $1$ を掛けるか $0$ を掛けるかで表す。 $2$ 進法では $2$ の冪乗を使うことになっているから、 あとは、その $1$ と $0$ の並びさえわかればいいってことになる。 このときの $1$ と $0$ の並びが《$2$ 進法で書かれた数》すなわち《$2$ 進数》になる」

ユーリ「ふんふん」

僕「この《$2$ の冪乗のうち、どれを足してどれを足さないか》を表したものが $2$ 進数だとわかっていれば、 $10$ 進数を $2$ 進数に変換する方法も見つけることができるんだよ」

ユーリ「へー！」

僕「ひとことでいえば《繰り返して $2$ で割って余りを調べていく》というやり方なんだ」

ユーリ「どゆこと？」

僕「$39$ の例でいおう。 $39$ を $2$ で割ったときの余りは？」

ユーリ「$39 \div 2$ は $19$ で余りは $1$」

僕「そうだね。そしてこの余り $1$ は、 $39$ を $2$ 進法で表したときの一番右に来る数になる。《$1$ の位》」

ユーリ「なんで？」

僕「なぜだと思う？」

ユーリ「……あ！　そりゃそーじゃん。 $2$ 進数だと、偶数は $0$ で終わるし、奇数は $1$ で終わるもん。 $2$ で割って余り $1$ っていうのは要するに奇数ってことだし」

僕「そうだね。さっきの数式を思い出してもわかる。《$1$ の位》はちょうど $2$ で割った余りに相当する」

ユーリ「ほほー。そっか $2^0$ のところがちょうど余りになるんだ」

僕「これで、《$1$ の位》はわかったね。 そして、いま《$2$ でくくった》と書いたところをよく見ると、 ここも同じように考えればいいってことがわかる。 つまり、さっき《$39$ を $2$ で割ったときの商 $19$》を、 さらに $2$ で割って余りを求めるということ。これで《$2$ の位》がわかる」

ユーリ「ははーん、さっきお兄ちゃんが言った 《繰り返して $2$ で割って余りを調べていく》ってそーゆーこと？」

僕「実際に $39$ でやってみよう。こんなふうになる」

僕「これで、余りのところを順番に見ていくと $1,1,1,0,0,1$ だね。 これは下の位から見ていることになるから、逆転させて $100111$ になる。 $39$ を $2$ 進法で書くと、 $100111$ になるということだね」

ユーリ「あれ？　これやったことある。 ほら、お兄ちゃんが描いてくれた変なワニが出てきたやつ！」

僕「そうそう、そうだったね。 この方法を使えば、自分の手で $2015$ を $2$ 進法で書いたらどうなるかを調べられるよ」

$2$ 進数をシグマで表す

僕「いまは $39$ を例に使って $2$ 進数の話をしたけど、 シグマ $\sum$ を使えば、もっと一般的に書くことができるよ」

ユーリ「キター！　お兄ちゃん得意の《一般的に書く》だ！」

僕「何興奮してんの」

ユーリ「お兄ちゃん、一般化するの好きだよね」

僕「まあね。さっきの $39$ の式をじっと見れば、一般的にどう書けばいいかはすぐわかるよ」

ユーリ「じー」

僕「まずは、 $0$ と $1$ の部分を $a_k$ という文字を使って書いてみよう。 $a_k$ という文字は、《$2^k$ の位》の数字が何になるかを表しているもの、ということに決めて」

ユーリ「ほほー……ねー、この $a_5$ とか、 $a_4$ って、 $0$ か $1$ かのどっちかだよね？」

僕「そうそう。それでと。いまは $6$ 桁の $2$ 進数固定になっているから、 $n$ 桁の $2$ 進数に変えてみよう。 途中にテンテン（$\cdots$）を入れる」

ユーリ「何で $n-1$ なの？　……わかった！　 $0$ から始めたからだね！」

僕「そうだね。《$n$ 桁の $2$ 進数》だとしたら、最上位は《$2^{n-1}$ の位》になる。 こういうのはすごくまちがいやすいところだね」

ユーリ「ねー、《$n+1$ 桁の $2$ 進数》を表すってことにすれば $a_n$ から $a_0$ まででちょーどいーんじゃないの？」

僕「うん、そういう表し方をしてもいいよ。それから、《$2^k$ の位》の数字を $a_{k+1}$ にするというやり方もある。 これは約束ごとなんだから、書く人が自由に決めていい。何を表しているかをはっきり言えば」

ユーリ「約束ごと……ね」

僕「さて、こんなふうにテンテンを使った足し算の形にうまく書けたら、シグマまではもう一息。 何しろシグマは足し算なんだから」

ユーリ「うわ、すごくややこし……くもないか」

僕「足し算を置き換えているだけだから、ぜんぜん、ややこしくないよね。 これで、 $2$ 進法で表した $0$ 以上の整数を、シグマで表現することができた」

左右対称の $2$ 進数

僕「これで、 $2$ 進数を数式で書くことができたね」

ユーリ「お兄ちゃんってほんとに、数式好きなんだね」

僕「そうだね。 そうだ！　ユーリがいってた《左右対称な $2$ 進数》もやってみようよ」

ユーリ「何をやるの？」

僕「数式……シグマを使って表してみるんだよ」

ユーリ「どゆ意味？」

僕「さっきは $\SUM_{k=0}^{n-1} a_k2^k$ という数式で、 $2$ 進数を書くことができたよね」

ユーリ「うん」

僕「どんな $2$ 進数でもこの数式で表現できる。 けれど今度は、左右対称な $2$ 進数に限って表現するような数式を作ろうということ」

ユーリ「左右対称……って、そんなこと数式で書けんの？」

僕「もちろん書けるよ。つまりこれは《言い換え》なんだ」

ユーリ「言い換え？」

僕「そう。さっき、 $2$ 進数はパターンが見やすいという話をしたよね。 $111101111$ や $11011011$ のように数字が並んでいると、パッと見て《あ、左右対称だ》ってわかる」

ユーリ「うん」

僕「それは見て分かるということ。 ではそれを数学の言葉……数式で表現し直してみよう。言い換えてみよう」

ユーリ「ふんふん。左右対称……さっぱりわかんない」

僕「じゃね、まずは数式じゃなくてもいいから自分の言葉で表現してみよう。 $11011011$ のような $2$ 進数は左右対称だよね」

ユーリ「そだね」

僕「なぜ、左右対称っていえるんだろう」

ユーリ「だって、左端から $1,1,0,1$ と並んでいて、右端からも同じく $1,1,0,1$ って並んでるから」

僕「そうだね！　一つずついこう。 《左端が $1$ で右端も $1$》つまり《左端と右端が等しい》」

ユーリ「$2$ 番目もそうだよ。左から $2$ 番目と右から $2$ 番目も等しい」

僕「$1$ 番目、 $2$ 番目、 $3$ 番目……ずっとそうだね。それが《左右対称》ということ」

ユーリ「あたりまえじゃん」

僕「ところで、僕たちはこんなふうにして $2$ 進数を数式で表現できる」

$$ {a_{n-1}}\cdot2^{n-1} + {a_{n-2}}\cdot2^{n-2} + {a_{n-3}}\cdot2^{n-3} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 $$

ユーリ「さっきやった」

僕「これで、左端の数字ってなんだろう」

ユーリ「えーっと、 $a_{n-1}$ かにゃ？」

僕「そう。じゃ、右端は？」

ユーリ「$a_0$ でしょ？」

僕「そうだね。ところで、左端の数字と右端の数字が等しいということは」

ユーリ「あっ！　 $a_{n-1} = a_0$ だ！」

僕「そうなるね。いいぞ！」

ユーリ「でも、こんなイコールをシグマに入れるの？」

僕「ちがうちがう。 $a_{n-1} = a_0$ ということは、 $a_{n-1}$ の代わりに $a_0$ を入れてもいいってことだよね。 だから、両端が等しい数字になった $2$ 進数っていうのはこんな形ってことだよね」

$$ {a_0}\cdot2^{n-1} + \cdots + {a_0}\cdot2^0 $$

ユーリ「あ、わかった。もー、いわなくっていい！同じこと繰り返せばいいんだね！　 こーだ！」

$$ {a_0}\cdot2^{n-1} + {a_1}\cdot2^{n-2} + {a_2}\cdot2^{n-3} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 $$

僕「そうだね！　これでほとんど正解なんだけど、一点注意が必要になる」

ユーリ「真ん中でしょ？　そかそか、 $n$ 桁のちょうど半分まで行くから、 $\frac{n}{2}$ まで……から $1$ 個ずれるから、うわめんどい」

$$ \begin{align*} & {a_0}\cdot2^{n-1} + {a_1}\cdot2^{n-2} + {a_2}\cdot2^{n-3} + \cdots + a_{\frac{n}{2}}\cdot2^{n - \frac{n}{2}} \\ & \quad + a_{\frac{n}{2}}\cdot2^{\frac{n}{2} - 1} + \cdots + {a_2}\cdot2^2 + {a_1}\cdot2^1 + {a_0}\cdot2^0 \\ \end{align*} $$

僕「うん、これでほとんど正解。ただしこれは、 $n$ が偶数の場合だよね。 $11$（$2$ 桁）や $1001$（$4$ 桁）や、 $110011$（$6$ 桁）のように、 偶数桁の場合は左右対称で《真ん中》に相当する数がない」

ユーリ「そっか、奇数の場合も考えると……？」

僕「《場合分け》になるね」

ユーリ「うわ……できたけど、すごくめんどい……」

僕「うーん、分数に持ち込んだのが敗因かな」

ユーリ「どゆこと？」

僕「ほら、《$n$ 桁の $2$ 進数》を表現しようとしたから、 $\frac{n}{2}$ や $\frac{n-1}{2}$ というのが出てきちゃったんだ」

ユーリ「だって、しょーがないじゃん」

僕「偶数桁は《$2m$ 桁の $2$ 進数》にして、奇数桁は《$2m+1$ 桁の $2$ 進数》にすれば、 もっとずっとすっきり書ける！」

ユーリ「あ、分数なくなった」

僕「そうだね。この方がずっとすっきりした」

ユーリ「あ！　お兄ちゃん、これおかしーよ！」

僕「何が？」

ユーリ「これだとね、たとえば、 $110$ も左右対称になってしまうもん！」

僕「何で？　ああっ、そうか。最上位の $0$ か……」

ユーリ「まー、でも $110$ を $0110$ だと思えば、左右対称になってるけど」

僕「うーむ……」

ユーリ「ねーお兄ちゃん」

僕「なに？」

ユーリ「ややこしいよーな、おもしろいよーな、変な感じ」

僕「そう？」

ユーリ「うん。あのね、数式はやっぱり、ややこしいんだけど、 何度も書いているうちに、何だか少し見慣れてきたのかなー。 それから分数がなくなったときは、おーっと思ったし」

僕「うんうん」

ユーリ「でもね、たとえば、この式 $\SUM_{k=0}^{m - 1} a_{k}\left(2^{2m-k} + 2^k\right) + a_{m}2^{m}$ みても《左右対称》って感じがしないの。だから変な感じ」

僕「なるほどね……非対称に見えるのは、 $2^{2m-k} + 2^k$ の部分だけだよね。 本来なら $s = 2m-k, t = k$ と置いて $2^s + 2^t$ のようにするといいんだけどね。 $0 \leqq t < m, s + t = 2m$ の条件を満たす整数 $s,t$ の範囲で和を取ることになる」

ユーリ「ふーん……ところで、 $2$ 進数じゃなくて $1$ 進数ってないの？」

僕「$1$ 進数？」

$1$ 進数

僕「いや、 $1$ 進数というのは……どうかな。だって繰り上がりできないし」

ユーリ「あのね、こーゆーの。 $1,11,111,1111,11111,\ldots$」

僕「ほう？」

ユーリ「その数の分だけ $1$ を並べちゃうの！　これって $1$ 進法っぽくない？」

僕「確かに、$n$を表すのに$\underbrace{111\cdots111}_{\REMTEXT{$n$個}}$という 書き方をすることにすれば、数は表しているな。でも『$1$ 進法』 と呼ぶのは苦しいなあ」

ユーリ「えー、そっかなー。なんで？」

僕「ほら、 $10$ 進法だと、 $10$ を表す数字はないよね。 $0,1,2,3,4,5,6,7,8,9$ の $10$ 種類の数字を使って一つの桁を表している」

ユーリ「うん」

僕「同じように、 $2$ 進法では、 $2$ を表す数字はなくて、 $0,1$ という $2$ 種類の数字を使って一つの桁を表す。 だから、もしも $1$ 進法があるとしたら、 $1$ を表す数字は使えない」

ユーリ「そっか……あっ！　だったら $0$ を並べればいいっ！……ちょっと無理があるか」

僕「そうだね。でも、そんなふうに概念を拡張して考えるのは楽しいよね」

$-2$ 進法？

ユーリ「$0$ 進法もダメだし……そうだ！　《$-2$ 進法》は？　ねーお兄ちゃん！　 これならできるじゃん？」

僕「マイナス $2$ 進法……えっと、ん？　できるのか？」

ユーリ「お兄ちゃんならできるよ、きっと！　問題にしちゃえ！」

僕「$-2$ 進法って何だろう。 $-2$ になるごとに繰り上がり？」

ユーリ「わけがわかんないね」

僕「いや、ちがうな。そこが本質じゃないんだ」

ユーリ「どこが本質？」

僕「$10$ 進法は、各桁の数字に $10$ の冪乗を掛けて表した。 $1,10,100,1000,10000,\ldots$ という具合に」

ユーリ「ふんふん？」

僕「同じように $2$ 進法は、 $2$ の冪乗を使った。 $1,2,4,8,16,32,\ldots$ だった。これは $2^0,2^1,2^2,2^3,2^4,2^5,\ldots$」

ユーリ「そーだったね。あ！」

僕「そうだ。もしも $-2$ 進法があるとしたら、 《$-2$ の冪乗》を使うんじゃないか？ つまり、 $(-2)^0,(-2)^1,(-2)^2,(-2)^3,(-2)^4,(-2)^5,\ldots$ を使う」

ユーリ「おー！　……でも、使う数字は？」

僕「よくわからないけど、 $0$ と $1$ でやってみよう。 うわ！」

ユーリ「どしたの？」

僕「そうか。 $-2$ の冪乗を使うってことは、正と負が入り交じる！」

ユーリ「へ？」

ユーリ「うっわ！　 $0,1,-2,-1,4,5,2,3$ なんて、順番ぐちゃぐちゃ」

僕「いや、わかったぞ。 $0,1$ のあと、 $2$ を作るためには $4-2$ だと考えればいいんだ。 つまり、軽いジャンプがあるんだよ。 《$(-2)^k$ の位》の数字を $a_k$ としたとき、 この一般式をじっと見て考えればわかる」

ユーリ「この式見てわかんの……？」

僕「少し頭をひねらないと難しいかな……いや、できるできる！」

ユーリ「あれ……お兄ちゃん！　パターンが見える！　ほらほら、縦読みすれば！」

僕「ほんとだ！」