第98回シーズン10 エピソード8

フラクショナル・フラクション（後編）

$ \newcommand{\SQRT}[1]{\sqrt{\mathstrut #1}} \newcommand{\GEQ}{\geqq} \newcommand{\LEQ}{\leqq} \newcommand{\NEQ}{\neq} \newcommand{\ABS}[1]{|#1|} \newcommand{\SQUX}{\textrm{square}} \newcommand{\EXPX}{\textrm{exp}} \newcommand{\LOGX}{\textrm{log}} \newcommand{\AVEX}{\textrm{average}} \newcommand{\TEXT}[1]{\textbf{#1}} \newcommand{\REMTEXT}[1]{\textbf{#1}} $

図書室にて

ここは僕の高校。いまは放課後。

僕、テトラちゃん、ミルカさんの三人で、村木先生からの問題を三問とも解いたところ。

すると、ミルカさんさんは三枚のカードの《共通テーマ》がわかったと言い出した。

ミルカ「わかったよ。三枚のカードに共通したテーマが」

僕「何？」

テトラ「何ですか？」

ミルカ「テトラの言葉がヒントになった」

テトラ「あ、あたし……なんて言ったでしょう」

ミルカ「《三枚のカードにはそれぞれに分数が出てきた》と言った」

僕「そうだったね」

ミルカ「三枚のカードを解いて出てきた大小関係を見る」

テトラちゃんのカード

$a,b$ が実数のとき、以下が成り立つ。等号成立は $a = b$ のとき。 $$ \dfrac{a^2 + b^2}{2} \GEQ \left(\dfrac{a + b}{2}\right)^2 $$

「僕」のカード

$s,t$ が実数のとき、以下が成り立つ。等号成立は $s = t$ のとき。 $$ \dfrac{e^s + e^t}{2} \GEQ e^{\frac{s + t}{2}} $$

ミルカさんのカード

$a > 0, b > 0$ のとき、以下が成り立つ。等号成立は $a = b$ のとき。 $$ \log \dfrac{a + b}{2} \GEQ \dfrac{\log a + \log b}{2} $$

僕「確かに分数は出てくるし、ぜんぶ二つの数が絡んでいるから雰囲気は似ているけど……」

ミルカ「伝統的な数式から発想を変えて考える」

テトラ「？」

ミルカ「この三枚のカードに出てくる演算を列挙すると、この四種類」

$$ \begin{array}{|c|c|} \hline \REMTEXT{$2$乗する} & \heartsuit^2 \\ \hline \REMTEXT{指数関数の値を得る} & e^\heartsuit \\ \hline \REMTEXT{自然対数を取る} & \log \heartsuit \\ \hline \REMTEXT{$2$数の平均を取る} & \dfrac{\heartsuit + \spadesuit}{2} \\ \hline \end{array} $$

僕「ふむふむ、確かに。この四種類を組み合わせているなあ」

ミルカ「数式では、演算によって書き方がばらばらだ。指数を右上に小さく書いたり、 $\log$ のように文字列を使ったり、分数の形にしたり」

テトラ「あ！　そのこと、あたしもよく気になります。いろんな書き方をしますよね。上に行ったり下に行ったり」

テトラちゃんはそう言いながら両手をぱたぱた振る。

ミルカ「不等式の類似点を探すため、 書き方を統一する」

$$ \begin{array}{|c|c|} \hline \REMTEXT{$2$乗する} & \SQUX(\heartsuit) \\ \hline \REMTEXT{指数関数の値を得る} & \EXPX(\heartsuit) \\ \hline \REMTEXT{自然対数を取る} & \LOGX(\heartsuit) \\ \hline \REMTEXT{$2$数の平均を取る} & \AVEX(\heartsuit,\spadesuit) \\ \hline \end{array} $$

僕「おっと、これは……なるほど」

テトラ「おもしろいです！　 $\SQUX$ は《平方》で、 $\AVEX$ は《平均》ですね」

ミルカ「言い換えると、こんなふうに関数を定義すると思えばいい」

関数を定義する

$$ \left\{\begin{array}{llll} \SQUX(x) &= x^2 \\ \EXPX(x) &= e^x \\ \LOGX(x) &= \log x \\ \AVEX(x,y) &= \dfrac{x+y}{2} \\ \end{array}\right. $$

テトラ「いままでバラバラだったものが、何だか《揃う》感じがします」

ミルカ「これらの関数を使って、もう一度、三枚のカードに出てきた大小関係を書き直す」

僕「なるほど！」

ミルカ「たとえば、テトラのカードに出てきた式を書き換えるとこうなる」

$$ \begin{align*} \dfrac{a^2 + b^2}{2} & \GEQ \left(\dfrac{a + b}{2}\right)^2 \\ & \REMTEXT{↓} \\ \AVEX(\SQUX(a), \SQUX(b)) & \GEQ \SQUX(\AVEX(a,b)) \\ \end{align*} $$

僕「確かにそうなるね……」

テトラ「これはあれですね？　 $a^2$ は $\SQUX(a)$ に置き換えて、 $b^2$ は $\SQUX(b)$ に置き換えて、さらにこの平均は $\AVEX(\SQUX(a),\SQUX(b))$ に置き換えて……というのを繰り返したのですね」

ミルカ「そう。三枚のカードはこうなる」

テトラちゃんのカード

$a,b$ が実数のとき、以下が成り立つ。等号成立は $a = b$ のとき。 $$ \AVEX(\SQUX(a), \SQUX(b)) \GEQ \SQUX(\AVEX(a,b)) $$

「僕」のカード

$s,t$ が実数のとき、以下が成り立つ。等号成立は $s = t$ のとき。 $$ \AVEX(\EXPX(s),\EXPX(t)) \GEQ \EXPX(\AVEX(s,t)) $$

ミルカさんのカード

$a > 0, b > 0$ のとき、以下が成り立つ。等号成立は $a = b$ のとき。 $$ \LOGX(\AVEX(a,b)) \GEQ \AVEX(\LOGX(a),\LOGX(b)) $$

テトラ「これは……見えてきましたようっ！　条件を省略して並べるともっとはっきりします！」

$$ \begin{align*} \AVEX(\SQUX(a),\SQUX(b)) & \GEQ \SQUX(\AVEX(a,b)) \\ \AVEX(\EXPX(s),\EXPX(t)) & \GEQ \EXPX(\AVEX(s,t)) \\ \LOGX(\AVEX(a,b)) & \GEQ \AVEX(\LOGX(a),\LOGX(b)) \\ \end{align*} $$

ミルカ「テトラはこの三式の共通点をどう表現する？」

テトラ「ええっとですね……何だかこう、inside out になっているような。《裏返し》という感じがします。 $\AVEX(\SQUX(a),\SQUX(b))$ では内側にあった $\SQUX$ が、 $\SQUX(\AVEX(a,b))$ では外側になってますから！」

僕「テトラちゃん、これが裏返しに見えるのは、関数表記だからだよ。これは《演算の順序交換》で大きさがどう変わるかという問題じゃないかな？」

テトラ「順序……交換？」

ミルカ「そういえる。演算の順序交換での大小変化」

テトラ「順序というのは、たとえば $\SQUX$ と $\AVEX$ のどちらを先にするかという意味でしょうか」

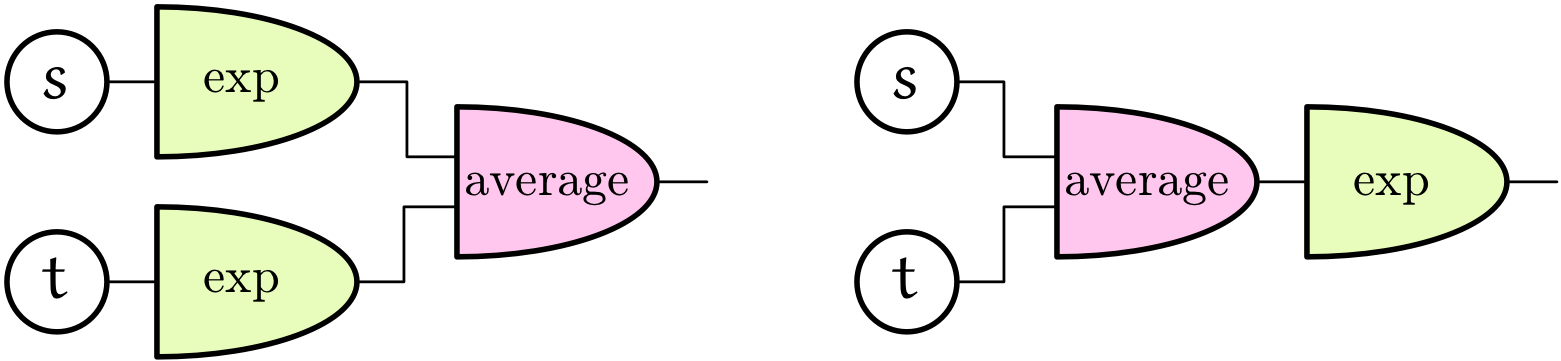
ミルカ「そう。関数表記をさらに変えて、電子回路風に描いてみると、順序の意味がよくわかるだろう」

$$ \AVEX(\SQUX(a),\SQUX(b)) \quad\REMTEXT{と}\quad \SQUX(\AVEX(a,b)) $$