![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
いまは放課後。 いつものように数学をしようと僕が図書室に入ると、 テトラちゃんとミルカさんが並んで書き物をしていた。 書き物というか……問題に挑戦しているようだ。
僕「テトラちゃん、問題?」
テトラ「あっ! 先輩っ! ちょっとお待ちくださいっ! ただいまバトル中っ!」
僕「バトルって……」
ミルカ「カード」
カードバトル……なわけはないな。
見ると、机の上には村木先生からのカードが置いてあった。 数学の問題だ。
村木先生からのカード
$n$ と $r$ を $1$ 以上の整数とし、 集合 $\SS{1,2,3,\ldots,n}$ を $r$ 個の空ではない部分集合に分割しよう。
たとえば、 $n = 4, r = 3$ のとき、
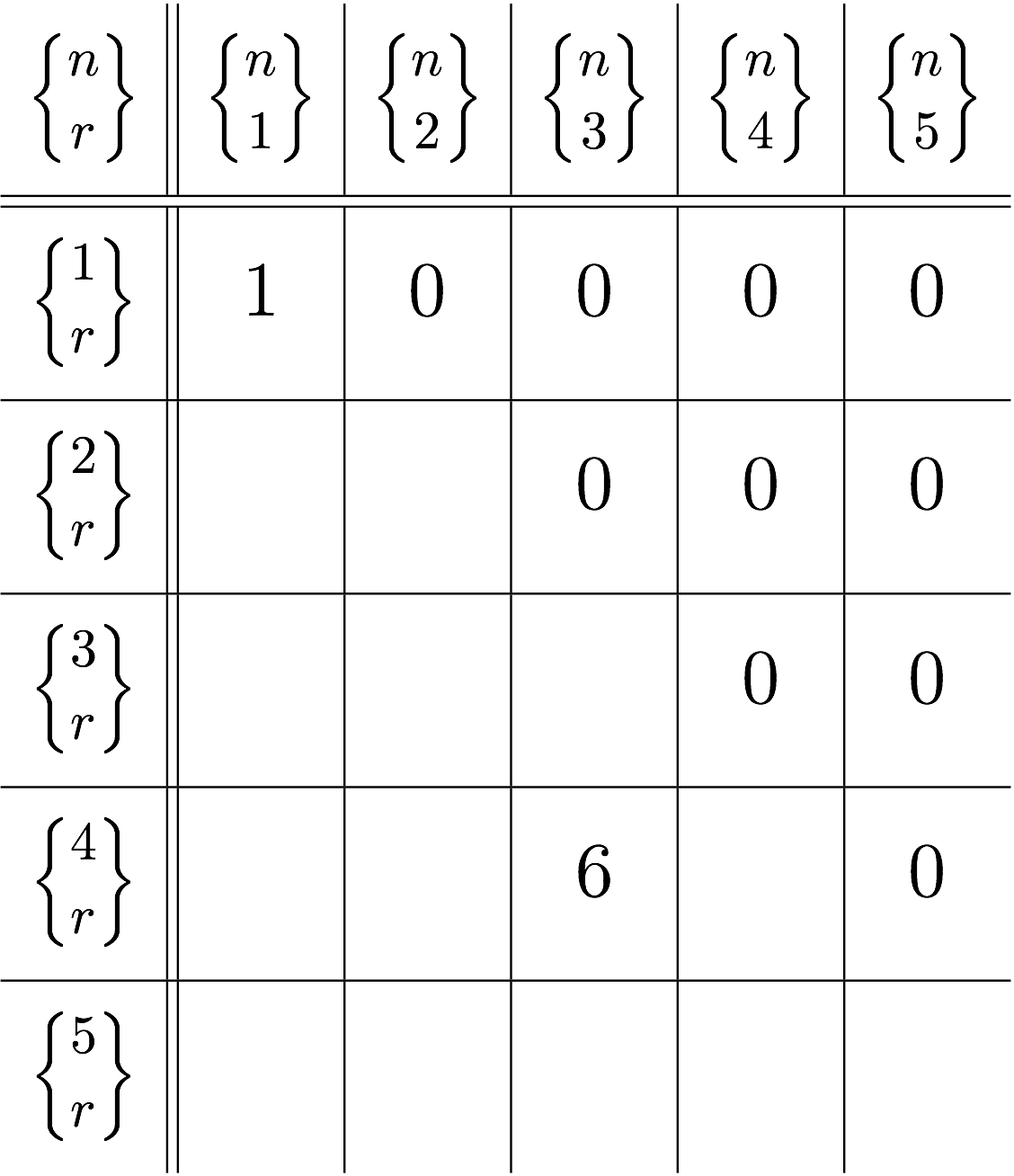
$$ \begin{align*} \SS{1,2,3,4} &= \SS{1,2}\cup\SS{3}\cup\SS{4} \\ &= \SS{1,3}\cup\SS{2}\cup\SS{4} \\ &= \SS{1,4}\cup\SS{2}\cup\SS{3} \\ &= \SS{1}\cup\SS{2,3}\cup\SS{4} \\ &= \SS{1}\cup\SS{2,4}\cup\SS{3} \\ &= \SS{1}\cup\SS{2}\cup\SS{3,4} \\ \end{align*} $$ のように全部で $6$ 通りに分割できる。 これを、 $$ \STIR{n}{r} = \STIR{4}{3} = 6 $$ と書くことにする。以下の表を完成させよ。
僕「なるほど。ミルカさんとテトラちゃんはこの問題を競争で解いているんだね」
返事はない。
テトラちゃんは、脇目も振らずにノートにガリガリと書き続けている。
その隣に並んで座っているミルカさんは、腕組みをして目を閉じている。
それにしてもこの二人が同じ問題を競争で解くっていうのはレアな状況だなあ。
そんなことを思いながら、僕もこの問題に興味を持ち始めた。 村木先生からのカードを読み返してみよう。 僕は二人の向かいの席に座る。
ええと……
ええと、まず $n$ と $r$ という二つの数が出てくる。 「$n$ と $r$ を $1$ 以上の整数とし」というのだから、 $n = 1,2,3,\ldots$ で、 $r = 1,2,3,\ldots$ ということ。
それから「集合 $\SS{1,2,3,\ldots,n}$」が出てくる。 《$1$ から $n$ までの整数を集めた集合》だな。
そしてこの集合を「$r$ 個の空ではない部分集合に分割」する。
うん、ここがポイントだな。
具体例を見てみよう。 村木先生は問題を出すときに、 誤解されないように例を出すことがある。 これも《例示は理解の試金石》の一種か。 出された例によって、自分の理解を確かめることができる。
ここに出てくるのは $n = 4, r = 3$ の例だ。
$n$ が $4$ だから、 $\SS{1,2,3,\ldots,n}$ という集合は、
$$ \SS{1,2,3,4} $$ になる。 $r$ が $3$ だから、 この $4$ 個の要素からなる集合を、 $3$ 個の部分集合に分割するわけだな。
僕はここでカードから目をそらし、 頭の中で $\SS{1,2,3,4}$ を $3$ 個に分割してみる。たとえば……
たとえば、これは $3$ 個の部分集合に分割している例の一つだ。
$$ \SS{1} \REMTEXT{と} \SS{2} \REMTEXT{と} \SS{3,4} $$
この分割では、 $3$ と $4$ が同じ部分集合に入ったけれど、 これと似たパターンがいくつかあるな。 $2$ と $4$ を一緒にした、こういうの。
$$ \SS{1} \REMTEXT{と} \SS{3} \REMTEXT{と} \SS{2,4} $$
あるいは、 $1$ と $3$ を一緒にした、こういうのも。
$$ \SS{2} \REMTEXT{と} \SS{4} \REMTEXT{と} \SS{1,3} $$
僕はここでカードに目を戻す。 そこには村木先生の例が書いてある。 なるほど……
$$ \begin{align*} \SS{1,2,3,4} &= \SS{1,2}\cup\SS{3}\cup\SS{4} \\ &= \SS{1,3}\cup\SS{2}\cup\SS{4} \\ &= \SS{1,4}\cup\SS{2}\cup\SS{3} \\ &= \SS{1}\cup\SS{2,3}\cup\SS{4} \\ &= \SS{1}\cup\SS{2,4}\cup\SS{3} \\ &= \SS{1}\cup\SS{2}\cup\SS{3,4} \\ \end{align*} $$
なるほど。和集合を表す $\cup$ を使って書いている。 全部で $6$ 通りの分割のしかたがある。 うん、ここまでで分割のしかたはよく理解したと思う。
村木先生のカードでは、この分割の《場合の数》に関心があるようだ。 カードでは $\STIR{n}{r}$ という表記法を使うと書かれている。 これは定義だからこのまま受け止めるしかない。
$n = 4, r = 3$ で、 $\SS{1,2,3,4}$ を $3$ 個の部分集合に分割する場合の数は $6$ 通りある。これを、
$$ \STIR{n}{r} = \STIR{4}{3} = 6 $$
のように書く……なるほど。
そして、問題はこの表を完成させることだ。

この表を見ると、すでに埋められているところがあるな。
まず目立つのは $0$ がたくさん並んでいるところ。 うん、これは $\STIR{n}{r}$ で $n < r$ のところだな。 そりゃそうだ。 《$n$ 個の要素を $r$ 個の部分集合に分割する》というのに、 要素の個数 $n$ よりも部分集合の個数 $r$ の方が多かったら、 そんな分割の仕方は存在しない。 分割しているうちに要素が足りなくなってしまうから。 だから、 $0$ だと。
$$ \STIR{n}{r} = 0 \qquad \textbf{($n < r$のとき)} $$
それから、表の一番左上。 $\STIR{1}{1}$ のところだ。 《$1$ 個の要素を $1$ 個の部分集合に分割する》というのは、 $\SS{1}$ の $1$ 通りしかない。だから $1$ だと。
$$ \STIR{1}{1} = 1 $$
そして、さっき具体的に数えた $\STIR{4}{3}$ のところ。 これは数えた通り $6$ だ。
$$ \STIR{4}{3} = 6 $$
さて、表の残りの空欄は……
僕がそこまで考えたところで、 ミルカさんが目を開け、表に数を一気に書き込んだ。
ミルカ「テトラ、できたよ。答え合わせをしよう」
テトラ「待ってください! 待ってください! $5$ の段がまだ途中で……」
僕「$5$ の段……ってまるで九九みたいだね」
ミルカ「では、テトラが先に話す」
テトラ「はい……あ、あたしはこの問題を読んだとき、最初のうちは意味がよくわかりませんでした。 でも、 $\STIR{4}{3}$ の例が書かれていたので、それを見て考えました」
$$ \begin{align*} \SS{1,2,3,4} &= \SS{1,2}\cup\SS{3}\cup\SS{4} \\ &= \SS{1,3}\cup\SS{2}\cup\SS{4} \\ &= \SS{1,4}\cup\SS{2}\cup\SS{3} \\ &= \SS{1}\cup\SS{2,3}\cup\SS{4} \\ &= \SS{1}\cup\SS{2,4}\cup\SS{3} \\ &= \SS{1}\cup\SS{2}\cup\SS{3,4} \\ \end{align*} $$
ミルカ「ふむ」
僕「例があると理解しやすいよね」
テトラ「はい……これを見てわかったのは、 この例の場合は《$1$ から $4$ までの整数を $3$ 個に分ける》ということです。 グループ分けというか」
ミルカ「部分集合への分割」
テトラ「はい。そして、条件に気付きました。分割したときに《部分集合の順序は考えない》という条件です」
ミルカ「ふむ」
テトラ「つ、つまり、 $\SS{1,2}\cup\SS{3}\cup\SS{4}$ という分割と、 $\SS{1,2}\cup\SS{4}\cup\SS{3}$ という分割とは同じものと見なす……んですよね?」
僕「そうみたいだね。それにしても、ちゃんとそういう条件を見つけるのってえらいなあ」
テトラ「は、はい! あたしもたまには《条件忘れのテトラ》の汚名返上ですっ!」
ミルカ「話を続ける」
テトラ「問題がわかってきたので、次にあたしは《小さな数で試す》を考えることにしました。 そして、表を眺めているうちに《すぐにわかるところがある》と気付きました」
ミルカ「トリヴィアルな場合」
テトラ「trivial? ……あ、そうですね。たとえば、 $r = 1$ のときはすぐにわかります。 だって《$1$ 個の部分集合に分割する》って《分割しない》ってことですから。 $\SS{1,2,3,\ldots,n}$ の $1$ 通りしかないですよね! だから、こうなります」
$$ \STIR{n}{1} = 1 $$
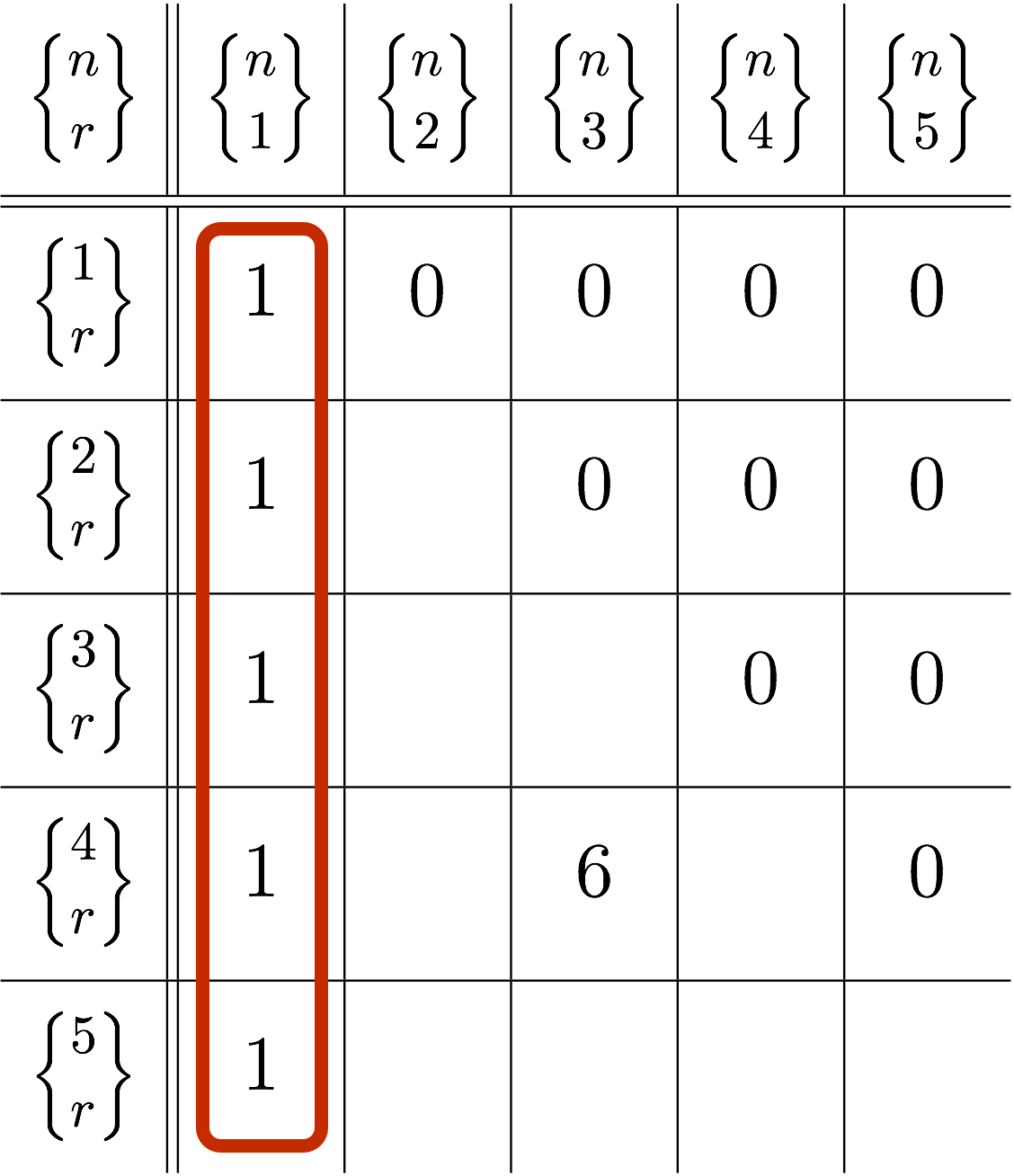
僕「うん、なるほど。これで縦のところが埋まるね」
$\STIR{n}{1} = 1$ で表を埋める
ミルカ「ここまで、テトラは私と同じ順序で考えている」
テトラ「え、そ、そうですか! うれしいです」
ミルカ「話を続ける」
テトラ「はい。続いて同じようにtrivialな場合を考えました」
僕「$n = r$ の場合だね。痛いっ!」
ミルカさんが向かい側の席から僕の足を蹴飛ばしてきた。 痛いなあ。
ミルカ「いまはテトラが発表中。話を先取りするな」
僕「あ……ごめん」
テトラ「はい。先輩がおっしゃったように、 $n = r$ の場合です。 要素の数 $n$ と分割する部分集合の数 $r$ が等しいわけですから、 これはつまり《全員ばらばら》になるしかありません。一人が一グループ。 これは $r = 1$ の場合の正反対ですね。 $r=1$ の場合には《全員いっしょ》でした。 でも、場合の数としてはどちらも $1$ 通りです」
$$ \STIR{n}{r} = 1 \qquad \textbf{($n = r$の場合)} $$
ミルカ「こう書いてもいい」
$$ \STIR{n}{n} = 1 $$
テトラ「両方に同じ $n$ ……なるほどです!」
僕「これで表の斜めが埋まったよ。空欄の残りは $5$ 個だね」
$\STIR{n}{n} = 1$ で表を埋める

ミルカ「ここまで、テトラは私と同じ順序で考えている」
テトラ「そうなんですね。だとしたらミルカさんの数えるスピードがものすごく速いということですね……」
ミルカ「私は数えていない」
テトラ「え?」
僕「え?」
ミルカ「いまはテトラの発表中」
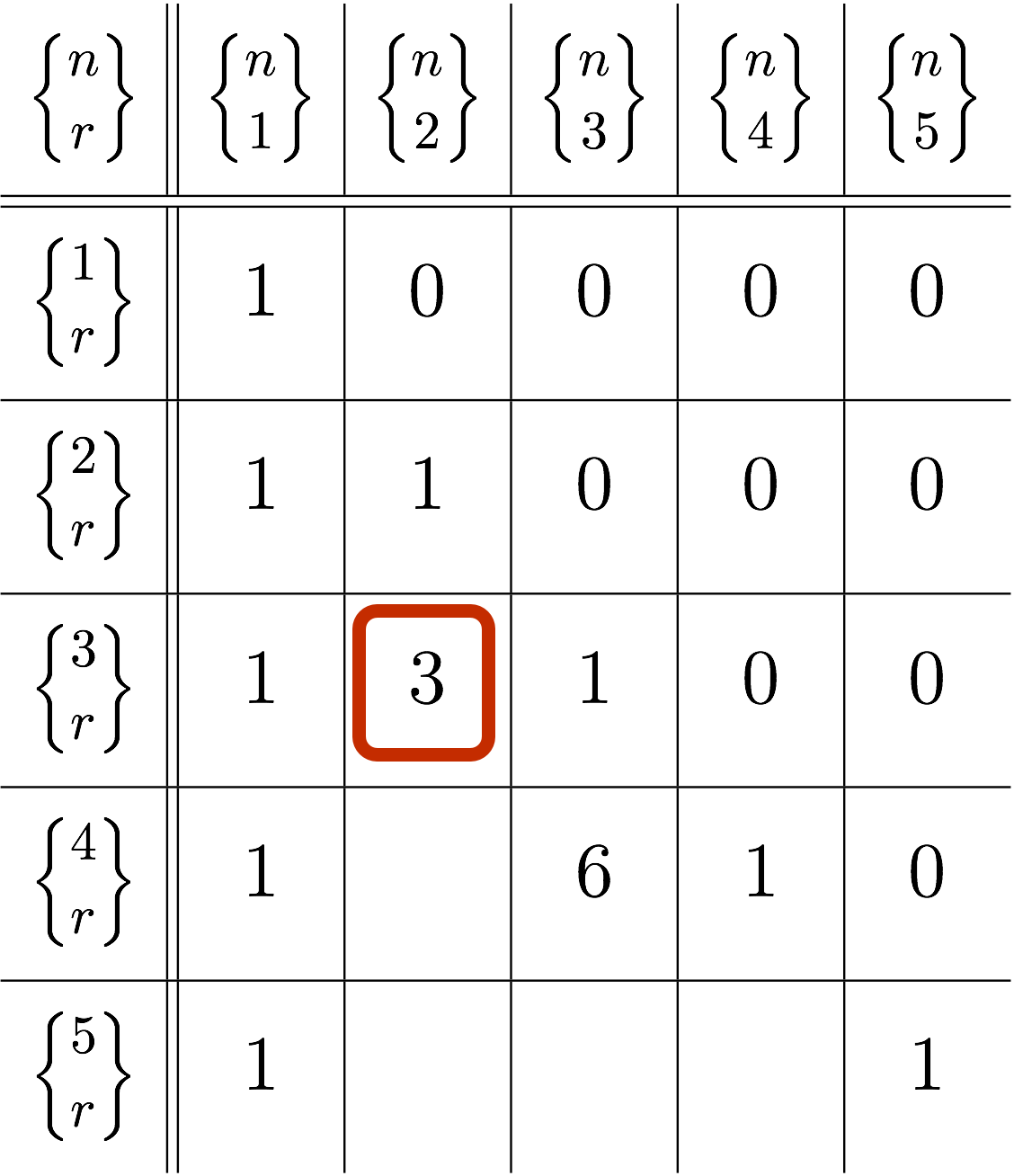
テトラ「は、はい……次にあたしがやったのは $n = 3, r = 2$ の場合を数え上げることでした。 村木先生からのカードにあった書き方にならって書くと、こうなります。 $3$ 通りになりました」
$$ \begin{align*} \SS{1,2,3} &= \SS{1,2}\cup\SS{3}\\ &= \SS{1,3}\cup\SS{2}\\ &= \SS{1}\cup\SS{2,3}\\ \end{align*} $$
$$ \STIR{3}{2} = 3 $$
ミルカ「ふむ」
僕「空欄が一つ埋まった」
テトラ「次は $n = 4, r = 2$ の場合です。 根気よく考えていくと、 $6$ 通りになりました」
$$ \begin{align*} \SS{1,2,3,4} &= \SS{1,2,3}\cup\SS{4}\\ &= \SS{1,2,4}\cup\SS{3}\\ &= \SS{1,2}\cup\SS{3,4}\\ &= \SS{1,3}\cup\SS{2,4}\\ &= \SS{1,4}\cup\SS{2,3}\\ &= \SS{1}\cup\SS{2,3,4}\\ \end{align*} $$
$$ \STIR{4}{2} = 6 \qquad \textbf{(?)} $$
ミルカ「違う。 $\SS{1,3,4}\cup\SS{2}$ が抜けている」
テトラ「えっ……あっ! ほんとですね。 $1$ 個足りませんでした」
$$ \begin{align*} \SS{1,2,3,4} &= \SS{1,2,3}\cup\SS{4}\\ &= \SS{1,2,4}\cup\SS{3}\\ &= \SS{1,3,4}\cup\SS{2} \qquad \textbf{←抜けていた} \\ &= \SS{1,2}\cup\SS{3,4}\\ &= \SS{1,3}\cup\SS{2,4}\\ &= \SS{1,4}\cup\SS{2,3}\\ &= \SS{1}\cup\SS{2,3,4}\\ \end{align*} $$
$$ \STIR{4}{2} = 7 $$
僕「惜しかったね。でもこれで、 $n \leqq 4$ の空欄はぜんぶ埋まったよ」

テトラ「そうですね……でも、あたしがたどり着いたのはここまでで、 $n = 5$ は場合分けの途中なんです。ミルカさん、先ほどおっしゃっていた《数えていない》というのは どういう意味ですか」
ミルカ「求められているのは分割そのものではなく、 分割の個数だ。《構造を見抜く》ことで個数がすぐにわかるところがある。 では、先ほどから空欄埋めをやっていた彼に答えてもらおう。 これはクイズだ。 $\STIR{5}{2}$ の値は?」
クイズ
$\STIR{5}{2}$ の値は?
僕「おっと、いきなり僕にふるのか……といっても、 数えてみないで構造が見抜けるわけないから、 僕は数えるよ」
ミルカ「好きに」
僕「ええと、全部で $5$ 個の要素を $2$ 個の部分集合に分割だから……」
$$ \begin{align*} \SS{1,2,3,4,5} &= \SS{1,2,3,4}\cup\SS{5}\\ &= \SS{1,2,3,5}\cup\SS{4}\\ &= \SS{1,2,4,5}\cup\SS{3}\\ &= \SS{1,3,4,5}\cup\SS{2}\\ &= \SS{2,3,4,5}\cup\SS{1}\\ &= \SS{1,2,3}\cup\SS{4,5}\\ &= \SS{1,2,4}\cup\SS{3,5}\\ &= \SS{1,2,5}\cup\SS{3,4}\\ &= \cdots \\ \end{align*} $$
僕「……まてよ?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年3月21日)
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!