![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
ここは僕の家のダイニング。 ユーリと僕はテレビを見ていた。 科学番組で映画"Powers of Ten"が紹介されている。 この十分足らずの映画では、最初に $1$ メートル四方の日常風景が写される。 そして、次第にカメラがその風景から遠ざかり、 十秒ごとに一辺の長さが $10$ 倍になっていくのだ。
ユーリ「……はふー。すごかったねー!」
僕「すごかったな……これが1977年の映画っていうのもすごいなあ」
ユーリ「これって、十秒ごとに $10$ 倍になってるんだよね」
僕「そうだね。映画の前半は、画面の一辺が十秒ごとに《$10$ 倍》になっていた。 後半になると逆に画面の一辺が十秒ごとに《$10$ 分の $1$》だったね」
ユーリ「宇宙がぐんぐん見えて、すごかったー」
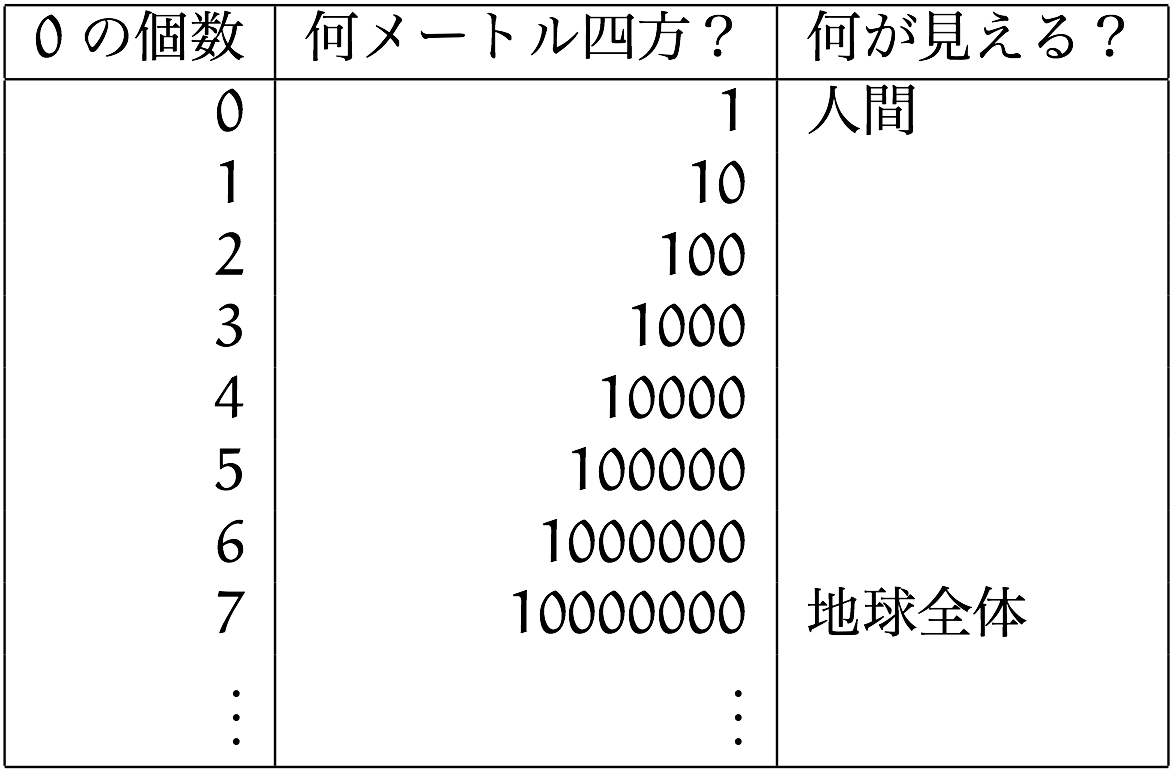
僕「うん、すごいよね。十秒ごとに《$10$ 倍》になるってことは、 $1$ の後に十秒ごとに $0$ をつけていくわけだね」
ユーリ「最初、ピクニックしてたよね」
僕「そうだったね。人間のサイズから、 $0$ を $7$ 個つけただけで地球全体くらいのサイズになるんだ」
ユーリ「$1$ の後に $0$ が $7$ 個って、何メートルになるの? いち、じゅう、ひゃく、せん……」
僕「一千万メートルだね。一万キロだ」
ユーリ「へー」
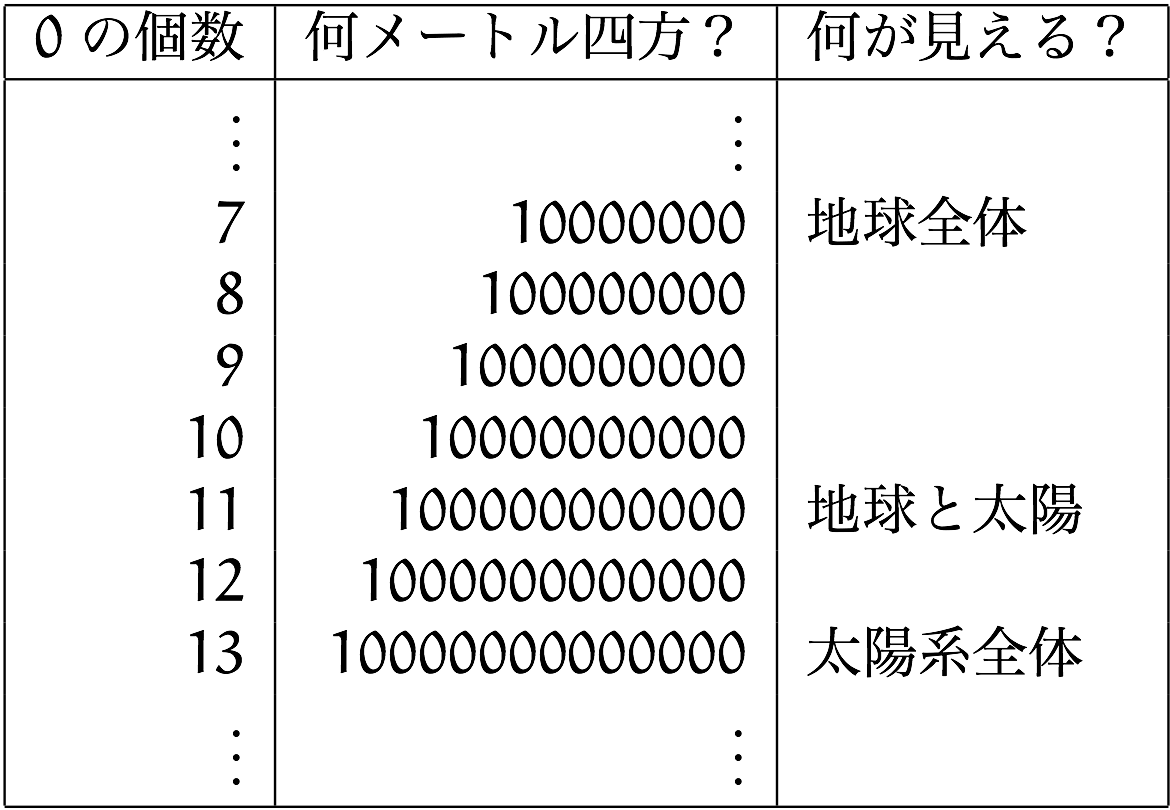
僕「$1$ の後に $0$ が $11$ 個つくと、太陽が画面に入ってきてた」
ユーリ「ちょっと待ってお兄ちゃん、なんでそんなの覚えてんの?」
僕「映画の右のほうに数字が出てたじゃないか。太陽が画面に入ってきたときは $10^{11}$ になってたよ」
ユーリ「いやいや、そんなの覚えてらんないって、ふつー」
僕「銀河系全体は $10^{21}$ メートル四方だったかな」

ユーリ「あのね、途中でめちゃ感動したのがね、 太陽系が星になったり、銀河系が星になったりするとこ」
僕「うん?」
ユーリ「ほらほら! 太陽系がどんどんちっちゃくなってたじゃん!」
僕「ああ……太陽系も、銀河系も、じゅうぶん離れると一つの星みたいだったってこと?」
ユーリ「そーそー! それと、逆に小さい方も宇宙みたい!」
僕「あれだろ? 原子の世界の中に入っていったとき。 小さい世界を見てるはずなのに、何だか宇宙を見てるみたいだったよね」
ユーリ「それからね、宇宙で、星が《集まってる》のもおもしろかった」
僕「集まっているって? 太陽系のこと?」
ユーリ「うん。たとえば太陽系は星が集まってるじゃん? でもしばらくすると今度は何にもない宇宙になって、 そんで、次は太陽系が集まった銀河系になって……でもまた何もない宇宙になる。 そーゆー《繰り返し》がおもしろかった!」
僕「銀河系全体が画面に入ったのは、 $10^{21}$ メートル四方だった」
ユーリ「$10$ の $21$ 乗って、 $1$ の後にゼロが $21$ 個続くんだよね?」
僕「そうだね。 $1,000,000,000,000,000,000,000$ メートルだ」
ユーリ「ふえー」
僕「$1000$ メートルはキロメートルだから、 わかりやすくいうと $1,000,000,000,000,000,000$ キロメートルだね」
ユーリ「いや、それ、ぜんぜんわかりやすくなってないから」
僕「あはは、そうだね。指数を使って表現したほうがいいか。 《銀河系の直径》がおおよそ $10^{21}$ メートルだとすると、 $10^{18}$ キロメートルになる」
$$ \begin{align*} \REMTEXT{《銀河系の直径》} &= 1000000000000000000000\REMTEXT{メートル} \\ &= 10^{21}\REMTEXT{メートル} \\ &= 10^{18}\REMTEXT{キロメートル} \\ \end{align*} $$
ユーリ「え? お兄ちゃん、いまどんな計算したの。 $21$ 乗から $18$ 乗」
僕「うん? $21$ から $3$ 引いたら $18$ だよ」
ユーリ「そんなのわかってる。何で $3$ 引いたの?」
僕「だって、 $1$ キロメートルは $1000$ メートル、つまり $10^3$ メートルだから、 $3$ 引けばいい」
$$ \begin{align*} 10^{21}\REMTEXT{メートル} &= 1\underbrace{000000000000000000000}_{\REMTEXT{$21$個}}\REMTEXT{メートル} \\ &= (1\underbrace{000000000000000000}_{\REMTEXT{$18$個}} \times 1\underbrace{000}_{\REMTEXT{$3$個}})\REMTEXT{メートル} \\ &= 1\underbrace{000000000000000000}_{\REMTEXT{$18$個}}\REMTEXT{キロメートル} \\ &= 10^{18}\REMTEXT{キロメートル} \\ \end{align*} $$
ユーリ「あー、そかそか。あたりまえじゃん」
僕「うん、これはちょうど指数法則の一例になっているよね」
ユーリ「しすーほーそく、って何だっけ」
僕「うん、たとえばこういうの。《全体の掛け算》は《指数の足し算》で計算できる」
指数法則の例(全体の掛け算は指数の足し算)
$$ \begin{align*} 1\underbrace{000000000000000000}_{\REMTEXT{$18$個}} \times 1\underbrace{000}_{\REMTEXT{$3$個}} &= 1\underbrace{000000000000000000000}_{\REMTEXT{$18+3 = 21$個}} \\ 10^{18} \times 10^{3} &= 10^{18+3} \\ \end{align*} $$
ユーリ「ふんふん。《$10$ の $18$ 乗》と《$10$ の $3$ 乗》を掛けると、 《$10$ の $21$ 乗》になるってことだね」
僕「そうそう。その $21$ という数は、 $18+3$ で求める。 これを《一般化》すると……」
ユーリ「ほらきた!」
僕「『ほらきた』って?」
ユーリ「ねえ知ってた? お兄ちゃんって、数学の話するとき必ず『一般化すると』って言い出すんだよー!」
僕「え、必ずってことはないと思うけどな」
ユーリ「いーや、違うね。必ずだね」
僕「まあ、だって、数学では《一般化》はとても大事だからしょうがないよ」
ユーリ「はいはい。では続けたまえ(にやにや)」
僕「$10^{18} \times 10^{3} = 10^{18 + 3}$ を一般化すると、こんなふうに書ける」
指数法則(全体の掛け算は指数の足し算)
$$ 10^{m} \times 10^{n} = 10^{m + n} $$
※ここで $m$ と $n$ は $1$ 以上の整数($1,2,3,\ldots$)とする。
ユーリ「ふんふん」
僕「さっきは $m = 18$ で $n = 3$ の例を話していたんだね」
ユーリ「そーだね」
僕「簡単な例を見るとすぐに意味はわかるよ」
ユーリ「もーわかったから、いーよ」
僕「そう? たとえば、 $m = 2$ で $n = 3$ とすると」
ユーリ「わかったって」
僕「$m = 2$ で $n = 3$ とすると、こうなって、確かにこの指数法則は成り立っている」
$$ \begin{align*} 10^{2} \times 10^{3} & = 100 \times 1000 \\ & = 100000 \\ & = 10^{5} \\ & = 10^{2+3} \\ \end{align*} $$
ユーリ「お兄ちゃん……ユーリが『わかっている』って言ってるのに、 最後まで説明し切るんだね……」
僕「説明を途中で止めるって苦しいんだよ」
ユーリ「掛け算したら《ゼロの個数》が足し算になるなんて、わかってるもん」
僕「ところでユーリ。さっき $10^m \times 10^n = 10^{m+n}$ を話したとき、 ※ここで $m$ と $n$ は $1$ 以上の整数($1,2,3,\ldots$)とするって条件つけたの、 なぜだか、わかる?
指数法則(全体の掛け算は指数の足し算)
$$ 10^{m} \times 10^{n} = 10^{m + n} $$
※ここで $m$ と $n$ は $1$ 以上の整数($1,2,3,\ldots$)とする。←コレ
ユーリ「え……そーいえば、なんで?」
僕「この条件をつけておけば、指数法則はこんなふうにして示せるからだよ」
指数法則が成り立つことを示す
$m$ と $n$ は $1$ 以上の整数($1,2,3,\ldots$)とする。
このとき《$10$ を何個掛けるか》を考えて次の式が得られる。
$$ \underbrace{10 \times \cdots \times 10}_{\REMTEXT{$m$個の$10$}} \times \underbrace{10 \times \cdots \times 10}_{\REMTEXT{$n$個の$10$}} = \underbrace{10 \times 10 \times \cdots \times 10}_{\REMTEXT{$m+n$個の$10$}} $$
このことから、 $$ 10^{m} \times 10^{n} = 10^{m + n} $$
が成り立つことがわかる。
ユーリ「ねー、これって《$10$ を何個掛けるか考えればいい》って意味でしょ?」
僕「そうだよ。《何個》っていうからには $1$ 以上の整数($1,2,3,\ldots$)でなくちゃまずいから、 だからああいう条件を付けたんだ」
ユーリ「わざわざまわりくどく言ってるみたい」
僕「そんなことないよ。それでね、いまは指数を《$1$ 以上の整数》で考えたよね」
ユーリ「うん」
僕「で、これを《$0$ 以上の整数》に拡張して考えよう」
ユーリ「えーと?」
僕「$10^0$($10$ のゼロ乗)を考えるってことだよ」
ユーリ「$10^0$ って $1$ でしょ? お兄ちゃん、こないだ言ってたじゃん」
$10$ の $0$ 乗は $1$ に等しい
$$ 10^0 = 1 $$
僕「うん、そうだよ。 $10^0$ は $1$ に等しいと定義されている」
ユーリ「てーぎ……」
僕「そう。ここが大事なところだよ、ユーリ。 $10^0$ を定義して、指数法則を拡張しているんだ」
ユーリ「うわあ……なにそれ」
僕「つまり、こういうことだよ。 $m$ と $n$ が $1$ 以上の整数ならば、それがどんな整数でも $10^m \times 10^n = 10^{m+n}$ は成り立つ」
ユーリ「それ、さっきやった」
僕「うん。そこでね、いま $10^0$ の値を定義したいんだけど、 どんな値として定義するのがいいかを考えたいんだ」
ユーリ「だって、 $10^0$ は $1$ って決まっているんでしょ?」
僕「そうだよ。でもそう決めたことには理由がある。 $10^0 = 1$ と定義するのが《うまい定義》だからなんだ」
ユーリ「うまい定義?」
僕「そう。《$m$ や $n$ が $0$ になるときでも、指数法則がちゃあんと成り立つ》という意味で、うまい定義」
ユーリ「ほほー……なるほど、わかんない」
僕「がく。じゃ、具体的に話そう。いま、 $m$ と $n$ が $0$ 以上の整数として、指数法則が成り立っているとしよう」
ユーリ「うん」
僕「だとすると、こういう式が成り立ってなくちゃいけない。指数法則で $m = 0,n = 1$ としたんだよ」
$$ \begin{align*} 10^m \times 10^n &= 10^{m+n} && \REMTEXT{指数法則} \\ 10^0 \times 10^1 &= 10^{0+1} && \REMTEXT{$m = 0, n = 1$とした} \\ 10^0 \times 10 &= 10 && \REMTEXT{$10^1 = 10$で$10^{0+1} = 10$だから} \\ 10^0 &= 1 && \REMTEXT{両辺を$10$で割った} \\ \end{align*} $$
ユーリ「ほほー」
僕「これ、何をやったかわかる?」
ユーリ「うん、わかる。 $10^0$ を求めたんでしょ」
僕「そう。だから、指数法則を満たすためには、 $10^0 = 1$ と定義しなければならなかったんだ」
ユーリ「……」
僕「じゃ、次に」
ユーリ「ちょっと待って、お兄ちゃん。ユーリのアンテナがぴぴっと……お兄ちゃんの説明、何だか変な気がする」
僕「え、いや、そんなことないと思うけどな。 $1$ 以上の整数で指数法則が成り立っているとき、 $0$ 以上の整数で成り立つように拡張したいなら、 $10^0 = 1$ と定義する必要がある」
ユーリ「えーとね、それはいーんだけど……ごめん、ちょっと待って。考える」
ユーリはちょっと目を細めるようにして思考モードに入った。 髪の毛が金色に一瞬輝いたかと思うと、にやっと笑った。
僕「で?」
ユーリ「やっぱ変だよ。お兄ちゃんは指数法則で $m = 0, n = 1$ として、 だから $10^0 = 1$ じゃなきゃだめだって言ったよね」
僕「うん、そういったよ」
ユーリ「でも指数法則が成り立つのを確かめたのは、 $m = 0, n = 1$ のときだけだよね? $m$ と $n$ が $0$ 以上の整数のとき、 絶対にいつでも指数法則は成り立つの?」
僕「おっと、そういうこと? ……確かに、さっきのお兄ちゃんの説明は少しまずかったな。 あれだと《指数法則が成り立つならば、 $10^0 = 1$ が成り立つ》しか言ってない。 逆に《$10^0 = 1$ が成り立つならば、指数法則は成り立つ》も言わなきゃまずいな。 まあ、でもそれはすぐに確かめられると思うけど」
ユーリ「そーなのか……」
僕「ところで、さっき指数法則を $0$ 以上に拡張したけど、整数全体に拡張するのも簡単だよ。 "Powers of Ten"の映画にも出てきてたけど」
ユーリ「映画に? 何が?」
僕「ほら、後半で《小さな数》を表すところで、 $10^{-1}$ や $10^{-2}$ が出てきたじゃないか」
ユーリ「あー、《$10$ のマイナス乗》のこと?」
僕「そうそう。ユーリは《$10^{-1}$ メートル》ってどれだけの長さか知ってる?」
ユーリ「えーとねー、なんだっけ……《$10$ 分の $1$ メートル》だっけ」
僕「そうだね。正解。《$10^{-1}$ メートル》は《$10$ 分の $1$ メートル》に等しい」
$$ 10^{-1} = \dfrac{1}{10} $$
ユーリ「あれだよね。 $10^{-2}$ だと $\dfrac{1}{100}$ なんだよね」
僕「そうだね。ユーリ、よく知ってるな」
ユーリ「前に一回教えてくれたじゃない、お兄ちゃん。忘れたの?」
僕「そうだったかな……これも、指数法則を拡張するという形で定義されるんだ」
ユーリ「$10^{-1}$ も?」
僕「そう。 $10^{-1}, 10^{-2}, 10^{-3}, 10^{-4}, \ldots$ 全部だね」
ユーリ「ふーん」
僕「たとえば、 $10^{-1}$ の値が何になるかを考えてみよう。 もちろん $\dfrac{1}{10}$ なんだけど、どうしてその値でなくちゃいけないかを考えるってことだよ」
ユーリ「ふんふん」
僕「指数法則が《すべての整数 $m$ と $n$ で成り立つ》ためには、 $10^{-1}$ はどんな値にならなくてはいけないかを考えたい。 いいかげんな値として定義しちゃったら、指数法則が成り立たなくなる。 それはいやだから、適切な値として定義したいということ」
ユーリ「……」
僕「どうした、ユーリ」
ユーリ「えっと、指数法則を成り立たせるための値を探すってこと?」
僕「そうだね」
ユーリ「ふーん」
僕「さっき $10^0$ の値を決めたときと同じように考えることになる。 今度は指数法則で $m = -1$ と $n = 1$ を入れてみよう。 もしも指数法則をすべての整数 $m$ と $n$ で成り立たせたいなら、 こうなるはず」
$$ \begin{align*} 10^m \times 10^n &= 10^{m+n} && \REMTEXT{指数法則} \\ 10^{-1} \times 10^1 &= 10^{(-1)+1} && \REMTEXT{$m = -1, n = 1$とした} \\ 10^{-1} \times 10 &= 10^{0} && \REMTEXT{$10^1 = 10$で$10^{(-1)+1} = 10^0$だから} \\ 10^{-1} \times 10 &= 1 && \REMTEXT{$10^0 = 1$だから} \\ 10^{-1} &= \dfrac{1}{10} && \REMTEXT{両辺を$10$で割った} \\ \end{align*} $$
ユーリ「ほほー!」
僕「ね? さっき $10^0$ を定義したときと同じように、 今度は $10^{-1}$ は $\dfrac{1}{10}$ として定義するのがいいってことがわかる」
ユーリ「そーだね。ちゃんとあってた」
僕「$10^{-1} = \dfrac{1}{10}$ と決まったら、 $10^{-2}$ も決まるよ。やっぱり指数法則を使う。 すべての整数で指数法則が成り立っているとしたら、 $10^{-2}$ は何になるかが自動的に決まるんだ。 $m$ と $n$ は何にしたらいいと思う?」
ユーリ「$10^{-2}$ を求めるんだよね……そりゃ、 $m = -1$ で $n = -1$ じゃないの?」
僕「やってみよう」
$$ \begin{align*} 10^m \times 10^n &= 10^{m+n} && \REMTEXT{指数法則} \\ 10^{-1} \times 10^{-1} &= 10^{(-1)+(-1)} && \REMTEXT{$m = -1, n = -1$とした} \\ \dfrac{1}{10} \times \dfrac{1}{10} &= 10^{(-1)+(-1)} && \REMTEXT{$10^{-1} = \dfrac{1}{10}$だから} \\ \dfrac{1}{10} \times \dfrac{1}{10} &= 10^{-2} && \REMTEXT{$10^{(-1)+(-1)} = 10^{-2}$だから} \\ \dfrac{1}{100} &= 10^{-2} && \REMTEXT{$\dfrac{1}{10} \times \dfrac{1}{10} = \dfrac{1}{100}$だから} \\ 10^{-2} &= \dfrac{1}{100} && \REMTEXT{両辺を交換した} \\ \end{align*} $$
ユーリ「ねーお兄ちゃん。これって《繰り返す》ことができるよね」
僕「そうだね。 $10^{-1}$ で $10^{-2}$ を作ったのと同じように、 $10^{-1}$ と $10^{-2}$ で $10^{-3}$ が作れる。 それを繰り返していけば……」
$$ \begin{align*} 10^{0} &= 1 \\ 10^{-1} &= \dfrac{1}{10} \\ 10^{-2} &= 10^{-1} \times 10^{-1} = \dfrac{1}{10} \times \dfrac{1}{10} = \dfrac{1}{100} \\ 10^{-3} &= 10^{-1} \times 10^{-2} = \dfrac{1}{10} \times \dfrac{1}{100} = \dfrac{1}{1000} \\ 10^{-4} &= 10^{-1} \times 10^{-3} = \dfrac{1}{10} \times \dfrac{1}{1000} = \dfrac{1}{10000} \\ 10^{-5} &= 10^{-1} \times 10^{-4} = \dfrac{1}{10} \times \dfrac{1}{10000} = \dfrac{1}{100000} \\ &\vdots \\ \end{align*} $$
僕「そして、これを……」
ユーリ「《一般化》するんでしょ?」
僕「あ!」
ユーリ「ほらきた! ね、必ず言うじゃん?」
僕「確かに……ともかく、一般化するとこうなる。 $n$ を $0$ 以上の整数($0,1,2,3,\ldots$)とする」
$$ \begin{align*} 10^{0} &= 1 \\ 10^{-1} &= \dfrac{1}{10^1} = \dfrac{1}{10} \\ 10^{-2} &= \dfrac{1}{10^2} = \dfrac{1}{100} \\ 10^{-3} &= \dfrac{1}{10^3} = \dfrac{1}{1000} \\ 10^{-4} &= \dfrac{1}{10^4} = \dfrac{1}{10000} \\ 10^{-5} &= \dfrac{1}{10^5} = \dfrac{1}{100000} \\ &\vdots \\ 10^{-n} &= \dfrac{1}{10^n} = \dfrac{1}{1\underbrace{000\cdots0}_{\REMTEXT{$n$個}}} \\ \end{align*} $$
ユーリ「おっけー」
《$10$ の $-n$ 乗》
$$ 10^{-n} = \dfrac{1}{10^n} = \dfrac{1}{1\underbrace{000\cdots0}_{\REMTEXT{$n$個}}} $$
※ただし、 $n$ を $0$ 以上の整数($0,1,2,3,\ldots$)とする。
ユーリ「お兄ちゃん。さっき、銀河系って直径どのくらいって言ったっけ」
僕「$10^{21}$ メートルって言ってたね」
$$ 10^{21}\REMTEXT{メートル} = 1000000000000000000000\REMTEXT{メートル} \qquad \REMTEXT{(銀河系全体の直径)} $$
ユーリ「こんなんだと、もう大きいんだか小さいんだかわかんないよね」
僕「いやいや、すごく大きいと思うよ」
ユーリ「そーだけどさ」
僕「《指数を使った数の表現》がすごいのは、 $1000000000000000000000$ なんていうすごく大きな数を、 $10^{21}$ のように短くまとめて書けるところにあるよね」
ユーリ「短くまとめても、同じ数なんでしょ?」
僕「うん。でもね、たくさんある $0$ の数をいちいち数えなくても、 $10^{21}$ を見ればゼロが $21$ 個あるってわかるじゃないか」
ユーリ「? あたりまえじゃん?」
僕「たとえば、次の二つの数はどっちが大きい?」
どちらが大きいか?
$$ 1000000000000000000000 \qquad 10000000000000000000000 $$
ユーリ「うわひどい問題! 目がちらちらしてわかんないよ」
僕「だよね。確かにひどい問題だ。でもこれならどう?」
どちらが大きいか?(指数を使った表現)
$$ 10^{21} \qquad 10^{22} $$
ユーリ「おー、なるほど。そりゃ $10^{21}$ より $10^{22}$ のほうが大きいよ」
僕「ね、だから、すごく《大きな数》を扱うときには、 《指数を使った表現》はとても便利だってことがわかるだろ」
ユーリ「それはそーみたいだけど……ひっかかるにゃ」
僕「何が?」
ユーリ「確かに、 $1000000000000000000000$ みたいに $0$ が《繰り返し》出てくるような数だったら、 $10^{21}$ って短く書けるからいいけど、そんな数ばっかりじゃないじゃん!」
僕「うん、それはそうか。ユーリの言うのも正しいな。 $10^{21}$は$\underbrace{10 \times 10 \times \cdots \times 10}_{\REMTEXT{$10$が$21$個}}$という形をしているから、 大きな数でも短く表せると」
ユーリ「そゆこと。何かを繰り返して作った数ならいーんだけど……あ!」
僕「なに?」
ユーリ「あのねお兄ちゃん。ユーリ、おもしろいこと思いついた!」
僕「?」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第71回終わり)
(2014年4月11日)