![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
ユーリ「……それで、微分していくと、最後はグラフが平らになるんだね」
僕「どういうこと?」
ユーリ「だってそーじゃん。 $n$ 回微分したら定数になっちゃうんでしょ? 定数ならグラフは水平線。平らじゃん」
僕「ああ、そうだね。多項式で作られた関数の場合には、確かにそうなる」
ユーリ「え?」
僕「ユーリのいう通り $n$ 回微分したら定数になるよ」
ユーリ「違う違う。いまなんで《多項式で作られた関数の場合には》って、わざわざ条件を入れたの?」
僕「それは、いくら微分しても定数にならない関数というものがあるからだよ!」
ユーリ「へ? そんなわけないじゃん」
僕「ばっさり言い切ったな、ユーリ。どうして《そんなわけない》なんて言い切れるんだろう」
ユーリ「だって、そーじゃん。お兄ちゃんが言ったんだよ。 $x^n$ を $x$ で微分すると、 $nx^{n-1}$ になるって。 いまそー教えてくれたばかりじゃん! 微分すればどんどん指数が小さくなるんじゃないの?(第47回参照)」
僕「うん、だからそこで多項式で作られた関数かどうかが重要になってくるんだよ」
ユーリ「あ」
僕「多項式で作られた関数というか、多項式で表せる関数といった方がいいかな。 多項式で表せる関数だったら、ユーリのいう通り、 $n$ 次関数は $n$ 回微分したら定数になってしまう。 確かにそれはそうだよ。 でも、多項式で表せない関数には、何回微分しても定数にならないものがある」
ユーリ「へー」
僕「たとえば、三角関数はそうだね」
ユーリ「サインとかコサインとか?」
僕「お、ユーリ、よく知ってるな」
ユーリ「馬鹿にしないでほしいにゃ。お兄ちゃんよく言ってるじゃん」
僕「たとえばサイン。 $\sin x$ という $x$ の関数は $x$ で何回でも微分できるし、 何回微分しても定数にはならないんだよ」
ユーリ「サインってこーゆーやつでしょ?」
僕「そうそう……だいたいはね。サインカーブはもっときれいだけど」
ユーリ「言ったな! じゃーお兄ちゃん描いてみてよ」
僕「現役高校生なめるんじゃないぞ……こうかな。あ、横軸 $\theta$ にしちゃったけど」
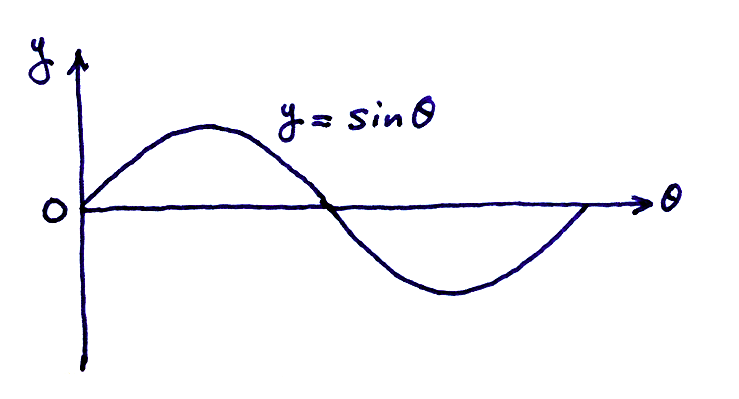
ユーリ「たいして変わんないじゃん」
僕「いやいやいやいや。ぜんぜん違うよ。 ちゃんと大きさも意識して描いているし、ポイントを押さえているし」
ユーリ「ポイントって?」
僕「サインカーブを描くポイント」
ユーリ「へー、何その《$1.5$ くらい》とか《$3$ ちょっとのところ》って」
僕「$1.5$ くらいっていうのは円周率 $3.14\cdots$ の半分のことだし、 $3$ ちょっとのところっていうのは円周率のこと」
ユーリ「あー、円周率が出てくるんだ!」
僕「そうだよ」
ユーリ「なんで」
僕「何でって……あ、ユーリはラジアン習ってないんだっけ」
ユーリ「らじあん?」
僕「角度の単位だよ。三角関数を使うときは角度の単位にラジアンを使うと便利なんだ」
ユーリ「角度の単位って……度じゃないの? $180$ 度とか、 $360$ 度とか」
僕「うん、《度》も角度の単位だね。《ラジアン》も角度の単位。 $180$ 度は $\pi$ ラジアンに相当する」
ユーリ「ぱいらじあん?」
僕「そう。つまり $180$ 度イコール $3.14159265\cdots$ ラジアンということ」
$$ 180~\REMTEXT{度} = \pi~\REMTEXT{ラジアン} $$
ユーリ「へー」
僕「$180$ 度の $2$ 倍が $360$ 度だよね。だから、 $360$ 度は $\pi$ ラジアンを $2$ 倍した $2\pi$ ラジアンになる」
$$ 360~\REMTEXT{度} = 2\pi~\REMTEXT{ラジアン} $$
ユーリ「へえ……そんな、 $3.14\cdots$ ラジアンみたいな単位だと割り切れなくてたいへんじゃないの?」
僕「普段は $3.14\cdots$ ラジアンのように円周率の数字を生で出すことはなくて、 $\pi$ ラジアン($180$ 度)や、 $2\pi$ ラジアン($360$ 度)のように $\pi$ を使って表すからね」
ユーリ「だったら、 $90$ 度は何ラジアンなの?」
僕「$180$ 度が $\pi$ ラジアンなんだから、 $90$ 度は何ラジアンだと思う?」
ユーリ「半分」
僕「うん、そうだね。 $180$ 度は $\pi$ ラジアンだから、 $90$ 度はその半分で $\frac{\pi}{2}$ ラジアン」
ユーリ「うわ分数使うんだ」
僕「そうだね。同じように $60$ 度は $\frac{\pi}{3}$ ラジアン」
ユーリ「うわめんど」
僕「いやいや、何度も扱っているうちにすぐ慣れるよ。たとえば正三角形のひとつの角度は、 $60$ 度だけど、 $\frac{\pi}{3}$ といわれてもぜんぜん違和感ない」
ユーリ「そーゆーもんなんだ」
僕「半径が $1$ の円で弧(こ)を考えると、ちょうど中心角をラジアンで表したときの数が、弧の長さに等しくなるんだよ」
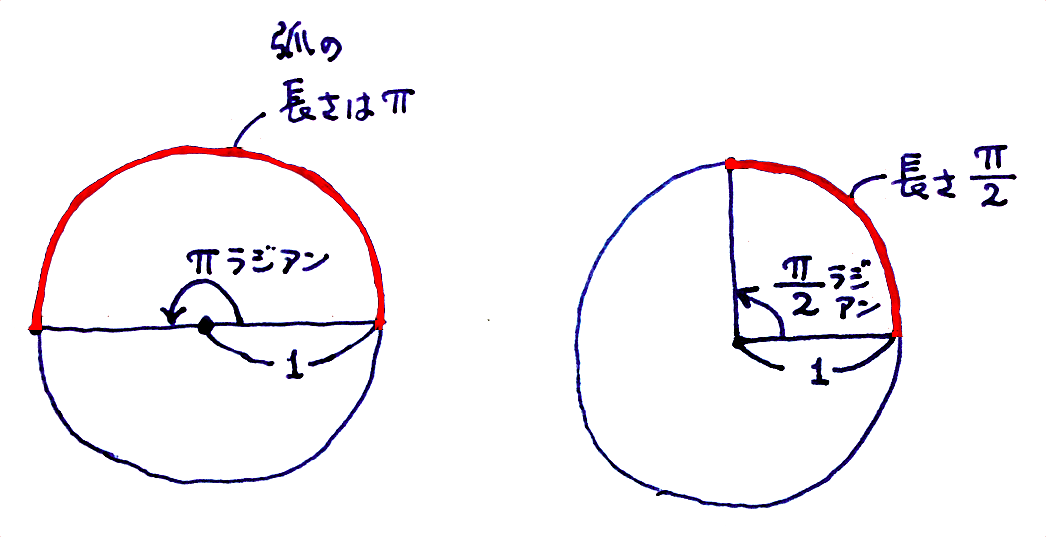
ユーリ「へー」
僕「ぐるっと一回りを $360$ 度って決めたのはたぶん、 $360$ がたくさんの約数を持っていたからだと思うんだ。 つまり、人間の生活に便利なように定めたんだね。 ラジアンは、円の弧長と中心角が対応するように決められているから、円そのもので定義したって感じがするんだよ」
ユーリ「そーかなー」
僕「ともかく、これがラジアン。角度の単位だ。そして $x$ が $0$ から $2\pi$ ラジアンまで動くとき、 $\sin x$ はひとつの波を描く。 $1$ 周期だね」

ユーリ「ねーお兄ちゃん。ユーリにもっかいサインカーブ描かせてよ。お兄ちゃんよりきれいに描くから!}
僕「どうぞどうぞ」

ユーリ「難しーもんだねー……」
僕「お兄ちゃんはしょっちゅう描いているからね」
ユーリ「うー、なんか悔しいにゃ」
僕「ところで、サインの微分……つまり、 $\sin x$ を $x$ で微分したらどうなるかだけど」
ユーリ「難しい話?」
僕「いやいや、難しくはないよ。ユーリは微分がどういうものか、もう知ってるから、 グラフをながめながら説明しよう。 微分の定義を使って計算でも求められるんけど、そっちはまた今度」
ユーリ「グラフ?」
僕「うん。サインカーブを描いているときって、こう……カーブに沿って手を動かすから、 つい勘違いしてしまうけど、本当はこんな縦線の集まりだと考えた方がわかりやすいよ」

ユーリ「どゆこと?」
僕「つまり、 $x$ の値が決まると、 $y$ の値が決まるということをしっかりと思い出すってこと。 それが関数だからね。そして、《$x$ が少し増えたときに $\sin x$ はどれだけ増えるかな》と考える」
ユーリ「あ、そーいえば、前もそんな話あったよね。えーと……瞬間の変化率だっけ?」
僕「そうそう。多項式で表される関数だろうが、三角関数だろうが、関数を微分するというのはいつも同じ。 瞬間の変化率を考えることになる。 ただ、瞬間の変化率というと、横軸が時間という印象が強くなっちゃうけどね」
ユーリ「でもそのほーがわかりやすかったよ。位置のグラフから速度のグラフを作る」
僕「そうだね。それで考えてみたほうがいいかな。 《$t$ が少し増えたとき、 $\sin t$ はどれだけ増えるか》を考える。それで $\sin t$ の増加分を $t$ の増加分で割る。比を求めるわけだ」
ユーリ「うん」
僕「実際に少しやってみよう。たとえば $t = 0$ のときと、 $t=\frac{\pi}{2}$ のときの変化率はこんな感じだ」
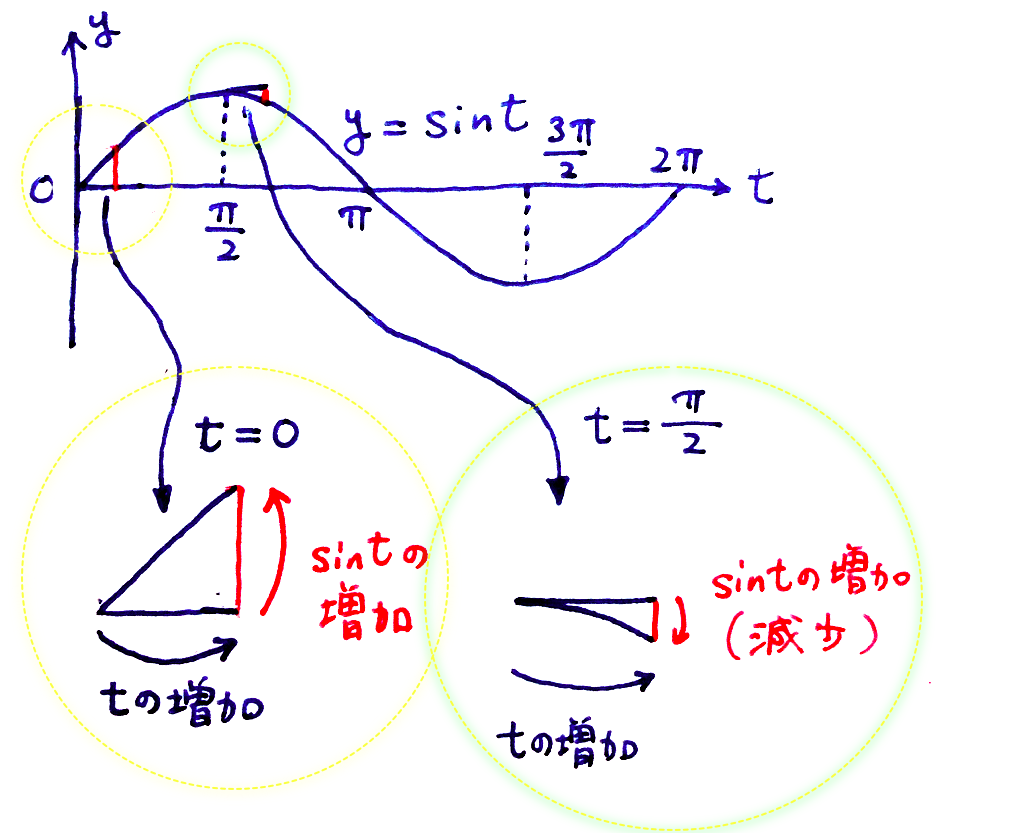
ユーリ「……」
僕「$t=0$ のときは直角二等辺三角形になるから、 $\sin t$ の増加分と $t$ の増加分は等しい。だから変化率は $1$ になる」
ユーリ「ふーん」
僕「それから、 $t = \frac{\pi}{2}$ のとき、変化率はすごく $0$ に近くなる。この図ではちょっぴり下がっているけど」
ユーリ「ほほー。ねーお兄ちゃん。これって、 $t$ が $0$ のときはぐいっと増えるけど、 $t$ が、二分のパイのときは、ほとんど減らないってことだよね」
僕「そうそう。そういう変化の度合いをグラフから読み取れればいい」
ユーリ「ふむふむ」
僕「そういう変化の様子を、 $t = 0$ から $t = 2\pi$ まで見ていくとこんな感じになる」
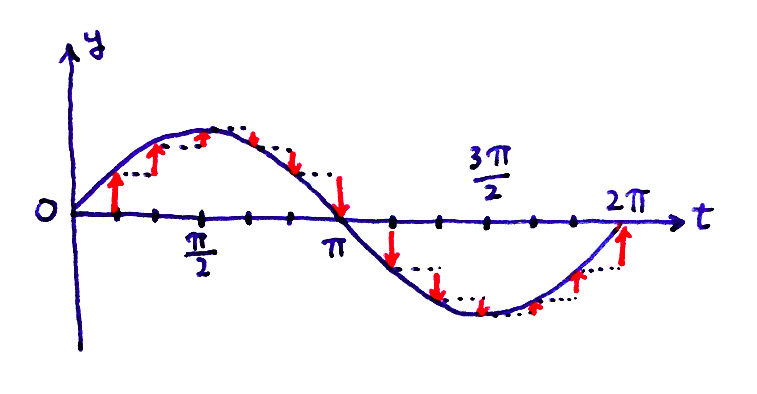
ユーリ「うわ、ちまちました図……だけど、うん、わかる」
僕「$t = 0$ から $t = \frac{\pi}{2}$ までの変化率は、 $1$ から $0$ までだんだん小さくなっていく」
ユーリ「ふんふん。 $1$ と $0$ ってゆーのはさっき見たところだね」
僕「そう。それから $t = \frac{\pi}{2}$ から $t = \pi$ までの変化率をみてみると、 $0$ から $-1$ までだんだん小さくなっていく」
ユーリ「だんだん下がっているし」
僕「その次は $t = \pi$ から $t = \frac{3\pi}{2}$ までの変化率を見ると、 $-1$ から $0$ までだんだん大きくなる」
ユーリ「その次はわかるよ! $0$ から $1$ まで大きくなるんでしょ?」
僕「そうだね。いまはこんな手描きのグラフでざっくりと変化率を見たけど、そこからこんなふうに増減表を書いてみよう」
ユーリ「ぞーげんひょー?」
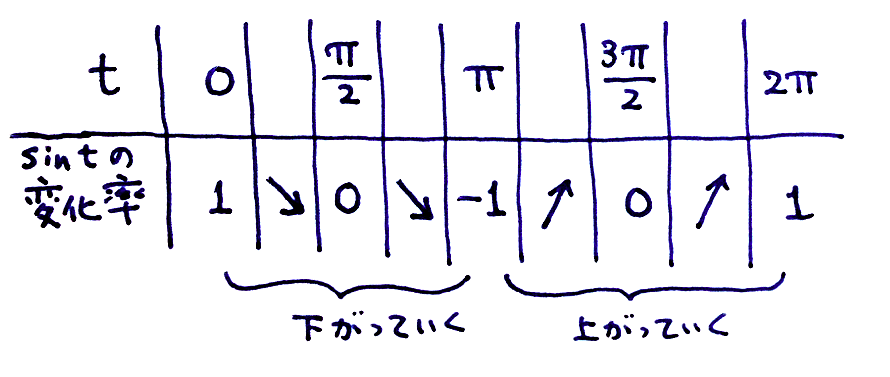
僕「そしてね、この増減表から、《$\sin t$ という関数を $t$ で微分したときの、導関数のグラフ》の形がぼんやりと見えてくる」
ユーリ「へー」
僕「いや、《へー》じゃなくて、どんな形をしているか、ユーリならわかるだろ?」
ユーリ「あ、ユーリが描くのか。えーとねー。 $0$ んとき $1$ で、そこからぐっと下がって $0$ になって、ずっと下がって $-1$ で、戻ってきて $0$ ……あれ?」
僕「わかった?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年9月27日)
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!