![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
ユーリ「お兄ちゃん、ビブンって何?」
僕「え? 微分って、このあいだ話したばかりじゃないか」
従妹のユーリは中学生、 しょっちゅう僕の部屋にいりびたっている。 今日はいきなり質問だ。 でも、微分については先日ずいぶんたくさん教えたと思うんだけどな……(第44回参照)
ユーリ「そーだけど、今度は微分の微分をちゃっちゃと教えてよ!」
僕「微分の微分? また友達と競ってるんだね」
ユーリには数学好きの友達がいて、 よく問題を解き合ったりしているらしい。 けっこう本を読む友達らしく、難しい数学の話をユーリにしているようだ。
ユーリ「そーゆーセンサクはいいから、早く教えてよ」
僕「なんだかデジャヴだな。 ユーリはもう微分がどんなものなのかイメージとしてわかっているから、 《微分の微分》なんてすぐわかると思うよ。簡単にいえば、微分してからもう一度微分することだね」
ユーリ「それだけのこと?」
僕「簡単にいえばね」
ユーリ「わかった、ありがと。じゃーね」
僕「ちょちょ! ちょっと待った」
ユーリ「どしたの」
僕「ほんとうにわかったのかなあ……このあいだは《位置》と《速度》を使って微分の話をしたよね」
ユーリ「うん、そーだった。動点 $P$ の話がやたらくどかった」
僕「悪かったよ……」
ユーリ「でも、グラフの話はよくわかったよ。さすがお兄ちゃん。《位置のグラフ》から《速度のグラフ》を作り出すのが微分でしょ」
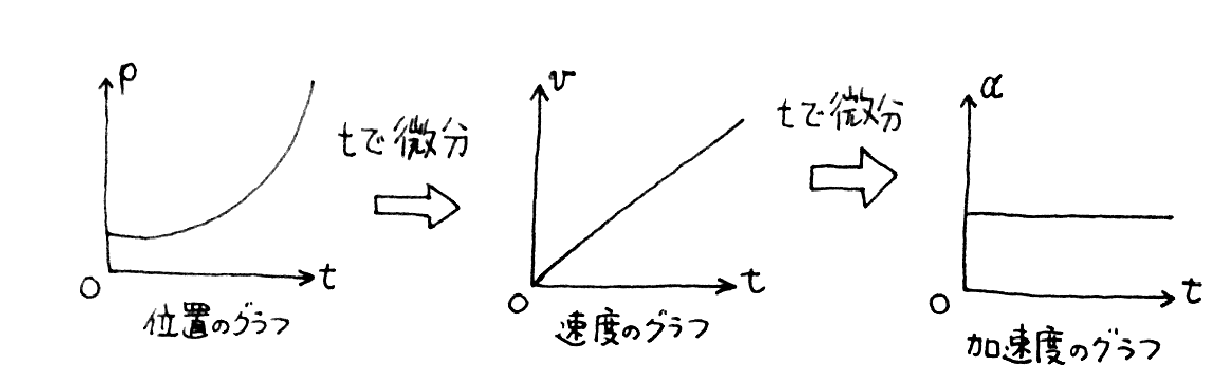
僕「そうだね。よくわかってるなあ。《位置のグラフ》を時間で微分すると《速度のグラフ》ができる」
ユーリ「うん」
《位置のグラフ》を時間で微分して《速度のグラフ》を得る

僕「それで、ユーリがさっき言ってた微分の微分だけど、《速度のグラフ》をさらに時間で微分すると《加速度のグラフ》ができる」
ユーリ「かそくど?」
僕「そうだよ。《位置》を微分すると《速度》で、《速度》を微分すると《加速度》になる。 だから、《位置》を $2$ 回微分すると《加速度》ということ」
《位置のグラフ》を $2$ 回微分して《加速度のグラフ》を得る
ユーリ「ふんふん」
僕「加速度は、車に乗ったときによく感じるからわかるよね」
ユーリ「うん。車が発車するときにギュウっと後ろに引っ張られる感覚のことでしょ?」
僕「そうそう。あれは加速度を感じてるんだね」
ユーリ「あと、止まるとき。急ブレーキかかると前にドーンとのめったり」
僕「うん、そう。それも加速度だ。なんだ、よくわかっているじゃないか」
ユーリ「へへ」
僕「じゃあ、ユーリにクイズだよ。 新幹線で走っている途中はすごいスピードなのに、 どうしてギュウっと後ろに引っ張られたり、前にドーンとのめったりしないのか」
ユーリ「え?」
僕「新幹線は車なんかよりずっと速いのに、どうしてそれほど加速度を感じないのかということ」
ユーリ「あれ……そーいえばそーだね。えーと」
僕「それはね」
ユーリ「ちょっと待ってよ! ……たぶん、加速が少ないから?」
僕「うん、だいたいそれで正解。加速が少ないというのは、速度の変化が小さいという意味だね。 速度の変化が小さいというのは加速度が小さいってことだ」
ユーリ「うん」
僕「速度と加速度を区別するのはとても大事なことだよ。 車が発車するときは速度はまだ小さいけれど、加速度は大きい。 遅くても、速度が急に大きくなるという意味」
ユーリ「速度は小さいけど……加速度は大きい。ふんふん」
僕「それに対して、新幹線が走っている最中の速度はとても大きいけれど、速度の変化である加速度は小さい」
ユーリ「そかそか。今度は速度は大きいけど、スピードがずーっと変わんないってことでしょ?」
僕「その通り!」
ユーリ「わかった」
僕「僕たちは、速度を感じることはできない。 僕たちが感じることができるのは、速度じゃなくて加速度なんだ」
ユーリ「え! 速度って感じられないの? だって、自転車乗ってたら風を感じるよ。 スピード上げたら風の抵抗が大きくなるし」
僕「確かにそうだね。お兄ちゃんが《速度を感じることはできない》って言ったのは、直接は感じることはできないという意味。 風のようなもので速度を間接的に感じることはできるよ」
ユーリ「カンセツ的に感じる……え、ちょっと待ってよ。加速度だってそうじゃないの?」
僕「いやいやいや、違うよ。車の発車でぐいっと後ろに引っ張られるのは風の力じゃないよね」
ユーリ「……そっか」
僕「車や新幹線や飛行機、何でもいいけど速度が大きい乗り物に乗ったとき、 速度がどんなに大きくても、僕たちは何も感じない。その速度が変化しない限りね。 速度が変化するとき、僕たちはそれを感じる。乗り物の中で、たとえばトイレでもいいや、 周りの景色が何も見えなくて、風もまったく入らないような状況でも、速度が変化したら僕たちはそのことがわかる。 僕たちが感じるのは速度じゃない。加速度なんだ」
ユーリ「ふーん」
僕「それに、僕たちが生活しているこの地球だって、ものすごい速度で動いているけれど、僕たちはそれをまったく感じないで生活しているね」
ユーリ「あ!」
僕「ねえユーリ。ところで微分の微分でどんな勝負をしているの? いつもの友達?」
ユーリ「ん? いや別に勝負ってわけじゃないんだけど」
僕「うん」
ユーリ「ほら、こないだお兄ちゃんから微分の計算の話きいたじゃん? 《$t^2$ を $t$ で微分して $2t$ を得る》って計算もやったし(第44回参照)」
僕「ああ、そうだったね。手で計算した」
ユーリ「その話をあいつ……友達にしたら、《$2t$ をさらに微分したら $2$ になるな》とかすぐ言われた。それから微分の微分がどーこー言われた」
僕「確かにそうだね。それにしても中学生同士で微分の計算対決してるのか」
ユーリ「そんなに微分の計算って早くできるもんなの?」
僕「$t^2$ や $2t$ みたいな簡単な式……多項式で表されてる関数の微分はすぐにできるよ。 微分の定義から計算するのはやっかいだけど、その結果だけ使うなら中学生でもぜんぜん難しくない」
ユーリ「えー、なんでそれこないだ教えてくんなかったの!」
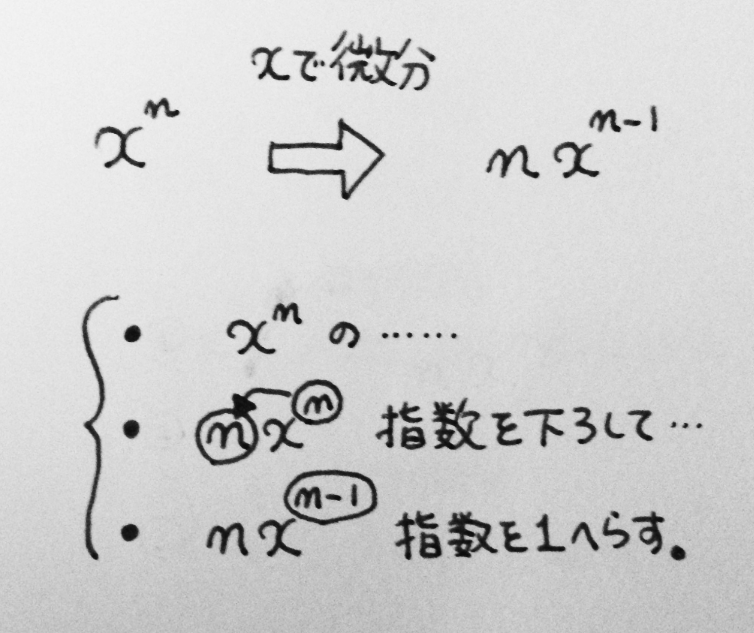
僕「何でって言われても……ともかく、基本は $x^n$ の微分だよ。 $x^n$ を $x$ で微分するときには、 指数の $n$ を係数のところに下ろしてきて、指数の $n$ を $n-1$ に変えればいい。 そうすれば $x^n$ から $nx^{n-1}$ が出てくる」
《$x^n$ を $x$ で微分すると $nx^{n-1}$ になる》
ユーリ「ふーん」
僕「……あれ?」
ユーリ「お兄ちゃん……どーしたの?」
僕「いや、似たような話を最近テトラちゃんにしたなあと思って」
ユーリ「テトラさん『ユーリちゃんって、可愛らしい中学生なのに、もう微分なんてやってるんですか?』とか言ってた?」
僕「言ってた言ってた。『可愛らしい』という形容詞があったかどうかは覚えてないけど」
ユーリ「むー」
僕「ともかく、 $x^n$ の微分ができれば、簡単な関数はすぐに微分できるよ。こんな感じだね」
《簡単な関数を微分した例》
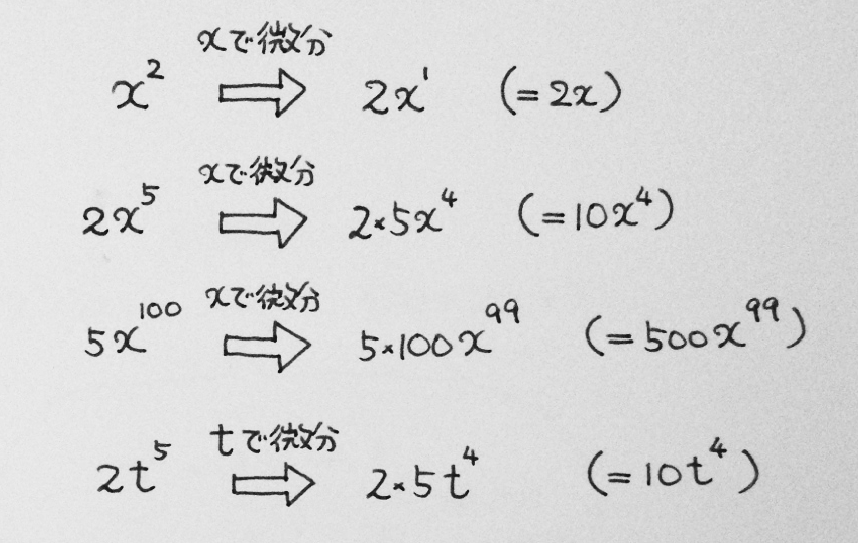
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年9月20日)
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!