![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/数列の広場』として書籍化されています。
ユーリ「また勝った。お兄ちゃん、意外と弱いよね」
僕「いや、ユーリが強すぎるんだよ」

ここは僕の自宅。 リビングで僕と従妹のユーリはオセロゲームをしていた。 ユーリがやたらと強いので僕は苦戦している。
ユーリ「苦戦しているって……四隅取られてるんだからボロ負けじゃん」
僕「そうとも言う」
ユーリ「弱い上に負けを認めないんだー、ふーん……」
僕「なお、オセロは登録商標です」
ユーリ「注意書きみたいなこと言ってないで、もっかいオセロやろーよー」
僕「もうオセロはいいよ。それより……」
ユーリ「お兄ちゃん、何やるの?」
僕はオセロの盤面から石をいったん片付けてから、 黒石を $1$ 個だけ角に置く。

ユーリ「何これ。ねーお兄ちゃん、いくら自分がカドを取れないからって、 最初からこれはないんじゃない? ルール違反!」
僕「いやいや。まあ、見ててよ。次はこうだよ」

ユーリ「んん? さっきの盤面の再現……でもないか。 何か新しいルールの研究?」
僕「どうかな、次はこう」

ユーリ「ははーん、わかったよ。角から順番に並べてるんだね!」
僕「そうだね」
ユーリ「あれだよね。黒が $1$ 個、それから白が $3$ 個、それから黒が $5$ 個……」
僕「この次はどうなると思う、ユーリ?」
ユーリ「こんなの簡単だよ、こーでしょ?」
ユーリはささっと白石を並べる。

僕「うん、そうだね。いまユーリが並べた白石は何個?」
ユーリ「白が $7$ 個だよん」
僕「規則性はわかる?」
ユーリ「わかるよ。 $1,3,5,7$ でしょ。もっと行くと $9,11,13,15$ 個並ぶ」
僕「$15$ 個の次は?」
ユーリ「そんなのひっかかんないよーだ! 次は $17$ 個だけど、オセロ盤からはみだしちゃうじゃん!」
僕「ひっかかんないか」

ユーリ「しまもようだね」
僕「ねえ、ユーリ、いまユーリが言ってくれた $1,3,5,7,9,11,13,15$ のことを何て言うか知ってる?」
ユーリ「ん? うん、知ってる。 $1,3,5,7,9,\ldots$ は、奇数でしょ?」
僕「そうだね。その通り。オセロ盤を越えて考えれば、 $15$ を越えてもずっと奇数はある。 奇数を並べた数列、奇数の列だ」
奇数の列
$$ 1,\,3,\,5,\,7,\,9,\,11,\,13,\,15,\,17,\,19,\,21,\,23,\,25,\,27,\,29,\,\ldots $$
ユーリ「すうれつ?」
僕「数を列にして並べたものが数列だよ。これは奇数を並べて作った数列」
ユーリ「ふーん。ねえ、お兄ちゃん。奇数の列って $1,3,5,7,9$ を繰り返してるね」
僕「あ、そうだね。一の位のことだね」
ユーリ「ところでその奇数の列がどうしたの? オセロもうやんないの?」
僕「さっきお兄ちゃんはこんなふうに石を並べたよね。 L字形にならべて、増やしていった」
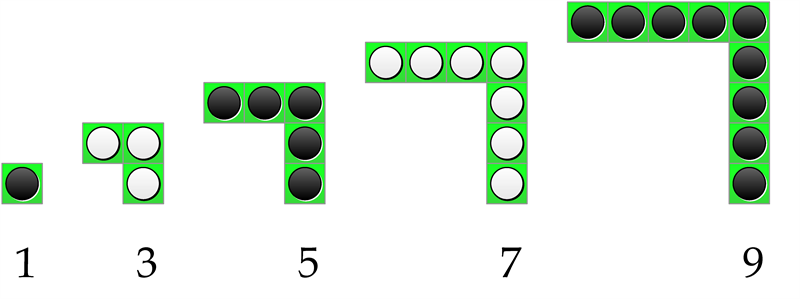
ユーリ「うん、そーだね。エル字っていうか、うえした逆だけど」
僕「そこでね、こんなふうに石のまとまりを見直してみよう」
僕は盤面の上に置かれた石に向かって、指で正方形を描く。

ユーリ「えっと、それは四角にまとめるってこと?」
僕「ただの四角じゃなくて、正方形だね。 辺の長さが全部等しくて、角の大きさがすべて等しい」
ユーリ「正方形……まー確かに、そーともゆー」
僕「そしてその正方形の中に何個の石があるかを数えてみよう」
ユーリ「ほーほー」
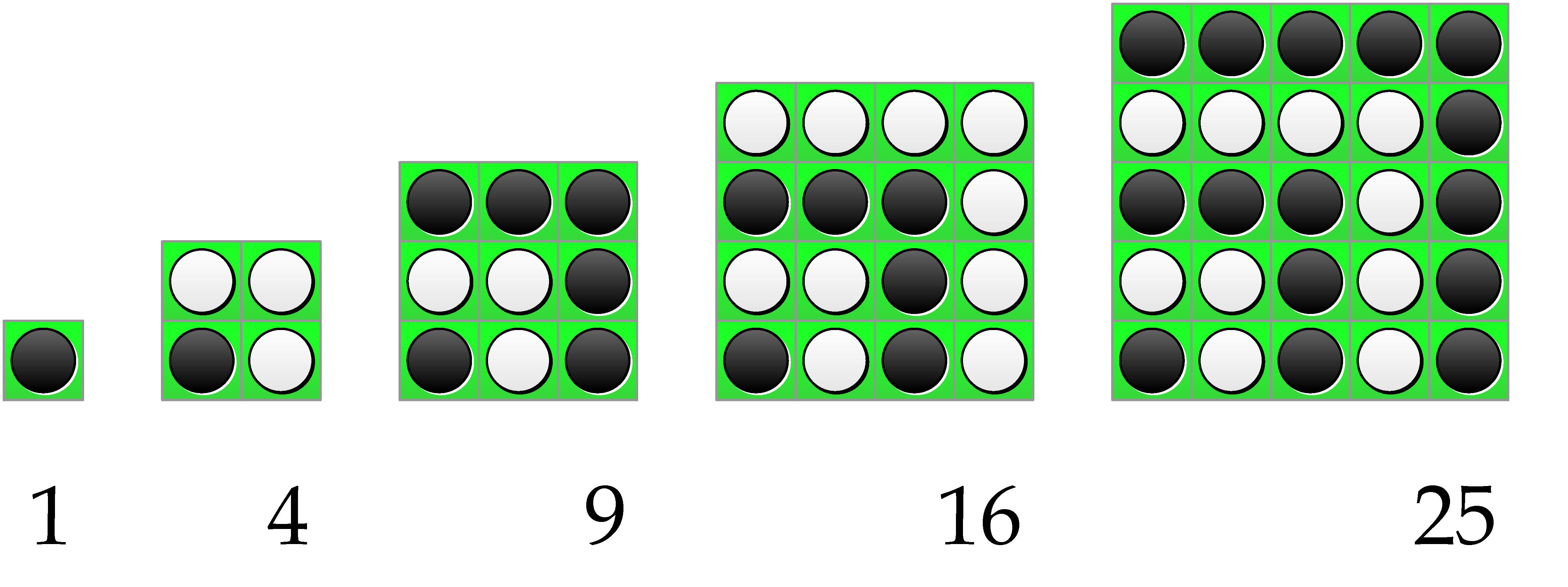
僕「今度はどんな規則性があるか、わかる?」
ユーリ「規則性って……見たらわかんじゃん! $1,4,9,16,25,\ldots$ って増えてく」
僕「そうだね。確かに見たらわかる。 でね、いまユーリが言った $1,4,9,16,25,\ldots$ というのは、平方数っていうんだ」
ユーリ「へいほーすう?」
僕「だから、 $1,4,9,16,25,\ldots$ は平方数の列といえる」
平方数の列
$$ 1,4,9,16,25,\ldots $$
僕「正方形の一辺の長さが $1,2,3,4,5,\ldots$ のように増えていくから、 正方形の中に置いた石の個数は $1 \times 1 = 1,$ $2 \times 2 = 4,$ $3 \times 3 = 9,$ $4 \times 4 = 16,$ $5 \times 5 = 25, \ldots$ のように増えていくんだね」
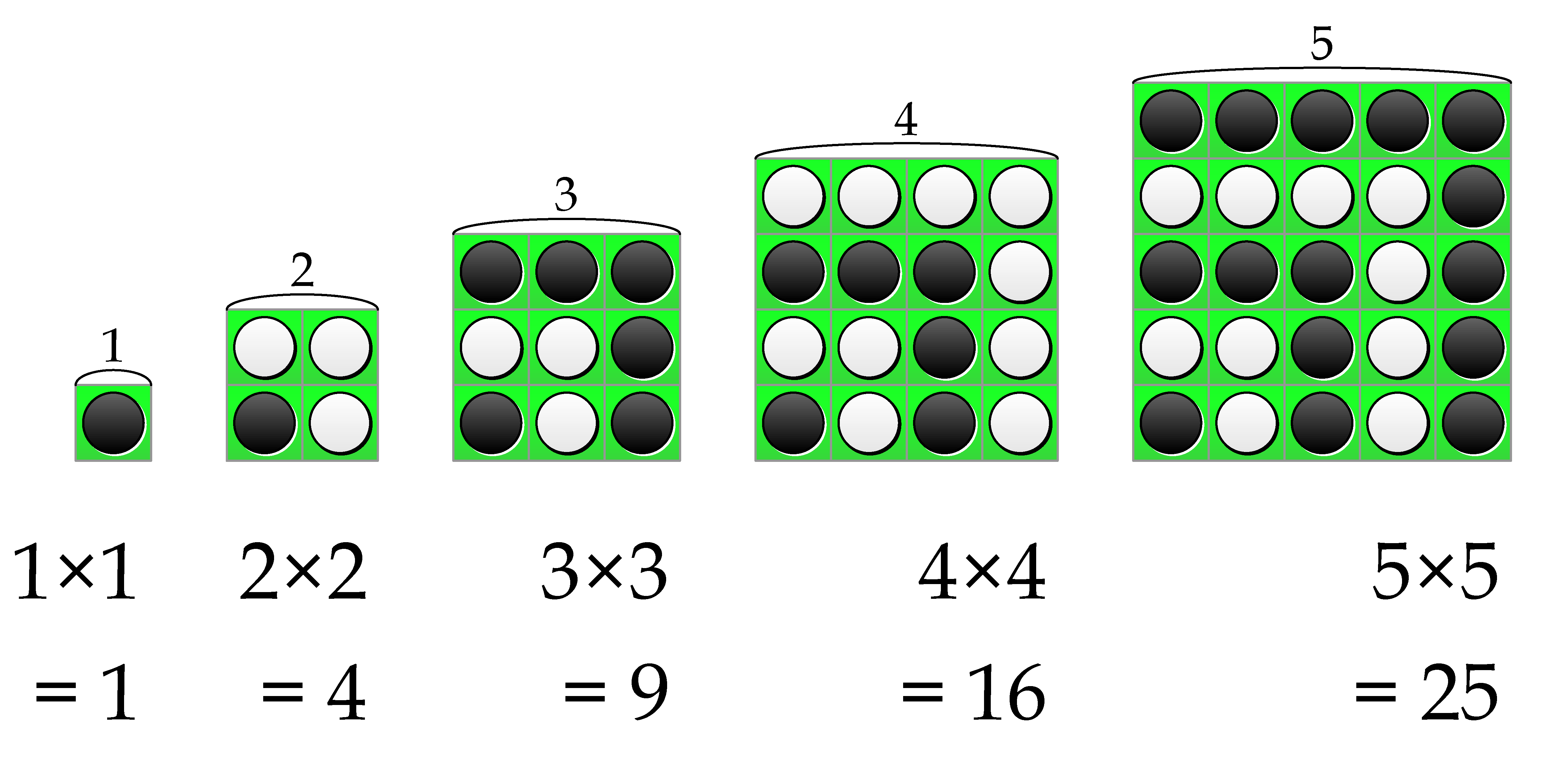
ユーリ「正方形……石 $1$ 個でも正方形?」
僕「そうだよ。縦が $1$ で横が $1$ の正方形。 $1 \times 1$ だね」
ユーリ「あそっか」
僕「ねえユーリ、オセロの盤で別のゲームをやってるみたいじゃない?」
ユーリ「えー、でも、別に勝ち負けないじゃん。石を並べるだけなら」
僕「まあそうか」
ユーリ「あ、ひらめいたよ!」
僕「何が?」
ユーリ「こーゆーの!」
ユーリ「ほらできたよ! うずまき!」

僕「え……うずまきなんて、どこにある?」
ユーリ「じっと見ると見えてくる……ここだよん!」

僕「ああ、ほんとだな」
ユーリ「はい、これで今回もユーリの勝ちだにゃ」
僕「いつから、勝ち負けがつくゲームやってたんだっけ?」
ユーリ「ねえ、お兄ちゃん」
僕「何?」
ユーリ「これって、きれいに並べたらいつも規則性が出てくるの? 奇数とか平方数とか……」
僕「ええとね……ねえ、ユーリ。 それは《きれいに並べる》っていう言葉の意味によるよね。 でも、まあ、普通は規則的に並べるときれいにみえるのは確かだね」
ユーリ「いまなにげに逆にしたね」
僕「え?」
ユーリ「ねーねー、もっと何かおもしろいことできないの? ねーねー」
僕「そうだなあ……だいたい、規則性があるところには数式が登場するんだよね」
ユーリ「でたな数式マニア。何でも数式で片付けられると思っているのかね?」
僕「急に上から目線だな。規則的なものは数式でとらえると楽しいんだよ」
ユーリ「たとえばたとえば?」
僕「たとえば、さっき作った正方形だけど」
ユーリ「あの $1 \times 1$ とか $2 \times 2$ とか?」
僕「そうそう。一辺の長さが石 $1$ 個分なら、正方形に並んだ石は $1 \times 1 = 1$ 個だね。 $1$ を $2$ 個掛けるから $1^2 = 1$ 個とも書く」
ユーリ「まーね。 $1^2$ なんて計算しなくてもわかるけどね。あたりまえだもん」
僕「あたりまえのときにも、きちんと式にしておくといいことがあるんだよ」
ユーリ「ふーん……それで?」
僕「一辺の長さが石 $2$ 個分なら、正方形に並んだ石は $2 \times 2 = 2^2 = 4$ 個ある」
ユーリ「で?」
僕「それじゃ、一辺の長さが石 $n$ 個分なら、正方形に並んだ石は何個?」
ユーリ「それは……それは、 $n \times n$ かにゃ? だから、 $n^2$ 個?」
僕「そうだね! それでいいよ。えらいえらい」
正方形に並んだ石の個数
一辺の長さが石 $n$ 個分なら、正方形に並んだ石は $n \times n = n^2$ 個ある。
ユーリ「それで? 別に楽しくもなんともないじゃん」
僕「じゃ、次はL字形の話だよ」
僕「さっき作ったL字形を覚えてるよね。一辺の長さが石 $1$ 個分なら、L字形に並んだ石は $1$ 個だった」
ユーリ「石 $1$ 個だとL字形じゃないけどねー」
僕「一辺の長さが石 $2$ 個分なら、L字形に並んだ石は $3$ 個だった」
ユーリ「うん、奇数になるんでしょ? $1, 3, 5, 7, 9, \ldots$」

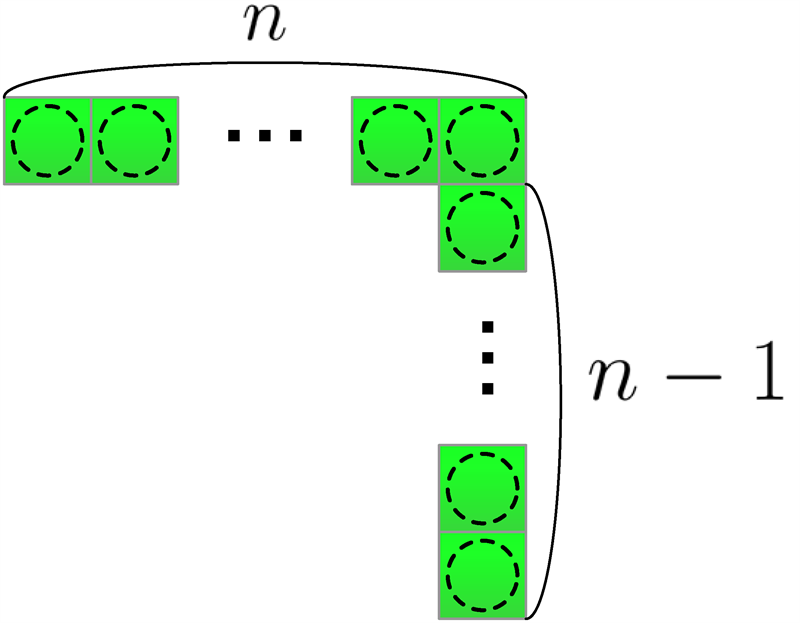
僕「それじゃね、一辺の長さが石 $n$ 個分あったら、L字形に並んだ石は何個?
クイズ
一辺の長さが石 $n$ 個分のとき、L字形に並んだ石は何個?
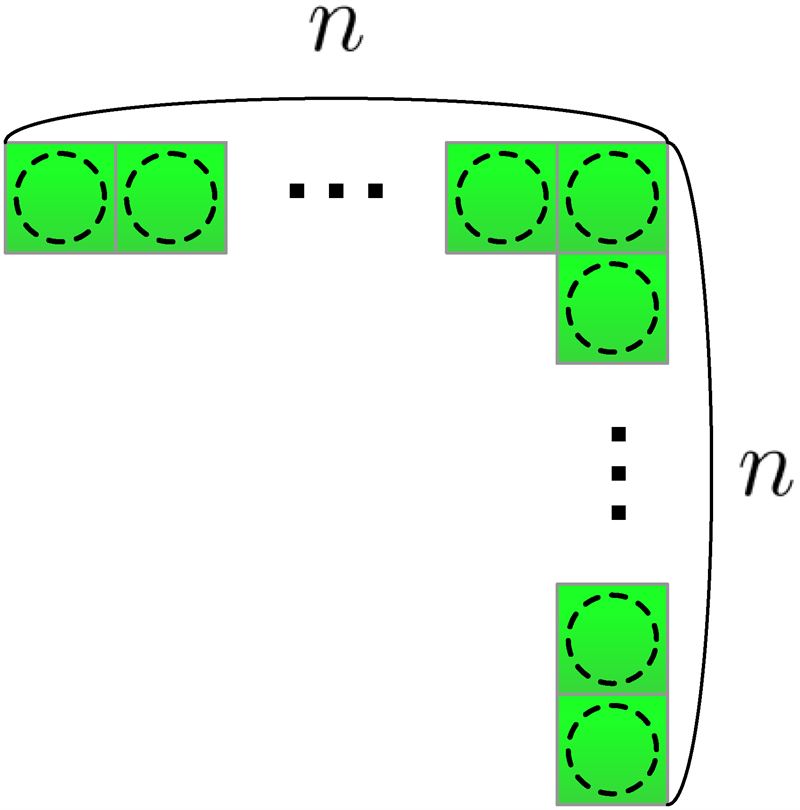
ユーリ「この点線の丸印はなに?」
僕「黒石か白石かわからないからね。 $n$ が奇数なら黒石だし、偶数なら白石になる」
ユーリ「うわ細かい話!」
僕「そんなことより、L字形に何個並んでる?」
ユーリ「簡単じゃん。 $n$ を……あれ?」
ユーリは栗色のポニーテールを揺らしながら考える。 天井を見上げ、指を折ってから答えた。
ユーリ「うん! L字形の石は $2n - 1$ 個だね!」
僕「えらいえらい、その通りだよ」
ユーリ「お兄ちゃん、ユーリのこと馬鹿にしてない?」
僕「してないよ。一辺が石 $n$ 個分のとき、L字形に並んだ石は $2n - 1$ 個で正しいよ。 こんなふうに横に $n$ 個、縦に $n-1$ 個あると考えれば、合計は $2n - 1$ 個だね」
クイズの答え
一辺の長さが石 $n$ 個分のとき、L字形に並んだ石は $2n - 1$ 個になる。
ユーリ「ちょっと心配になったのはね、 $2n - 1$ って式に、マイナス $1$ が出てきたからなんだよ。あれ、マイナス? って気になったの」
僕「うん、そうだと思ったよ。だから $n = 1$ のときにちゃんと $1$ になるか、 $n = 2$ のときにちゃんと $3$ になるか、 暗算で確かめてたんだろ?」
ユーリ「うっそ、なんでわかんの? テレパシー?」
僕「わかるんだよ」
ユーリ「へー」
僕「ところでね、これで僕たちは《正方形》と《L字形》について、一辺が $n$ のときの石の数がわかったよね」
ユーリ「え……あ、そだね」
一辺が $n$ のときの石の数
$$ \begin{align*} \REMTEXT{正方形の石の数} &= n^2 \\ \REMTEXT{L字形の石の数} &= 2n - 1 \\ \end{align*} $$
僕「それから僕たちは、L字形を小さい方から順番に重ねていって正方形が作れることを知っている。 たとえばL字形を $8$ 個重ねるとオセロ盤ができる」

ユーリ「ふむふむ?」
僕「この重ね方をじっと見ると、次の数式が見えてくる」
$$ 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 8^2 $$ユーリ「うん?」
僕「左辺の $1 + 3 + 5 + 7 + 9 + 11 + 13 + 15$ は何だかわかる?」
ユーリ「えっと……奇数を足してる。 $1$ から $15$ まで——あ! L字形の石の数を足してるんだね。 $1,3,5,7,9,11,13,15$ を足していってるんだ」
僕「そうだね。じゃあ右辺の $8^2$ は?」
ユーリ「オセロ盤全体でしょ? オセロ盤全体の石の数」
僕「そうそう!」
$$ 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 8^2 $$ユーリ「これが、おもしろいこと? あたりまえのことじゃん!」
僕「ここから僕たちは一般化ができるんだよ。 $n$ という文字を導入した《文字の導入による一般化》だ」
ユーリ「む? どゆこと?」
僕「オセロ盤を使っているから $15$ までで止めたけど、これはずっと続けることができる。 このことは $n$ という文字を使うと表現できるんだ」
ユーリ「何言ってるかわかんない」
僕「こういうことだよ。こういう式が成り立つことがいえるんだ」
$$ 1 + 3 + 5 + \cdots + (2n - 1) = n^2 $$ユーリ「?」
僕「$1$ から順に奇数だけを足していくんだけど《$15$ まで》という具体的な数じゃなくて、 《$2n - 1$ まで》足したんだよ。途中を省略しているのでテンテン($\cdots$)を使っているよね」
ユーリ「あ、わかったよ」
僕「そして右辺はその結果として、大きな正方形ができる。その石の個数は、 もちろんL字形を足し合わせたものに等しいはずだから、 $n^2$ 個になる」
ユーリ「ほほー」
僕「言葉で言えばこういうことだよ。 《$1$ から始めて $n$ 個の奇数を足した数》は《平方数 $n^2$》に等しい」
《$1$ から始めて $n$ 個の奇数を足した数》は《平方数 $n^2$》に等しい
$$ 1 + 3 + 5 + \cdots + (2n - 1) = n^2 $$
ユーリ「あれ? $n$ 個の奇数なの? $2n - 1$ 個の奇数じゃないの?」
僕「いやいや、違うよ。 $2n - 1$ というのはいま足した中でいちばん大きい奇数《そのもの》のこと。 お兄ちゃんが言った $n$ 個の奇数っていうのは足し合わせた奇数の《個数》のこと」
ユーリ「んんんん?」
僕「具体的に見ればすぐわかるよ。 $1 + 3 + 5 + \cdots + (2n - 1) = n^2$ の $n$ を $1$ から順番に増やしてみるよ」
$$ \begin{array}{rcll} \underbrace{1}_{\REMTEXT{$1$個}} &=& 1^2 & \REMTEXT{$n = 1$のとき} \\ \underbrace{1 + 3}_{\REMTEXT{$2$個}} &=& 2^2 & \REMTEXT{$n = 2$のとき} \\ \underbrace{1 + 3 + 5}_{\REMTEXT{$3$個}} &=& 3^2 & \REMTEXT{$n = 3$のとき} \\ \underbrace{1 + 3 + 5 + 7}_{\REMTEXT{$4$個}} &=& 4^2 & \REMTEXT{$n = 4$のとき} \\ \underbrace{1 + 3 + 5 + 7 + 9}_{\REMTEXT{$5$個}} &=& 5^2 & \REMTEXT{$n = 5$のとき} \\ \underbrace{1 + 3 + 5 + 7 + 9 + 11}_{\REMTEXT{$6$個}} &=& 6^2 & \REMTEXT{$n = 6$のとき} \\ \underbrace{1 + 3 + 5 + 7 + 9 + 11 + 13}_{\REMTEXT{$7$個}} &=& 7^2 & \REMTEXT{$n = 7$のとき} \\ \underbrace{1 + 3 + 5 + 7 + 9 + 11 + 13 + 15}_{\REMTEXT{$8$個}} &=& 8^2 & \REMTEXT{$n = 8$のとき} \\ \underbrace{1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17}_{\REMTEXT{$9$個}} &=& 9^2 & \REMTEXT{$n = 9$のとき} \\ \underbrace{1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19}_{\REMTEXT{$10$個}} &=& 10^2 & \REMTEXT{$n = 10$のとき} \\ &\vdots& \\ \underbrace{1 + 3 + 5 + \cdots + (2n - 1)}_{\REMTEXT{$n$個}} &=& n^2 & \REMTEXT{一般形} \\ \end{array} $$ユーリは僕が書いた式を長いこと見つめていた。
ユーリ「……わかった。わかったよ、お兄ちゃん。おもしろいね。 $1$ から奇数を $n$ 個足すとき、最後の奇数は $2n - 1$ になるんだね」
僕「そうそう!」
僕「よくじっくり数式を読んだね。えらいなあ」
ユーリ「お兄ちゃんがたくさん書いてくれたから、 $n$ が何なのかわかったよ。 ねー……あのね、 $n$ とか $x$ とか、何でもいいけど文字が出てくるとね」
僕「うん」
ユーリ「難しくはないんだけど、なんだか難しい」
僕「なんだそりゃ」
ユーリ「そーゆー感じなの! ……難しくはないんだけど、ちょっと《あれれ?》って思うんだよ」
僕「ああ、そうかもね」
ユーリ「でも、文字が出てきても実際の数を入れて考えればバシっとわかるんだね」
僕「そうだね。ユーリはよくわかっているな。すごくえらいぞ!」
ユーリ「……ねえ、お兄ちゃん」
僕「なに?」
ユーリ「あのね……」
僕「なんだよ」
ユーリ「あのね、お兄ちゃんってね、ユーリのこと、よくホメてくれるよね。《えらい》って」
僕「ん? そう? まあ、そうかもね」
ユーリ「あのね……ちょっと恥ずかしいけど、ホメられるのって、うれしーね」
僕「それはよかった」
ユーリ「《それはよかった》……だけ?」
僕「え?」
ユーリ「まーいいや。さて休憩も済んだし、もっかいオセロやろうよ。一辺が $n = 8$ の場合のオセロゲーム」
僕「一辺が $n = 1$ だったらやってもいいな」
ユーリ「へ?」
僕「先手必勝のオセロゲーム!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 430本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第31回終わり)
(2013年5月31日)
この記事は『数学ガールの秘密ノート/数列の広場』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!