第21回 シーズン3 エピソード1

まるい三角形（前編） ただいま無料

図書室にて

僕「テトラちゃん、今日も数学？」

テトラ「あ、先輩！　はい、そうです。先輩にいろいろ教えていただくので、 数学を勉強するのがとても楽しくて……」

僕「それは良かった。最近は何をしているのかな」

テトラ「はい……最近取り組んでいるのは三角関数です」

僕は数学が好きだし、得意だ。一人で勉強するときも、まずは数学から始める。 テトラちゃんは数学が苦手だったけれど、僕と話すようになってから急に好きになったようだ。

僕「なるほど。 $\sin$ （サイン）や $\cos$ （コサイン）だね」

テトラ「はい……」

ところがテトラちゃんは顔を急に曇らせた。

僕「どうしたの？」

テトラ「は、はい。先輩から数学のお話をお聞きするのは楽しいんですが……三角関数はとても難しいです」

僕「ああ、そうかもしれないね。慣れてしまえばそれほどじゃないんだけど」

テトラ「三角関数っていうから、図形の話かと思ったらそうでもなくて、公式がたくさん出てきますよね。 たくさん覚えることもあって、でも、なんだかよく《わかった感じ》がしないんです」

僕「確かにそうだね。三角関数は公式がたくさんある」

テトラ「暗記するのはそんなにきらいではないんですが……何をやっているのかさっぱりわからないんです。 三角関数って、何なんでしょうか？」

僕「それにひとことで答えるのは難しいなあ。うん、でも、いっしょに考えてみようか」

テトラ「はい、よろしくお願いしますっ！」

直角三角形

僕「テトラちゃんがどこまでわかっているかわからないから、すごく基本的なところから話してもいい？」

テトラ「はいはい、もちろんです」

僕「じゃあ、まず、直角三角形を描いてみて」

テトラ「はい……こうでしょうか」

僕「うん、確かにこれは直角三角形に見えるね」

テトラ「はい……え、な、何か変ですか？」

僕「直角三角形を描いたら『ここが直角ですよ』と《直角の印》を明記した方がいいよね」

テトラ「あっと、そうですね。《ここが直角ですよ》…と」

素直なテトラちゃんはすぐに、僕のいった通り《直角の印》を描いた。

直角三角形は、どこが直角かわかるように《直角の印》を明記する

僕「そうそう、そういうこと。こういうのは細かいことだけど、主張がわかりやすくなるし、それに自分が考えるときのヒントにもなるんだよ」

テトラ「はいっ、わかりました」

テトラちゃんは元気に返事をして、いつもの《秘密ノート》にメモをする。

角の名前

僕「まずは当たり前のことから。三角形には三つの角があって、 直角三角形はそのうちの一つの角が直角——つまり $90$ 度になっているよね」

テトラ「はい、そうですね。一つの角が直角」

僕「それで、残りの二つの角のうち、片方に注目する。 その角に $\theta$（シータ）と名前をつけておこう」

テトラ「シータ……ですね。あ、先輩、これはギリシア文字ですよね」

一つの角に $\theta$ と名前をつける

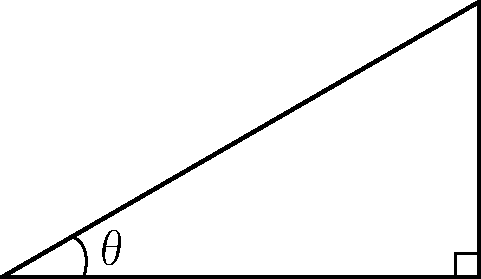
僕「うん、そうだね。名前は何でもいいんだけれど、角はギリシア文字で表すことが多いよ」

テトラ「わかりました」

僕「数学だといろんな文字や記号や名前が出てくるし、それでめげてしまう人もいる」

テトラ「あ……実はあたしも、たくさんの文字が出てくるのは苦手です。 いつも《待って待って》って言いたくなっちゃうんです。 ぜんぶをつかまえる前に逃げてしまいそうで」

僕「そうなんだ。でも数学の文字は逃げたりしないから大丈夫だよ」

テトラ「そうですよね……」

僕「もしもね、勉強しているときにたくさんの文字が出てきて嫌になりそうだったら、 《ゆっくり進む》ようにしたほうがいいよ。つまりね、文字に慣れるまで先を急がないこと」

テトラ「あ、なるほど。それは良さそうです！　あたし、ひとつひとつの文字と《お友達》になれるようにします」

頂点と辺の名前

僕「名前の話が出たから、ついでに頂点と辺の話もしておくよ。 テトラちゃんが描いてくれた三角形の頂点と辺に名前をつけてみよう。 三角形 $ABC$ だ」

三角形 $ABC$

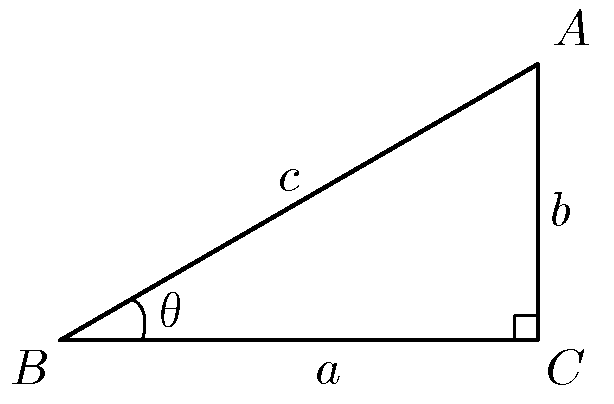
テトラ「$A$ と $B$ と $C$ が頂点（ちょうてん）ですね」

僕「そうだね。頂点は大文字のアルファベットで書くことが多いね。 そして三つの頂点を順番に並べて三角形を表す。 $A$ → $B$ → $C$ でぐるっと回って三角形だね」

テトラ「はい、よくわかります。三角形 $ABC$ ですね」

僕「そうそう。図形についての文章を読むとき、文字が出てきたら必ず図と照らし合わせて読むことが大事」

テトラ「照らし合わせるってどういう意味ですか」

僕「三角形 $ABC$ だったら……図で頂点 $A$ と頂点 $B$ と頂点 $C$ がどこにあるかを確認するということだよ」

テトラ「わかりました。 $A$ はここ、 $B$ はここ、 $C$ はここにありますっ」

テトラちゃんは元気に頂点を《指さし確認》した。

僕「頂点と辺の名前の付け方は少し違う。 頂点は大文字のアルファベットで書くのに対して、辺は小文字のアルファベットを使うことが多い。 辺の名前は、その辺と向かい合った頂点と同じアルファベットを使って、大文字小文字だけを変える」

テトラ「こういうことですね。頂点 $A$ と辺 $a$ ……」

頂点（大文字）と同じアルファベットを、向かい合った辺の名前（小文字）に使う

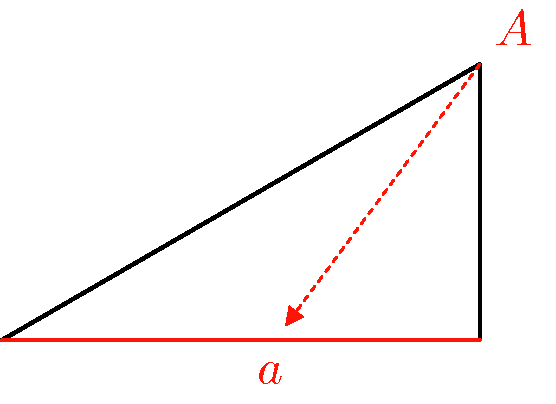
僕「そうだね。頂点 $B$ と辺 $b$」

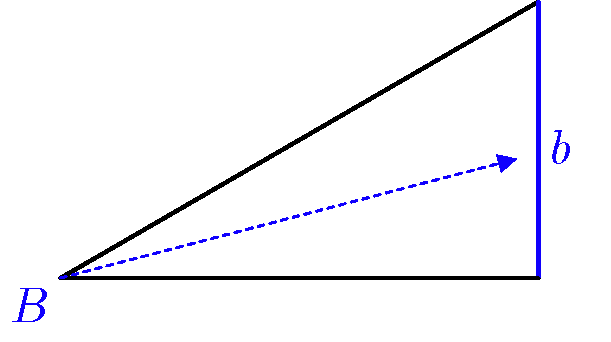
テトラ「そして、頂点 $C$ と辺 $c$ ですね」

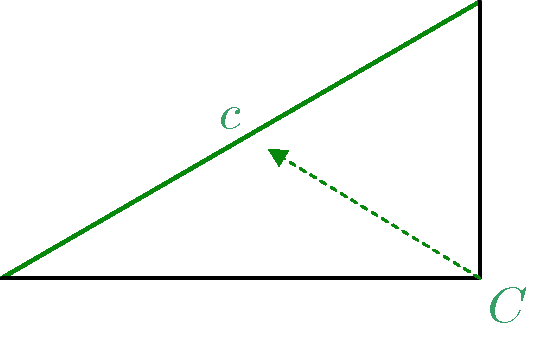
僕「これは《絶対こうしなくちゃいけない》というわけじゃないよ。 まったく違う文字の使い方をしても、数学的にはかまわない。 ただ、多くの場合はこうしているという慣習の問題だね」

テトラ「はい、よくわかります」

サインの話

僕「さてと。いま直角三角形で、角 $\theta$ と、二辺 $b$ と $c$ に注目しよう。この図をよく見る」

テトラ「はい」

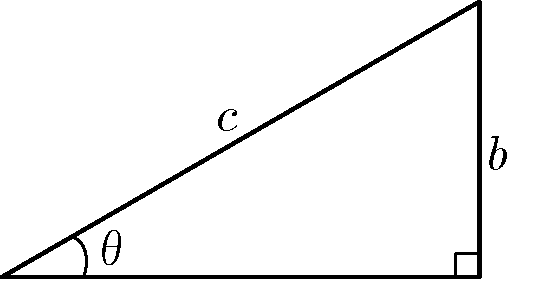
素直なテトラちゃんは図をじっと見つめる。 いや、見つめるだけじゃない。 （辺 $b$ と辺 $c$）とつぶやきながら指さし確認している……ほんとに素直だなあ。

僕「これから、《角 $\theta$ の大きさ》と《二辺 $b$ と $c$ の長さ》の関係について考えたい」

テトラ「角と辺……」

僕「直角三角形で、いま注目している《角 $\theta$ の大きさ》を変えないように注意して、 《辺 $c$》をするする伸ばしてみよう。 たとえば、辺 $c$ の長さを $2$ 倍に伸ばしたとする。すると、僕たちの直角三角形はこうなる」

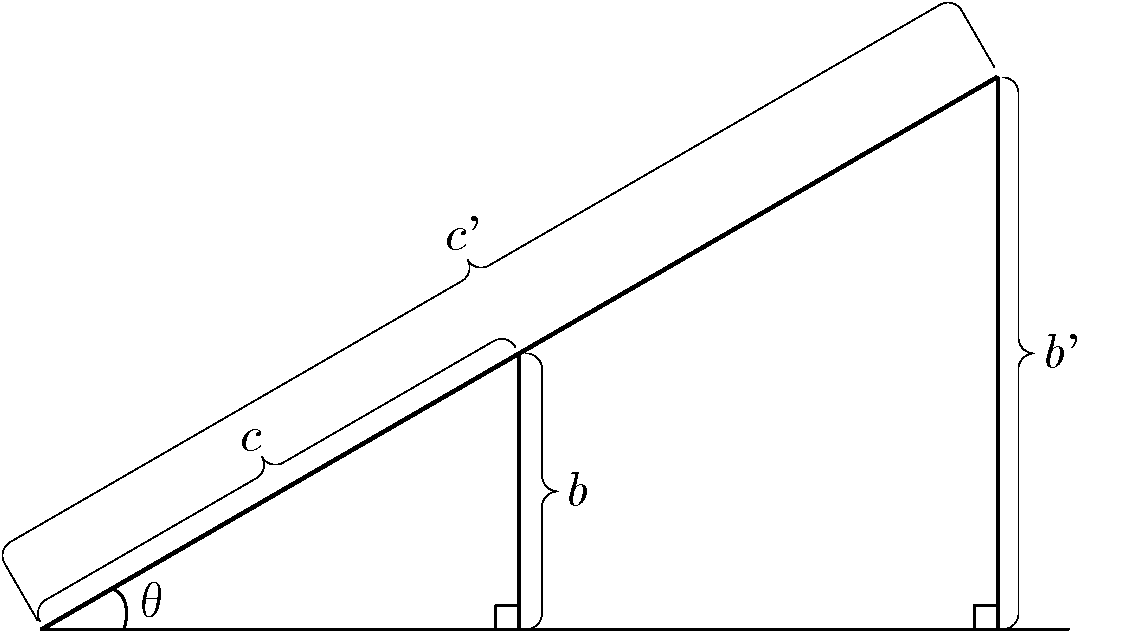
テトラ「はい……これは、辺 $c$ が辺 $c^{\prime }$ まで伸びたということですね」

僕「そうだよ。直角三角形にするためには縦の辺 $b$ は辺 $b^{\prime }$ にならなくちゃまずいよね」

テトラ「はい、わかります」

僕「辺 $c$ を辺 $c^{\prime }$ にして、長さが $2$ 倍になったとすると、 辺 $b$ は辺 $b^{\prime }$ になって、こちらも長さは $2$ 倍になるよね」

テトラ「ええと……あ、そうですね」

僕「$2$ 倍に限らず、辺 $c$ を $3$ 倍、 $4$ 倍、……にすれば、 辺 $b$ も $3$ 倍、 $4$ 倍、……になる」

テトラ「はい。比例します」

僕「そう！　つまりね《角 $\theta$ の大きさが一定》なら《辺 $b$ と辺 $c$ の比（ひ）も一定》になる」

テトラ「比も一定……」

僕「言い換えると、《角 $\theta$ の大きさが一定》なら《分数 ${\displaystyle \frac{b}{c}}$ の値は一定》ということ」

テトラ「先輩、それは分子 $b$ を $2$ 倍、 $3$ 倍……にするとき、分母 $c$ も $2$ 倍、 $3$ 倍……になるということを おっしゃっているのですよね？」

僕「そうだよ」

テトラ「はい、納得です！　……先輩、すみませんけど」

僕「なに？」

テトラ「これは、三角関数に関係しているんですか？」

僕「うん、関係しているよ。もう少しで出てくる……というか、もう出てきている」

テトラ「はい？」

僕「いま僕たちは、こういうことを考えたね」

テトラ「そうですね」

僕「こんなふうに言ってもいい」

テトラ「はい、それはそうですね。 だって、角 $\theta$ を決めてしまえば——直角三角形の形を保っている限り——分数 ${\displaystyle \frac{b}{c}}$ の値も決まります。 実際にどうやって求めるかはわかりませんけれど、決まるのは確かです」

僕「それが $\sin$ なんだよ、テトラちゃん」

テトラ「え？」

僕「《角 $\theta$ の大きさ》を決めたら《分数 ${\displaystyle \frac{b}{c}}$ の値》も決まる。 つまり、《分数 ${\displaystyle \frac{b}{c}}$ の値》は $\theta$ で決まる。 だから、その《分数 ${\displaystyle \frac{b}{c}}$ の値》に名前をつけてあげよう。 それを $\sin \theta$ と呼ぶことにしよう！」

テトラ「……！」

僕「こんなふうに、直角三角形で説明するのはとても手軽な説明だけど……うわっ！」

テトラちゃんが急に僕の腕をつかんできた。

テトラ「先輩、先輩、先輩！　三角関数のサインってそれだけのことなんですか？」

僕「それだけのこと？」

テトラ「$\sin \theta$ は……直角三角形の ${\displaystyle \frac{b}{c}}$ の値なんですか！？」

僕「そうだよ。それでいい。直角三角形だから $\theta$ の範囲は $0^{\circ }<\theta <{90}^{\circ }$ だけどね」

テトラちゃんは「うわっ、うわっ」などといいながら《秘密ノート》にメモをしている。

サインの覚え方

テトラ「……これ、授業で習っていたはずですよね」

僕「そうだね。三角比（さんかくひ）という授業で習うと思うよ」

テトラ「その授業、たくさんの文字で圧倒されていたような気がします」

僕「そう？　まだそんなにたくさん文字は出てきてないけどね」

テトラ「いえいえ、三角形には辺が $3$ 本あって、分母と分子にどれを持ってくるのかで、全部で何通りもあるじゃないですか！」

僕「ああ、覚え方の話？　 $\sin$ の覚え方として有名なのはこれだよね。筆記体のsを使って《$c$ 分の $b$》という順に分数を作る。 sは $\sin$ のsだよ」

$\sin \theta$ の覚え方

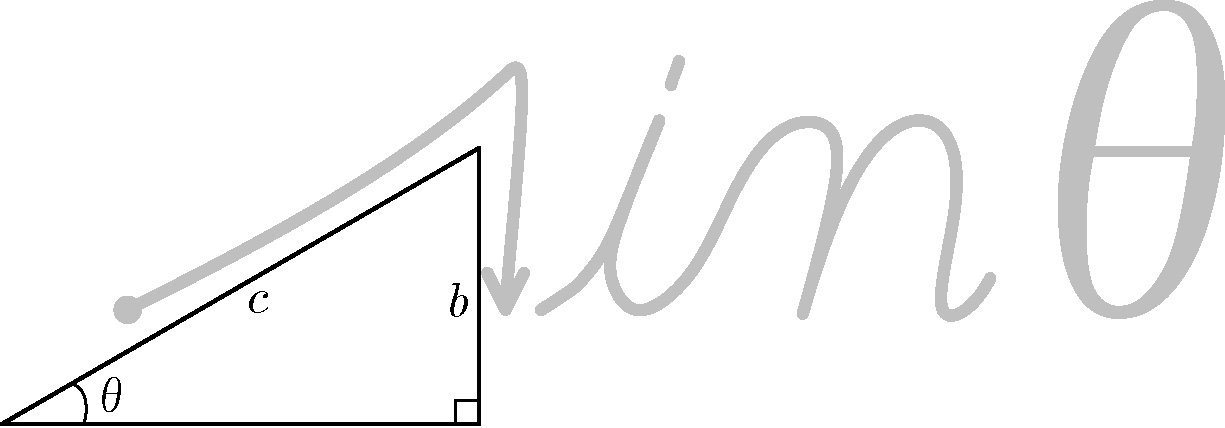
テトラ「はい……そういえば、これも習ったのを思い出しました。 でも、今度は三角形の置き方で迷ったんです。直角をどこに置くのかしら……って」

僕「ははは、なるほど。三角形の置き方で迷うわけだ。 この覚え方は《直角をどこに置くか》と考えるんじゃないよ。 この覚え方は《注目している角 $\theta$ を左に置く》って考えるんだ」

テトラ「$\theta$ を左に置く……」

僕「そう。さっき話したように、 $\theta$ が決まれば ${\displaystyle \frac{b}{c}}$ が決まる。 だから、 $\theta$ をしっかり押さえておく」

テトラ「……」

僕「つまり《$\sin$ は、 $\theta$ から ${\displaystyle \frac{b}{c}}$ を求める関数》といえるんだね」

テトラ「……！」

コサインの話

僕「$\sin$ がよくわかったら、 $\cos$ もすぐにわかるよ。 直角三角形で、角 $\theta$ と、二辺 $a$ と $c$ に注目する。 注目する辺がさっきと違う」

テトラ「はい」

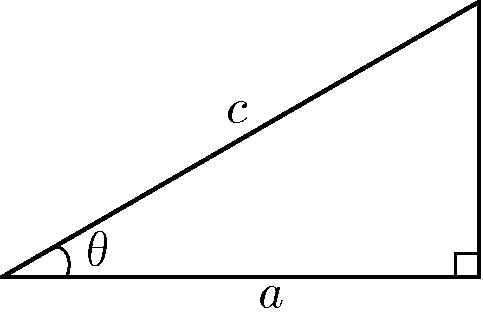
僕「さっきと同じように《角 $\theta$ の大きさ》を変えないように注意して、 《辺 $c$》をするする伸ばしてみよう。 たとえば、辺 $c$ の長さを $2$ 倍に伸ばしたとする。すると、僕たちの直角三角形はこうなる」

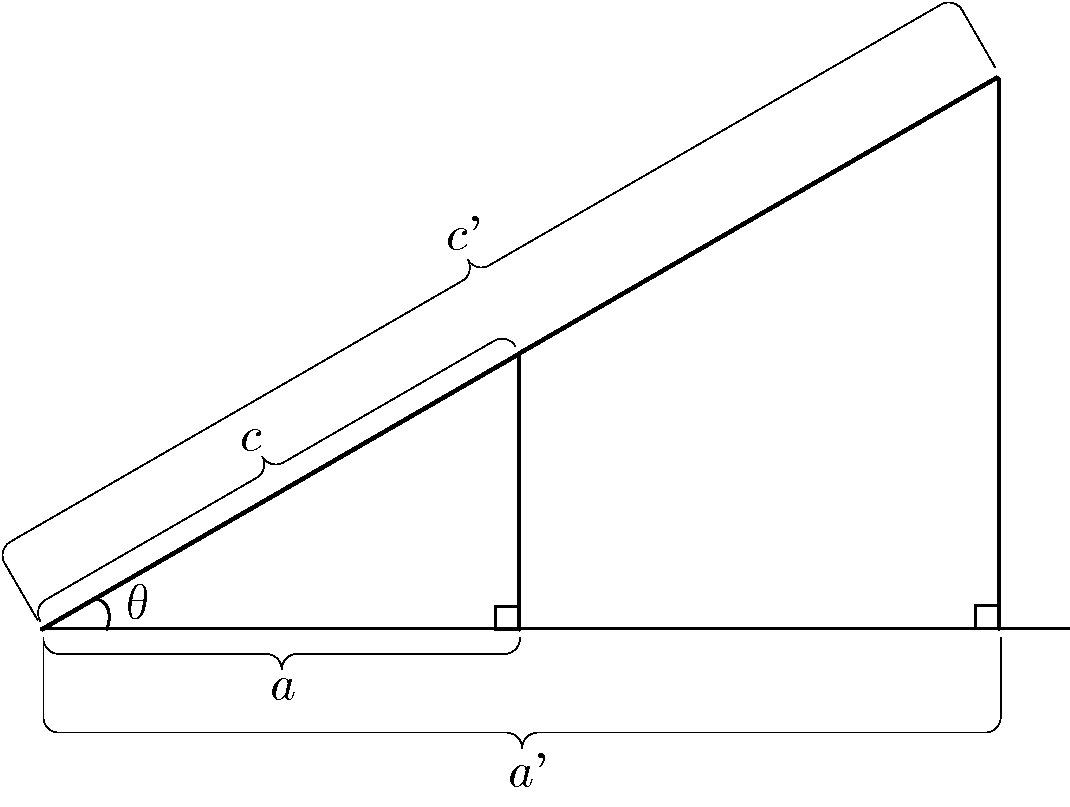
テトラ「あ……今度は横の辺 $a$ が $2$ 倍の長さの $a^{\prime }$ に……？」

僕「そうなるね。今度は《角 $\theta$ の大きさが一定》なら《辺 $a$ と辺 $c$ の比（ひ）も一定》というところに注目する。それが $\cos$ だ」

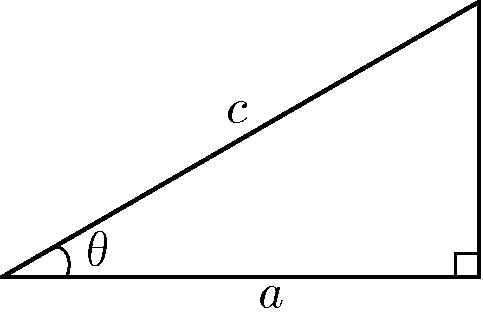
テトラ「さっきとそっくりですね……」

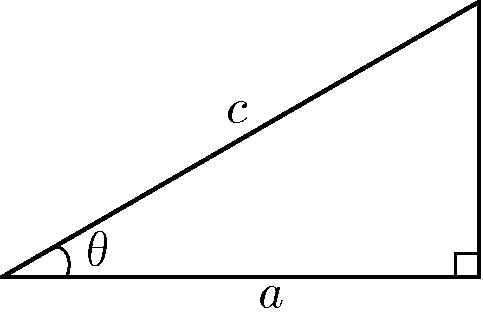
僕「$\cos$ を覚えたいときは、今度はcという文字の形を使う。cは $\cos$ のcだよ」

$\cos \theta$ の覚え方

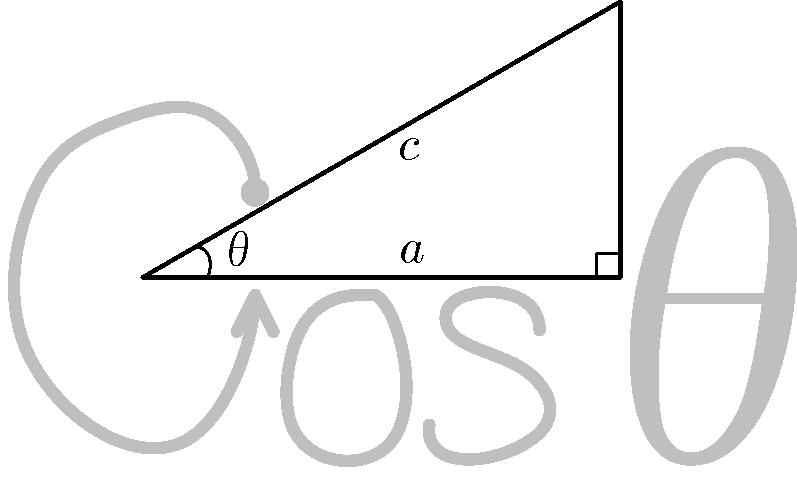
テトラ「あ、こちらの方も《注目している角 $\theta$ を左に置く》ようになってますね」

僕「そうだね。以上が $\sin$ と $\cos$ の基本になる」

テトラ「ここまで、よくわかりましたっ！」

僕「そして、次にやることは $0^{\circ }<\theta <{90}^{\circ }$ の制限を外すことだ」

テトラ「制限を……外す？」