第398回 シーズン40 エピソード8

素数を法とする世界（後編）

図書室にて

テトラ「……なるほど。逆を考えるということ、気付きませんでした。 つまり、これが証明できたことになるんですね！」

僕「うん、そうだね。 だから、

• $P(n)$ を「$n$ は素数である」
• $Q(n)$ を「$0 < r < n$ を満たす任意の整数 $r$ について $\BINOM{n}{r}$ は $n$ の倍数である」

テトラ「それにしても、パスカルの三角形は奥が深いです。 簡単に作っていくことができるのに、そこにさまざまな数のパターンが出てきます。 それから、組み合わせの数のようにおもしろい性質を持つものも出てきますし……」

僕「うん、そうだよね。パスカルの三角形は具体的に《小さな $n$ で試す》ことができるのも楽しい」

テトラ「あっ、それ思いました。先輩の証明でも、 まず、小さな $n$ でたくさん試していましたよね。 あたし、とても参考になって——そして、すごく反省しました……」

僕「えっ、どうして？」

テトラ「あたしは、文字がたくさん出てくるのが苦手なくせに、 つい、一気に文字を使った証明を書こうとしちゃうんです……そして失敗する」

僕「そうかなあ。テトラちゃんこそ、 根気よくたくさんの数で試す印象があるんだけど」

テトラ「ええとですね……確かにあたしは根気よくやればわかるかも！——と思いがちです。 でも、違うんですよ。あたしが思うに、根気よくやるだけじゃ駄目なんです」

僕「うーん……《小さな $n$ で試す》ときは、焦らないで根気よくやる必要があるよね。 根気よく、ていねいに進んで、よく観察しないと一般的な性質を見つけることはむずかしいから」

テトラ「そこっ！　そこです。 根気よくやるだけじゃ駄目で、ていねいに進む。 ただ進むだけじゃ駄目で、よく観察する。 それが必要になると思うんです。 あたしはどうしても、バタバタッと進んでしまい、とにかく数をこなそうとしちゃうみたいで……だから、 先輩の《小さな $n$ で試す》お話はとても参考になりました。 素数がどこに出てくるかを注意深く観察なさっていましたし（第397回参照）」

僕「なるほどね。うん、でも、今回の証明の場合には素因数分解が直接的に登場したからわかりやすかったよ。 《整数の構造は、素因数が示す》からね」

【ＣＭ】

ユーリ「《整数の構造は、素因数が示す》——お兄ちゃんの名言キタ！　 くわしくは『数学ガール／フェルマーの最終定理』を読んでね！」

二項係数

テトラ「ところで先輩。組み合わせの数 $\BINOM{n}{r}$ は二項係数（にこうけいすう）と同じですよね？」

僕「うん、そうだよ。どうして $\BINOM{n}{r}$ を二項係数というかというと——」

テトラ「ちょ、ちょっとお待ちください。あたしに言わせてください。 これは先輩に何度も教えていただきましたから、あたしも説明できるはずです」

僕「ごめんごめん。テトラちゃん、どうぞ！」

テトラ「二項係数は、 $x + y$ のように二つの項がある式を $n$ 乗したとき、つまり、 $$ (x + y)^n $$ を展開したときに出てくる係数になっています。 《小さな $n$ で試す》ことをやってみます」

僕「うん、いいね！」

$n = 2$ の場合

テトラ「$n = 2$ の場合 $(x+y)^n= (x+y)^2$ で、展開するとこうなります」

僕「係数の列 $1,2,1$ を明示的に書くのはわかりやすいよね」

テトラ「はい——これも先輩がこう書いているのを見て真似してるんですが——ともかくこれで、 $n = 2$ の場合に、係数が $1,2,1$ となるのがわかりました。 パスカルの三角形の $2$ 行目の数です」

僕「そうだね」

テトラ「ところでこの途中に出てきた $$ xx + xy + yx + yy $$ の式をよく観察すると、 $x$ と $y$ という $2$ 種類の文字から $2$ 文字を選んで並べるすべての順列が出てきます」

僕「うんうん！」

テトラ「これは、 $n = 3$ でも同じことが起きます」

僕「てきぱき進むねえ！」

$n = 3$ の場合

テトラ「$n = 3$ の場合 $(x+y)^n= (x+y)^3$ で、 あたしは $1,3,3,1$ と係数を暗記していますけれど、あえて展開するとこうなります」

僕「いいねえ」

テトラ「いま出てきた、 $$ xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy $$ には、 $x$ と $y$ という $2$ 種類の文字から $3$ 文字を選んで並べるすべての順列が出てきます」

僕「うん。それは——」

テトラ「これは、こんなふうにイメージできます」

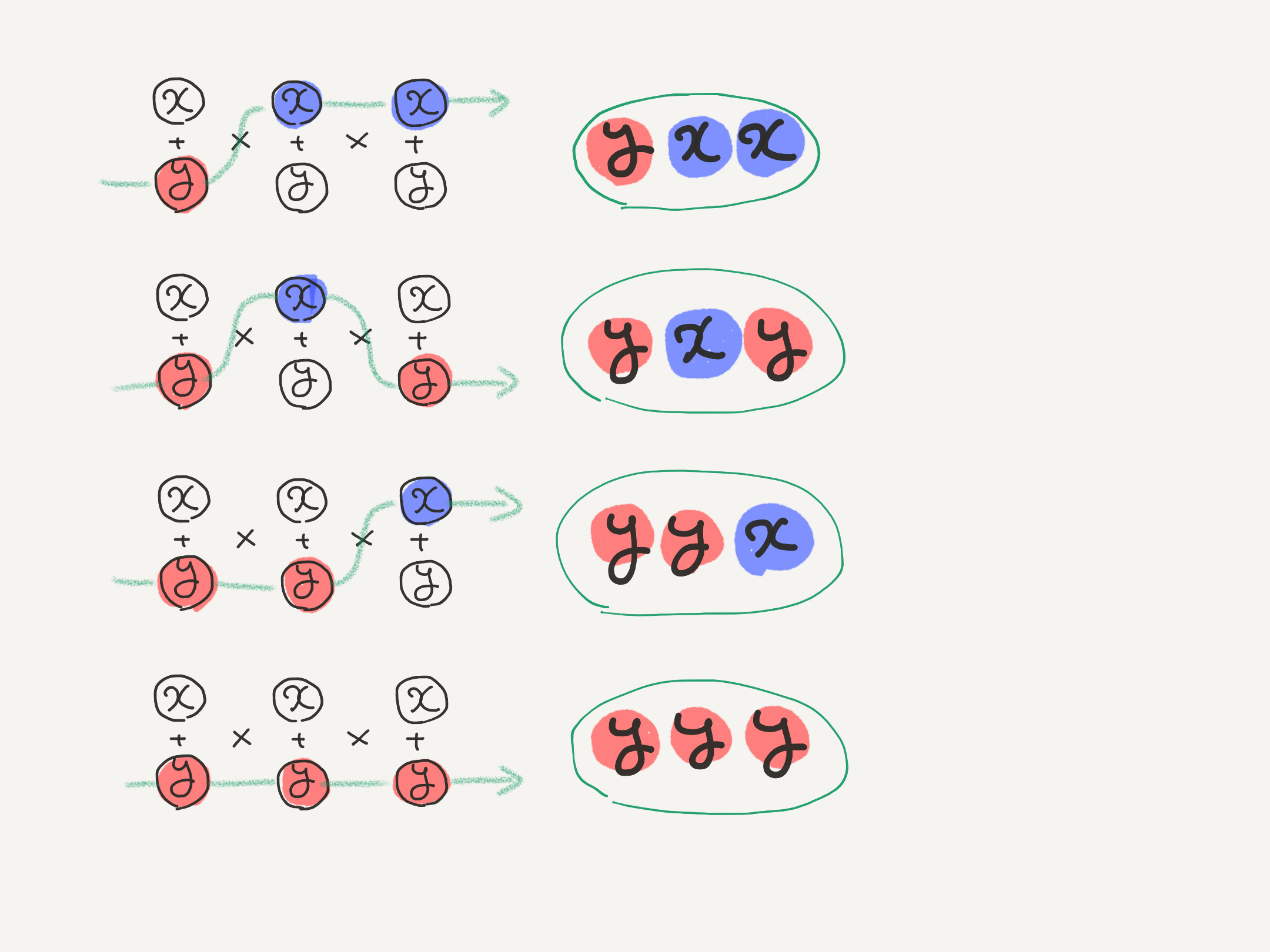
僕「そうだね。それって——」

テトラ「これって、二進法で数を数えていくのに似ていますよね。 $\MARKB{x}$ を $\MARKB{0}$ に、 $\MARKA{y}$ を $\MARKA{1}$ に見立てるんです！」

僕「……まったくその通りだね。何だか僕が補足しようと思ったところ、 すべてテトラちゃんがちゃんと先回りして考えていたんだね」

テトラ「ということじゃなくて、 あたしはもともと先輩からお聞きしたからです。 二項係数の話題のたびに書き出して、すっかり覚えてしまいました」

僕「そうなんだ。 そういえば、ユーリとパスカルの三角形の話をしたとき、 いまのテトラちゃんとそっくりのことを話した覚えがあるよ（第393回参照）。 僕の話、ワンパターン化しているのかな……」

テトラ「でもこんなふうにいろんな話がつながっていくのは、何度やっても楽しいです！　 本当に楽しい歌ならば、何度歌っても楽しいのと同じですよ！」

僕「なるほど」

テトラ「それに、 二進法で $000$ から $111$ まで表記するのはいかにも《すべてを尽くしている》って感じがしますし」

僕「うん、僕もそう思う。 いまのテトラちゃんの話で改めて思ったんだけど、 $$ \MARKA{1}x^3 + \MARKA{3}x^2y + \MARKA{3}xy^2 + \MARKA{1}y^3 $$ に出てくる $1,3,3,1$ というのは、展開して出てくるときの同類項の個数ってことになるね」