第380回シーズン38 エピソード10

内積と外積（後編）

登場人物紹介

僕：数学が好きな高校生。

テトラちゃん：僕の後輩。好奇心旺盛で根気強い《元気少女》。言葉が大好き。

ミルカさん：数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》。

$ \newcommand{\TEXT}[1]{\textbf{#1}} \newcommand{\REMTEXT}[1]{\textbf{#1}} \newcommand{\ABS}[1]{\bigl|#1\bigr|} \newcommand{\SQRT}[1]{\sqrt{\mathstrut #1}} \newcommand{\FOCUS}[1]{\fbox{ $\mathstrut#1$ }} \newcommand{\GEQ}{\geqq} \newcommand{\LEQ}{\leqq} \newcommand{\NEQ}{\neq} \newcommand{\PS}[1]{\left(#1\right)} \newcommand{\KAKUDO}[1]{#1^\circ} \newcommand{\VECV}[2]{\begin{pmatrix} #1 \\ #2 \end{pmatrix}} \newcommand{\VECVV}[3]{\begin{pmatrix} #1 \\ #2 \\ #3 \end{pmatrix}} \newcommand{\Fpara}{\vec F_{\parallel}} \newcommand{\Fvert}{\vec F_{\perp}} \newcommand{\Epara}{\vec e_{\parallel}} \newcommand{\Evert}{\vec e_{\perp}} \newcommand{\MAT}[4]{\begin{pmatrix} #1 & #2 \\ #3 & #4 \\ \end{pmatrix}} $

図書室にて

僕とテトラちゃんとミルカさんの《力学トーク》は続く。

等速円運動している質点の運動を定量的に考えているうちに（第378回参照）、話はベクトルの内積（第379回参照）からベクトルの外積へ移っていく。

内積から外積へ

ミルカ「私たちはいま、力のベクトルを二つの成分に分けて考えている。

一つは、回転軸となる原点と質点を結んだ直線方向で、いわば半径方向で、
一つは、その直線に垂直な方向で、いわば接線方向だ。

力を二つの成分に分解する（第379回参照）

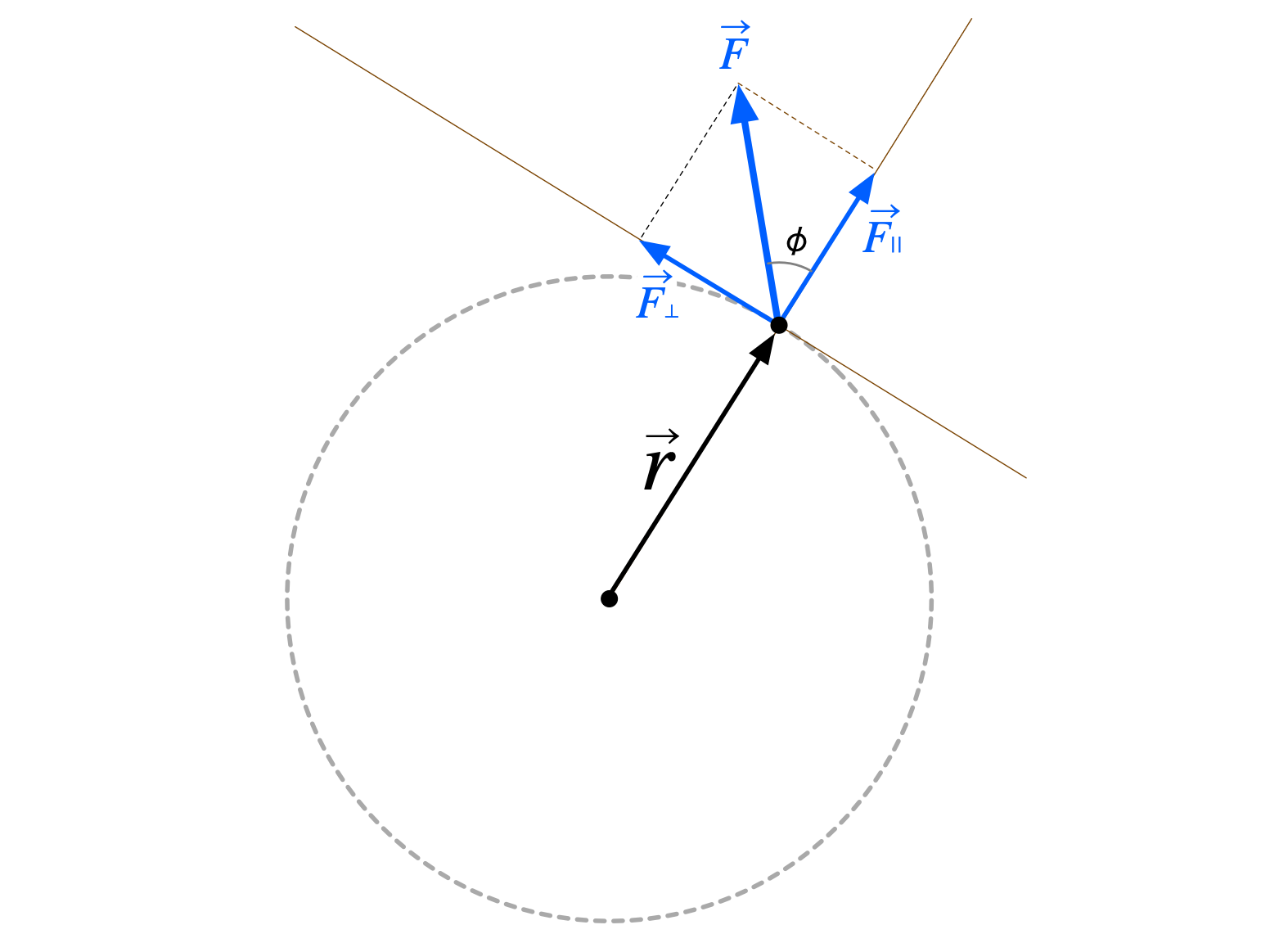
$$ \begin{align*} \Fpara &= \vec F\cos\phi \\ \Fvert &= \vec F\sin\phi \end{align*} $$

位置ベクトル $\vec r$ に平行な力の成分を $\Fpara$ とする（半径方向）。
位置ベクトル $\vec r$ に垂直な力の成分を $\Fvert$ とする（接線方向）。

僕「質点に掛かる力のベクトルを半径方向と接線方向の二つの成分に分けたんだね。

半径方向の成分は原点から離れていく向きの直線運動に関わる力で、
接線方向の成分は原点のまわりを回る回転運動に関わる力という話。

テトラ「なるほど。確かに、そう整理すると「回す」という意味が整理される……んでしょうか」

ミルカ「二つのベクトル $\vec a$ と $\vec b$ の内積は $\vec a \cdot \vec b$ と表し、次の式で定義される。ここで $\phi$ は二つのベクトルがなす角だ」

内積

二つのベクトル $\vec a$ と $\vec b$ の内積 $\vec a \cdot \vec b$ は、 $$ \vec a \cdot \vec b = \ABS{\vec a}\ABS{\vec b} \cos\phi $$ と定義する（$0 \LEQ \phi \LEQ \pi$）。

テトラ「はい、これは大丈夫です」

ミルカ「それでは外積だ。二つのベクトル $\vec a$ と $\vec b$ の外積は $\vec a \times \vec b$ と表す。このとき、外積の大きさは次の式で定義される」

外積の大きさ

二つのベクトル $\vec a$ と $\vec b$ の外積 $\vec a \times \vec b$ の大きさは、 $$ \ABS{\vec a \times \vec b} = \ABS{\vec a}\ABS{\vec b} \sin\phi $$ と定義する（$0 \LEQ \phi \LEQ \pi$）。

テトラ「なるほどです。確かに内積は $\cos$ で、外積は $\sin$ となっていて、二つの成分に——いえいえ違いますね！　《外積》じゃなくて《外積の大きさ》となっています」

僕「テトラちゃんの《乗り突っ込み》は珍しいなあ」

ミルカ「二つのベクトルの内積はスカラーになる。つまりここでは実数だ」

テトラ「はい」

ミルカ「しかし、二つのベクトルの外積はベクトルになる。いま書いた、 $$ \ABS{\vec a \times \vec b} = \ABS{\vec a}\ABS{\vec b} \sin\phi $$ という式は、二つのベクトルの外積として得られたベクトルの大きさを表す式なのだ」

テトラ「内積はスカラーで、外積はベクトル……ということなんですか」

僕「そうだね。慣れないととまどうけど、実数と実数の掛け算が実数になることを考えると、むしろ外積の方が普通の掛け算に似てるかも。実数×実数が実数で、ベクトル×ベクトルがベクトルになるという意味で」

テトラ「ははあ……そういえば、ベクトルの内積を学んだとき、内積の結果が実数になるのに混乱した覚えがあります。ベクトルの和はベクトルで、ベクトルの差もベクトルで、ベクトルの実数倍もベクトルで……でもベクトルの内積は実数になったからです。ベクトルの外積はベクトルなんですね」

ミルカ「外積の話を続けよう。二つのベクトルの外積はベクトルになる。そのベクトルの《大きさ》は $\ABS{\vec a}\ABS{\vec b} \sin\phi$ になる。そしてそのベクトルの《向き》は二つのベクトル $\vec a$ と $\vec b$ の両方に垂直になる」

テトラ「二つのベクトルに垂直な向きのベクトル？！　そんなものが存在するんですか？」

僕「空間ベクトルを考えればいいよね。だから、 $\vec a$ と $\vec b$ の二つのベクトルが作る平面を考えて、それに垂直な向きのベクトル。二つのベクトル $\vec a$ と $\vec b$ が作る平面を地上だと想像して、その平面から空に向かって行くか、地下に潜っていくか。その二つの向きのベクトルはどちらも $\vec a$ と $\vec b$ に垂直になる」

テトラ「あ、ああ……」

ミルカ「二つのベクトル $\vec a$ と $\vec b$ の外積 $\vec a \times \vec b$ の向きは、

ベクトル $\vec a$ の矢印を、
ベクトル $\vec b$ の矢印の向きに合わせるように回したときに、

右ネジが進む向きになる」

外積の向き

二つのベクトル $\vec a$ と $\vec b$ の外積 $\vec a \times \vec b$ の向きは、図のように定義する。

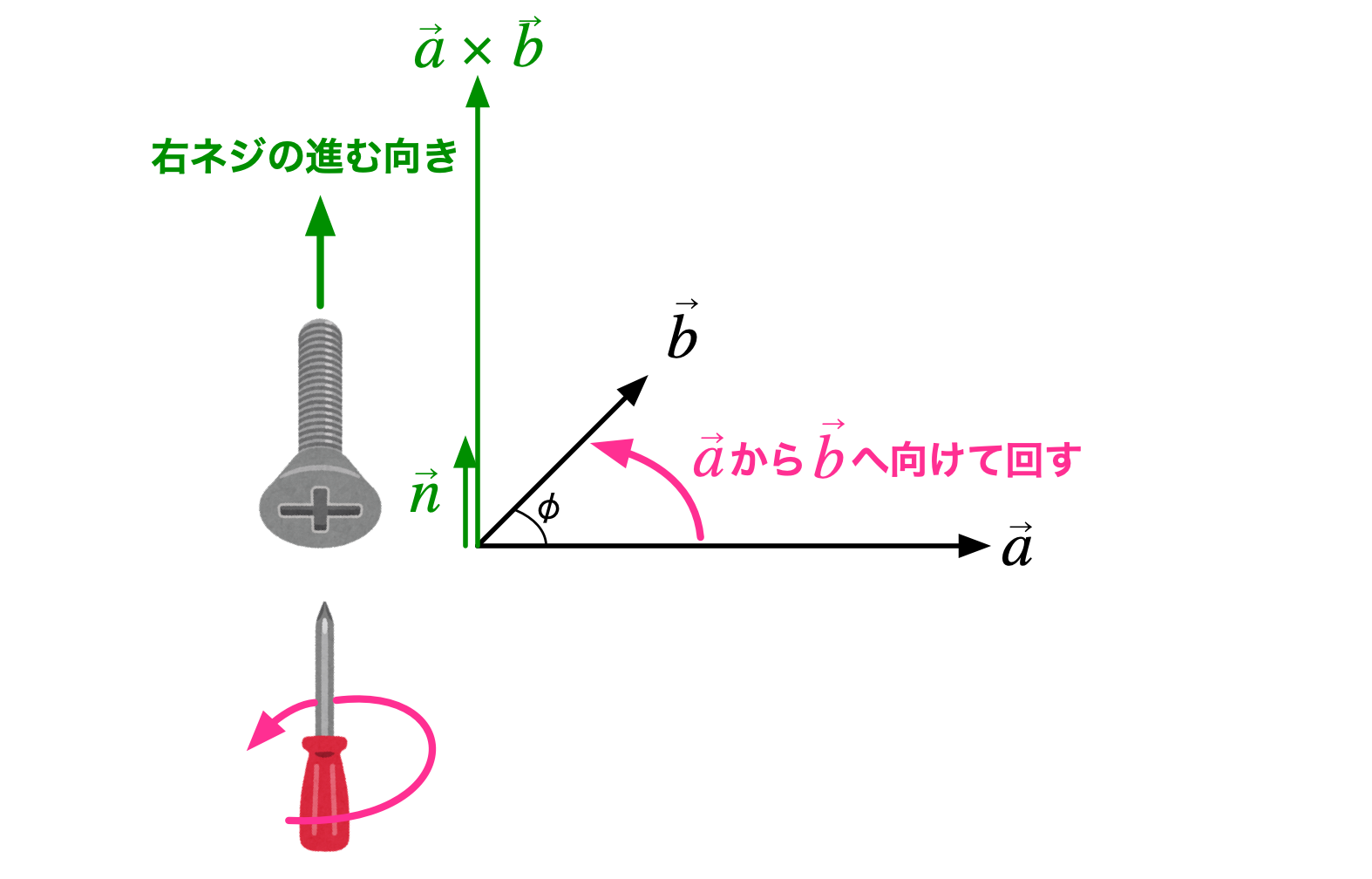
この向きの単位ベクトルを $\vec n$ で表すなら、 $$ \vec a \times \vec b = \underbrace{\ABS{\vec a}\ABS{\vec b}\sin\phi}_{\TEXT{《大きさ》}}\underbrace{\vphantom{\ABS{}}\vec n}_{\TEXT{《向き》}} $$ となる。

僕「$\vec a$ の矢印の向きから $\vec b$ の矢印の向きにドライバーを回したときに、ネジの進む向きだね」

ユーリ「おっ、時計回りに回すと締まるネジ登場！　壮大な伏線回収じゃん！（第371回参照）」

僕「（なんだいまの）」

テトラ「ええと……な、何となくはわかりましたが、外積の定義は、ずいぶん複雑ですね」

ミルカ「このように平行四辺形を描いて説明することもある。二つのベクトル $\vec a$ と $\vec b$ が作る《平行四辺形の面積》が《外積の大きさ》であり、その《平行四辺形に垂直な右ネジの進む向き》が《外積の向き》となる」

外積と平行四辺形

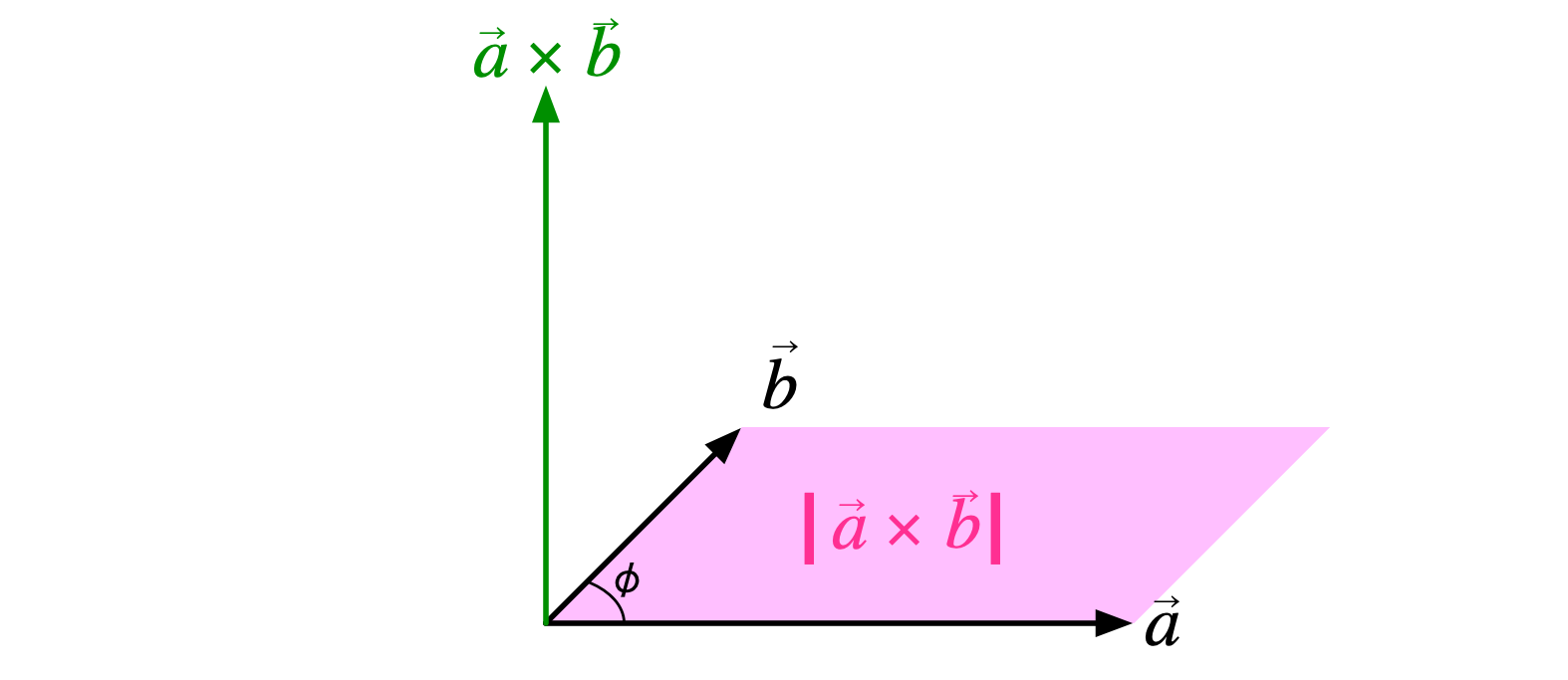
僕「この定義から、すぐに $$ \vec a \times \vec b = - \vec b \times \vec a $$ 出てくるね。どっちのベクトルをどっちの向きに回すかで逆回転になるから」

ミルカ「だから外積では交換法則が成り立たない」

テトラ「図が出てくるとわかりやすいんですけれど、かえって謎が増えてしまいました。どうして平行四辺形になるんでしょう……というか、『どうして平行四辺形になるんでしょう』という疑問を持つこと自体が変なんでしょうか」

ミルカ「そんなことはない」

僕「そんなことはないよ、テトラちゃん。これは外積というものの定義から考えると、平行四辺形の面積と見なせるという意味だね。ほら、もともとの話は、 $\vec r$ と $\vec F$ という二つのベクトルを考えていて、 $\vec F$ が $\vec r$ に垂直な方向にどれだけ寄与しているかを調べようとしていたんだよね」

テトラ「あ、はい、そうでした。 $\cos$ と $\sin$ の二つの成分にわけるというお話です。水平方向と垂直方向の落とした影のように」

僕「だよね。そう考えると、平行四辺形の面積が出てくるのは自然に感じるよ。だって、ほら、平行四辺形の面積というのは、こんなふうに底辺と高さの積を考えるんだけど、この《高さ》というのはまさに、斜めになった辺が、底辺に対して垂直な方向に落とした影の長さだから！」

平行四辺形の面積