第371回シーズン38 エピソード1

テコの原理（前編）ただいま無料

登場人物紹介

僕：数学が好きな高校生。

ユーリ：僕のいとこの中学生。僕のことを《お兄ちゃん》と呼ぶ。論理的な話は好きだが飽きっぽい。

$ \newcommand{\ABS}[1]{\left|#1\right|} \newcommand{\SQRT}[1]{\sqrt{\mathstrut #1}} \newcommand{\FOCUS}[1]{\fbox{ $\mathstrut#1$ }} \newcommand{\GEQ}{\geqq} \newcommand{\LEQ}{\leqq} \newcommand{\TEXT}[1]{\textbf{#1}} \newcommand{\NEQ}{\neq} \newcommand{\REMTEXT}[1]{\textbf{#1}} \newcommand{\PS}[1]{\left(#1\right)} \newcommand{\KAKUDO}[1]{#1^\circ} \newcommand{\SET}[1]{\bigl\{#1\bigr\}} $

僕の部屋

ユーリ「さあ！　ユーリちゃんの登場だよ！」

僕「……」

ユーリ「っていきなり無視かい」

僕「……見ての通り、忙しくて手が離せないんだよ」

ユーリ「電気スタンドと格闘するのに忙しくて、手が離せないと。手が離せないから、ユーリと話せないと」

僕「何だって？　いや、別に格闘してるわけじゃないよ……うん、これでできた」

ユーリ「何してたの？」

僕「電気スタンドのネジが少しゆるんでガタガタしてたから、ドライバーで締めてたんだよ。ほら、もう大丈夫」

僕は電気スタンドと手に持っていた大型ドライバーをユーリに見せた。

ユーリ「お兄ちゃん、そんなこともできるんだ」

僕「そんなことって、プラスドライバーでネジを締めただけだよ。ユーリはやったことないの？」

ユーリ「なくはないけど、あんまないかなー」

僕「ほら、ここのネジの頭にプラス（＋）の形のミゾがある。そして、ドライバーの先のギザギザも同じようにプラス（＋）の形になっている。ここを合わせて、ドライバーの持ち手を回す。時計回りに回すとネジが締まる」

ドライバーとネジ

※「いらすとや」さんのプラスドライバーのイラストとネジのイラストをもとにしています。

ユーリ「いやいや、さすがにネジの仕組みは知ってますけどー。時計回りに回すと締まるんでしょ。はっ！？　これって伏線？　右ネジの法則って何だっけ？」

僕「メタ発言自重。伏線って何だよ」

ユーリ「いえ、別になんでもございませんわ」

僕「ネジは時計回りで締まるのが普通だけど、特別なネジのときは、それとは逆の反時計回りで締まるようになっているのもあるよ」

ユーリ「そんなネジあるの？」

僕「ウチにある扇風機の羽根を止めるネジはそうなってた。夏に毎回組み立てるから覚えてるんだ。反時計回りに回すと締まる。きっとモーターの回る向きとの兼ね合いだろうね。そうしないと扇風機のスイッチを入れると羽根が外れちゃうのかも」

ユーリ「あはは！　『こんな扇風機はイヤだ：スイッチ入れたらバラバラになる』」

ユーリはドライバーをくるくる回しながら明るく笑った。

僕「ところでユーリは、どうしてドライバーの持ち手は太いか知ってる？」

ユーリ「そんなに太くないじゃん、このドライバー」

僕「全体の太さの話じゃなくて、ドライバーの先と持ち手を比べたときの話だよ。ドライバーの先は細いけど、持ち手は太いよね」

ドライバーの先は細く、ドライバーの持ち手は太い

ユーリ「えーと？　それは当たり前じゃないでしょーか。だって、先が太かったらネジに入らないし、持ち手が細かったら回しにくいもん」

僕「うん、そうだね。ユーリの言うとおり、当たり前といえば当たり前だ。ドライバーの先がネジに入らなかったら困るし、ドライバーが回しにくかったら困る。それでだ。持ち手が太いのは、持ち手に小さな力を加えるだけでネジを回すためと言えるね。小学校でも習ったテコの原理だ」

ユーリ「あれれ？」

僕「テコの原理、習ったよね。忘れちゃった？」

テコの原理

ユーリ「テコの原理は忘れてないけど、テコとドライバーは違うんじゃないの？　テコって、重いものを動かすための長い棒でしょ？」

僕「そうだね。テコの原理はいろんな言い方があるけど、たとえばこうなるかな」

テコの原理

曲がったり折れたりしない長い棒があり、図のように支点（してん）を中心にして回転するようになっている。

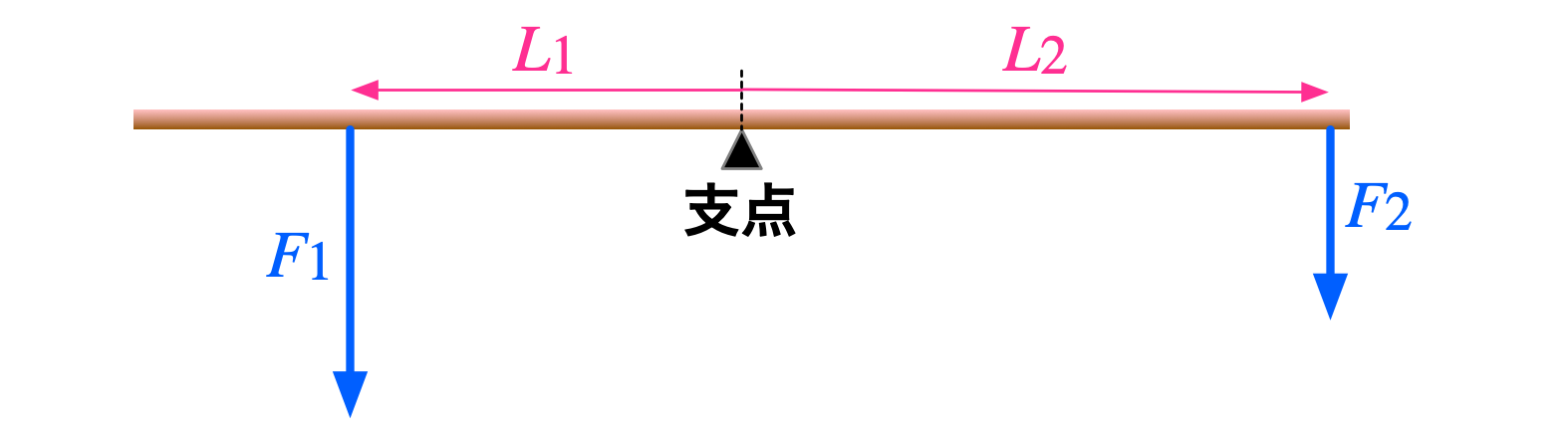
図にあるように、

支点からの距離 $L_1$ の点に大きさ $F_1$ の力を掛け、
支点からの距離 $L_2$ の点に大きさ $F_2$ の力を掛ける。

棒が回り出さないとしたら、 $$ F_1 L_1 = F_2 L_2 $$ という関係が成り立つ。

この関係をテコの原理という。

ユーリ「ん？」

僕「$F_1 L_1$ というのは $F_1$ と $L_1$ の掛け算だよ」

ユーリ「んにゃ、そこじゃなくて。あのね、ユーリが知ってるテコの原理だと、力点（りきてん）・支点（してん）・作用点（さようてん）が出てくるんだけど。力を掛けるのが力点で、動かないのが支点で、動かすおもりを置いておくのが作用点。『力点と支点の距離を倍にすると、作用点に置いたおもりの重さを倍にしてもいい』って覚えてる」

力点・支点・作用点

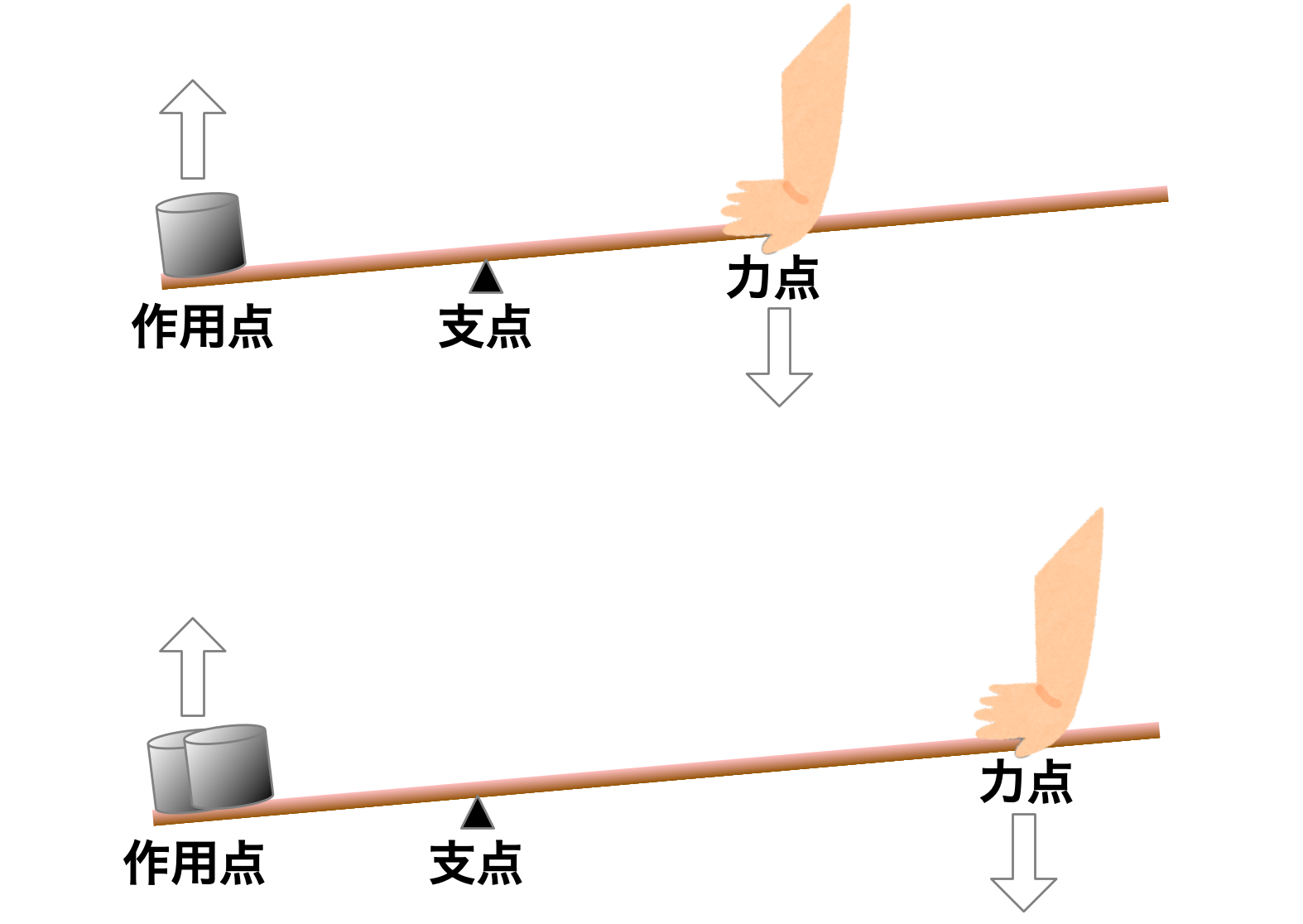
僕「うん。ユーリの言うのも間違ってはいないよ。ずいぶん大ざっぱな言い方だけどね。ユーリは「力を掛けるのが力点で、動かすおもりを置いておくのが作用点」といったけど、結局はどちらの点でも力の大きさを考えるのが大事になるんだ。おもりの重さというのは、結局は重力という力のことだからね」

ユーリ「あっ、その話、覚えてる」

【ＣＭ】

テトラ「はいっ、お話の途中ですが、お知らせです。力のこと、重さのこと、重力のこと……物理学の基礎となる『ニュートン力学』はこちらで学べます！」

僕「テコの原理を考えるときに、長い棒でおもりをゴロンと動かすイメージは悪くない。ぜんぜん悪くないんだけど、結局は力の大きさについて考えていることになるんだよ。もうちょっと詳しく説明するね」

ユーリ「ねーねー、力点・支点・作用点って意味ないの？」

僕「いやいや、意味がないわけじゃない。特に支点は大事だね。でも、力点は人間がテコに力を掛ける点で、作用点はおもりなどがテコに力を掛ける点。だから、力点と作用点は、人間がどういうふうにテコを使うかに関係している話だね」

ユーリ「ほほー」

僕「支点を中心にして回転する棒がある。その棒は曲がったり折れたりしないとする。そして、二箇所に力を掛けても棒が回り出さないことがある」

ユーリ「……」

僕「どういうときに回り出さないか。二箇所に掛ける力の大きさと、支点からのそれぞれの距離で決まる条件がある。その条件は、 $$ F_1 L_1 = F_2 L_2 $$ という等式で表される」

ユーリ「出たな数式マニア。お兄ちゃんは理科でも数式出すの好きだよねー」

僕「《数式は言葉》だからね。自分が思っていることをきちんと伝えるためには、言葉が大事になる。さもないとうまく伝わらない」

ユーリ「はいはい」

僕「もちろん、テコでおもりをゴロンと動かすときには、この等式がちょっと崩れることになる。例えば人間が掛けている力が $F_2$ だとすると、 $$ F_1 L_1 = F_2 L_2 $$ のときはまだテコは回らなくて、 $$ F_1 L_1 < F_2 L_2 $$ になったときにゴロンと行くわけだ」

ユーリ「人間の力 $F_2$ が大きければいいんだね」

僕「あるいは人間が力を掛ける点が支点から離れる……つまり $L_2$ が大きくてもいい。支点を中心に棒を回したかったら《力》を大きくする方法もあるし、《支点からの距離》を大きくする方法もある。要するに、テコの原理に出てくる、 $$ F_1 L_1 = F_2 L_2 $$ という式で注目すべきところは何かというと、

　《力の大きさ》と《支点からの距離》の両方を考える必要があるよ！

ってところなんだ」

ユーリ「ふんふん。なるほどにゃ」

僕「数式が出てきたときには『うわあ！』って嫌がるんじゃなくて、そういうふうに、じっくり読むといいんだよ」

ユーリ「ちょっと待ってよね。《先生トーク》が炸裂してるけどさー、ユーリは数式を嫌がってるわけじゃないもん！」

僕「それならいいんだよ。でもほら、数式を出すといつも『でたな数式マニア』って言うから……」

ユーリ「それはね。お兄ちゃんがいつも数式を持ち出すのを、からかってるだけなの。わっかんないかなー」

僕「僕をからかうのはいいんかい」

ユーリ「ユーリはいいの。テコの話を続けたまえ」

僕「はいはい。それでね、テコの原理では《力の大きさ》と《支点からの距離》の両方を考えるのが大事。大事なんだけど、さらに、 $$ F_1 L_1 = F_2 L_2 $$ という式をじっと見ると、

　《力の大きさ》と《支点からの距離》の積に注目するといいよ！

ということもわかる。積というのは掛け算の結果のこと。テコの原理の式を読むと、

左辺は $F_1$ と $L_1$ の積である $F_1 L_1$ で、
右辺は $F_2$ と $L_2$ の積である $F_2 L_2$ で、
この左辺と右辺は等しい。

という関係があることがはっきりわかる」

ユーリ「そんなの、式見ればわかるよ」

僕「もちろん、式を見ればわかる。そしてこの式、 $$ F_1 L_1 = F_2 L_2 $$ をよく読めば、さっきユーリがテコの原理で説明してくれた『力点と支点の距離を倍にすると、作用点に置いたおもりの重さを倍にしてもいい』という表現をはっきりと確かめることができる」

ユーリ「えっえっ、いま何て言った？」

僕「ユーリが説明してくれたテコの原理を、この式で確かめることができるって言ったんだよ」

ユーリ「どゆこと？」

図A: 手の力でおもりを支える

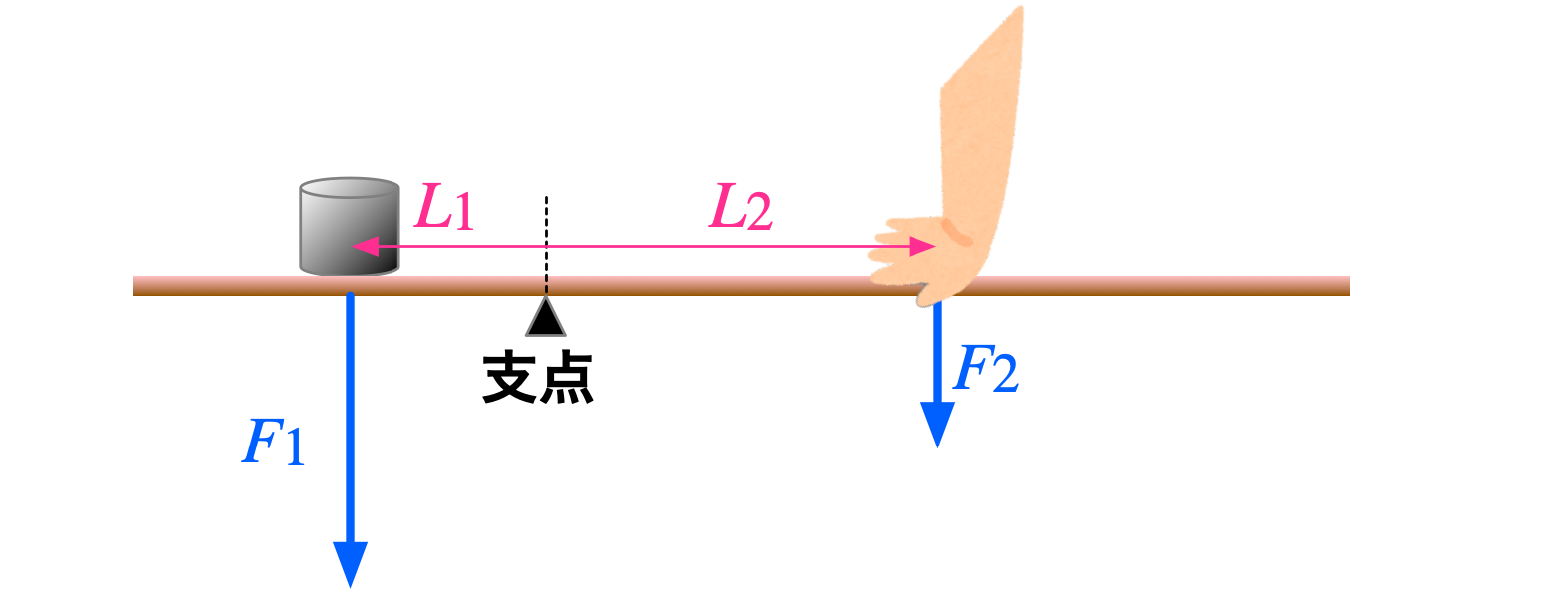
僕「この図Aのように、支点のまわりに回転する棒があって、片方におもりがあり、他方を手で持っているようすを考える」

ユーリ「うん」

僕「棒が回転しないなら、テコの原理から、 $$ F_1 L_1 = F_2 L_2 $$ が成り立っている。こんなふうに《式で表している》から、

おもりの重さ $F_1$
おもりの支点からの距離 $L_1$
手が加える力の大きさ $F_2$
手の支点からの距離 $L_2$

という $F_1,L_1,F_2,L_2$ の関係を定量的に表せていることになる」

ユーリ「ていりょうてき」

僕「そう。関係を大きい／小さいみたいな定性的な表現で表すんじゃなくて、こちらがどれだけの大きさのときは、あちらはどれだけの大きさになる……みたいにはっきりと定量的な表現で表しているということ」

ユーリ「わかる」

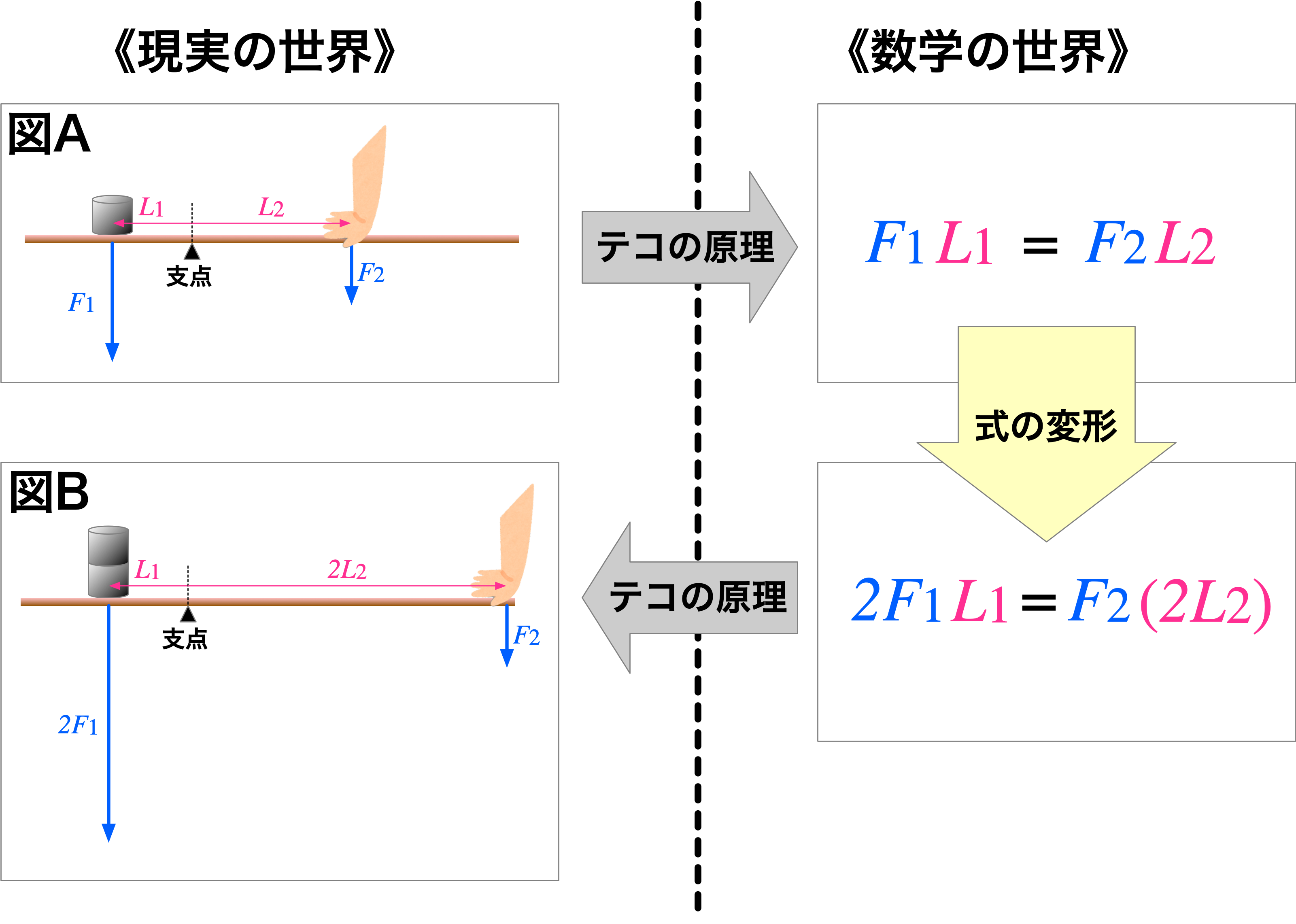
僕「そしていま、図Bのように、手の力を掛ける点を動かして、支点からの距離を $L_2$ から $2L_2$ にしたとする。これがユーリの言う『力点と支点の距離を倍にする』という意味だよね。そうすると、二つ分のおもりを支えることができる。つまり、 $F_1$ を $2F_1$ にして『作用点に置いたおもりの重さを倍』にできる」

図B: 手の位置を変えて二つのおもりを支える

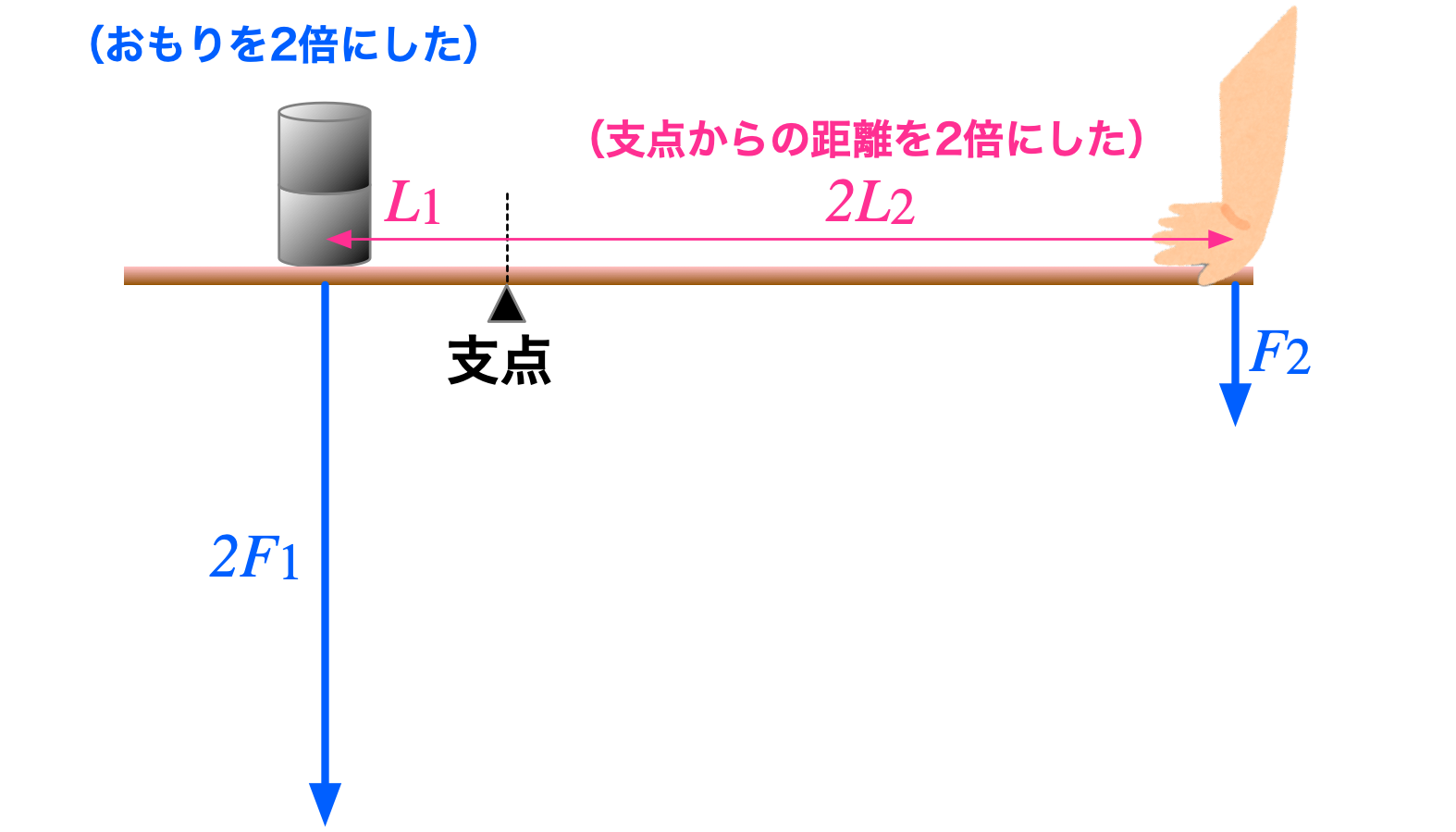
ユーリ「そーそーそー！　こういうことを言いたかったの！」

僕「テコの原理を使うと、図Aが成り立っているときに、図Bが成り立つことが証明（しょうめい）できるわけだ」

ユーリ「ええっ？　証明？」

僕「図Aが成り立っているということは、テコの原理から、 $$ F_1 L_1 = F_2 L_2 $$ という式が成り立つことがいえる。この式が成り立つなら、両辺に $2$ を掛けた $$ 2(F_1 L_1) = 2(F_2 L_2) $$ も成り立つ。ということは、 $$ (2F_1) L_1 = F_2 (2L_2) $$ も成り立つことが言える。そしてこの最後の式は、図Bが成り立つことを示している」

ユーリ「……」

僕「いまのは、テコの原理を使って、図Aが成り立つときに図Bが成り立つことを証明したんだ」

ユーリ「証明って、数学の話だけだと思ってたよー。理科でも証明ってあるの？」

僕「あるよ。理科に限らないけど、何かの現象や何かの性質を数式で表すってそのためだからね。数式で表すのは、数学という強力な道具を使うためだから。数式で表せば、式の変形や代入やその他いろんなことが使えるようになる。さっきの『両辺に $2$ を掛ける』というのはその簡単な例だね」