第356回 シーズン36 エピソード6

立方体倍積問題で《予言者読み》をやってみよう（後編）

本の《予言者読み》

僕「ここまで読んできたことをヒントにして、本の先に何が書いてあるのかを読む前に言い当てる。 ……そんな本の読み方を、僕は《予言者読み》と呼んでるんだ。 まるで予言者のように先に書いてあることを当てられたらおもしろいよね。 特に、数式という巨大なヒントを見ちゃったあとなら、ガチで考えることができる」

ユーリ「本の《予言者読み》、何だかおもしろくなってきた。 答えを見ないように、見ないように少しずつ読んでくんでしょ？　もっとやろーよ！」

僕「じゃあ、引き続き、先を読んでいくか。 二つの比例中項 $a:x = x:y = y:b$ を求める問題が、 どうして立方体倍積問題に出てくるのかはよくわかった（第355回参照）から、 その続きを読んでいこう」

ユーリ「そして、数式が出てきたら、お兄ちゃんは叫び声を上げて、ばたっと本を閉じる！」

僕「いや、もう叫ばないし、本を閉じるのもやめるよ。この紙で先の部分を隠しながら、少しずつ読んでいこう！」

ユーリ「おー！」

メナイクモス

僕「ヒオスのヒポクラテスが二つの比例中項を考えたところの次から……」

ユーリ「メナイクモスの解法だって」

僕「っと、ここで止めよう！　ここまでで《予言者読み》ができそうだよ」

ユーリ「えーっ、もうちょっと先まで読んだら解法がわかるのに？」

僕「だからだよ。もう十分にヒントが出てる。考えようよ」

ユーリ「まだ数式出てきてないよ。ナントカ曲線が出てきただけじゃん」

僕「メナイクモスは放物線と双曲線を使ったって書いてある。 放物線と双曲線を使って、 $a:x = x:y = y:b$ の $x,y$ を求めるんだ。これはできるよ」

ユーリ「さっぱりわからん」

僕「さっき、ユーリが書いてくれた連立方程式のことだよ（第355回参照）」

$$ \begin{cases} ay &= x^2 \\ bx &= y^2 \end{cases} $$

ユーリ「これが放物線？」

僕「$ay = x^2$ から、$$y = \tfrac{1}{a}x^2$$が得られるから、このグラフを描けば放物線になるよね」

ユーリ「あー、その式で一つの放物線になるってことね」

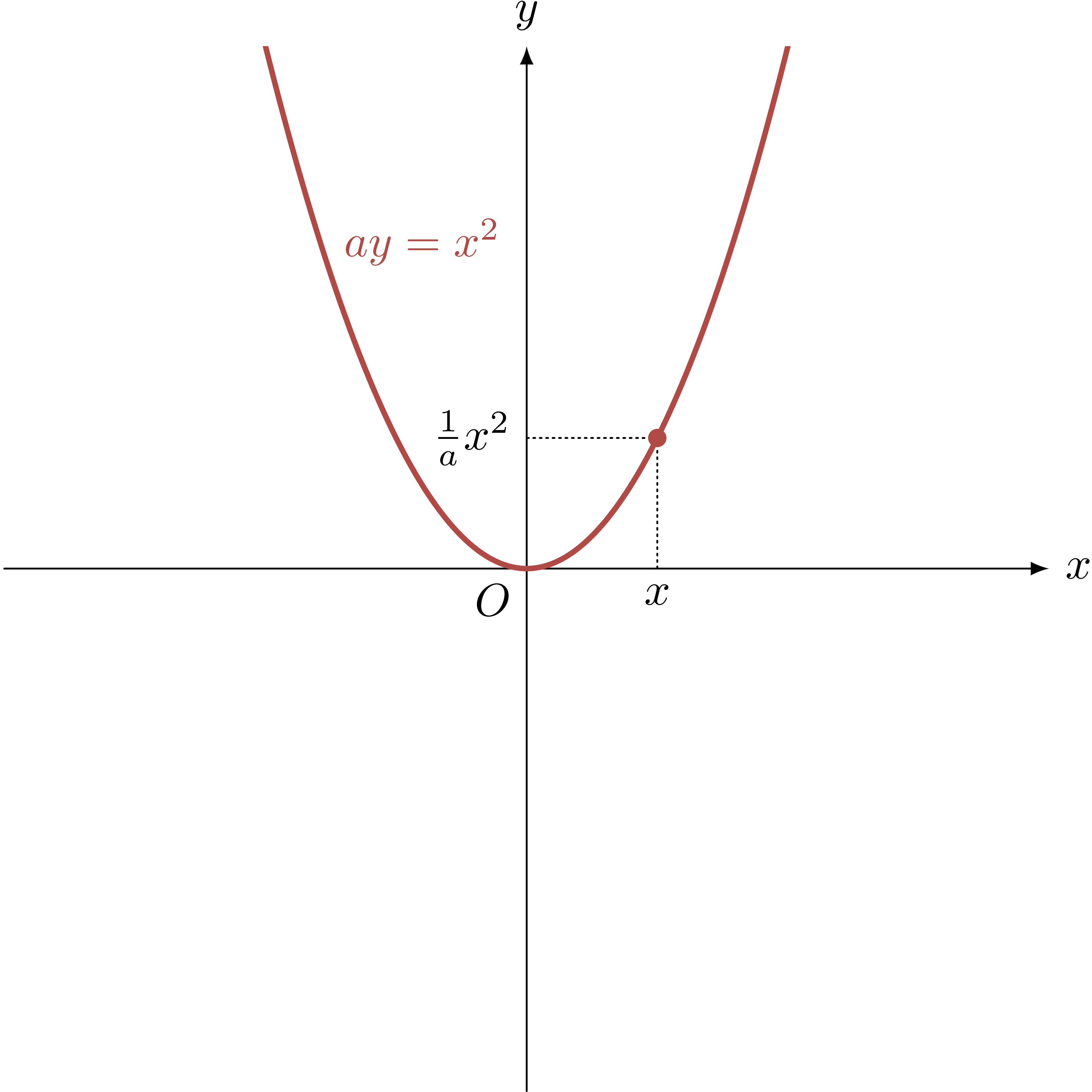
僕「グラフを描くってことは、 $x$ 座標の値と $y$ 座標の値の関係を曲線として表していることになる。 このグラフの場合、この曲線上にある点 $(x,y)$ は必ず、 $ay = x^2$ という関係を満たしているし、 この曲線上にない点はその関係を満たしていないといえるから」

ユーリ「$bx = y^2$ はどーなんの？」

僕「こっちも放物線だね」

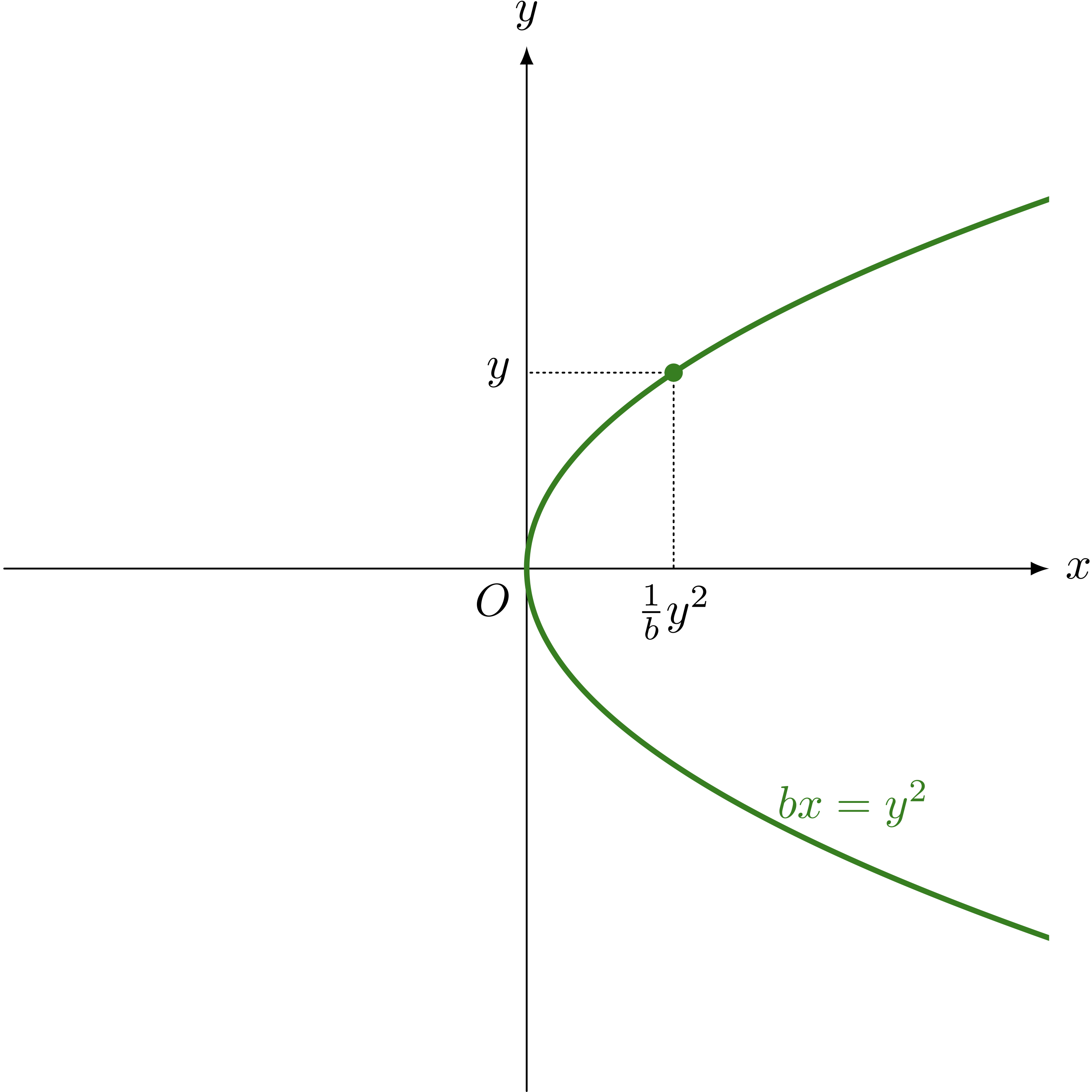
ユーリ「$bx = y^2$ だと、放物線は横に転がるってことかー」

僕「そうだね。『横に転がった』と言っても悪くないけど、どちらかといえば『鏡に映すように反転した』かな」

ユーリ「細かい突っ込み入った」

僕「$bx = y^2$ から、$$x = \tfrac{1}{b}y^2$$が得られるけど、この放物線は、$$y = \tfrac{1}{b}x^2$$の $x$ と $y$ が入れ替わった形になってる。ちょうど $y = x$ という直線に鏡を置いて、そこに映した形になるんだね」

ユーリ「あ、そーゆー意味か」

連立方程式

僕「それで、この連立方程式を満たす $x$ と $y$ を見つければ $a:x = x:y = y:b$ の $x,y$ を求めたことになる。 それは、 $ay = x^2$ と $bx = y^2$ という二つの放物線が交わった交点を求めることになる。 それは二つの放物線の交点は、両方の関係を満たしていることになるから」

$$ \begin{cases} ay &= x^2 \\ bx &= y^2 \end{cases} $$

ユーリ「えーと……なにをしたいんだっけ」

僕「もちろん、立方体倍積問題だよ」

• 立方体倍積問題は、 $A$ が与えられて $B^3 = 2A^3$ を満たす $B$ を求めれば解ける。
• そしてそれは、 $X^3 = 2$ を満たす実数 $X$ を求めれば解ける。
• そしてそれは、ヒオスのヒポクラテスが見つけた比例中項 $a:x = x:y = y:b$ で $b = 2a$ にしたときに相当する。
• なぜなら、 $a:x = x:y = y:2a$ から $x^3 = 2a^3$ が得られるから。

ユーリ「んー……てことは放物線の交点の $x$ 座標が答え？」

僕「そうだね。 $b = 2a$ として、二つの放物線の交点を求める。すると、その $x$ 座標は $\sqrt[3]{2}$ になっている……というのが、メナイクモスの解法なんだと思うよ！」

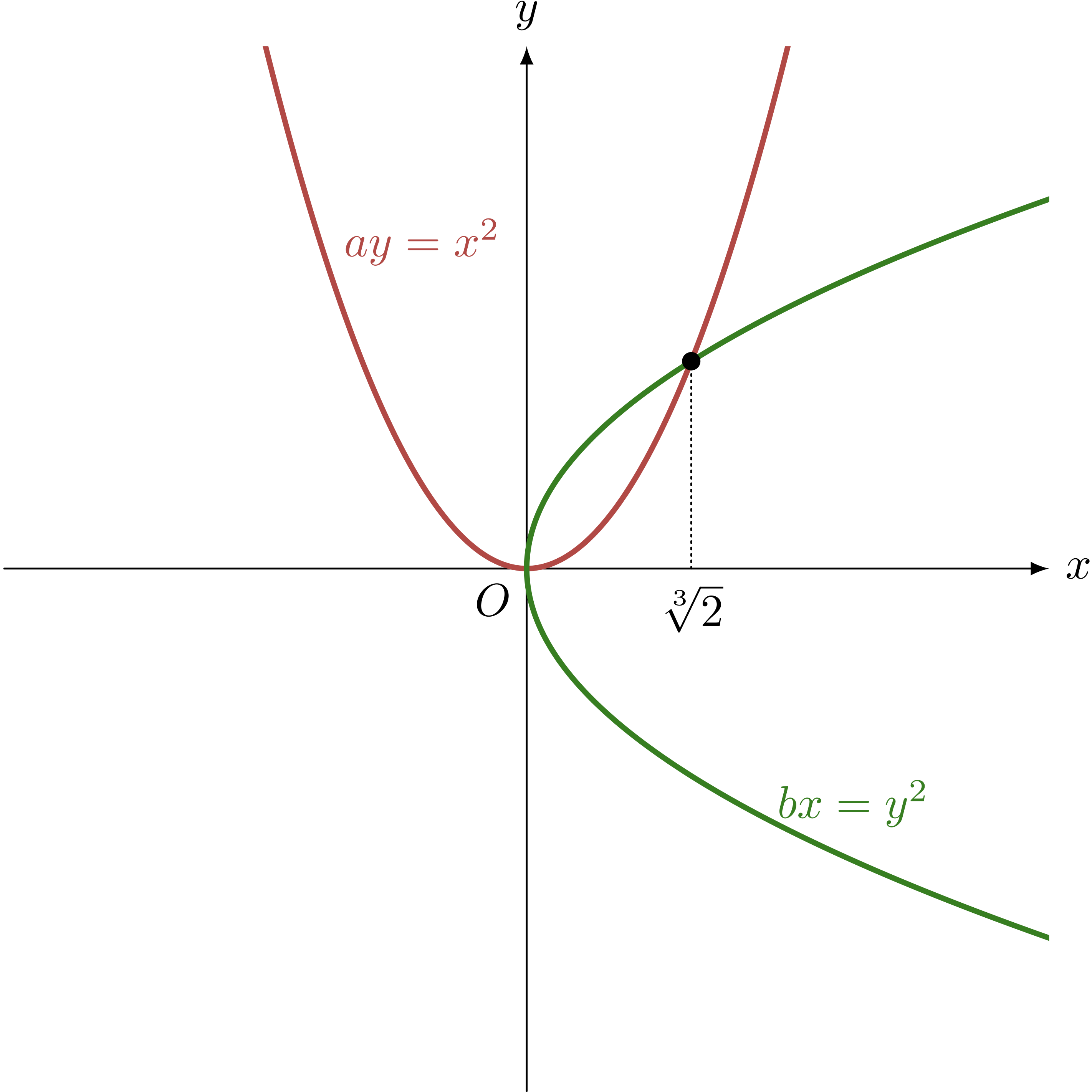
ユーリ「お兄ちゃんの《予言者読み》ってすげー！　本読む必要ないじゃん！」

僕「いやいや、そんなことないよ。本からヒントをたっぷりもらって、最後の一歩を考えただけだから」

ユーリ「だって、本には数式、何も書いてなかったよね」

僕「放物線を使ったと書いてあったから、あとは知識でいける。 じゃあ、本の続きを読んで《予言者読み》の答え合わせをしよう！」

ユーリ「あっ！！」