第332回 シーズン34 エピソード2

直列つなぎと並列つなぎ（後編）

僕の部屋

僕「直列と並列がペアになっていて双対（そうつい）と呼びたくなる場面は、もっと別のところにも出てくるよ。たとえば……

• 直列につなぐと $R = R_1 + R_2$ になる。
• 並列につなぐと $1/R = 1/R_1 + 1/R_2$ になる。

……というのもそうだね」

ユーリ「は？」

僕「だよね？」

ユーリ「いやいやいやいや。『だよね？』じゃないよ、お兄ちゃん。説明なしでいきなりポンポコポンポコ式を出されても困るんですけどー」

僕「そうか、そうだね。ごめんごめん」

ユーリ「『わかった。じゃあ、かわいいイトコのユーリのために、順を追って話そう。 大丈夫、いっしょに進めば難しくはないよ』」

ユーリ「『うん！』」

ユーリ「『こんなふうにして、僕とユーリの新しい旅が始まった。直列と並列をめぐる冒険の旅が』」

僕「ひとり芝居、終わった？」

ユーリ「終わった」

回路

僕「じゃあ、ユーリのために順を追って話そう。 といってもユーリだって知ってることはたくさんあると思うんだけどね。 まずは回路から」

ユーリ「かいろ」

僕「電池と豆電球とそれからスイッチを使って、豆電球をつけたり消したりした。《点灯》と《消灯》だね。こんなふうに部品をつないで作ったものを《回路》という」

ユーリ「うん」

僕「電池の《+極》（プラスきょく）から導線（どうせん）をつないで、豆電球に来て、豆電球から導線をつないで電池の《-極》（マイナスきょく）までつながると、豆電球が点灯する。このとき、導線をたどってぐるっとまわることができる。 これを《閉じた回路》と呼ぶこともある」

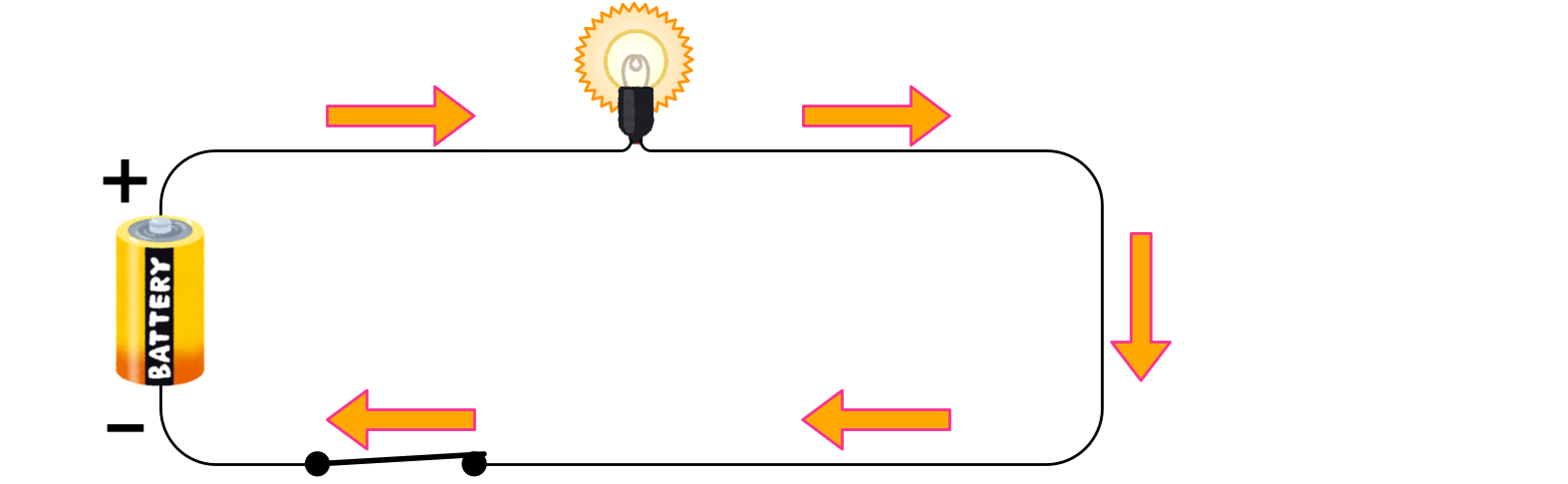
ユーリ「ふむふむ」

僕「電池の《+極》から《-極》までぐるっとまわることができないと、豆電球は点灯せずに消灯する。 これを《開いた回路》と呼ぶこともある。 ぐるっと回れるかどうかがとても大事なんだ」

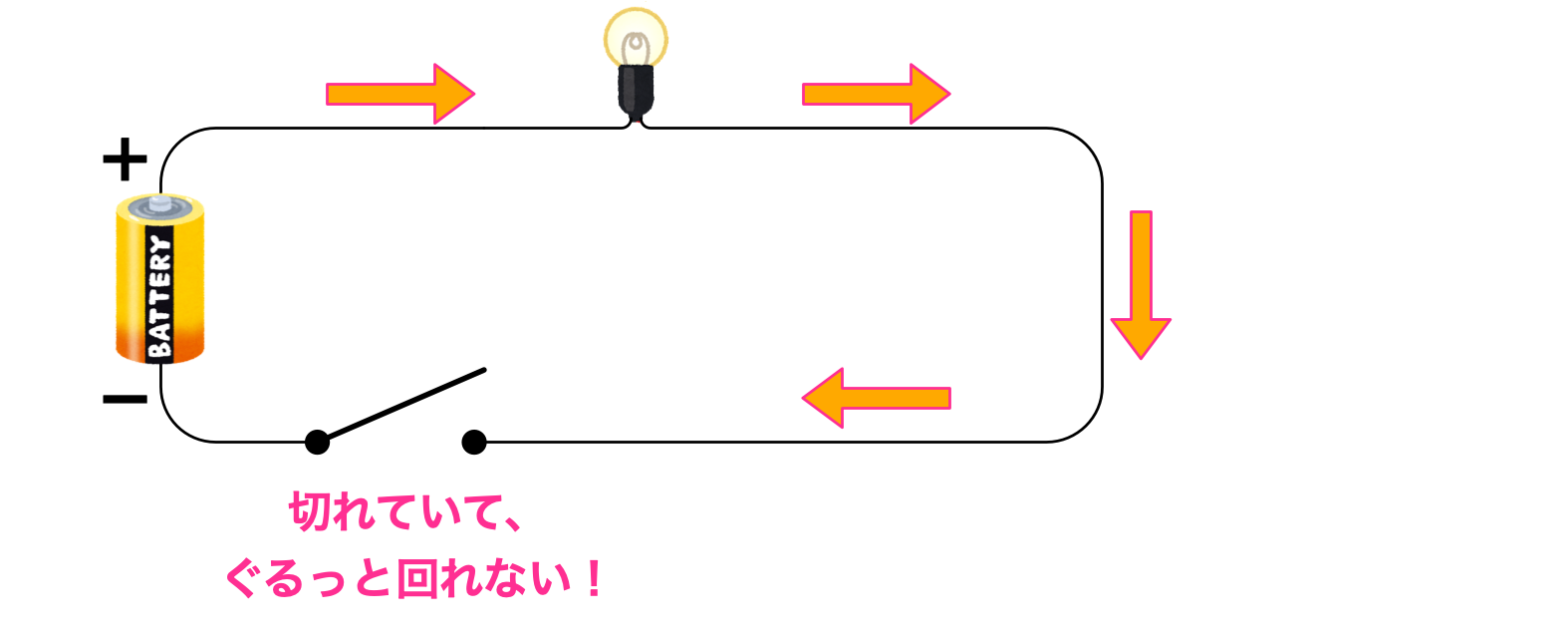
ユーリ「いいよん」

僕「毎回、何もないところから回路を作って豆電球を点灯・消灯するのはたいへんだから、 スイッチという部品があるともいえる。スイッチをオンにすれば回路が閉じて豆電球が点灯し、 スイッチをオフにすれば回路が開いて豆電球が消灯する」

ユーリ「何も難しくない」

僕「いいことだ。電池とスイッチと豆電球をつないでできる回路はとっても簡単だね。 記号を使ってこんなふうに表すことがある」

ユーリ「知ってる」

僕「豆電球は左右対称で特に向きはない。スイッチは記号では向きがあるけど、部品としての向きはない。 でも電池は違う。電池には《+極》と《-極》があるから、記号でも区別している。長い方が《+極》で、短い方が《-極》」

僕「お、飽きてきた？」

ユーリ「体内に不足している酸素を取り込んでおるだけじゃ。決して、お兄ちゃんの話す内容がつまらないとか、 ぜんぶ知ってるとか、もっと早く話を進めろとか、直列と並列はどーなったとか、そう思っているわけじゃないぞよ」

僕「心の中が《だだ漏れ》してるなあ……わかった。もう少しテンポを上げようか」

ユーリ「よっしゃ」

回路を回るもの

僕「回路のことをサーキットという。 F1みたいな自動車レースをする場所をサーキットというけど、それと同じ。 ぐるっと回ってくる場所だからだね」

ユーリ「ゴーカートのサーキットもある」

僕「そうだね。スタートからぐるっと回ってゴールまで来るんだけど、またそこから再スタートしてぐるぐる回れる場所、それがサーキット。 F1レースのサーキットだったら、フォーミュラカーというレーシングカーが回っている。 ゴーカートのサーキットだったら、ゴーカートが回っている。 だとしたら、電池と豆電球を導線でつないだサーキットでは《何》が回っているんだろう」

ユーリ「電気」

僕「うん、それでだいたいは合ってるんだけど、正確には回路を回っているのは電子（でんし）と呼ばれる小さなものだね」

ユーリ「あ、電子も知ってる。電気と電子って違うもの？」

僕「電気というのはとても広い意味を持った一般的な表現だね。 豆電球が点灯することを《電気がつく》といったり、そのときに《電気が流れる》といったり、 人によっては《電気が来てる》や《強い電気》みたいな言い方をする。 それはそうなんだけど、 《電気》というだけだと大ざっぱすぎるから、 理科で電気の勉強をするときには、もっと正確に考えるために用語を注意して使う」

ユーリ「電子って粒でしょ？　理科の教科書に出てきた」

僕「そうだね。電子は粒と見なすことができる。 でも『電子は何か』というのは、ちゃんと考えると難しい話になる。 ふだん僕たちが見ている『物体』は原子からできていて、電子はその原子を構成しているものの一部だから、 僕たちが考える『物体』とそのまま同じイメージで考えるのは難しいときもある。 でもいまは電子のことを導線を流れる小さな粒と見なすことにする」

ユーリ「ふーん」

僕「導線は金属でできていて、そこには自由電子（じゆうでんし）と呼ばれる電子がとってもたくさんある。 自由電子は、自由に動き回ることができる電子。 電球が点灯しているときには、閉じた回路の中をその電子がぐるぐると回っているんだ。 電子はとってもたくさんあって、とっても小さいから、電子が流れていると考えるのがぴったりする」

ユーリ「理科の教科書にもあったよ。導線を流れる電子の粒。実際は何個くらい？」

僕「ものすごくものすごくたくさんだね。図に描くとしたらせいぜい10個や100個くらいだけど、 アボガドロ数を考えると、 実際に豆電球を点灯させる回路で流れている自由電子は、10の20乗くらいはあるんじゃないかな」

ユーリ「10の20乗って、流れてる電子の数が？」

僕「ざっくりとした数だけどね。もちろん使っている金属の量による」

ユーリ「10の20乗……どのくらい多いのかさっぱりわからん」

僕「ああ、そうだよね。たとえば、世界の人口は数十億人だけど、ざっと100億人とする。 100億だと1の後に0が10個続く。 $$ 100\REMTEXT{億} = 100{}0000{}0000 = 10^{10} $$ つまり世界の人口は多く見積もって10の10乗程度といえる」

ユーリ「てことは、流れている電子は《10の20乗》なんだから、世界の人口の倍くらいってことか……確かに多いね」

僕「え、違うよ違うよ。10の20乗は《10の10乗》の2乗だよ」

ユーリ「おっおっ？」

僕「自由電子の数は、ざっくり言えば、1の後に0が20個続くんだ」

ユーリ「さっぱりわからんの2乗だよー！」

僕「こんなふうに考えてみようか。 地球をこんなふうにビーチボールみたいなものだと考える」

ユーリ「はあ」

僕「そして、世界にいる100億人全員がビーチボールみたいな大きさの地球を抱えているとする」

ユーリ「100億個のビーチボール……」

僕「そして、どのビーチボールの上にも100億人の《小さな人》が住んでいると考える。そのとき、その《小さな人》の数はぜんぶで100億×100億になる。これが10の20乗という数だね」

ユーリ「はあ？　はーーーあっ？？　何それ！　ヤバくない？　そんなにたくさんの電子が流れてるの？　導線の中を？？　ありえなーい！！」

僕「すごいよね。 $10^{20}$ っていうのはそのくらい大きな数になる。 豆電球を点灯するだけで、それだけの自由電子が動く。そうなると、一個一個の電子のようすを考えるだけじゃなくて、 たくさんの電子がまるで川のように流れているようすを考えることに意味がある。 それはわかるよね」

ユーリ「わかる」

僕「一個一個の電子のようすを考えるみたいに、すごく小さなところに注目して考えるのは《ミクロな視点》と呼ぶことがある。ミクロっていうのは小さいって意味だね。 それに対して、一個一個の電子のようすを考えるんじゃなくて、電子の流れみたいなもっと大きなところに注目して考えるのは《マクロな視点》と呼ぶ。マクロは大きいって意味」

ユーリ「……」

僕「《ミクロな視点》と《マクロな視点》はどちらも大事。ミクロな視点に立って考えるなら、細かいところまで正確にわかるかもしれない。でも全体の振る舞いはかえってわかりにくくなることもある」

ユーリ「一人のことを考えていたら、世界のことがわからなくなるみたいに？」

僕「そうだね！　ユーリはよく頭が回るなあ！　まさにそうだよ」

ユーリ「でも、一人一人も大事だよね」

僕「もちろん。世界を成り立たせているのは一人一人なんだからね。電子の流れがどうなるかは、一個一個の電子がどうなっているかで決まる。だから、《ミクロな視点》と《マクロな視点》はどちらも大事。 そして、いま自分がどちらの視点で考えているのかを意識するのも大事」

ユーリ「にゃるほどね」

電子の流れ

僕「ところで、さっきは『川の流れ』と言っちゃったけど、導線の中を電子がすごい速度でビューン！と流れているわけじゃない」

ユーリ「え、そーなの？　光の速さで流れるんじゃないの？」

僕「電子が導線の中を流れていく速さは、1秒で1mmも動かないくらいの遅さなんだ。ざっくりとした話だよ」

ユーリ「ダウト！」

僕「え？」

ユーリ「お兄ちゃんの話、明らかにおかしーもん。 電子が1秒に1mmしか進まないなら、10cm進むのに100秒も掛かることになるじゃん。 スイッチ入れました……しばらくして、はいっ！　いま豆電球光りました！ になっちゃう。 だから、電子の速さが1秒で1mmって絶対に変でしょ？」

僕「ユーリは賢い。その指摘はすばらしいよ。実際、スイッチ入れてから豆電球がつくまでの距離と時間を考えると、その速度は光速度になる。でもそれは電子の速度じゃないんだ」

ユーリ「だってだって、スイッチ入れて豆電球が光るのは電子が流れているからだよね。 それなのにスイッチ入れてから豆電球がつくまでの速度は電子の速度とは違うの？」