![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「ねー、お兄ちゃん。何かクイズない?」
僕「いきなり何だよ」
ユーリ「いきなりじゃないもん。さっきからずっと思ってたもん」
僕「ユーリがずっと思ってても、言葉にしなくちゃ僕には伝わらないよ」
ユーリ「へいへい。そーですねっと」
僕「クイズねえ……」
今日は土曜日。ここは僕の部屋。いつものように、いとこのユーリが遊びに来ている。
小さいころから一緒に遊んでいるから、彼女は僕のことを《お兄ちゃん》と呼ぶ。
ユーリ「『小さいころから一緒に遊んでいる』……だから……『《お兄ちゃん》と呼ぶ』……そこには、ロンリのヒヤクがあるんじゃね?」
僕「メタ発言自重」
ユーリ「だって気になるじゃん」
僕「地の文にツッコミ禁止」
ユーリ「そのくらい退屈だぞって、言葉にして伝えてるんだもん!」
僕「はいはい。そうですねっと」
ユーリ「いーから、クイズ!」
僕「それじゃあね、こんなクイズはどうだろう」
ユーリ「お兄ちゃん、やればできる子」
クイズ(電球の点灯・消灯)
階段の途中に電球が一つあります。
また、スイッチAとスイッチBの二つのスイッチがあります。
どちらのスイッチでも電球をつけること(点灯)ができ、 どちらのスイッチでも電球を消すこと(消灯)もできるようにしたいと思います。
どんなふうに配線したらいいでしょうか。

僕「問題の意味はわかるよね」
ユーリ「わかる。暗い階段を降りるのあぶないから、上で電気つけて、降りて、下で電気消したいんでしょ?」
僕「そうだね。せっかく降りたのに電気を消すためにまた階段を昇るなんて無意味なこと、やりたくないからね」
ユーリ「無限ループに入っちゃうし」
僕「また降りるために電気をつけて……降りて……電気を消すためにまた上がって……」
ユーリ「こーゆースイッチ、学校にもあるよ」
僕「えっ、あったっけ?」
ユーリの中学校は、僕が卒業した学校だ。 こんなスイッチあったっけ……?
ユーリ「体育館の講壇、あるじゃん? 講壇下の地下室がそーなってた。 右側と左側に狭い入口があって、どっちにもスイッチがあって、どっちでも点灯できるし、どっちでも消灯できるようになってたよ」
僕「ちょっと待って。講壇下の地下室って何だ?」
僕が首を傾げているのを見て、ユーリはなぜか得意げに話し出す。
ユーリ「お兄ちゃん、知らないの? 講壇の下って物置みたいになってるんだよ」
僕「へえ、空間があるんだ」
ユーリ「中に、卒業式とか入学式で使う椅子なんかが置いてあるの。 ユーリ、委員だったときに中に入ったことある。ちょっとこわくて面白かった。 先生が電気つけて入ってるときに、 反対側の入口で誰かがイタズラして電気消したら先生が怒ってた」
僕「中学生とは思えないイタズラだなあ。わんぱく小学生か」
ユーリ「ちょっとしたイタズラじゃん。すぐにつけたし」
僕「誰かじゃなくて、ユーリがやったのか!」
ユーリ「それはさておき」
僕「クイズの答えは?」
ユーリ「いやー……それがわかんないだよねー」
僕「どう考えた?」
ユーリ「こーゆーのって、直列と並列の問題だよね、って考えた」
僕「ふむふむ」
ユーリ「小学校の理科実験でやった。電池と、豆電球と、二つのスイッチがあって、直列につなぐか並列につなぐか……」
僕「図に描いてほしいな」
ユーリ「二つのスイッチをこんなふうに直列(ちょくれつ)につないだとしたら、 スイッチAがオンになってたら、スイッチBでつけたり消したりできるけど、 スイッチBがオフだったらダメ」
二つのスイッチを直列につないだ
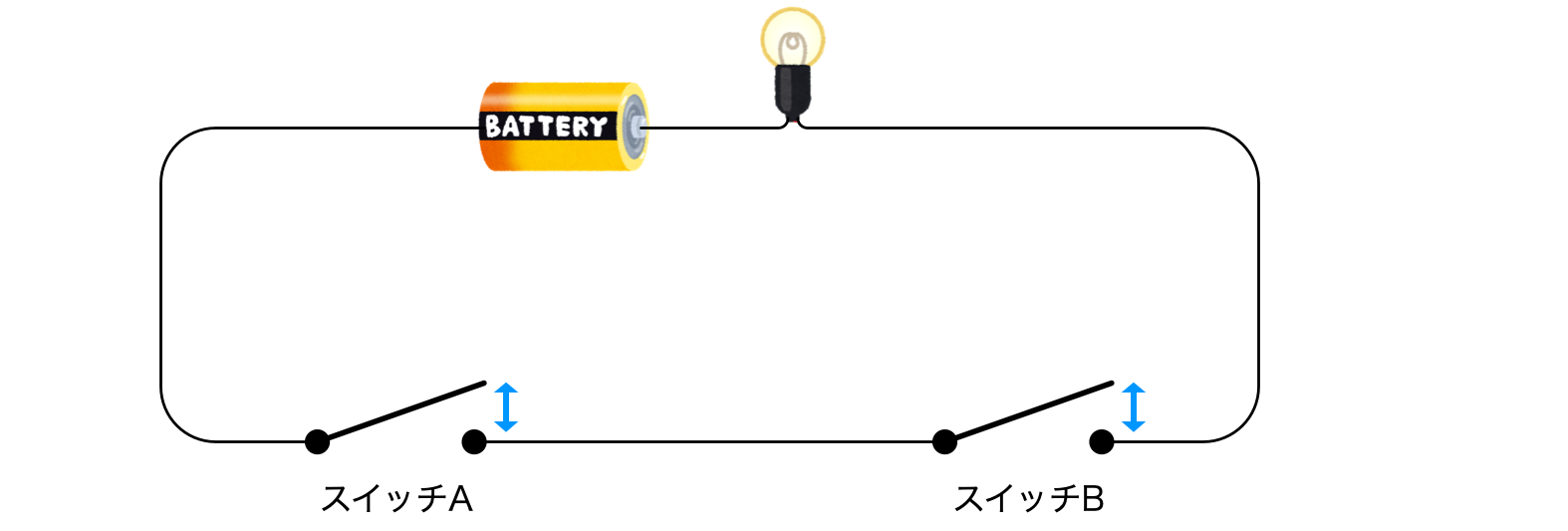
僕「そうだね」
スイッチAがオンのときには、スイッチBで点灯・消灯できる
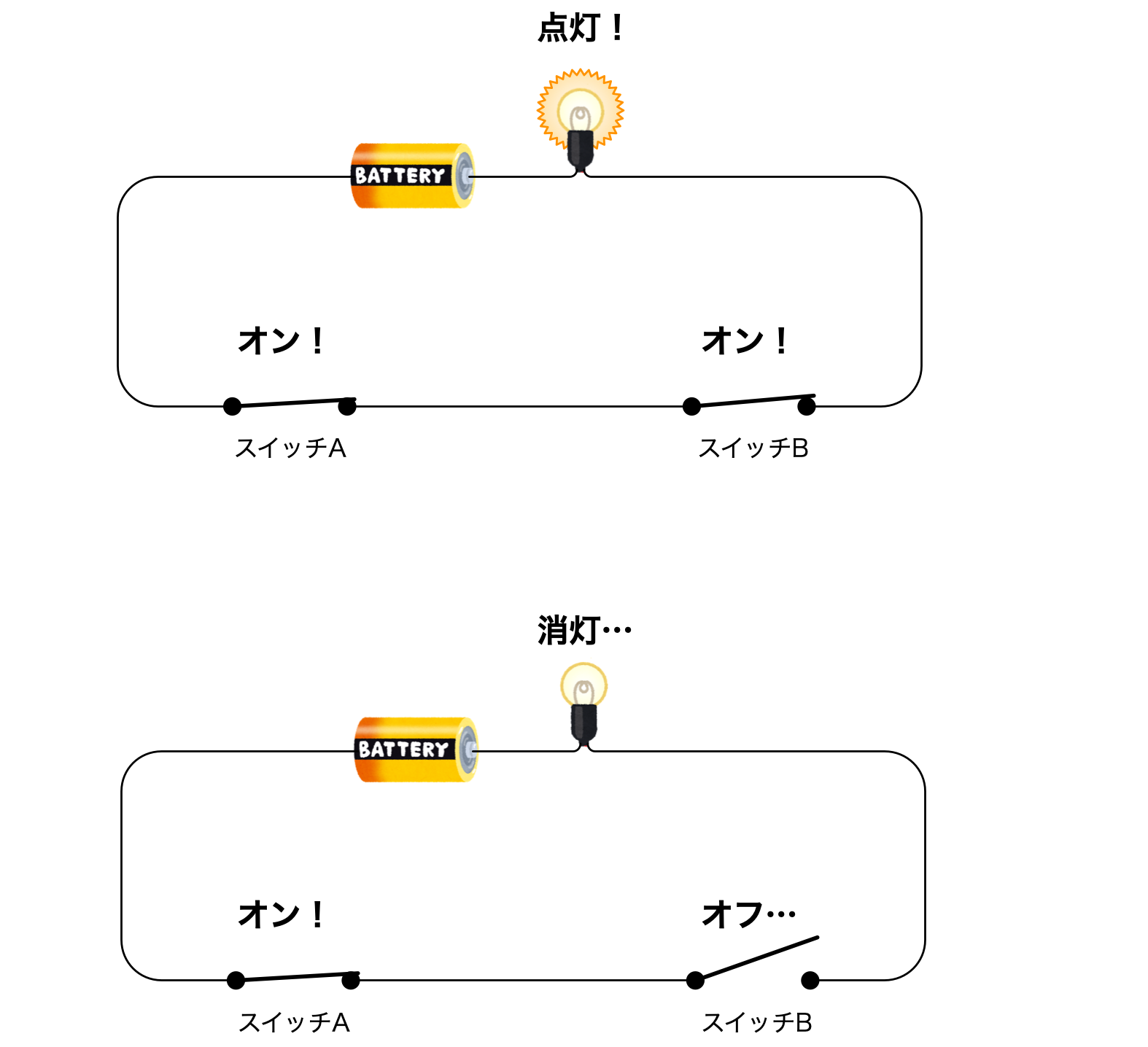
スイッチAがオフのときには、スイッチBでは点灯できない
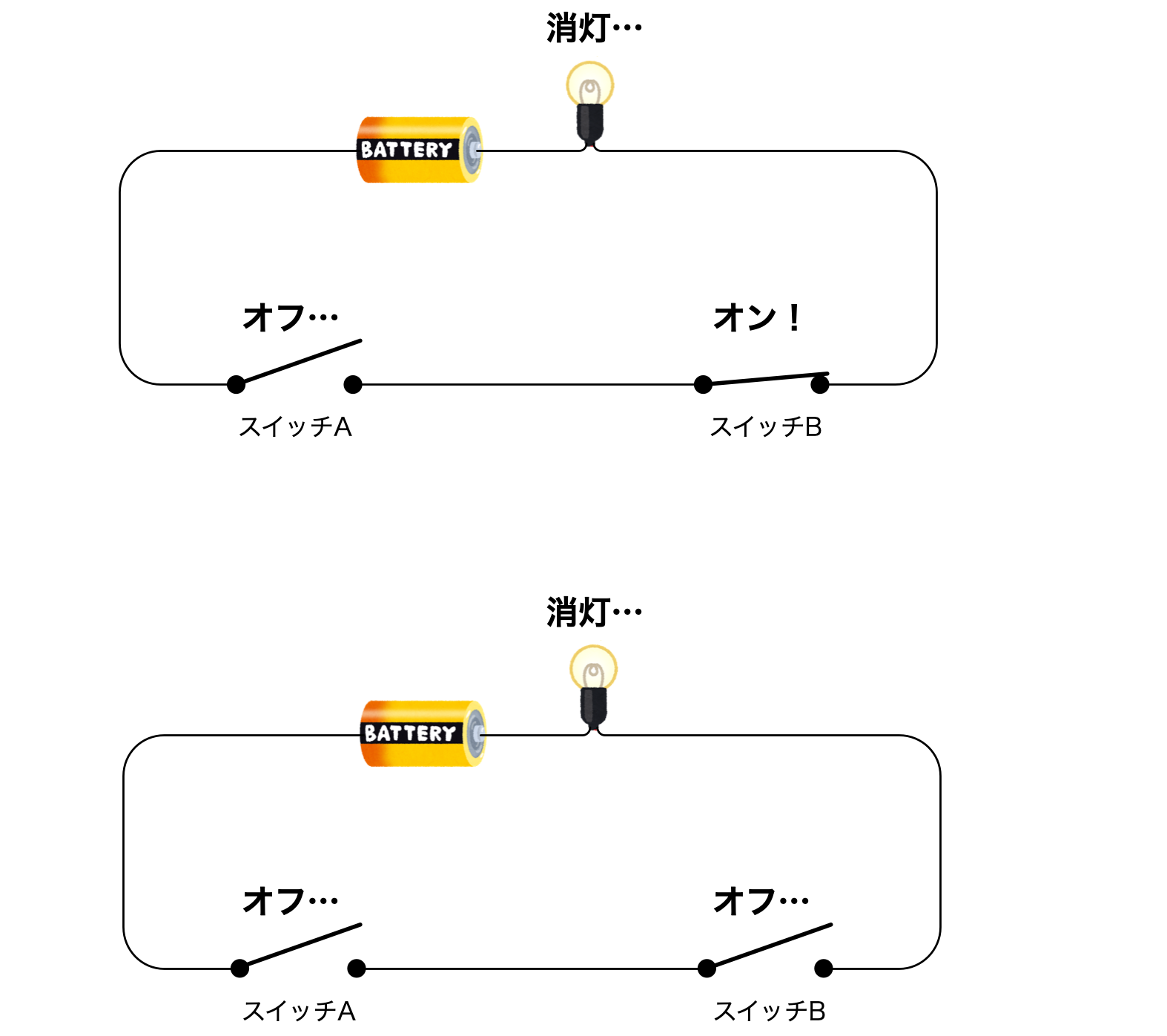
僕「同じことがスイッチBについてもいえる」
ユーリ「そゆこと。だから、直列はダメ。当たり前だけど、両方がオンになってないと点灯しないから。でも、並列でもダメなんだよー」
ユーリ「二つのスイッチを並列(へいれつ)につないだとしたら、 相手が消してたらうまくいくけど、つけてたらダメ」
二つのスイッチを並列につないだ
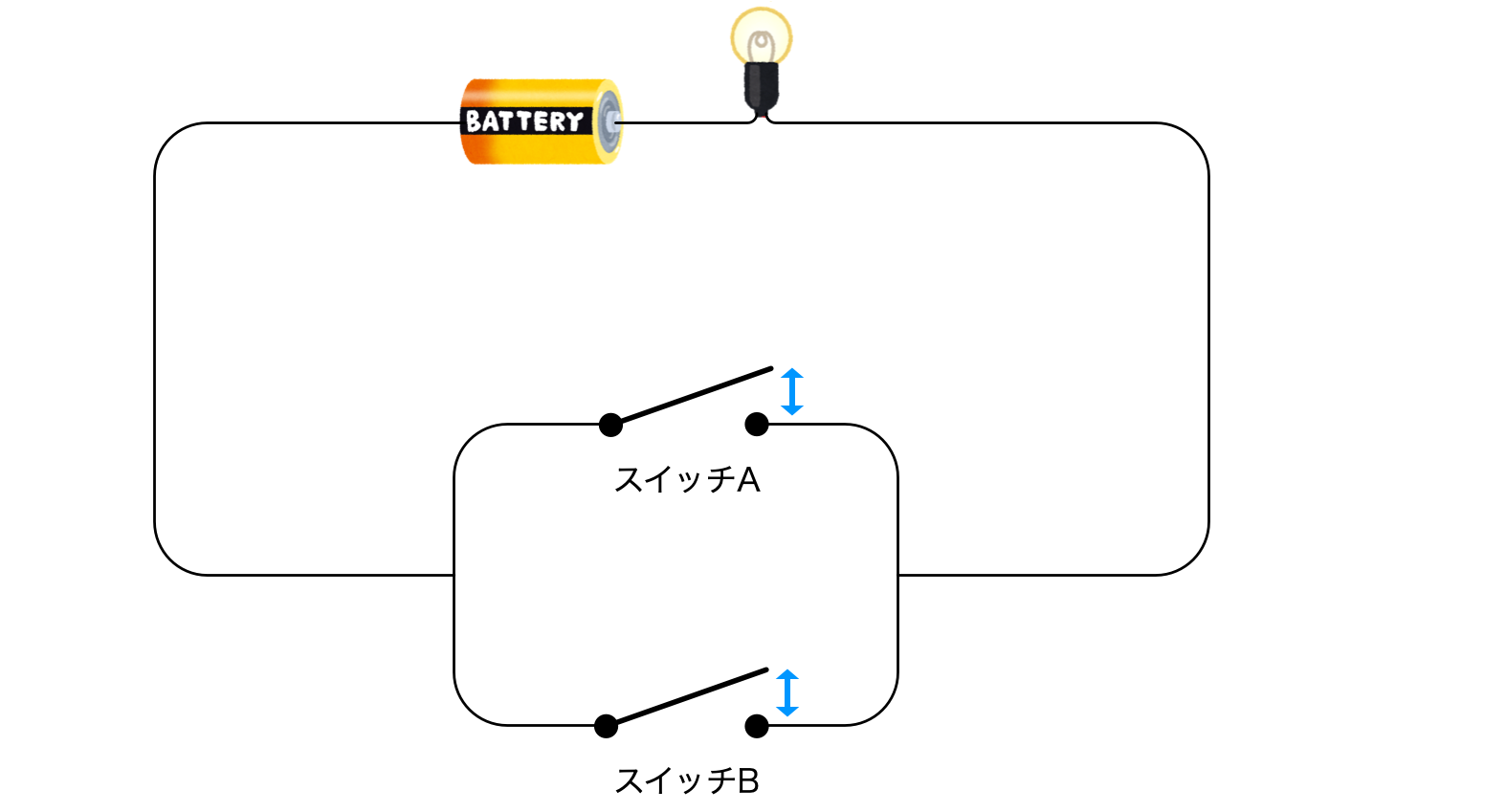
僕「これは、直列のときとそっくりだよね。スイッチを並列につないだときはこうなる」
スイッチAがオフのときには、スイッチBで消灯・点灯できる
スイッチAがオンのときには、スイッチBでは消灯できない
ユーリ「そっくりってゆーか、反対ってゆーか……」
僕「もちろん、スイッチBについてもいえる。つなぎ方はスイッチAとスイッチBで対称だから、当然だけど」
ユーリ「だから結局、直列でも並列でもダメ。このクイズのような配線なんてできんの? ……って、できるハズじゃん。実際にあるんだもん!」
僕「セルフツッコミ」
クイズ(電球の点灯・消灯、再掲)
階段の途中に電球が一つあります。
また、スイッチAとスイッチBの二つのスイッチがあります。
どちらのスイッチでも電球をつけること(点灯)ができ、 どちらのスイッチでも電球を消すこと(消灯)もできるようにしたいと思います。
どんなふうに配線したらいいでしょうか。

ユーリ「そんで? 答えは?」
僕「うん。三路スイッチという特殊なスイッチを使う方法がある」
ユーリ「さんろすいっち? さんろ?」
僕「数の「三」と道路の「路」で三路。こんなふうに一つのスイッチから三本の線がでていて、 そのうちの二本だけがいつもつながっている。 スイッチを切り換えると、つながる二本が変わるようになっている」
三路スイッチ
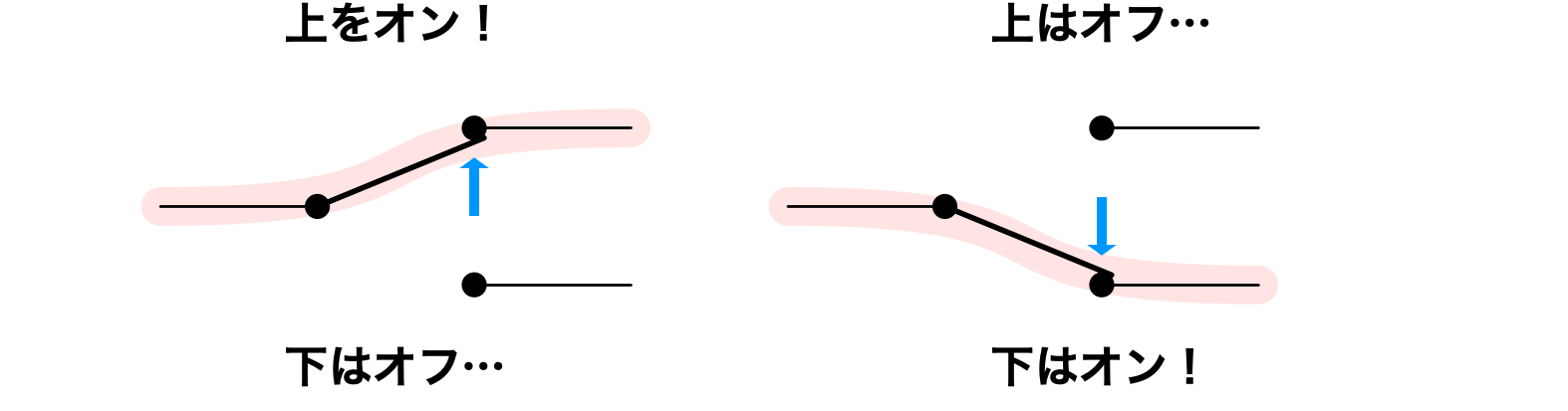
ユーリ「へー、こんなのあるんだ。上げると上につながって、下げると下につながる?」
僕「そうだね。スイッチAとスイッチBの両方ともこの三路スイッチにする。そして、全体としてこんな配線をするんだ。 そうすると、どちらのスイッチを使っても電球を点灯できるし、消灯できる。目的達成だ!」
クイズの解答
三路スイッチを使って、下図のような配線にする。
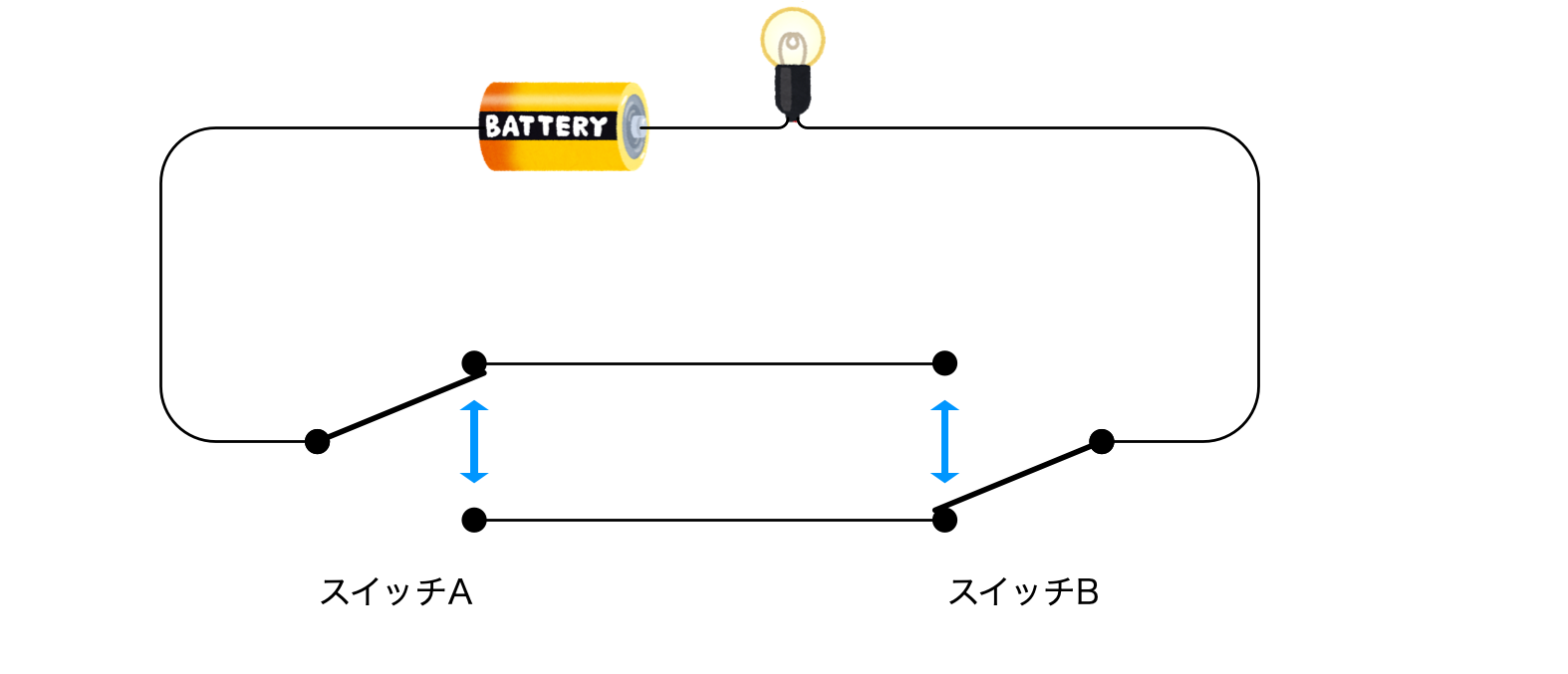
ユーリ「えーと? ほんとにうまくいく?」
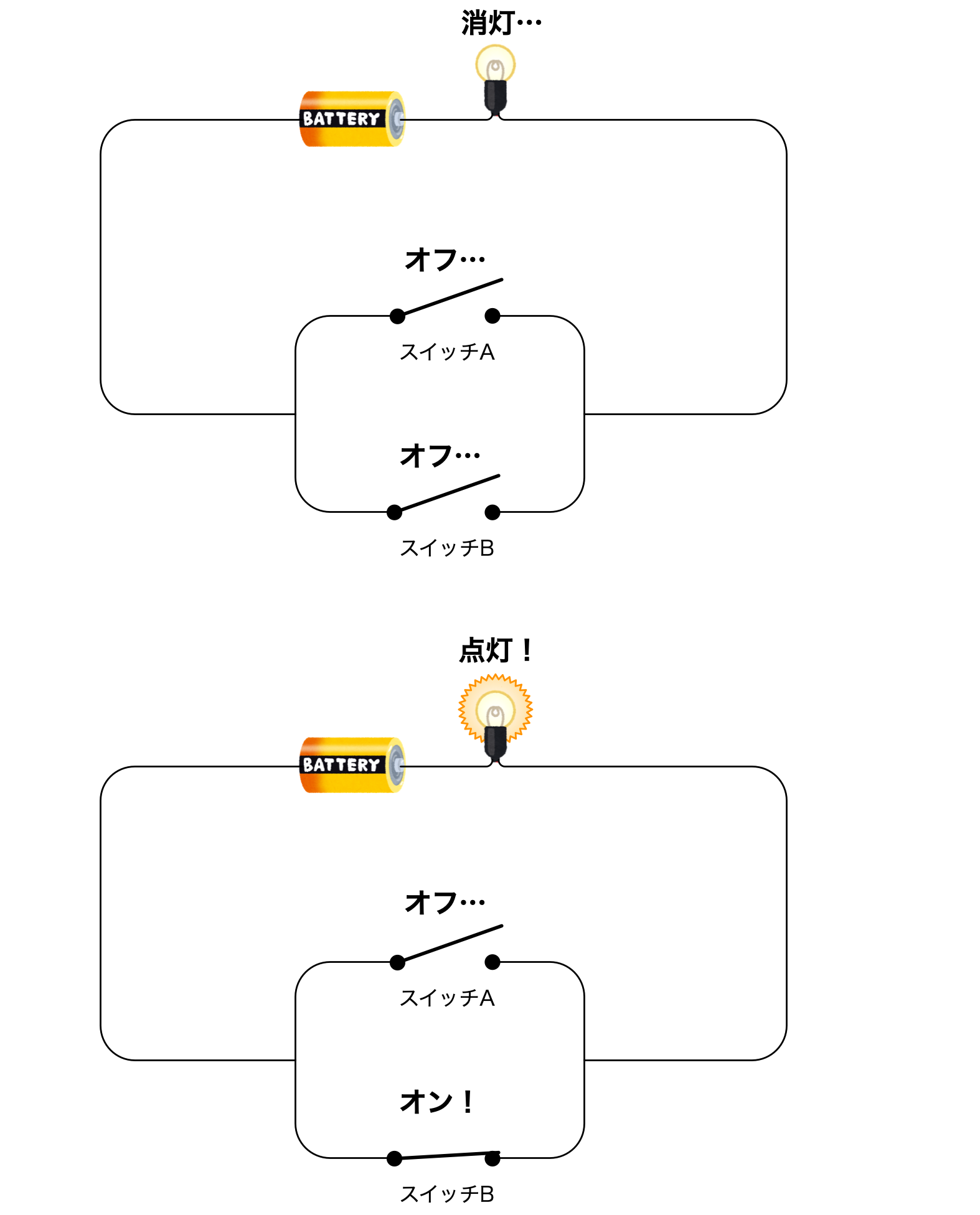
僕「うまくいくよ。実際にやってみよう。まず、スイッチAが上にあるとき、スイッチBを使って点灯・消灯できる」
スイッチAが上のとき、スイッチBで点灯・消灯できる
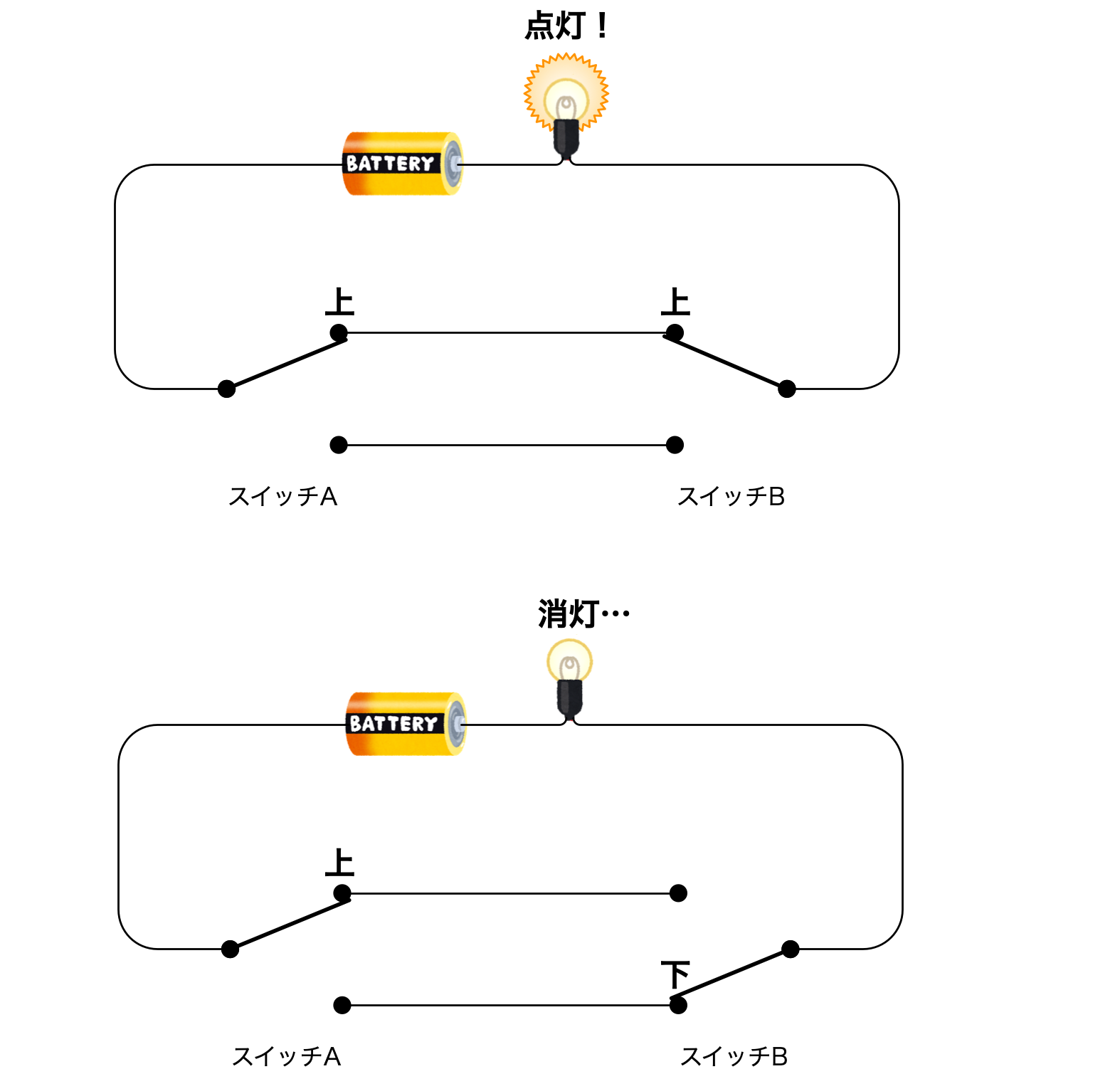
ユーリ「……」
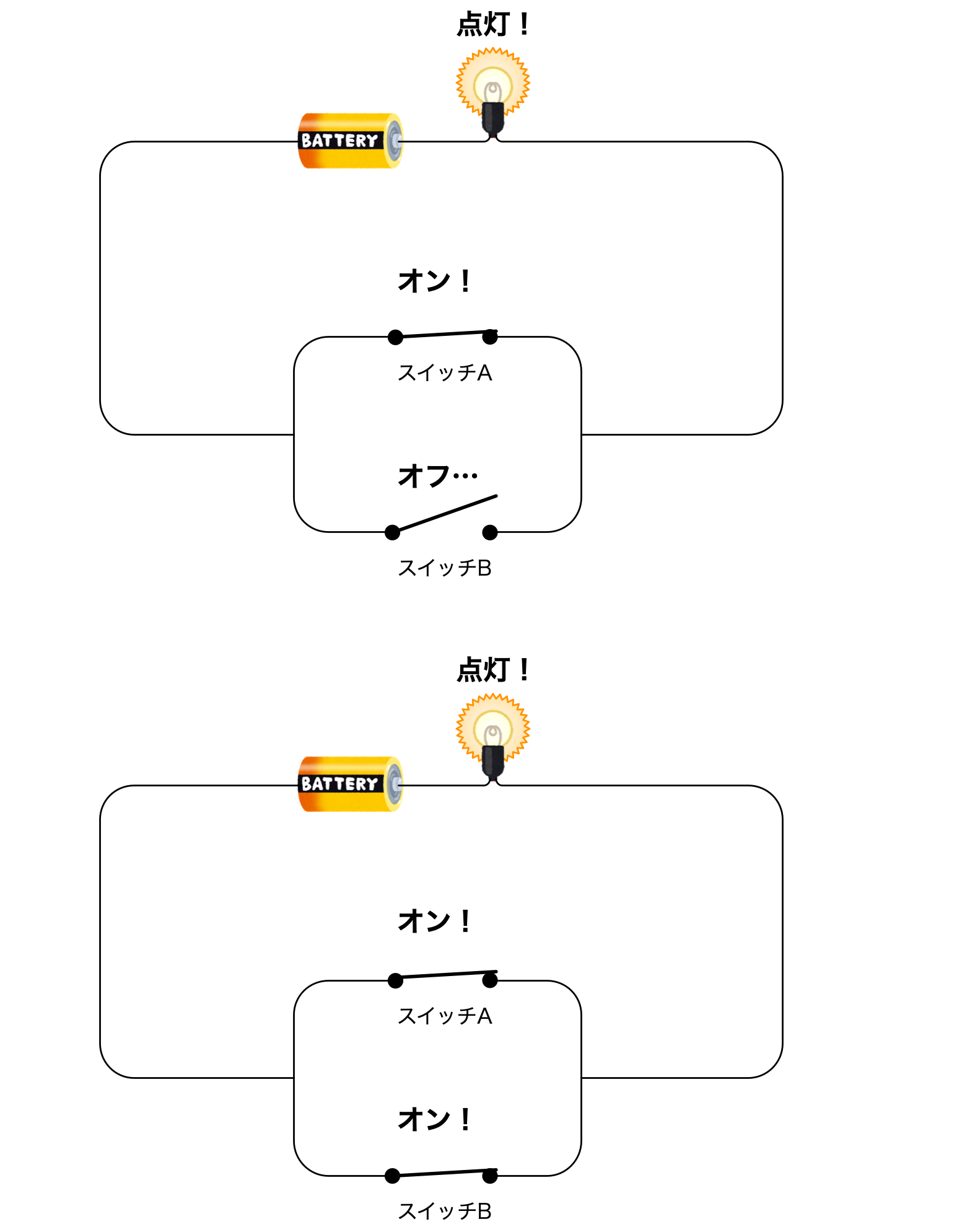
僕「そして、スイッチAが下にあるときでも、スイッチBを使って点灯・消灯できる」
スイッチAが下のとき、スイッチBで点灯・消灯できる
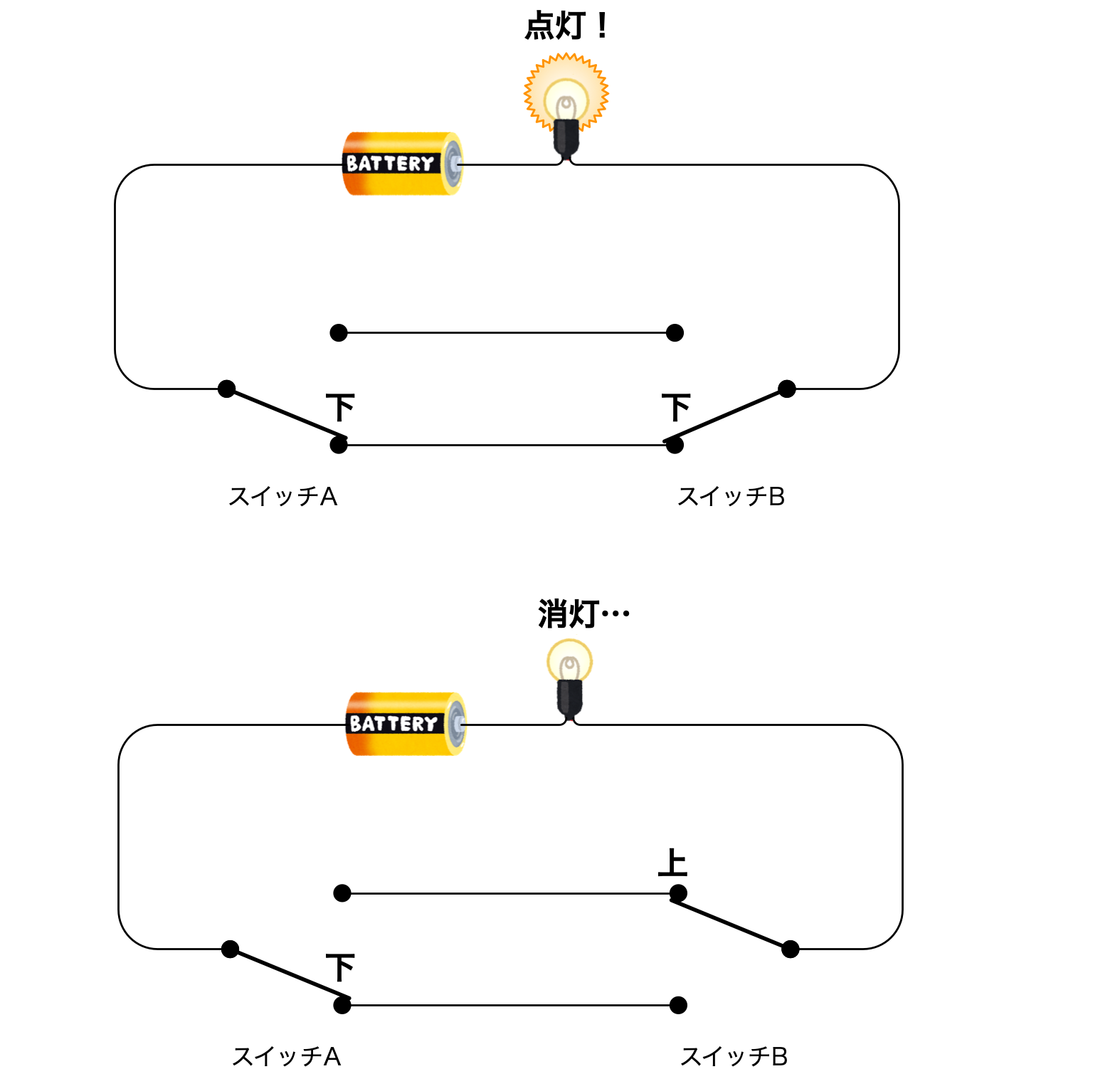
ユーリ「……」
僕「え、そんなに難しくないよね。ユーリなら見たらすぐにわかると思ったんだけど」
ユーリ「……」
ユーリは深い思考モードに入ったらしい。
問題を解くとき、ユーリはときどきこんなふうに無言になる。ふだんは軽口を飛ばしているけれど、 いったんハマると口を閉じ、外からの音も聞こえず、どっぷりと思考に浸るのだ。
その気持ちはとてもよくわかる。思考のためには沈黙が必要。思考のためには時間が必要なのだ。
もっとも、解答が提示されてから思考モードに入るのは珍しいことだ。
ユーリの中では彼女だけの世界が広がり、何かを考えているに違いない。 もちろんそれが何なのかは僕にはわからない。彼女が《こちら側》に戻ってきて、言葉にしてくれるまではわからない。
だから、僕は待つ。
思考モードに入ったユーリに話しかけたりせず、静かに待つのだ。
窓からの光を受けて金色に輝く、彼女の栗色の髪を眺めながら。
ユーリ「ねえお兄ちゃん!」
僕「お、戻ってきた。お帰り」
ユーリ「これって、二つの三路スイッチが……《同じ向きなら点灯》で《違う向きなら消灯》ってことだね!」
同じ向きなら点灯、違う向きなら消灯
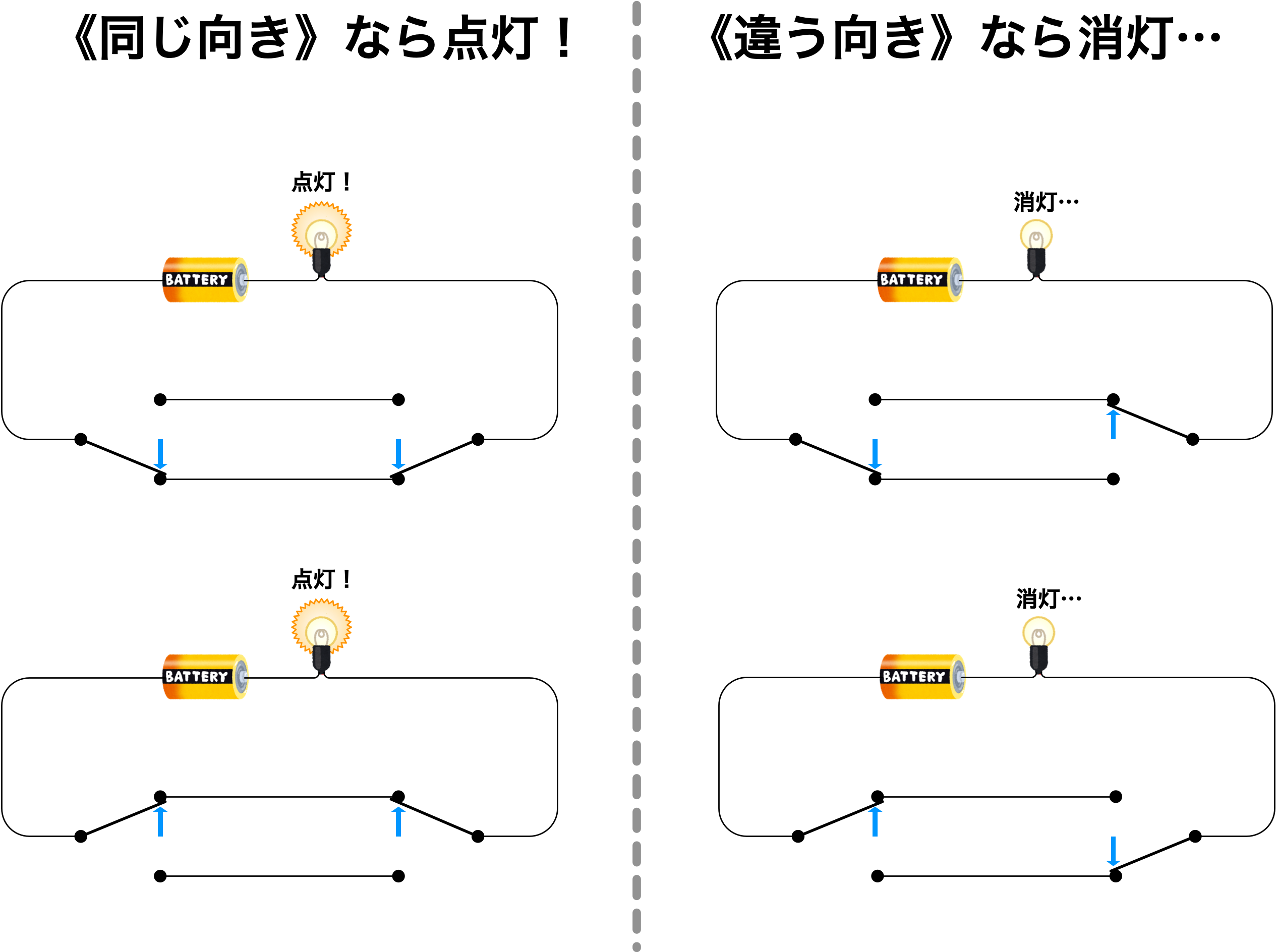
僕「うんうん、そうだね! ユーリの言う通りだ。そのことを考えてたの?」
ユーリ「そだよん。ごちゃごちゃして気持ち悪かったから、バシッとキメたかった。向きが同じかどうかで、点灯するかどうかが決まる!」
僕「まったくユーリの言う通り。スイッチAとBが同じ向きになっていたら電球は点灯する。 そしてスイッチAとBが違う向きになっていたら電球は消灯する。その通り!」
ユーリ「ふふん」
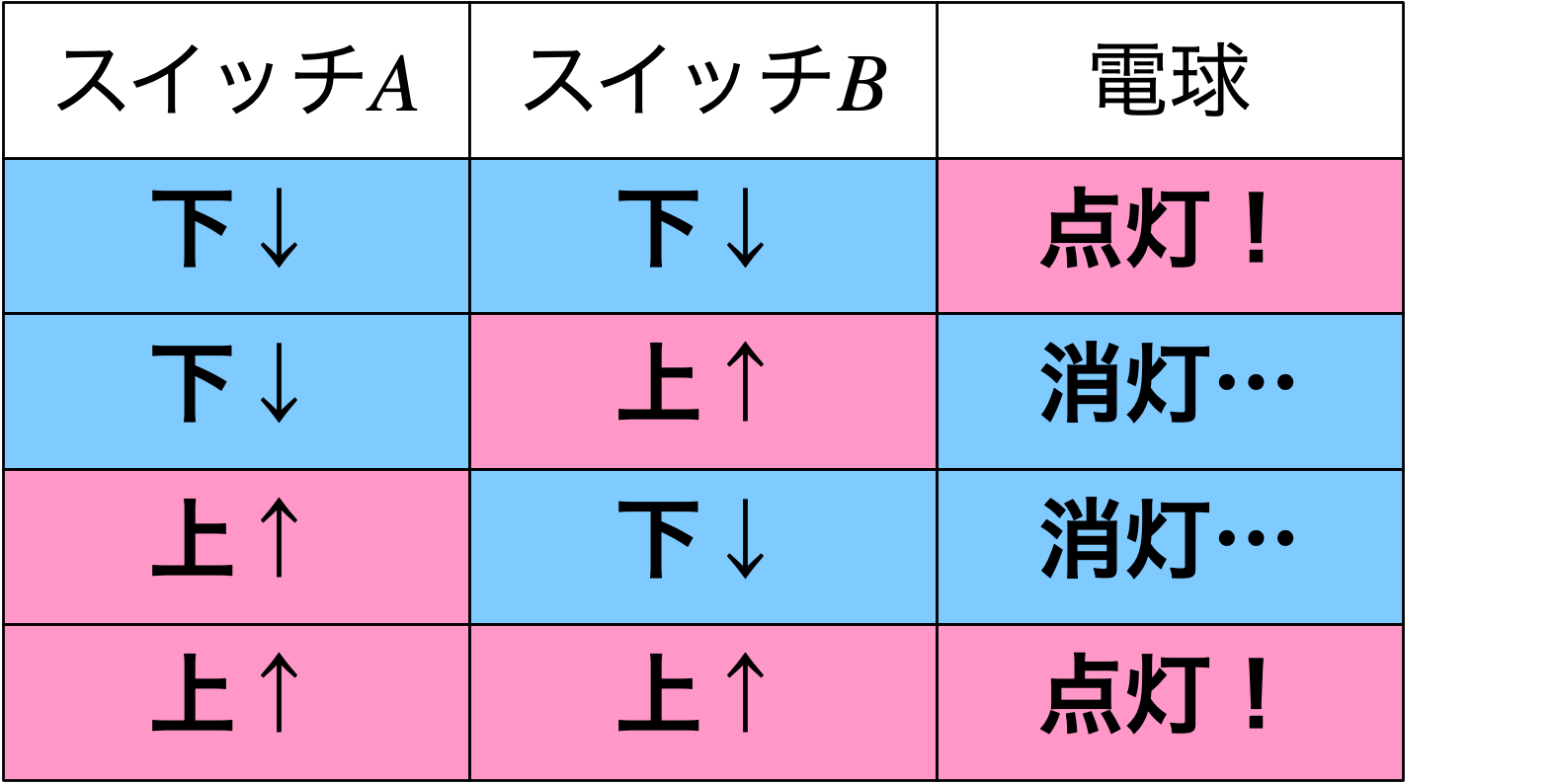
僕「端的にまとめたいなら、こんなふうに表にしてもいいね」
クイズの答えを表にまとめた
ユーリ「ほほー?」
僕「三路スイッチは《上》にするか《下》にするかの二通りある。 そして三路スイッチは二個ある。 だから、すべての場合は四通りになる」
ユーリ「ふんふん。そして、電球は《点灯》か《消灯》の二通り?」
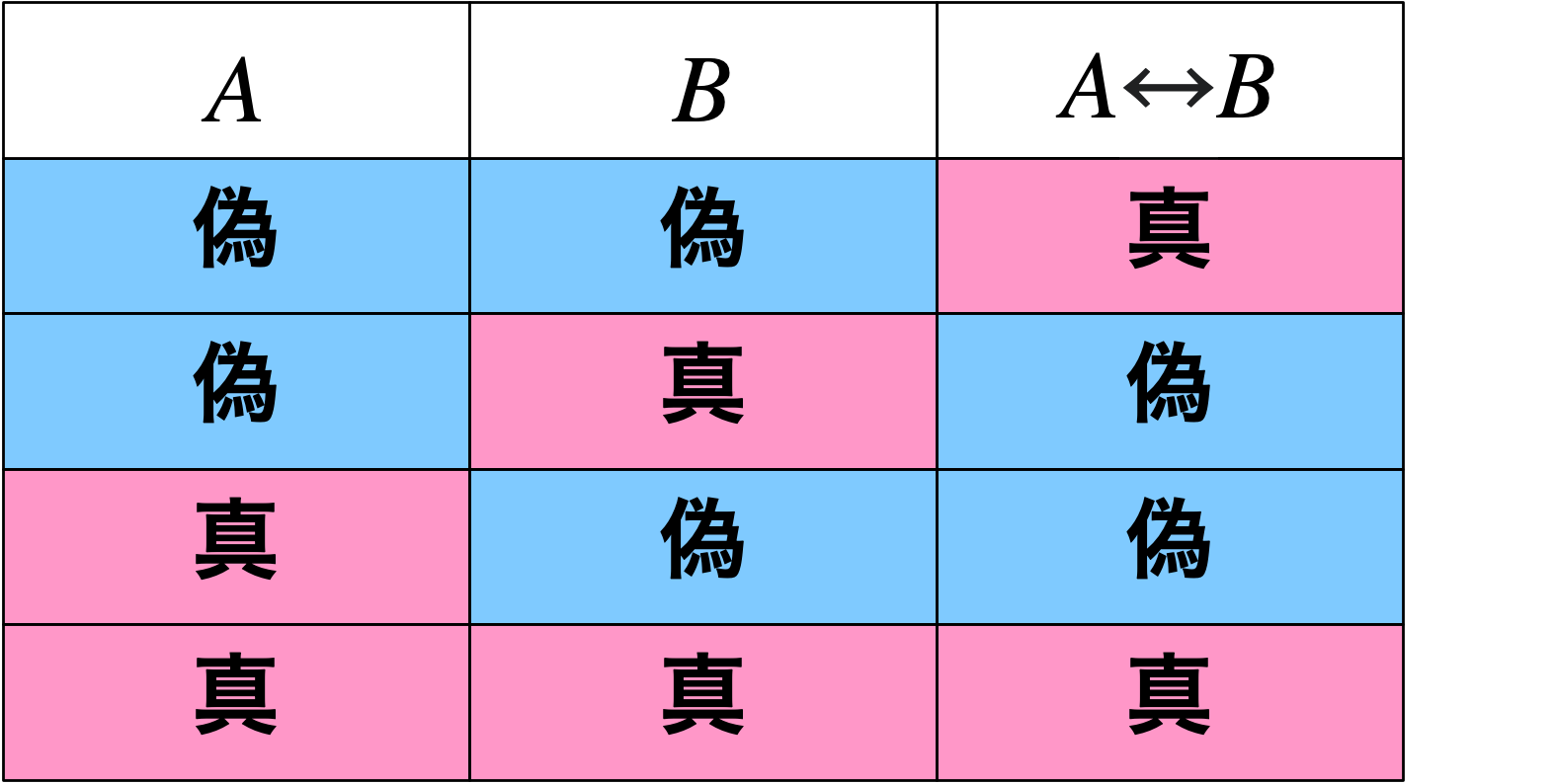
僕「そういうこと。そしてさらに、このパターンから、 《上》と《点灯》を真(しん)と見なして、《下》と《消灯》を偽(ぎ)と見なすと、 同値を表す論理演算の真理値表になってることがわかる!」
同値の真理値表
ユーリ「ユーリは二進法のイコールだと思ってた。0と1を比べるの」
二進法一桁を比較する
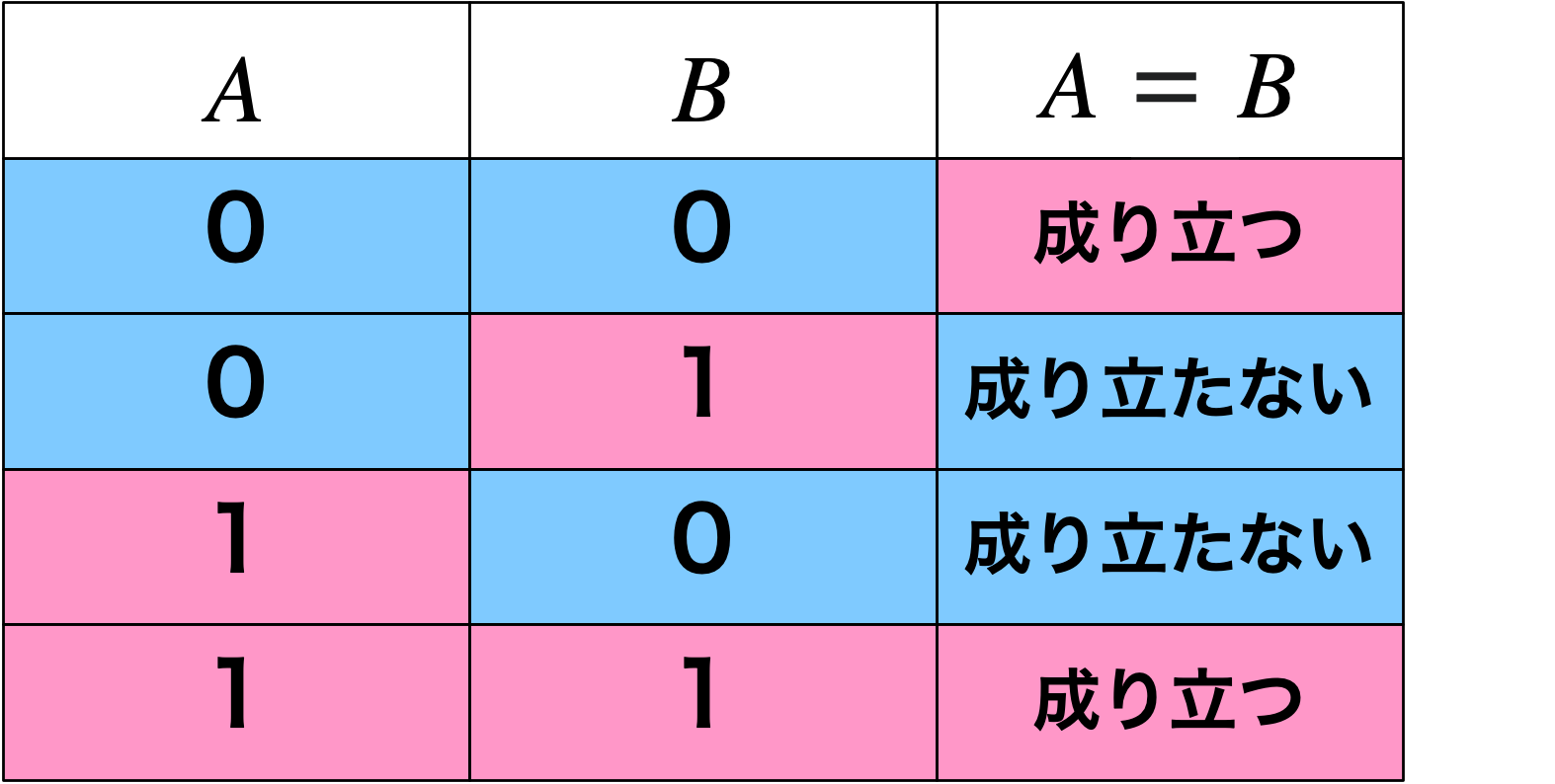
僕「なるほどね。これも同じパターンになってるね。そうかそうか! ユーリがさっき考えていた直列や並列も、 真理値表で表せる!」
ユーリ「お?」
僕「三路じゃない普通のスイッチで《オン》と《オフ》をそれぞれ真と偽で表して、《点灯》と《消灯》をそれぞれ真と偽で表すことにする。 そうすれば、直列は論理積(ろんりせき)の真理値表と同じパターンになる。《二つとも真のときだけ真になる》というのが論理積だから」
直列つなぎと論理積は同じパターン

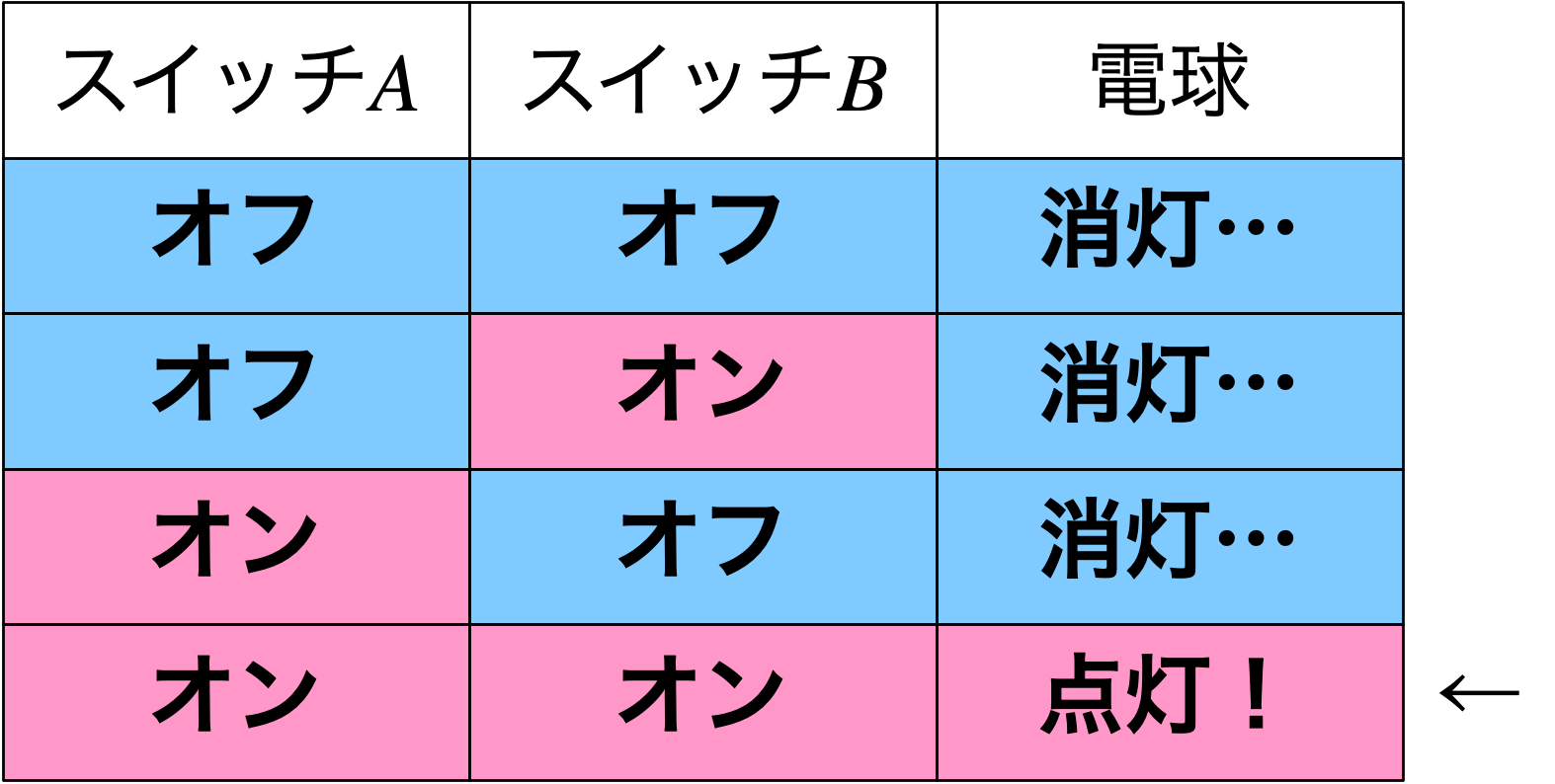
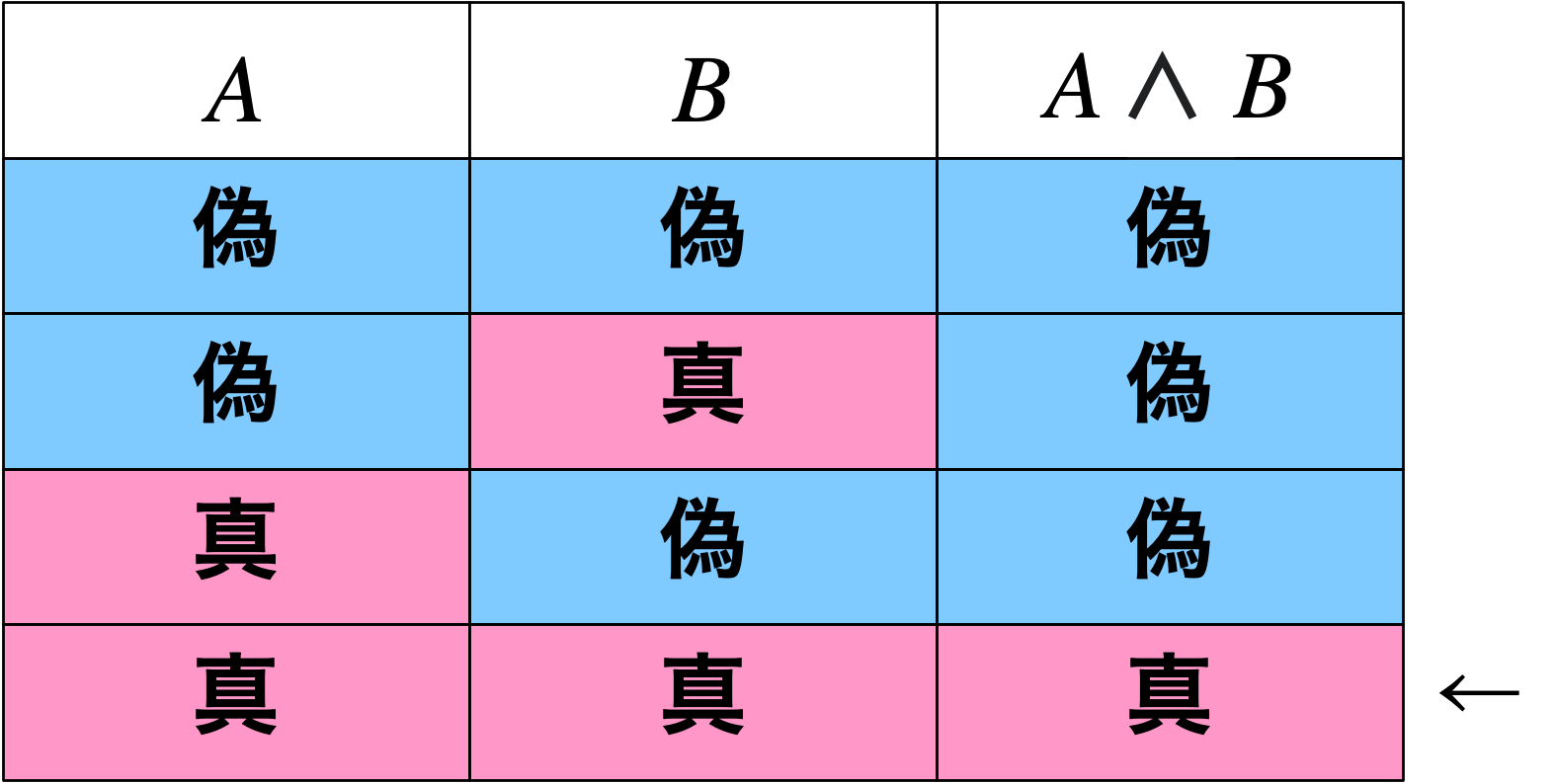
ユーリ「ははーん。だったら並列は……論理和、だっけ?」
僕「そういうことだね。《二つとも偽のときだけ偽になる》のが論理和(ろんりわ)だ」
並列つなぎと論理和は同じパターン

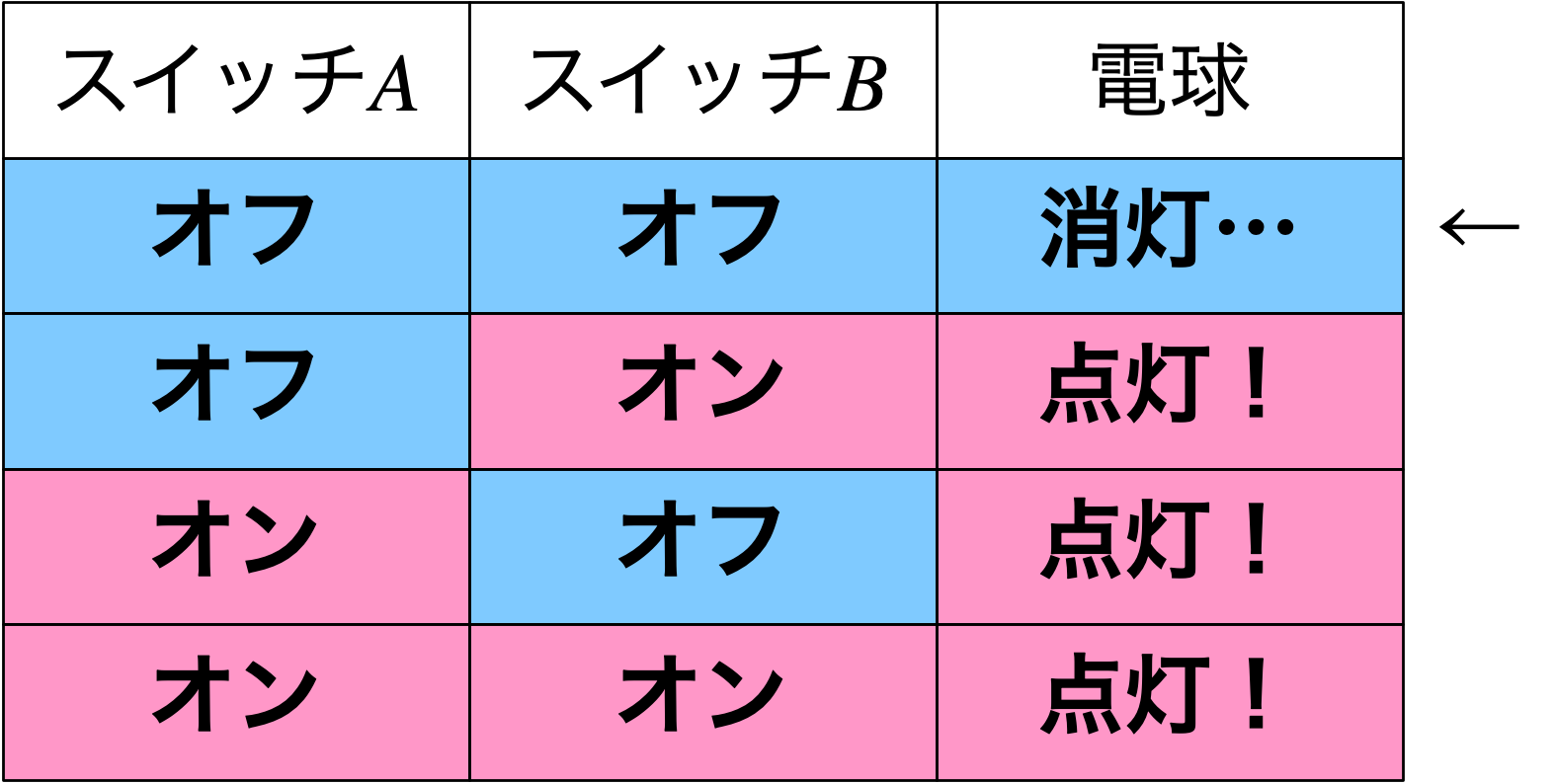
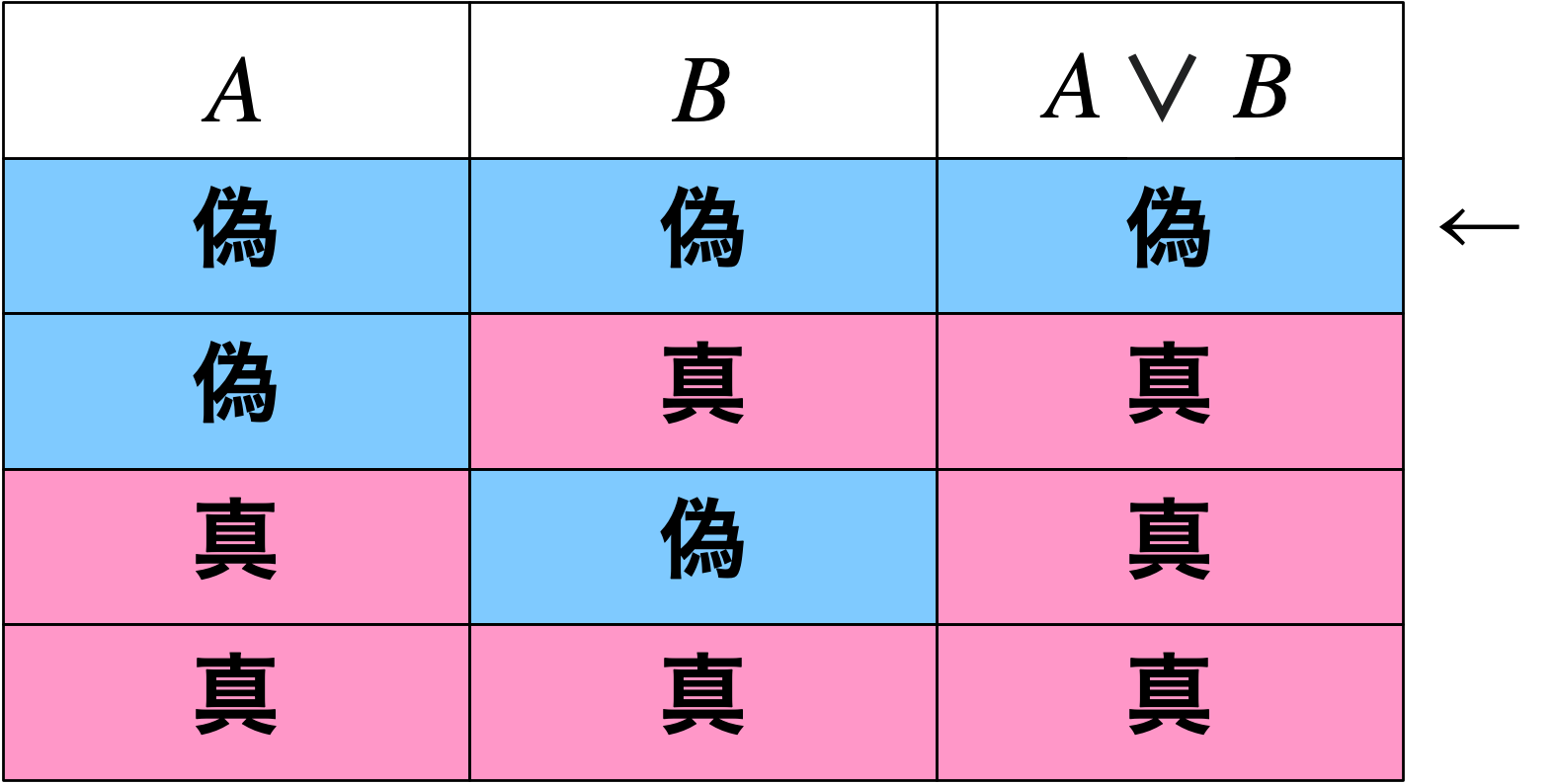
僕「うんうん。そうだそうだ。そうだよそうだよ!」
ユーリ「どしたん?」
僕「ほら、さっきユーリが直列と並列は反対だって言ってたよね」
ユーリ「うん。この表でもそーなってる」
僕「それって、ド・モルガンの法則になっているわけだ。反対というか双対(そうつい)だね」
ユーリ「そうつい?」
僕「《論理積の真理値表》に書いてある真と偽をごっそり交換すると、《論理和の真理値表》が得られる。 別の言い方をするなら、真と偽を交換して、論理積と論理和を交換しても、正しい真理値表になっている。 双対って、そういう関係のことだよ。論理積と論理和は無関係でバラバラなものじゃないんだね」
ド・モルガンの法則
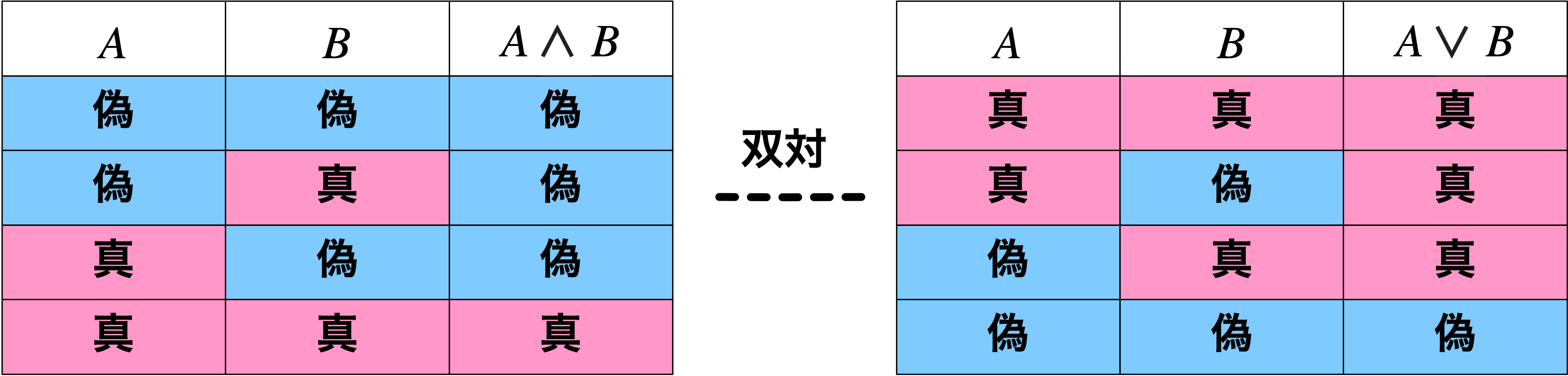
真と偽を交換して、論理積と論理和を交換しても、正しい真理値表になっている。
$$ \begin{align*} \lnot(A \land B) &= (\lnot A) \lor (\lnot B) \\ \lnot(A \lor B) &= (\lnot A) \land (\lnot B) \\ \end{align*} $$
ユーリ「おー!」
ユーリ「お兄ちゃんと話しているといつも数学の話になるよね」
僕「そうかな」
ユーリ「そーだよー。いまもそーじゃん。 電池に電球をつなぐ話って理科じゃん? でもいつのまにか数学とか論理の話になってる。 別にいいけどねー」
僕「理科で出てくる話だからといって、数学と関係ないわけじゃないよね。 どんなものでも、何かを整理して考えるとき、数学は役に立つ」
ユーリ「数式マニアだもんね」
僕「数式に限らないよ。さっきは表にまとめたし」
ユーリ「スイッチがどっち向きになっているかを真や偽で表したり?」
僕「そうだね。電球が付いているかどうかを真や偽で表したりね」
ユーリ「うん」
僕「真や偽といったけど、別に電球が点灯しているのが「正しい」という意味で「真」といってるんじゃない。 単に、二つのものに対応させているだけ。だから、スイッチがオンになっているのを偽にして、電球が点灯しているのを偽にしてもかまわないよ」
ユーリ「あっ、それをやったら論理積と論理和も入れ替わるね!」
僕「そうそう」
ユーリ「だよね! だって、直列は両方オンのときだけ点灯だから、両方偽のときだけ偽になるのは論理和だもん」
僕「そういうこと。 真偽の対応を逆にしたら、直列つなぎが論理和になるし、並列つなぎが論理積になるわけだ。 ユーリは飲み込みが早いなあ!」
ユーリ「ふふん」
僕「そういう対応付けは解釈ともいえるかも」
ユーリ「解釈?」
僕「うん。対応づけ、解釈づけ、意味づけ……何と呼んでもいいけど、僕たちが《見たもの》を何かに《見なす》ことができるかなって話」
ユーリ「何言ってるかわからん」
僕「いま僕たちがやってきた《直列や並列を真理値表で考える》って話だよ。 スイッチのオンとオフをそれぞれ真と偽と見なし、電球の点灯と消灯をそれぞれ真と偽と見なす。 そうすると、スイッチの直列つなぎは、論理積だと見なすことができる。《見なす》ことができる」
ユーリ「ふむふむ。《見なす》って話はわかった。そんで?」
僕「そんなふうに、いろんなものを《見なす》ことができるなら、 ぜんぜん違う世界みたいに思ってたものの中に、 同じパターンが見えてきて楽しいぞって話」
そうなんだ、と僕は思う。
同じパターンが見えてくる。
同じ構造が見えてくる。
そして……あの人が言った言葉を思い出す。
「構造を見抜く、心の目が必要なんだ」
ユーリ「……」
僕「直列つなぎと並列つなぎって、小学校の理科で習うよね。あのときものすごく悩んだのを覚えてるよ」
ユーリ「へ? お兄ちゃんが? 直列つなぎと並列つなぎなんて、何も難しくないじゃん」
僕「いや、もちろんどういうのが直列つなぎで、どういうのが並列つなぎかはわかるよ」
ユーリ「何を悩むんだろ」
僕「直列と並列の二つをペアにして教えるのはどうしてかなって思ったんだ。 まったく違うものに見えたからだね。 直列つなぎと並列つなぎを対にして教えてる理由がわからなくて悩んでた」
ユーリ「すごい悩みを持つ小学生!」
僕「いや、いま言ったみたいに整理できてはいなかったよ。もっと漠然と、もやもやっとしてた。どこか納得できなかったんだ」
ユーリ「直列と並列をペアにする理由……」
僕「でもね、中学時代に読んだ本の中に直列・並列の話とド・モルガンの法則の関係が書いてあったんだよ。 《かつ》と《または》が入れ替わる双対の話。 それで、ものすごく納得したんだ。ああ、確かにこの二つはペアになってるってね」
ユーリ「すごい納得をする中学生!」
僕「でも、さっきの入れ替えを考えたら、ユーリだってめっちゃ納得するよね。しない?」
ユーリ「する」
僕「だろ?」
ユーリ「んー、でもね、いくら《見なす》としても、やっぱり《線がつながっている》のと《線が切れている》のは、ぜんぜん違う感じがする。 だって、電球が点灯しているときに線を切ったら消灯しちゃうでしょ? そしたら、何回切っても消灯したまま。 これって入れ替わる?」
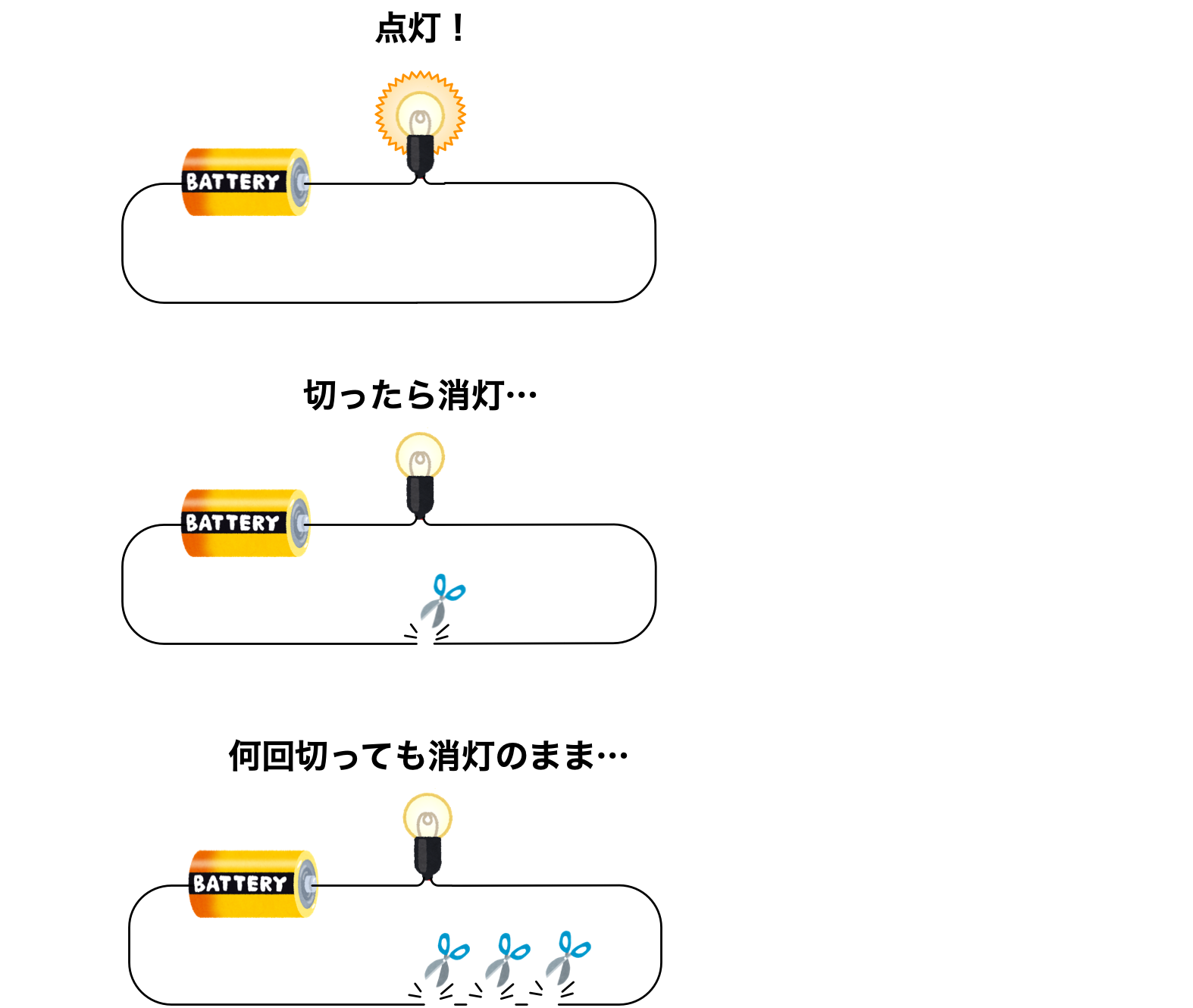
僕「それも双対を見抜く目で見れば、くるりと入れ替わるよ。 《つなぐ》と《切る》を交換すると同時に《点灯》と《消灯》も交換するんだ。 電球が消灯しているときに切れている線をつないだら点灯するし、何回つないでも点灯したまま!」
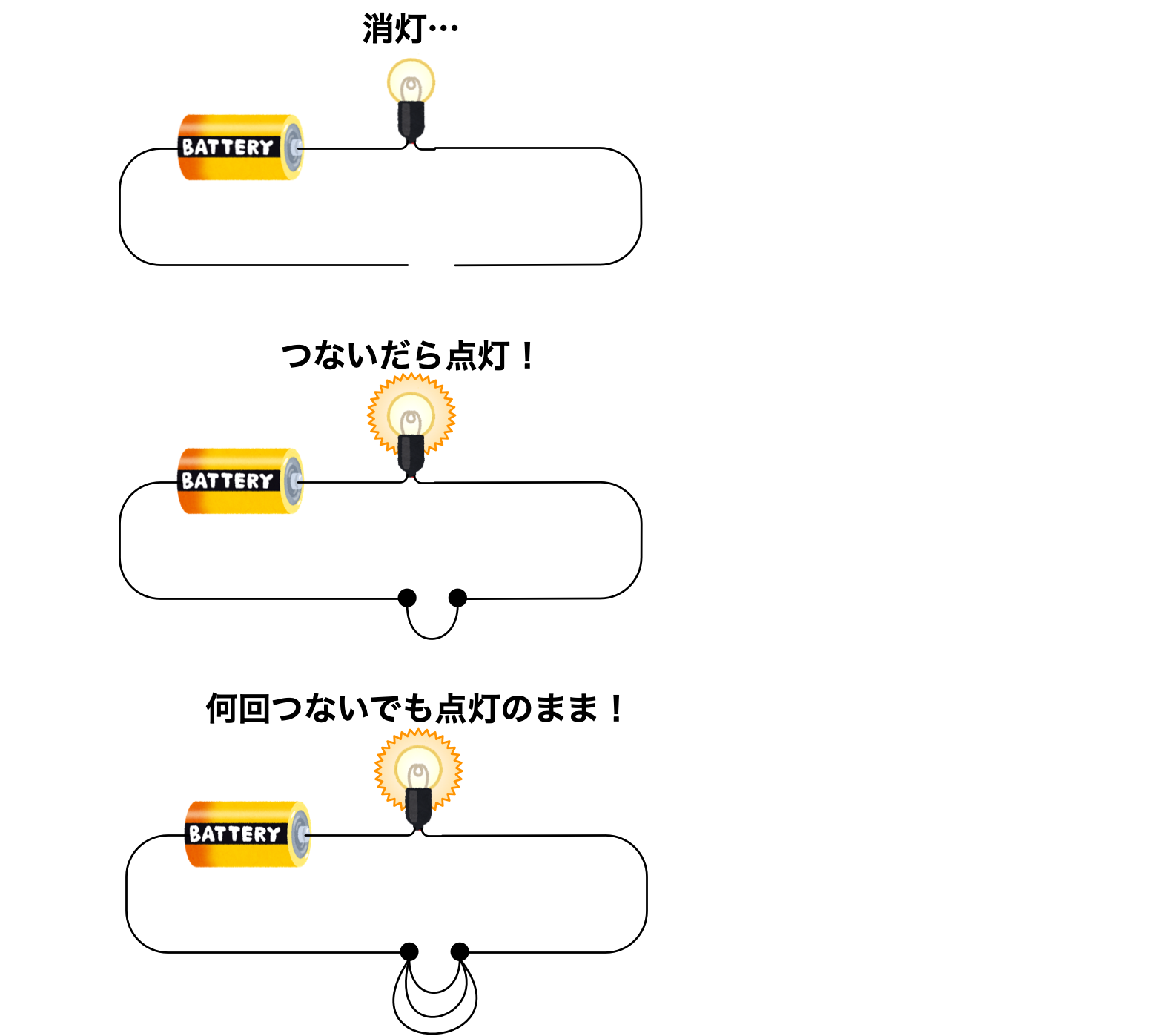
ユーリ「おっおっおっ。確かに!」
僕「直列と並列が双対になっているのは、もっと別のところにも出てくるよ。たとえば……」
※階段・スイッチ・電池・電球・ハサミのイラストは「いらすとや」さんから。
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第331回終わり)
(2021年8月20日)