![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
放課後。
いつものように僕は図書室に行くと、テトラちゃんがノートに何かを書きながらうなっていた。
僕「テトラちゃん、今日はどんな数学をやってるの?」
テトラ「あ、先輩……」
いつも元気なテトラちゃん、今日は反応がやや鈍いな。
僕「どうしたの、難しい数学に挑戦中?」
テトラ「い、いえ、そういうわけじゃないんですが……」
僕「テトラちゃんの歯切れがわるいのはめずらしいね。考えているところ邪魔しちゃったかなあ」
テトラ「難しい問題でもありませんし、そもそも数学でもないんです。いえ、数学になるんでしょうか……」
僕「もしよければ話を聞くよ。役に立てるかどうかわからないけど」
テトラ「ありがとうございます! 実はですね、先日双倉図書館(ならびくらとしょかん)で開かれた一般講座に参加したんですよ」
僕「そういえば、そんな話していたね。テーマは何だったの?」
テトラ「アルゴリズムです! 《リンクとストラクチャー》という副題が付いていて、 いろんなアルゴリズムのお話を聞いてきました。盛りだくさん過ぎてちょっと消化不良ですが……」
テトラちゃんはそういってお腹を撫でた。
学んだこと、お腹に入るんだろうか。
僕「おもしろかった?」
テトラ「はい。おもしろかったんですが、あとから配付資料を読み返してみると、 あちこちに『自分は理解していないな』と思うことが見つかったんです。 それから、何というんでしょうか……全体的にもやもやっとしていることもあります。 いえ、何をやってるかははっきりわかるんですよ。そんなに難しい話ではありませんでしたから。 でも、改めて考えると、何をやってるかがはっきりしなくなるんです。 だから、難しくて……」
僕「はっきりわかるけれど、はっきりしなくなる。 難しくはないけど、難しい。 それじゃ確かに……はっきりしなくて難しいね!」
テトラ「はい……わけがわからない悩みですみません」
そのとき僕は、ちょっとしたアイディアを思いついた。
僕「うん、だったらね、テトラちゃんが講義をするっていうのはどう?」
テトラ「あ、あたしが……講義? どういうことでしょう」
僕「テトラちゃんは一般講座に出席していろいろ学んできたわけだよね。 だから、その成果を僕に講義するんだ」
テトラ「あたしが……先輩に講義する」
僕「そうそう。いまの段階だとテトラちゃんの方がずっとわかっているはずだけど、 テトラちゃんが講義をして教えてくれるなら、僕もその理解に近付けてうれしい。 そして、もしかしたらテトラちゃんの「もやもや」がどこにあるのかを一緒に考えられるかもしれないよね!」
テトラ「先輩に教わるのではなく、先輩に教える……あたしが?」
僕「よろしくお願いします。テトラ先生!」
テトラ「わ、わかりました。けれど、何日か準備させてください……」
テトラちゃんのアルゴリズム講義は、一週間後に始まることになった。
一週間後。
テトラ「そ、それではお話します」
僕「よろしくお願いします」
テトラ「まずですね。あたし、先輩にすごく感謝しています!」
僕「え? まだ何にも話してないのに?」
テトラ「あたし《先輩に講義する》というつもりで準備をしていたんですが、 そうしたら、不思議なことがたくさん起きたからです」
僕「へえ……」
テトラ「配付資料を読むときに《書かれている内容を理解しよう》という気持ちだけじゃなくて、 《書かれている内容を理解した上で、先輩にちゃんと説明できるようにしよう》という気持ちになりました。 そうすると、不思議なことに、自分が何をわかっていないかがはっきりしてきたんですよ」
僕「それはおもしろいね! ああ、でも、それは納得いく話だなあ」
テトラ「えっ?」
僕「ほら、僕たちはよく数学の話をするよね。 そのときに相手に伝わるように説明しようとする。 でもなかなかうまくいかないし、伝わらないこともある」
テトラ「はい……」
僕「できるだけはっきり説明しようと思うと、 自分自身の理解があやふやなところが浮き彫りになること、あるねえ」
テトラ「そうなんですか、先輩も?」
僕「うん。テトラちゃんが放つ《根源的な質問》もすごく助かる。 それに答えることで、自分の理解が試されている感じがするんだ」
テトラ「あ、あたしは理解が遅いので……でも、そういっていただけるのはうれしいです」
僕「じゃあ、テトラちゃんの……テトラ先生の講義を聴くよ」
テトラ「双倉図書館の一般講座で学んだことを、あたしなりにまとめたので、 その順番でお話しします」
僕「うん。すごく楽しみだよ!」
テトラ「まずこちら、List 1のアルゴリズムを見てください」
List 1
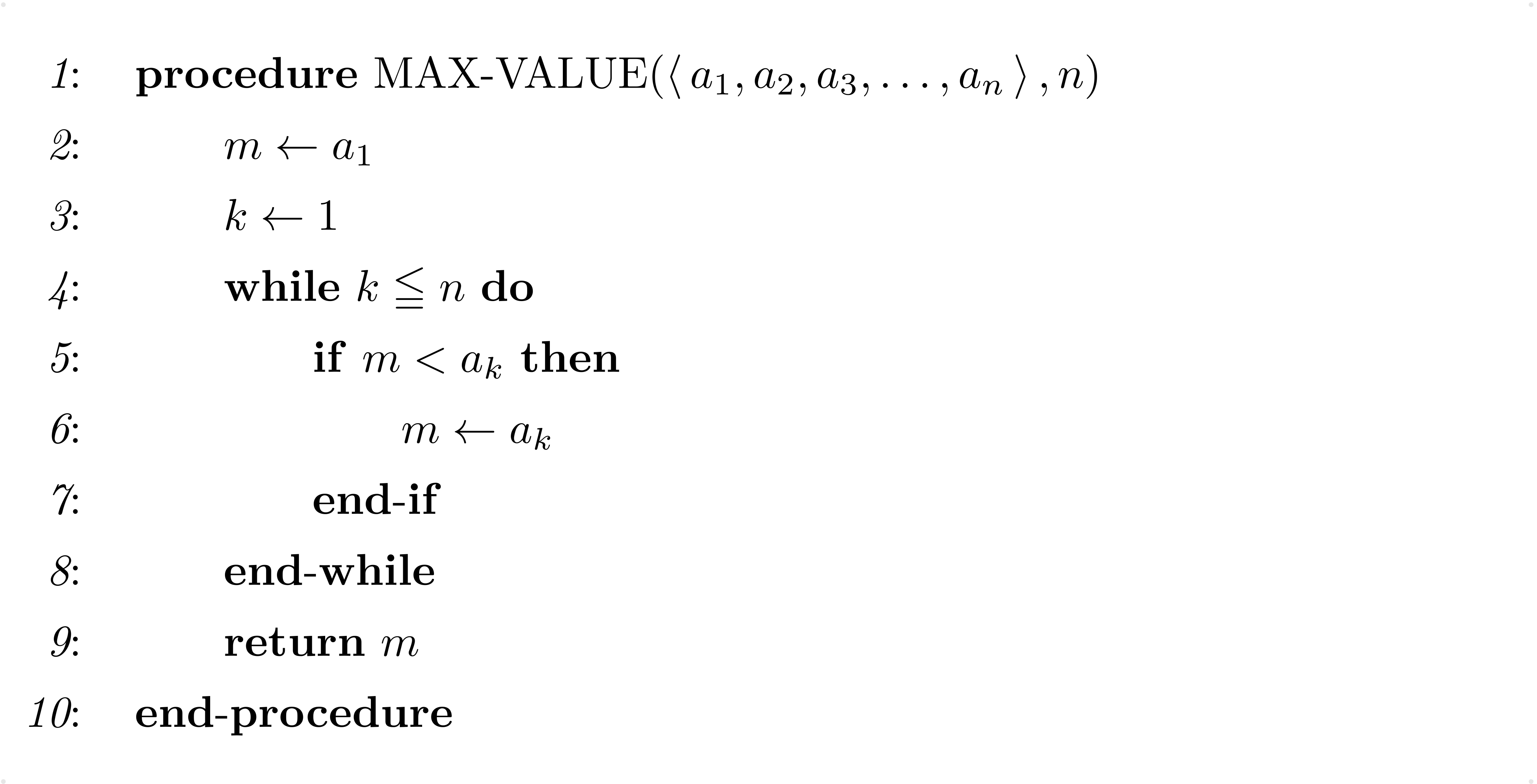
僕はテトラちゃんが提示したMAX-VALUEというアルゴリズムをざっと眺めた。
ああ、これはきっと、 $$ \LLRR{a_1,a_2,a_3,\ldots,a_n} $$ で与えられた数列の中から最も大きな数を見つけ出すんだろうな。
whileからend-whileまでの繰り返しで、 $m < a_k$ という比較を行っている。
きっと最大値が $m$ に代入されるんだろう。
僕「なるほど。List 1は僕にも理解できるよ。最大値を求めるアルゴリズムだね」
テトラ「はい。あたしもそう考えたんですが、あさはかでした」
僕「あさはか?」
テトラ「あたしは、書かれたものをちゃんと読まなかったんです。 確かにこのアルゴリズムは、 $a_1,a_2,a_3,\ldots,a_n$ という数列が与えられたときに、 要素の最大値を求めるものなんですが、重大な誤りがあるんです!」
僕「重大な誤り……」
テトラ「はい。重大な誤りです」
僕はちょっと焦った。
確かに僕も、List 1の内容をろくに読まずに口を開いてしまった。 あさはかだった。《重大な誤り》とは何だろう……

僕「……ああ、わかったよ。これじゃkの値はずっと1のままだ。増えていかないね」
テトラ「はい、そうなんです。kの値はずっと1のままですから、4行目の、 $$ k \LEQ n $$ という条件はいつまでも成り立ちます。つまりList 1のアルゴリズムは無限ループに入ってしまうことになります! その《重大な誤り》を修正したものがこちらのList 2になります」
List 2
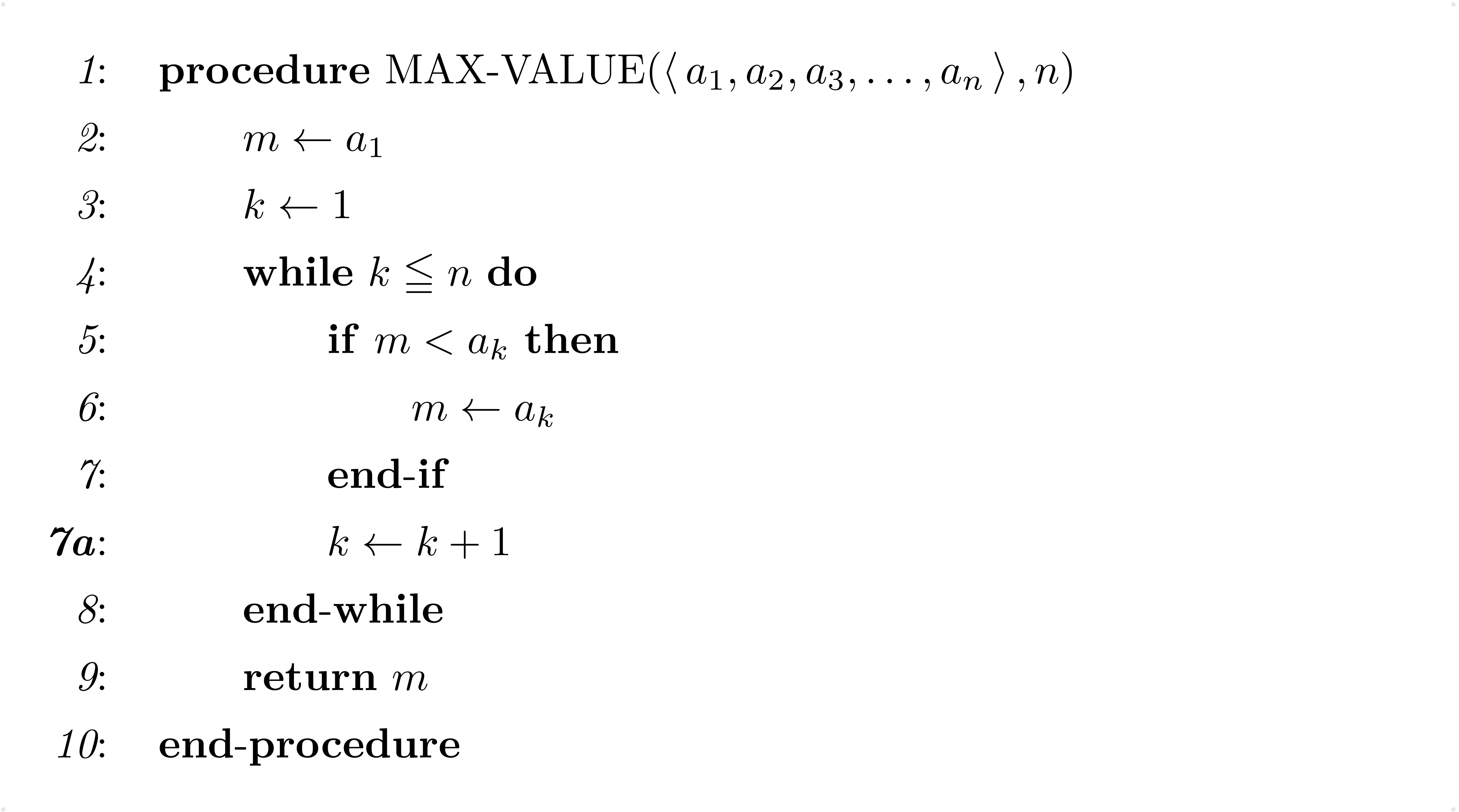
僕「そうだね。List 2では7aの行でkを増やしている」
テトラ「講師の先生から、やんわりと注意がありました。 アルゴリズムはパパッと読んでパパッと理解しようと考えないこと、だそうです」
僕「確かに……」
テトラ「では、仕切り直して、お話を始めます。 List 2は、 $$ \LLRR{a_1,a_2,a_3,\ldots,a_n} $$ という数列と、要素数 $n$ が与えられたとして、 最大値を求めるアルゴリズムです。 やっていることの概略はこうです」
僕「うんうん、そうだね。特に気になるところはないよ」
テトラ「え?」
僕「え?」
テトラ「あたしは一つ気になりました。これは《無駄な比較》をしていますよね?」
僕「無駄な比較って? ……ああ、ほんとだね! 最初の比較のこと?」
テトラ「はい、そうです。 $k = 1$ の時点、List 2の5行目で $$ m < a_k $$ の比較をするとき、 $$ m = a_1 $$ であることは最初からわかっています。 だって、2行目で代入したばかりですから!」
僕「確かにね……テトラちゃんはそれに気付いてたんだ」
テトラ「はい。手を挙げて講師の先生に質問しました。 kの値は2から始まってもいいですか……と。 そうしたら『よく気がつきましたね』と褒めていただきました!」
僕「……」
テトラ「ですから、List 3のようにすれば、比較の回数を減らすことができます。1回分だけですけれど」
List 3
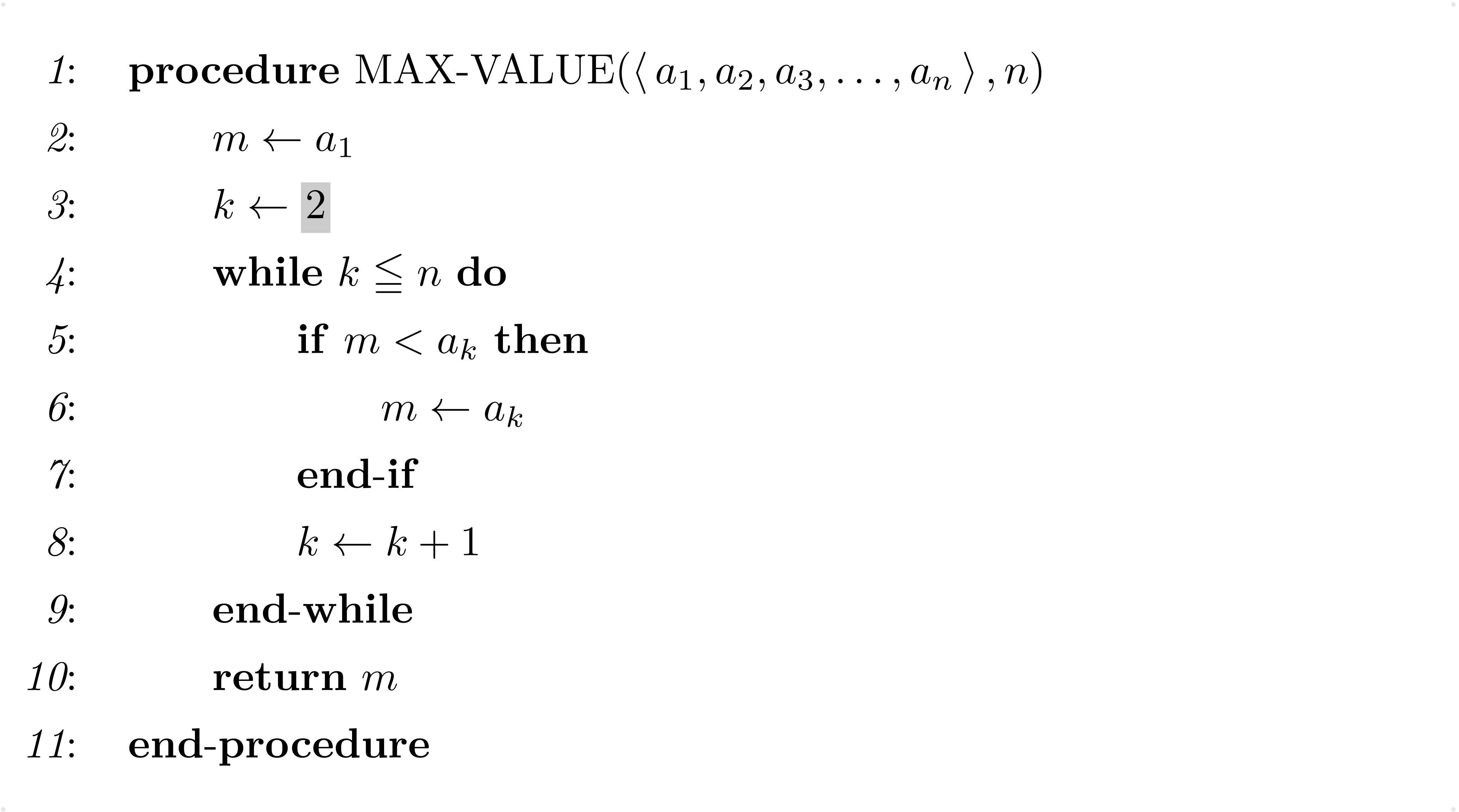
僕「なるほど、確かにそうだね。 うん、テトラちゃん。僕はちょっと《反省》してるよ」
テトラ「えっ?」
僕「僕は、どこか先輩気取りでいて、どこか気が緩んでいたみたいだよ。 もっと真剣に取り組むべきだったね。ごめん」
テトラ「そ、そんなことおっしゃらないでください! こうやって、 聞いていただけるだけでありがたいんですから……そ、 それでですね。最大値を求める話は、ここから始まるんです。 このアルゴリズムをどのように実装するか、です」
僕「実装?」
テトラ「はい。今回の講座では、 アルゴリズムがどのようなものかというお話から一歩進んで、 データ構造というものにも触れていました」
僕「データ構造……」
テトラ「data structureです。その最も簡単なものが配列です。 配列というものを使って数列を表現し、 先ほどの最大値を求めるアルゴリズムを実装した擬似コードがList 4です」
List 4
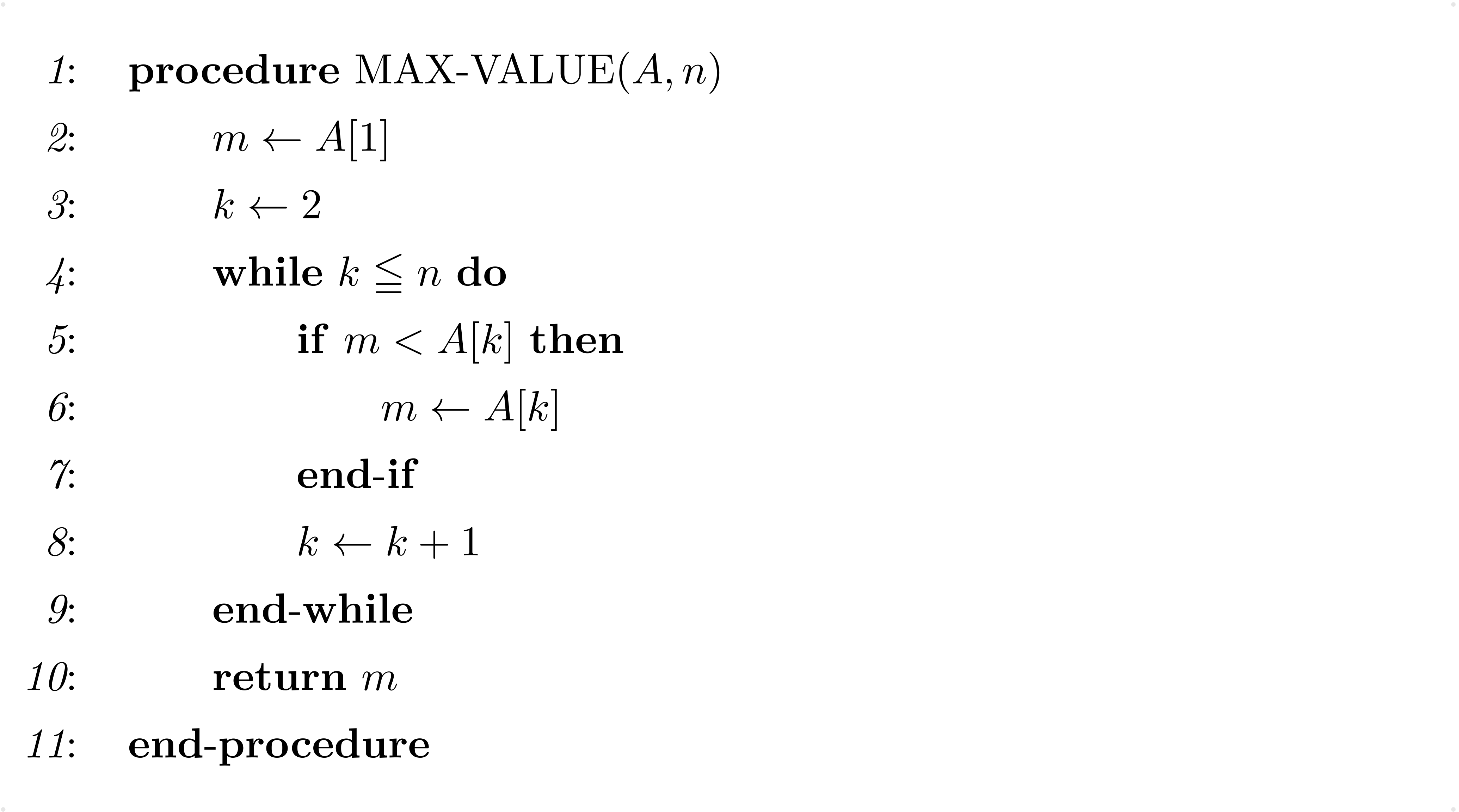
僕「A[k] という表記は $a_k$ を表しているんだよね」
テトラ「はい、そうです。配列というのは、 同じ種類のデータが、 コンピュータのメモリ上に一列に並んでいるようなデータ構造です。 プログラミング言語によっては最初の要素が0番になっていることもよくありますが、 先日の講座では最初の要素が1番になっていました。 こちらの配列のイメージ図は、 $$ \LLRR{31,41,59} $$ という三つの数からなる数列を配列で表現した様子です」
配列のイメージ図

僕はList 4を読んで、どんな処理をやっているかを理解した。理解したと思う。
けれど、さっきと同じように早合点をやらかしてはまずいので、もう一度じっくりと読み返した。
僕「……」
テトラ「……」
僕「うん、これについては特に問題はない……と思うけど。 テトラちゃんは何か気になることはあったの?」
テトラ「はい。一つ気付いたことがありました。 List 4では $n \GEQ 1$ が前提になっている、と思ったのです」
僕「nは要素の数だよね」
テトラ「はい。もしも、 $n = 0$ だとしたら、 List 4の2行目で、A[1]というありえない要素の値を得ることになってしまいますから」
僕「なるほど! 確かにそうなるなあ。 ああ、それは一つ前のList 3でも同じ前提があったわけだね」
テトラ「そうですね。 ですから、アルゴリズムについて語るときには、 こんなふうに入力と出力を明記することが大事なんだと再確認したんです」
List 5
MAX-VALUE: 最大値をもとめるアルゴリズム(配列版)
入力
出力
手続き
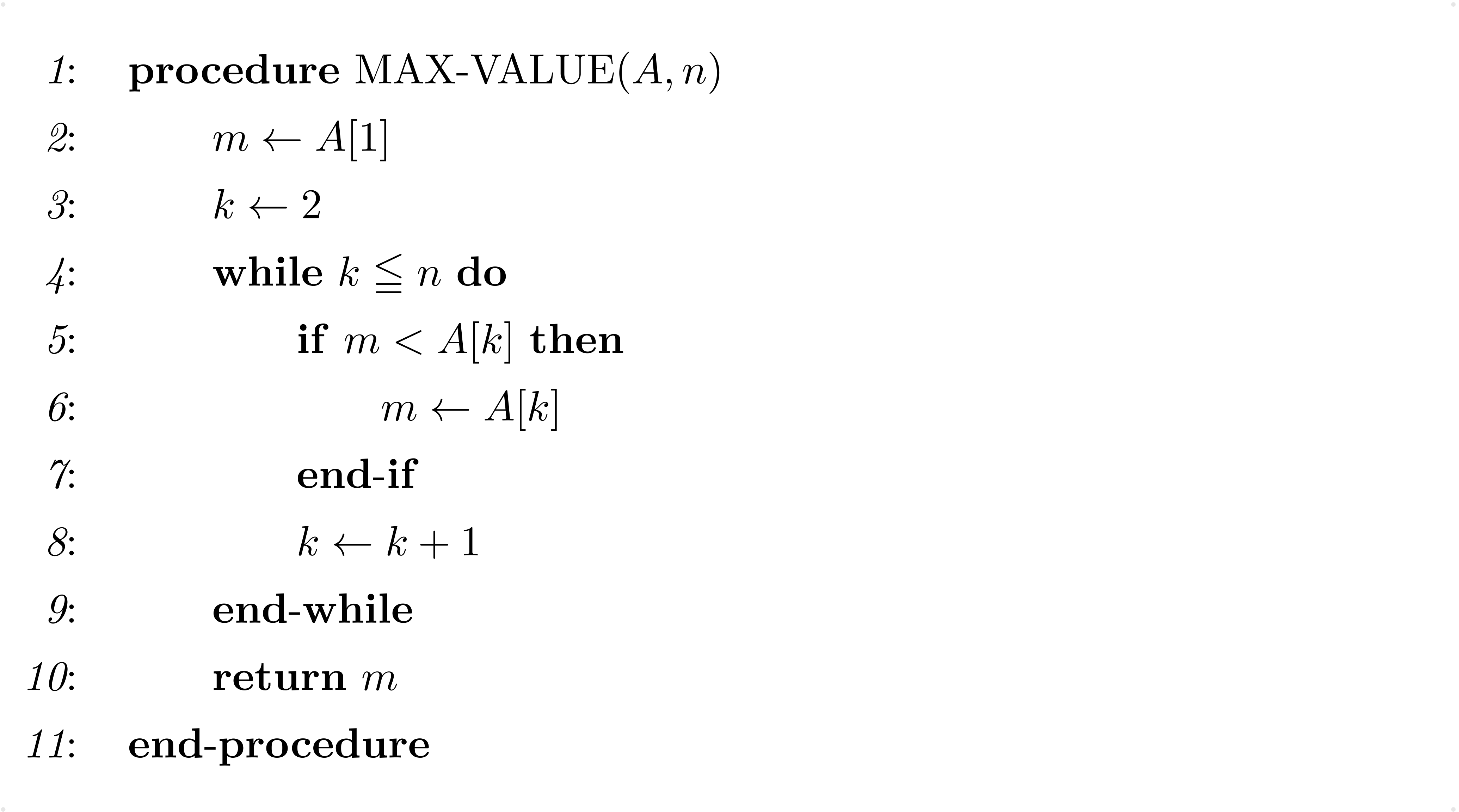
僕「うーん……」
再度、僕は反省した。
簡単だとあなどる気持ちがあると、 アルゴリズムを読むのは難しいんだな。
テトラちゃんは一つ一つをていねいにしっかりと考えて読んでいる。 《条件忘れのテトラちゃん》なんて、もう言えないな。
テトラ「次からが難しくなってきます。 次は線形リストを使って最大値を求めるアルゴリズムを表現したものです」
List 6
MAX-VALUE: 最大値をもとめるアルゴリズム(線形リスト版)
入力
出力
手続き

僕「あちこちに出てくる c.next というのは何を表しているの?」
テトラ「はい、それは次のノードを指すリンクを表しています」
僕「リンク?」
テトラ「たとえば、 $\LLRR{31,41,59}$ という数列を線形リストで表したものは、こんな図で表現します」

僕「なるほど?」
テトラ「間に仕切りが入った長い四角はコンピュータのメモリ上にある《ノード》という領域を表しています。ここには三個のノードがあります。 ノードがメモリ上のあちこちにあって、データを保持している……と考えます。三個のノードがそれぞれに $31,41,59$ という三個の数を保持しているんです」
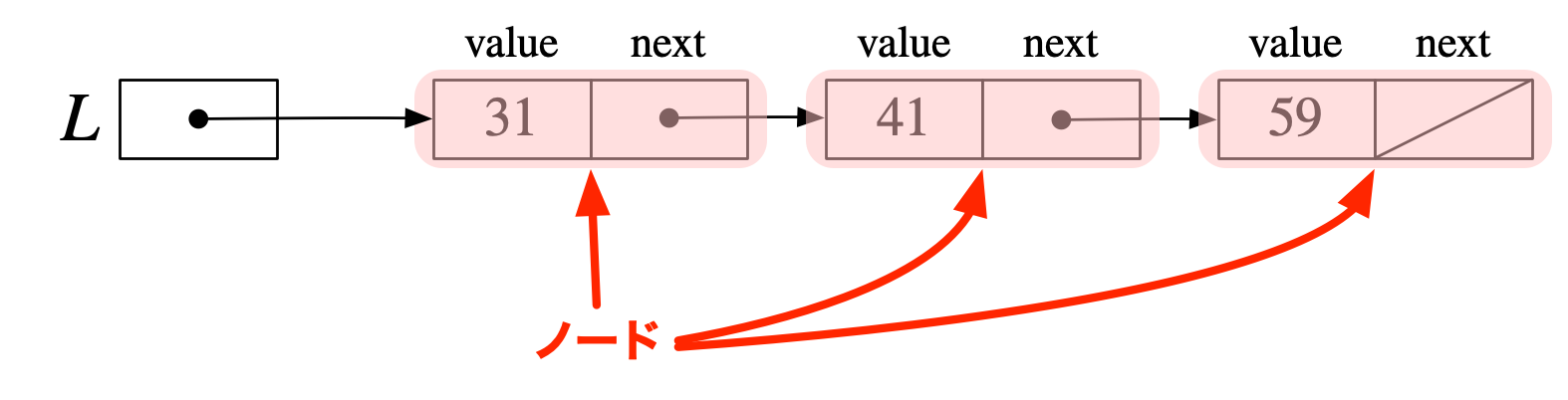
僕「うん」
テトラ「一つのノードはいくつかの《フィールド》に区切られています。 今回の場合はvalueとnextという二つのフィールドがあります」
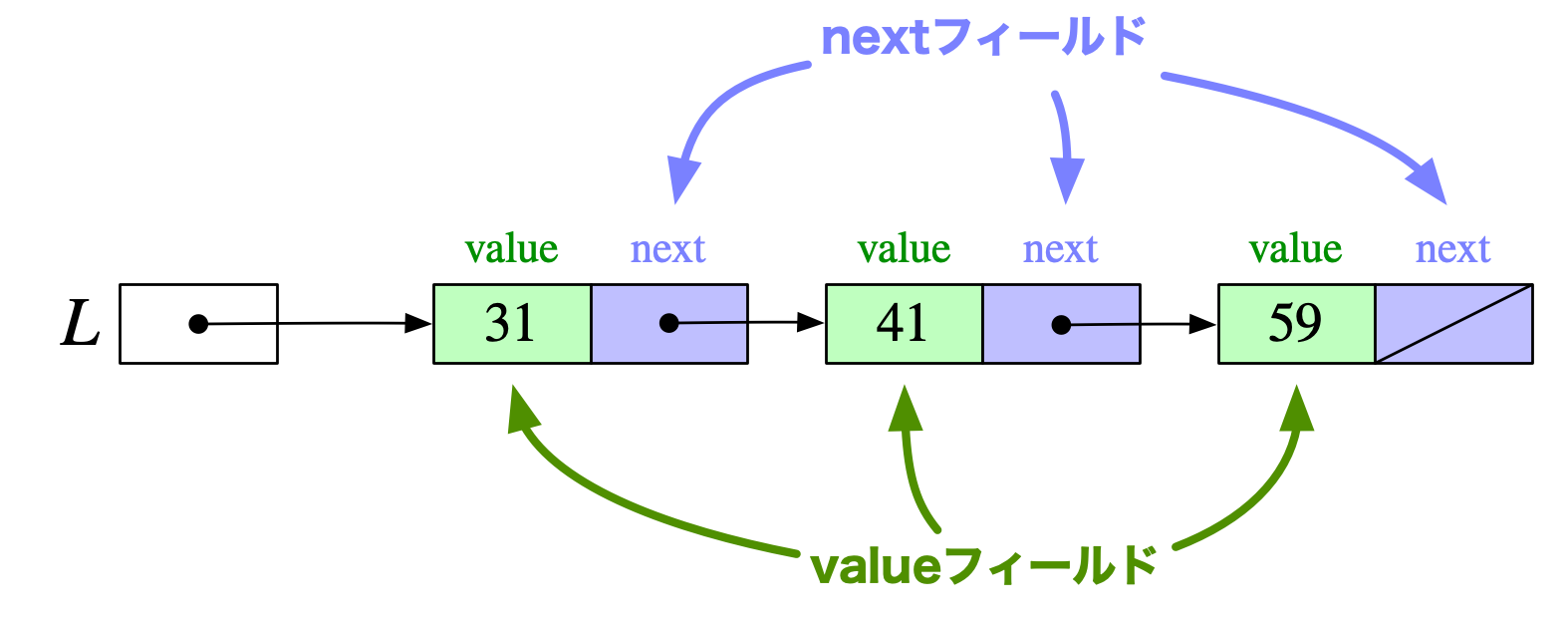
僕「valueフィールドの値はわかるけど、nextフィールドのリンクというのは抽象的だね」
テトラ「はい。そうですね。実際にはコンピュータ上では、メモリのアドレスが保持されていると考えればいいと思います。 《ノードはここにある》と指しているのでポインタと呼ばれることもあります。 リンク、アドレス、ポインタはだいたい同じ概念です。 コンピュータの中でつじつまが合っているなら、リンクの具体的な値は何でも構いません。たとえば、こうかもしれません」

僕「nextフィールドの値が、次のノードのアドレスになっているイメージなんだね。 nextの値が次のノードを《指している》ということだ」
テトラ「はい、そうです! なので、図では矢印を使って表現しています。リンクを使って、鎖のように次々とノードをつなぐことで、複数の要素からなる数列が表現できるんですっ!」
僕「この最後のノードのnextフィールドにある斜線は、終わりの印だよね。nilって書いてある」
テトラ「はいはい。斜線は、nextフィールドの値が《どこも指していない》という場合に使う表現です。 線形リストの場合にはリストの終わりを表しています。 プログラミング言語ではNULLやnullやNoneなどと表現されますが、講座ではnil(ニル)という表現を使っていました。 あたしはnowhereという名前がいいなと思ったんですが」
僕「……」
僕はList 6のアルゴリズムを改めて読み返していた。
テトラちゃんの説明でおおよそは読めるようになったけれど、 これは、やはり……
テトラ「このアルゴリズムを理解するために、 あたしは $\LLRR{31,41,59}$ という小さな具体例で実際にウォークスルーしてみることにしました。 《例示は理解の試金石》ですから!」
僕「そうだよね!」
僕とテトラちゃんはいっしょにList 6の動きを、一歩一歩順番に確かめていった。

(1)→(2)→(3)で、mの値が決まったところ
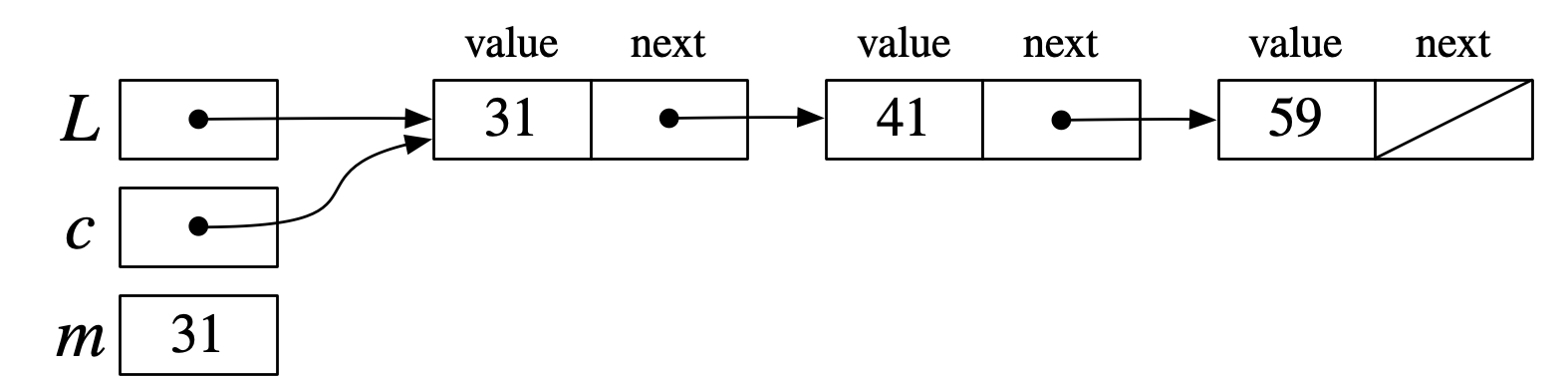
(4)→(5)→(6)で、mとc.valueを比較するところ
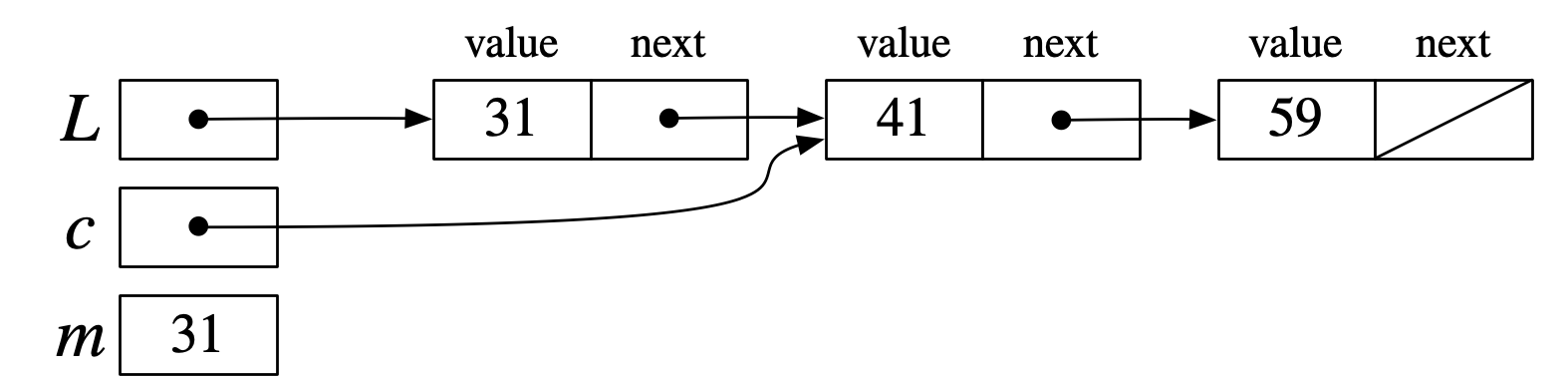
(7)→(8)→(9)→(10)→(11)→(12)で、再度mとc.valueを比較するところ
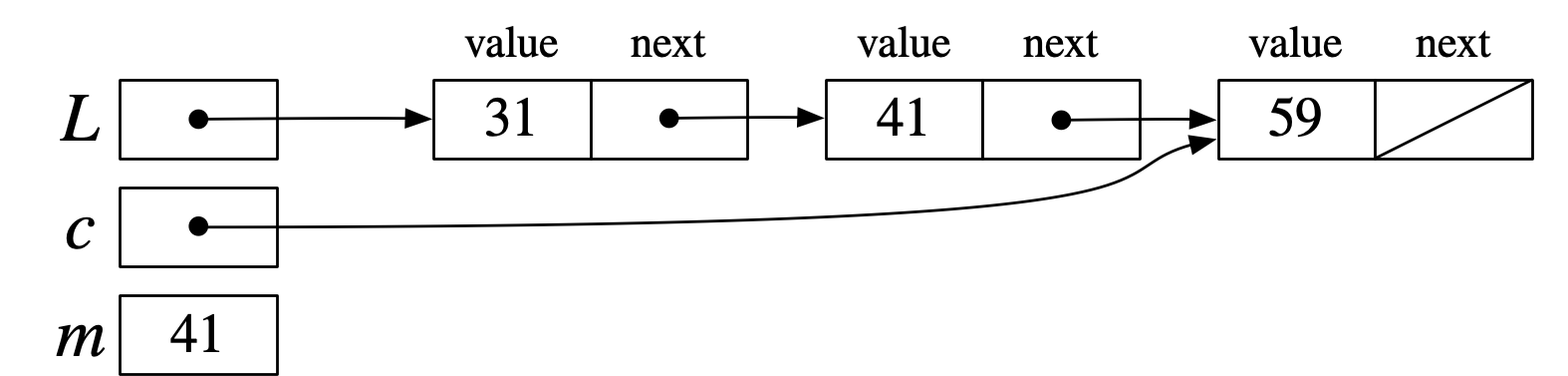
(13)→(14)→(15)→(16)→(17)→(18)で、(19)の終了直前
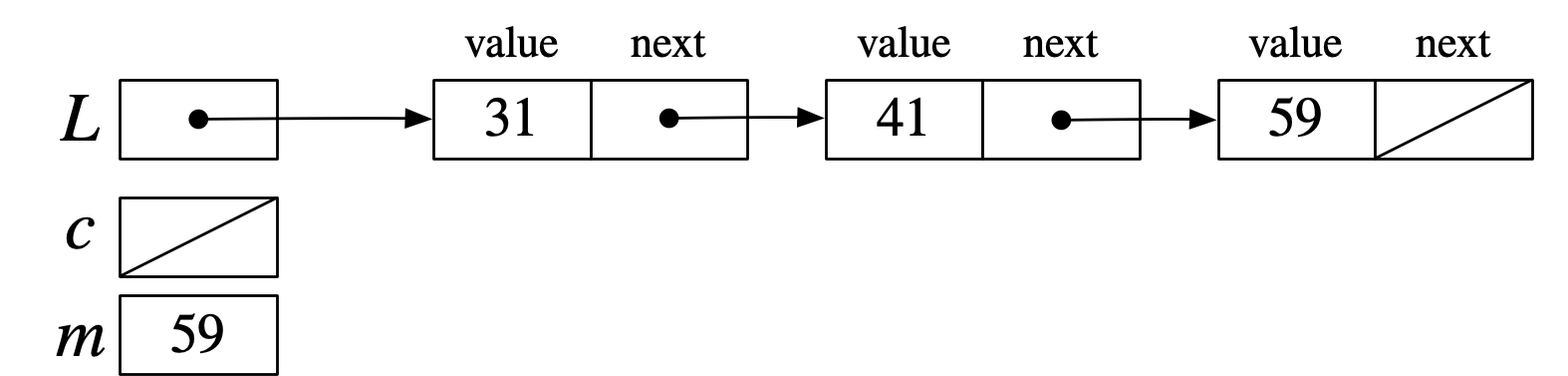
テトラ「確かに、最大値の $59$ が得られています!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第321回終わり)
(2021年4月30日)