![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好き。
ここは高校の図書室。いまは放課後。
そろそろ帰ろうかなと思ったところに、後輩の元気少女テトラちゃんがやってきた。
テトラ「あっ、先輩! ちょうどいいところに。村木先生から《カード》がやってきましたよ!」
村木先生というのは、僕たちにときどき数学の問題を出す数学教師だ。
数学の問題を出すというか、思わせぶりな《カード》を渡してくることが多いかな。
そこには数学の問題が書かれていることもあるし、単に数式が書かれていることもある。何も書かれていないことすらあった。
僕たちはその《カード》をきっかけにして自由に考え、ときに問題を自分で作って、解く。そんなふうにして数学を楽しんでいるんだ。
……さてさて今日は?
僕「新作の《カード》は問題が書かれてた?」
テトラ「え、ええとですね。問題とはいえませんね」
僕「だったら意味ありげな数式かな?」
テトラ「というわけでもないです」
僕「何も書かれていないパターン? 何だか今日のテトラちゃんは意味ありげだね」
テトラ「そういうわけでもないんですが、まるで……トランプのようなカードなんです」
僕「トランプって?」
テトラ「たとえば、これが1枚目にいただいた《カード》です。コバルト1ですね」
僕「コバルトワン」
《カード》コバルト1
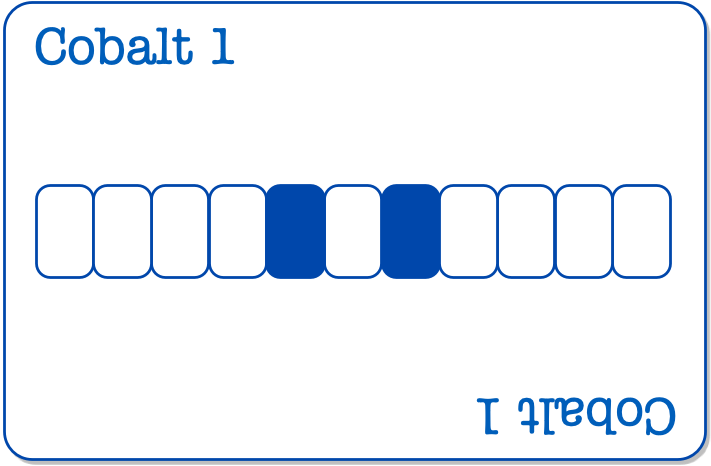
テトラちゃんが机の上に置いた《カード》は確かにトランプに似ていた。
ハートのエースや、スペードの3じゃなくて……コバルト1?
テトラ「コバルトというのは、たぶん cobalt blue という色を意味してるんだと思います」
僕「なるほど、コバルトブルーね……まあ、色はいいとして、この絵柄は何を表しているんだろう。白と青の並び」
テトラ「左右対称になってます」
僕「裏は……裏には何も描かれてない。ちょっと待ってテトラちゃん。『1枚目』って言ってたけど、コバルトツーもあるの?」
テトラ「はい、そうです。これがコバルト2ですね」
《カード》コバルト2
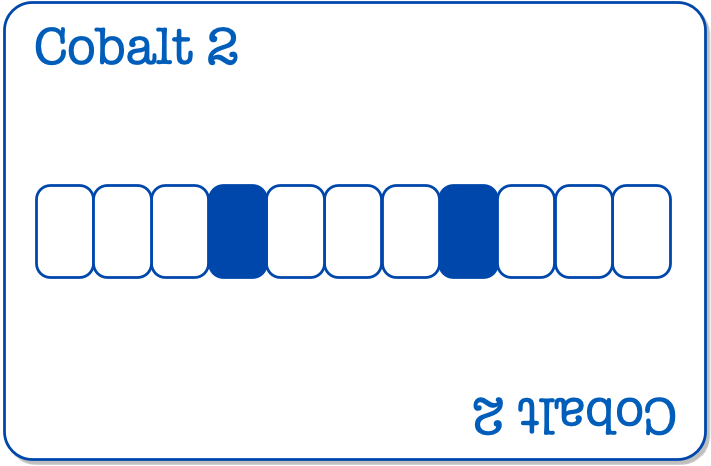
僕「ちょっと青の位置が違うね。広がってる。この2枚から何かを考えるのは無茶だと思うんだけど、もしかして、コバルトスリーもあるの?」
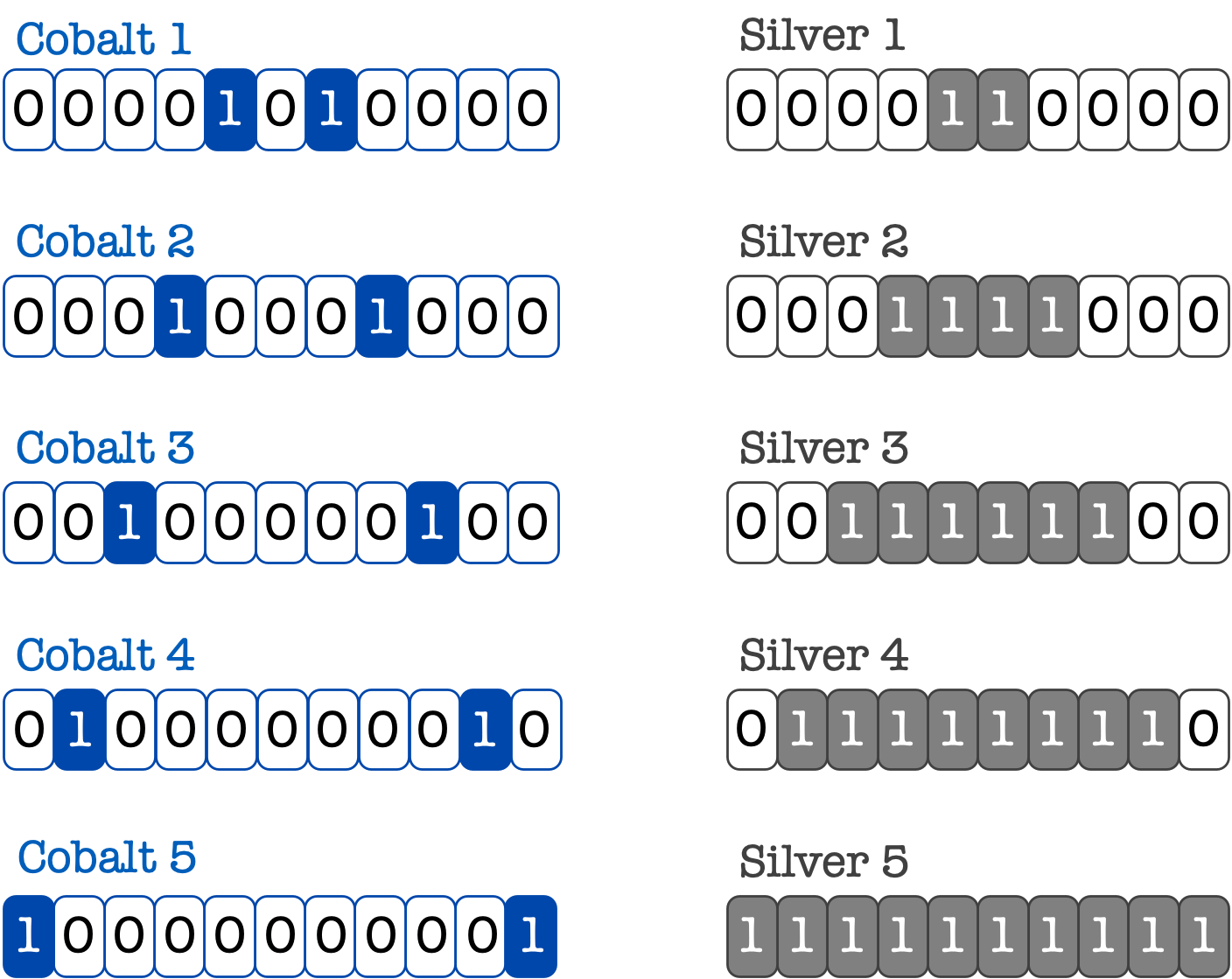
テトラ「はい、実はコバルト1からコバルト5までいただいてきました。 もっと作れるけれど図案的に難しいのでコバルト5までにしたんだそうです」
コバルト1からコバルト5

僕「もっと作れるけど図案的に難しい……村木先生って、思わせぶりなところに無駄に力を注ぐときあるよね。まあ、ともかくこの図案は規則的。数が大きくなると広がっていく。全部で11個の並ぶ場所があって、そのうち2個が青で残りの9個が白と」
テトラ「はい。コバルトの方はそうなってますね」
僕「コバルト以外もあるの?」
テトラ「はい。シルバーもあります。これがシルバー1ですね」
《カード》シルバー1
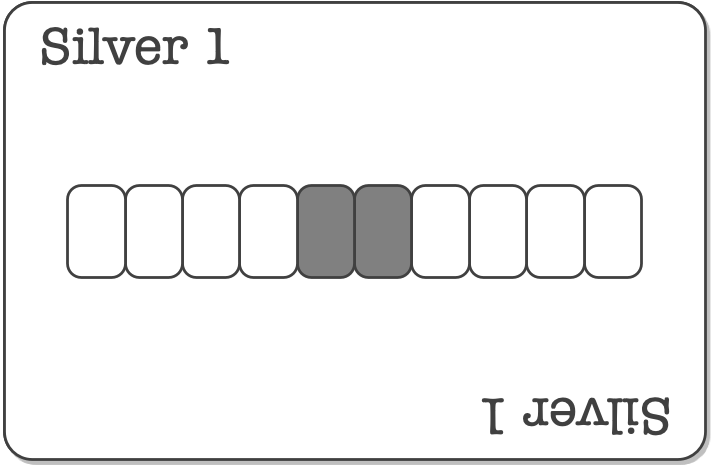
僕「シルバーだから銀色ってことか。実際は灰色だけど」
テトラ「こちらもシルバー1からシルバー5まであります」
シルバー1からシルバー5

僕「これで全部? ダイヤモンド4とかタンザナイト5とか出てこない?」
テトラ「これで全部です。結局あたしがいただいたのは全部で10枚の《カード》になります。コバルトが5枚、シルバーも5枚。 《コバルトとシルバー》だそうです」
《コバルトとシルバー》

僕はしばらくこの10枚の《カード》を見ながら、考える。
何かおもしろいことはないか、と考える。
10枚の《カード》は、いかにも意味ありげで、それっぽい規則性もある。
でも……
僕「でも、これだけだと何とでも解釈できちゃうよね」
テトラ「ですよね……でも、あたしがいただいたのはこの10枚だけなんです」
僕たちが考えあぐんでいるところに、赤いノートブック・コンピュータを抱えたリサがやってきた。
いつもなら、無言のまま一人で離れた場所に座る彼女だけれど、今日は僕たちが話しているところにまっすぐやってきた。
登場人物紹介(追加)
リサ:自在にプログラミングを行う無口な高校生。赤い髪の《コンピュータ少女》。
リサ「村木先生から《プリント》」
リサはテトラちゃんに紙を1枚渡す。
テトラ「あ、あたしですか? すみません……でもこれが《プリント》?」
《プリント》

僕「おっ、数式っぽいものがやってきたぞ! 村木先生はこれもテトラちゃんに渡そうとしてたんだね」
テトラ「そうかもしれません……これは計算でしょうか」
僕「そうだね。右辺を計算すれば左辺になるってことかな」
テトラ「あっ、リサちゃん! 待ってください。リサちゃんはこれ、何だと思いますか?」
リサ「『ちゃん』は不要。ビットパターン?(咳)」
リサはその一言を残していつもの席に向かい、コンピュータを開いた。
テトラ「ビットパターン……」
僕「ああ、なるほど。確かにビットパターンかも。 《カード》の絵柄を《0と1の並び》に見立てる。 たとえば《白は0》で《青や銀は1》とか?」
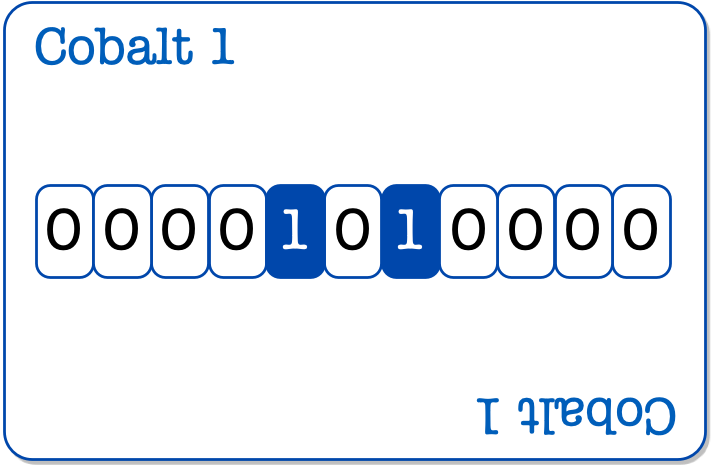
テトラ「コバルト1だったら00001010000ということでしょうか」
コバルト1は00001010000になる?
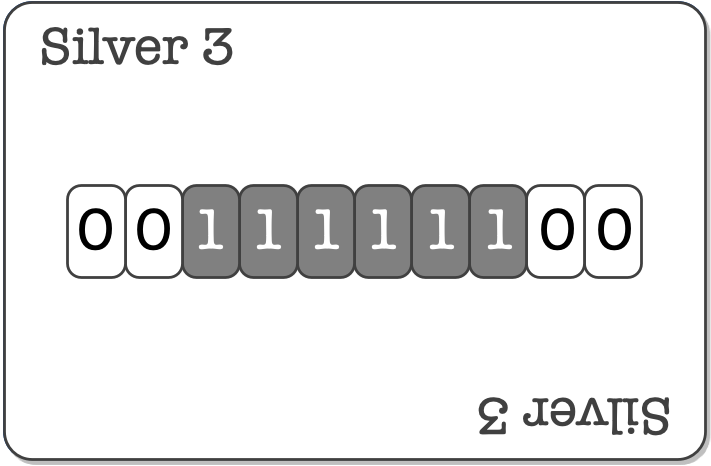
僕「それはありえそうだよね。シルバー3なら0011111100になる。そして、すべての《カード》は二進法で表された数と考える」
シルバー3は0011111100かな?
テトラ「はいはい……ええと、二進法とすると、こうですね」
《コバルトとシルバー》を二進法で表された数と見なす
僕「たとえばコバルト1を二進法の00001010000だとして、それを十進法で表せば80ということになるね。1が立っているところが $2^6, 2^4$ の二カ所だけだから」
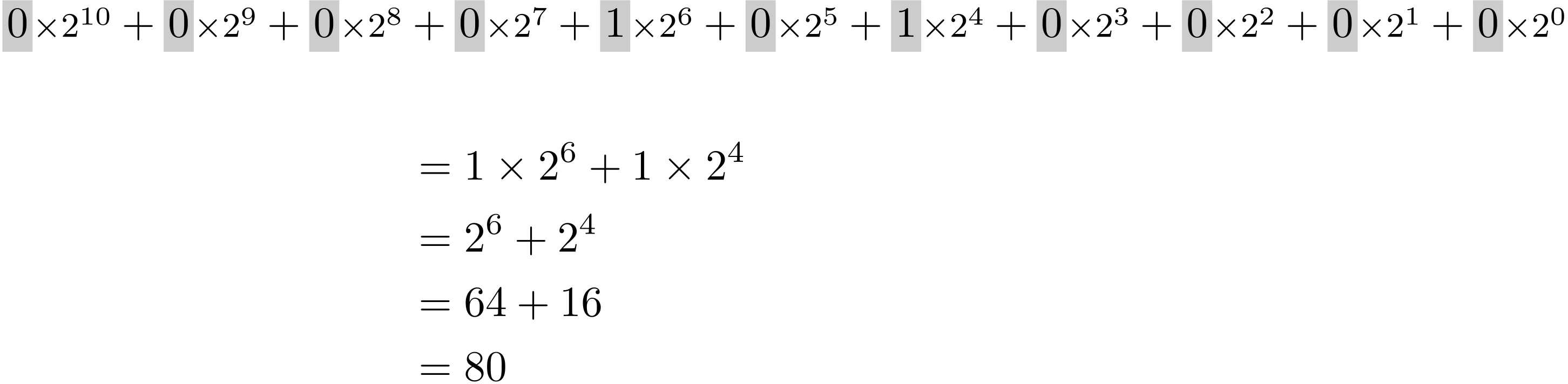
テトラ「ああ、だったら話は簡単ですね。《カード》は数を表していて、リサちゃんの持ってきてくれた《プリント》はその計算式を表している……のかも?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2021年3月12日)