![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/図形の証明』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ノナ:ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
母「はい、お茶どうぞ」
ユーリ「ありがとうございまーす」
ノナ「ありがとうございます $\NONA$」
ここは僕の家。
ノナとユーリといっしょにずっと数学トークを続けてきたので、 ちょっとくたびれた。
タイミングよく母さんからの《おやつコール》が来て、 みんなでおやつのケーキを食べているところ。
ケーキはノナが持ってきてくれたもので、 生地の上に栗の味がする甘いクリームが毛糸のたばのように盛られていて、 その上には甘く煮た大きな栗が乗っている。栗づくしでとにかく甘い。僕にはちょっと甘すぎて……
ユーリ「お兄ちゃん、お兄ちゃん。モンブランってゆー名前があるんだからね。 そんなにややこしい解説しなくても、《モンブラン》って一言いえばちゃんと伝わるの!」
僕「地の文にツッコミ入れるなよ」
ノナ「おいしい $\NONAHEART$」
母「いつもお持たせでごめんなさいね。お母さんによろしくお伝えしてね、ノナちゃん」
ノナ「はい $\NONA$」
ノナはそう答え、母が台所に戻っていくのをずっと目で追っていく。
僕「ノナちゃんは、三角形の合同条件にだいぶ慣れてきたよね。それから数学の証明についても」
ノナ「はい $\NONA$」
ユーリ「三角形の合同の話、二等辺三角形の底角の話、あと何やったっけ」
僕「そのくらいだよ。『二等辺三角形の底角は等しい』と、その逆の『二つの角が等しい三角形は二等辺三角形』の証明をいっしょに書いたよね」
ノナ「おいしい $\NONAHEART$」
僕「別の三角形の話をしようか。たとえば正三角形はどうだろう」
ユーリ「いーよー」
ノナ「大丈夫 $\NONA$」
僕「ノナちゃんは、正三角形の定義は知ってる?」
ノナ「辺がぜんぶ等しい $\NONAQ$」
僕「うん、そうだね。もう少し言葉を補う方がいいよ。たとえば『正三角形とは、三辺の長さがすべて等しい三角形のことです』のようにね。 ちょっと言ってみて」
ノナ「正三角形とは……三辺の長さがすべて等しい三角形のことです $\NONA$」
僕「それでいいよ。どんな言葉を補ったか、わかる?」
ノナ「正三角形とは $\NONAQ$」
僕「そうだね。それも大事だけど、一番大事なのは『三角形』だよ。 ノナちゃんは『辺がぜんぶ等しい』とだけ言ったけど、それを聞いた人の心には、ある《疑問》がふわふわと浮かんでくる」
ユーリ「ノナは、辺の長さがすべて等しいとゆーけれど、それは《何》の話をしてるのかにゃ?」
僕「そういうこと。『辺がすべて等しい』だけだと、三角形なのかどうかわからない。 辺の長さがすべて等しい四角形なのか、辺の長さがすべて等しい五角形なのか……何を言ってるかわかる?」
ノナは、モンブランを食べ終えて、こくんとうなずいた。
僕「正三角形は確かに辺の長さがすべて等しいよ。それは正しい。 でもその前に、正三角形はそもそも《三角形》だよね。 三角形にはいろんな種類がある……無数にあるけれど、その三角形の中で特に、《三辺の長さがすべて等しい》という性質を持ったものに名前をつけましょう。 それは《正三角形》という名前です」
僕はできるだけやさしい声で、ゆっくりと話す。
ノナはきちんと僕の話を聞いている。大丈夫、伝わっている。
ノナ「はい $\NONA$」
僕「ノナちゃんが誰かに『どういうものを正三角形というんですか?』と質問されたとする。 それに対して答えるとしたら何といえばいいか。それが正三角形の定義だね。 答えるとしたら『正三角形というのは、三辺の長さがすべて等しい三角形のことです』といえば、きちんとした答えになる。 もちろん、答え方はいろいろあるけれど」
ノナ「あの $\NONA$」
僕「はい?」
ノナ「あの……うまく《外》に出なかったみたい $\NONA$」
僕「なるほど、ノナちゃんの心の《中》ではちゃんと正三角形を思い描いていたんだね。 三角形で、しかも、三辺の長さがすべて等しいものを」
ノナ「三角形はあたりまえだと思った……思いました $\NONA$」
ユーリ「正三角形は三角形!」
僕「うん、確かにあたりまえだ。僕たちがふつうにおしゃべりしているときは、それで通じる。 でも、あらためて『正三角形の定義は?』と問いかけたときは、あたりまえのこともちゃんと言わないとね。 数学で定義はとても大事だから」
ノナ「理由 $\NONAQ$」
僕「?」
ノナ「定義は……定義は理由になるから大事です $\NONA$」
僕「そう! その通り。証明をするときに、定義を使って説明したり、 定義を使って式を立てたりするから大事なんだね。 ノナちゃんはよくわかっているよ!」
ノナ「$\NONAHEART$」
ユーリ「正三角形は三角形だし、正三角形は二等辺三角形だよね」
ノナ「$\NONAQ$」
僕「うん、ユーリがいいことを言ったね。『正三角形は二等辺三角形である』というのは、どういう意味かわかる?」
ノナ「正三角形は、二等辺三角形 $\NONA$」
ユーリ「どんな正三角形でも、二等辺三角形といえるってことでしょ?」
僕「そういうことだね。ノナちゃんはいまのユーリの説明を聞いて『確かにそうだ』って納得できる?」
ノナ「なんとなく……はい $\NONA$」
僕「ユーリは、そんなノナちゃんにはっきりと理由を説明できる?」
ユーリ「できるよん。正三角形は三つの辺の長さが等しいじゃん? ってことは、二つの辺の長さは等しいわけ。だからそれは二等辺三角形でもある」
ノナ「わかった……わかりました $\NONA$」
僕「そうだね。定義を確認してみると、こうなる」
ノナ「はい $\NONA$」
僕「正三角形と呼ばれる三角形が何かあったとする。 そうすると、正三角形の定義から、その三角形は三辺の長さが等しい。 三辺の長さが等しいということは、そのうちの二辺の長さは等しい。あたりまえだけどね」
ノナ「はい $\NONA$」
僕「ということは、二等辺三角形の定義から、その三角形は二等辺三角形といえる」
ノナ「はい $\NONA$」
ユーリ「ダウト!」
僕「おいおい、何がダウト?」
ユーリ「ダウトってゆーか、二等辺三角形の定義があやしー! 『二辺の長さが等しい』じゃなくて『少なくとも二辺の長さが等しい』じゃね?」
僕「ああ、まあ、確かにね。確かに『少なくとも』とつけた方がより親切だね。 でも『二辺の長さが等しい三角形を、二等辺三角形という』でもまちがいじゃないよ。 だって残りの一辺については何もいってないんだから。等しいとも等しくないともいってないからね」
ユーリ「あー、そっか」
ノナ「二等辺三角形も三角形……三角形ですか $\NONAQ$」
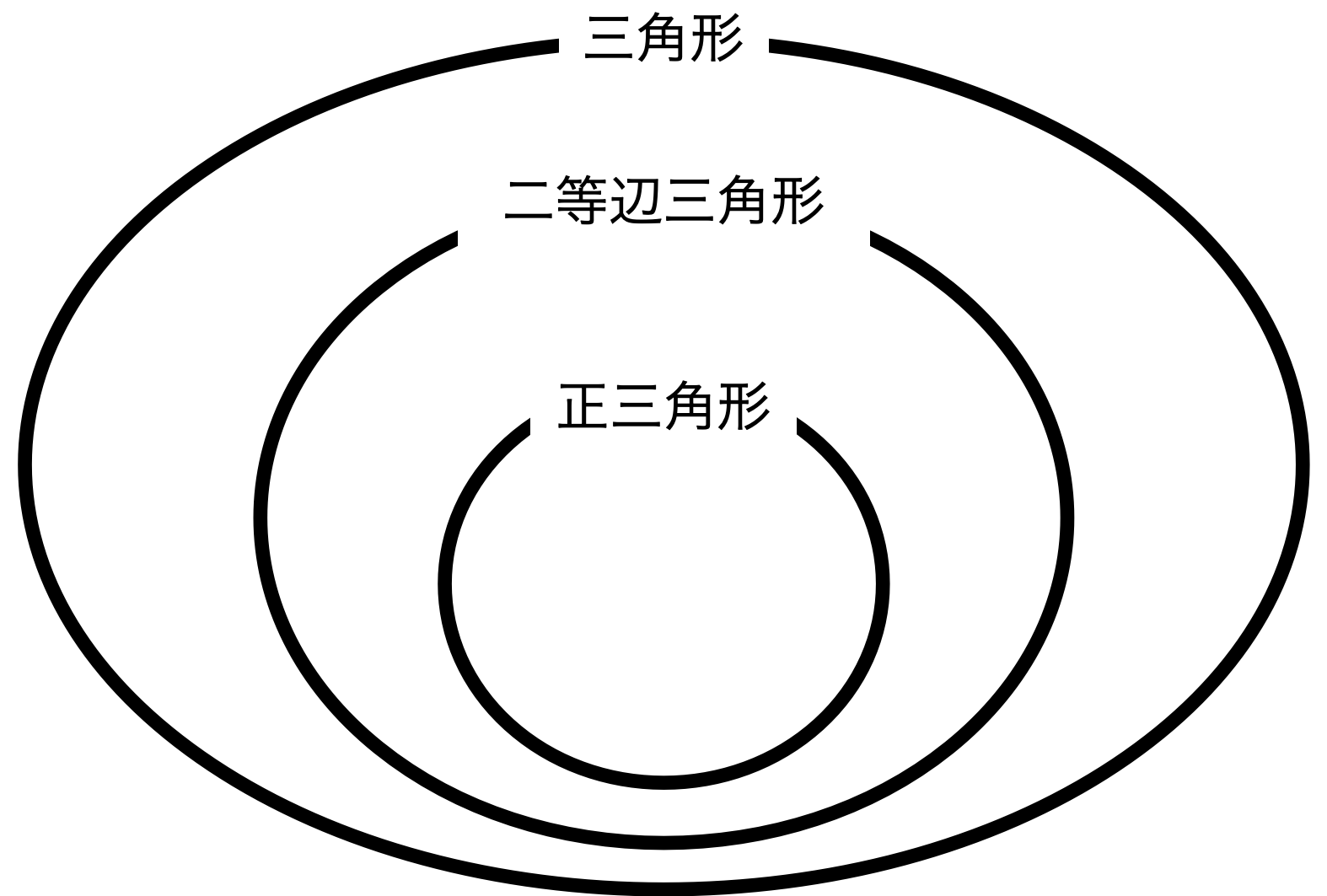
僕「うん、そうだよ。二等辺三角形も三角形だよ、もちろん。だから、正三角形と、二等辺三角形と、三角形の関係はこんな図で表現できる」
正三角形・二等辺三角形・三角形
ユーリ「そだね」
ノナ「$\NONA$」
僕「ノナちゃんは、この図が何を表しているかわかる?」
ノナ「ダメ……全然ダメです $\NONAX$」
ユーリ「えー、わかるじゃん!」
僕「ユーリ、ちょっと待って。ノナちゃんは、この図を見て『全然ダメ』なのかな? ノナちゃんの《中》には、わかっていることがあるんじゃない? 『こういうことかなあ』という考えがあるなら、ゆっくりでいいから《外》に出してみようか、ね?」
ノナは前髪をちょっと引っ張ってから、小さな声で話し始める。
ノナ「正三角形は……二等辺三角形です $\NONA$」
僕「うん」
ノナ「二等辺三角形は……三角形です $\NONA$」
僕「そうだね」
ノナ「それ……それがこの図です $\NONAQ$」
僕「そういうことでいいんだよ。ノナちゃんは偉いね。 いま、自分の《中》にある考えを、自分でちゃんと言葉にして《外》に出すことができたから」
ノナ「できました $\NONAHEART$」
僕「この図は、正三角形と二等辺三角形と三角形がどういう関係にあるか……それを表すつもりで描いたんだ。 ぜんぜん説明しないで『わかる?』と聞いちゃったけどね。 ちょうど、学校のグラウンドに大きなマルを三つ、こんなふうに描いたようすを想像すればいいね。 正三角形と書いたマルの中には正三角形を置くことにする。そうすると、正三角形は二等辺三角形のマルの中にも入っていることになる」
正三角形は……

……二等辺三角形でもある。

ノナ「はい $\NONA$」
僕「つまり、マルがどういう重なり方になっているかを使って、 正三角形と二等辺三角形と三角形の関係を表しているんだ」
僕は、こういう関係のことを包含関係(ほうがんかんけい)と呼ぶこともあるよ、と言いかけて、いったんストップ。
そんなことよりも、この図で遊んだ方がよさそうだ。
僕「この図で、正三角形は一番内側にあるマルの中に入る。それから正三角形じゃない二等辺三角形は正三角形のマルの外で二等辺三角形のマルの中に入る。 だったら、《ココ》に入る三角形はどんな三角形だと思う?」

ノナ「二等辺三角形じゃない三角形……です $\NONA$」
ユーリ「せいかーい!」
僕「そうだね。ノナちゃん、それでいいよ。ココに入る三角形は、二等辺三角形のマルの外側にあるけど、三角形のマルの内側にある。 だから、二等辺三角形じゃない三角形になる」
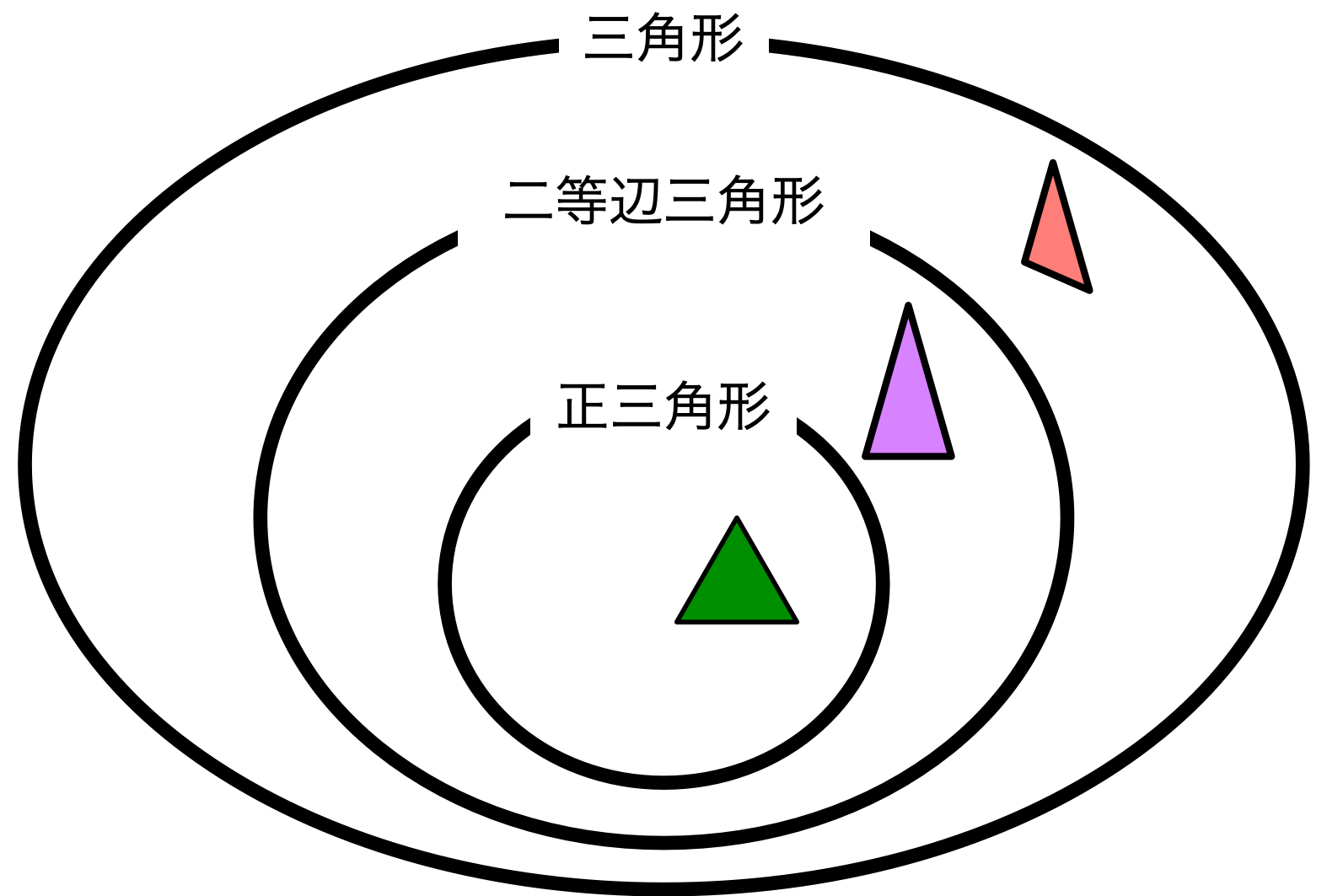
ユーリ「つまり、三辺がぜんぶ違う長さの三角形!」
僕「そうそう、そういうことになる」
ノナは、深く納得したように何度もうなずいた。
そうなんだよな。ノナはきちんと時間を掛けて、ひとつひとつ確かめていけば理解できる。
反応が悪いように見えても、それは単に別のことに気を取られているだけのことも多い。
そしてノナが『全然ダメ』と言ったとしても、それは単に……言葉として自分の《外》に出すのを恐がっていたり、 ミスしてしまうのを嫌がっていたり、正解以外の表現をしてしまうことをためらっていたり……することが多いのだ。
自分の《中》にある概念を取り扱うことと、その概念を言葉にして《外》に取り出すことは違う。
《外》に出てくる言葉を支えるものは何だろう。もちろん用語を記憶しておくことや、 数学的概念を知っていることや頭の中で操作しておくことも大切だ。 でも、それよりも深いところで、すべてを支えているものがある。
それは、何と言えばいいんだろう。《大丈夫》といえばいいのか、《安心》といえばいいのか、《自信》といえばいいのか……
まちがっても《大丈夫》だから、思い切って言葉にする。
怒られたり、馬鹿にされたりしないから、《安心》して表現する。
ひどくおかしな考え方をしているわけじゃないという《自信》から、思いついたことをそのまま出してみる。
それらが、《外》に出てくる言葉を支えているし、言葉を《外》に出すことを支えているんじゃないだろうか。
そして、それは、数学に限った話ではなくて……
ユーリ「……ゃん! おにーちゃん! おーい、もどってこーい!」
ユーリの声に、僕は我にかえる。
ユーリ「ねーねー! 正三角形の問題ってないの? ノナが証明してみたいって!」
ノナ「そんなこと言ってないよう $\NONAEX$」
ユーリ「いーじゃん、いーじゃん。お兄ちゃんは、きっとハイパーウルトラ超絶楽しい問題出してくれるって!」
僕「ハードル上げるなよ……うん、これがちょうどいいよ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年11月6日)
この記事は『数学ガールの秘密ノート/図形の証明』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!