![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/図形の証明』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ノナ:ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
僕「三角形の合同条件は三つあるんだよ。二つの三角形があったとして……」
僕「……この三つだね。たった三つだから覚えるのはそれほど難しくない。でも、三つの合同条件が何を意味するか、よく理解しないと使えない。だから、まず三辺相等から詳しく話すよ」
ユーリ「ストップ!ストップ!お兄ちゃん!お兄ちゃん!早すぎ!早すぎ!」
僕「あっと!……ごめんごめん、また早すぎちゃったよね、ノナちゃん?」
ノナは、緊張した顔でこくん、とうなずいた。
ノナ「ゆっくり……ゆっくりお願いします $\NONA$」
今日は土曜日。ここは僕の家のリビング。
僕と、いとこのユーリと、そしてノナがいっしょにテーブルで勉強をしている。
勉強というかなんというか……ノナが数学を学ぶのを手伝っているところ。
ユーリもノナも中学生だから、そんなに難しい数学じゃない。いちおう僕は高校生だしね。
ユーリ「まったく! お兄ちゃん、ホントに何回言っても早口になるよね。これでもう、ワンアウトだよ」
僕「スリーアウトになると何が起きるんだろう」
ユーリ「チェンジじゃん」
いとこのユーリはいつもおしゃべりしている仲良し。 だから、間合いもよくわかっている。 ユーリがどんなことに興味を持ち、 どんなふうに考えそうかはだいたいわかる。
でも、ノナは違う。
ノナ「$\NONA$」
ノナはユーリの同級生。
ひょんなことから僕は彼女に数学を教えることになった。
これまで僕たちは何回か数学トークを重ねてきたけれど、 それでもいまだにわからない。ノナがどんなふうに何を考えているのか、僕には、よくわからないのだ。
それに、僕の側の問題もある。自分が知っている話だと、早口になってしまうこと。 これは以前から言われてきたのに、いまだに直らない。努力はしているんだけどな。
僕「うん、じゃあ、ゆっくり行くよ。今日は三角形の合同条件の話」
僕はそう言って、ひと呼吸置く。そして、ノナの反応を待つ。
ノナ「はい $\NONA$」
ノナはユーリと同い年だけど、ずいぶん小柄な体格だ。
丸い眼鏡を掛けていて、やや垂れ目。かわいらしいけれど、ふわふわした話し方とあいまって、だいぶ幼い印象がある。
ノナは、いつもベレー帽をかぶっている。 それは彼女のトレードマークのようだ。 トレードマークというか、アイデンティティなのかな。 そして……ちょっぴりのぞいた前髪の一部が銀色になっている。 《ひとふさだけの銀髪メッシュ》なのだ。
僕「……どうかな? 話を先に進めても大丈夫?」
ユーリ「だいじょぶだよ。三角形の合同条件っしょ?」
ノナ「さんかっけいの……ごうどうじょうけん $\NONAQ$」
僕「そうだね。三角形の合同条件の話をしようとしている。三角形はわかるよね?」
ノナ「知ってる……知ってます $\NONA$」
ノナは人差し指でテーブルの上に三角形をゆっくり描く。
僕「そうそう。それが三角形。三つのまっすぐな辺で囲まれた図形だね。三つの角があるから三角形」
ノナ「合同条件はわからない……わかりません $\NONA$」
僕「うん、これから話をするから、いまはわからなくても大丈夫。 合同条件というのは、二つの三角形はどういうときに合同といえるのか……それを表す条件のことだよ。 ノナちゃんは三角形の合同はわかる?」
ユーリ「ごうどう」
ノナ「ごうどうは、知ってる……知ってます $\NONA$」
僕「じゃあね、『二つの三角形が合同である』ということを説明してみて」
ノナ「わからない……わかりません $\NONA$」
ノナはそういって、銀髪を指でひっぱる。
ユーリ「ノナ、こないだわかってたじゃん!」
ノナ「わかんなくなったんだもん $\NONA$」
僕「うん、大丈夫だよ。ノナちゃんは、うまく説明できないと思ってるんじゃない? 完全に正しい答えを言えなくてもいいんだよ。 まちがってもいいし、何となくでもいいよ。『二つの三角形が合同である』とはどういうことだと思う? 教えてほしいな、ノナちゃん」
ノナ「おんなじ……三角形が同じ $\NONAQ$」
僕「うん、そうだね。合同というのは、ある意味では、二つの三角形が同じということ。 でも、三角形が同じというだけじゃ不正確。 ノナちゃんは、だいたいのことはわかっているみたいだから、少しずつ正確にしていこう。 具体例があった方が話しやすいかな」
僕は、グラフ用紙に三角形を描く。
僕「たとえば、ノナちゃんは、この二つの三角形を合同だと思う?」
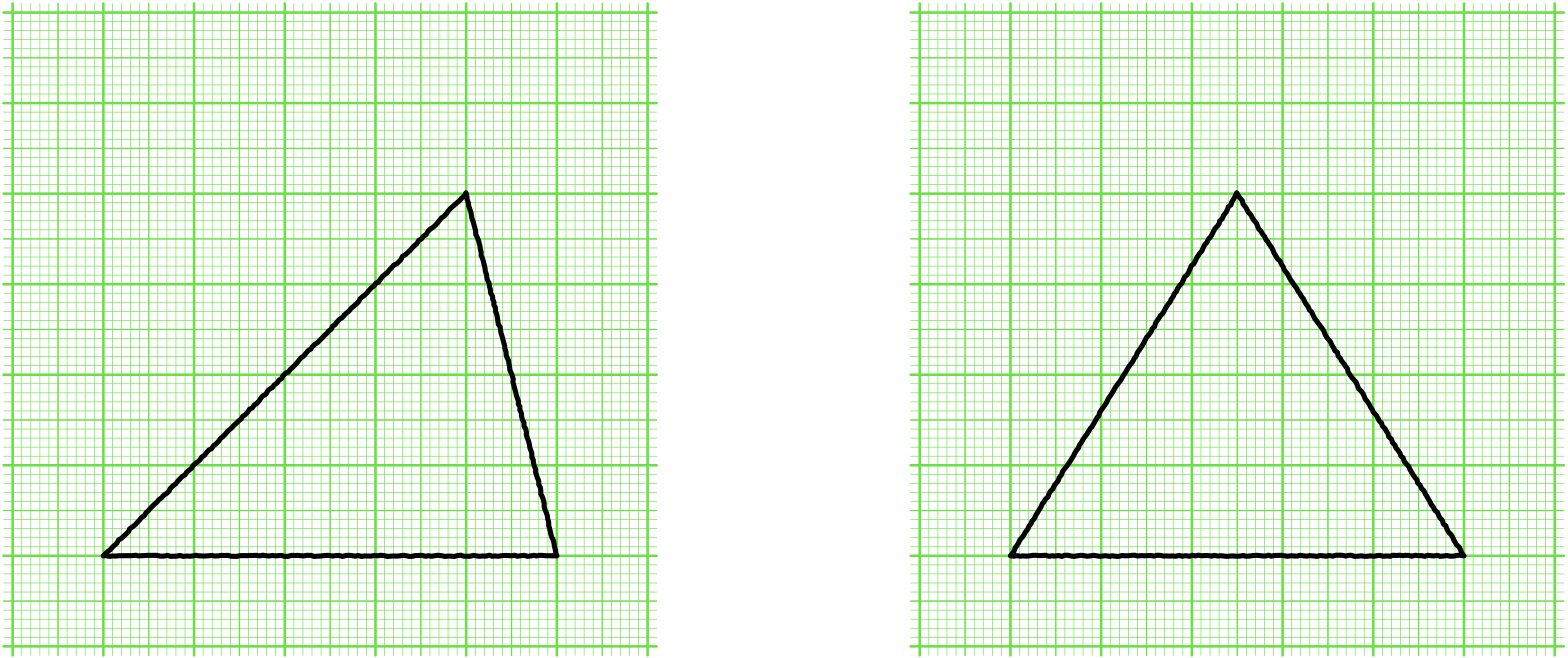
ノナ「ちがう……ちがいます $\NONA$」
僕「そうだね。ノナちゃんのいう通りだよ。 この二つの三角形は合同じゃない」
ノナは、数回うんうんうん、とうなずいた。
僕「この二つの三角形は合同じゃない、でも面積は等しいんだ。 この三角形二つは、面積が等しいという意味では《おんなじ》だけど、でも、合同とはいえない」
この二つの三角形は、合同じゃない。

僕「じゃあ、ノナちゃんは、この二つの三角形は合同だと思う?」
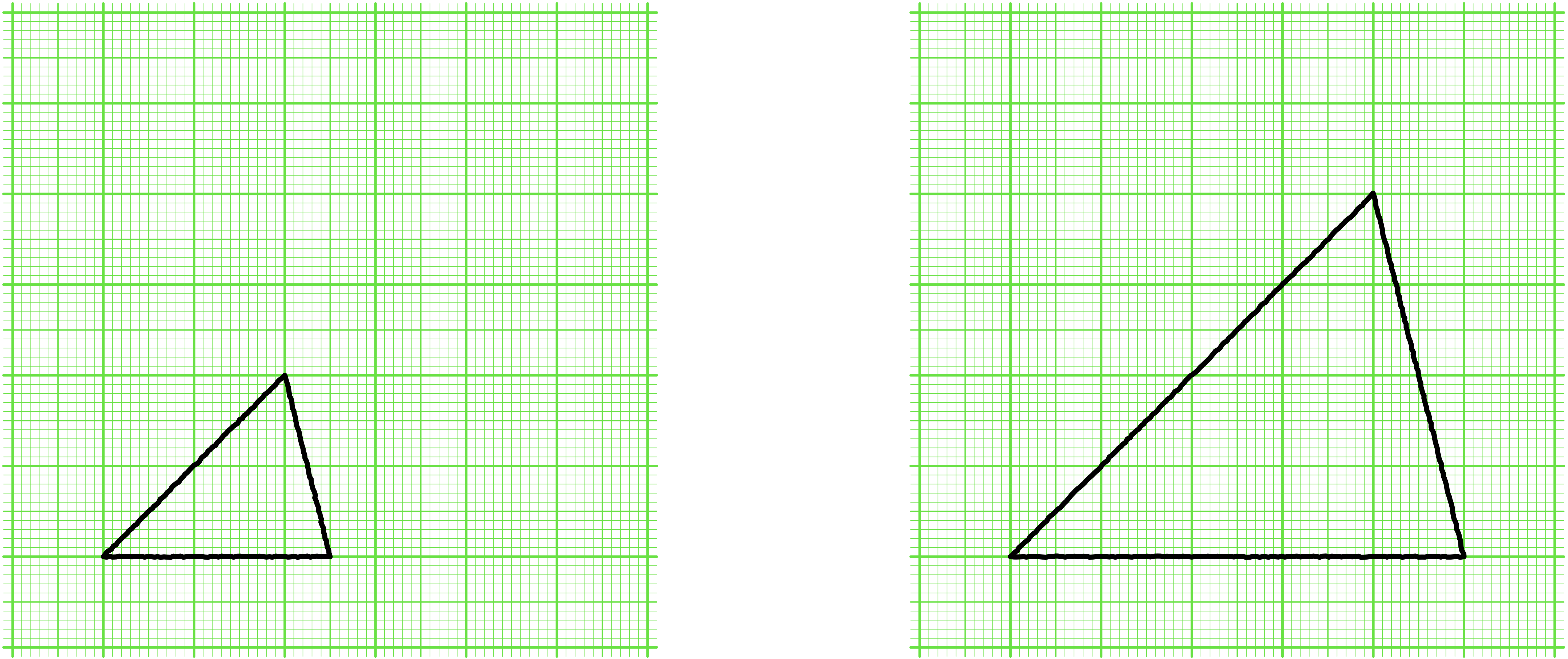
ノナ「ちがう……ちがいます $\NONA$」
僕「ノナちゃんの言う通り。この三角形は合同じゃない。合同じゃないけど、二つの三角形の三組の角の大きさは、それぞれ等しい」
ユーリ「左の三角形をぐーっと大きくすると右のになるみたい」
僕「そうだね」
ユーリの言葉に反応して僕は『二つの三角形があって、三組の角の大きさがそれぞれ等しいとき、その二つの三角形は相似(そうじ)になってる』 と言いたくなったけれど、ぐっとこらえる。いまは合同の方に集中しよう。
僕「……三組の角の大きさがそれぞれ等しいという意味では、この二つの三角形は《おんなじ》だけど、合同じゃない」
ノナはもう一度こくん、とうなずく。
この二つの三角形は、合同じゃない。
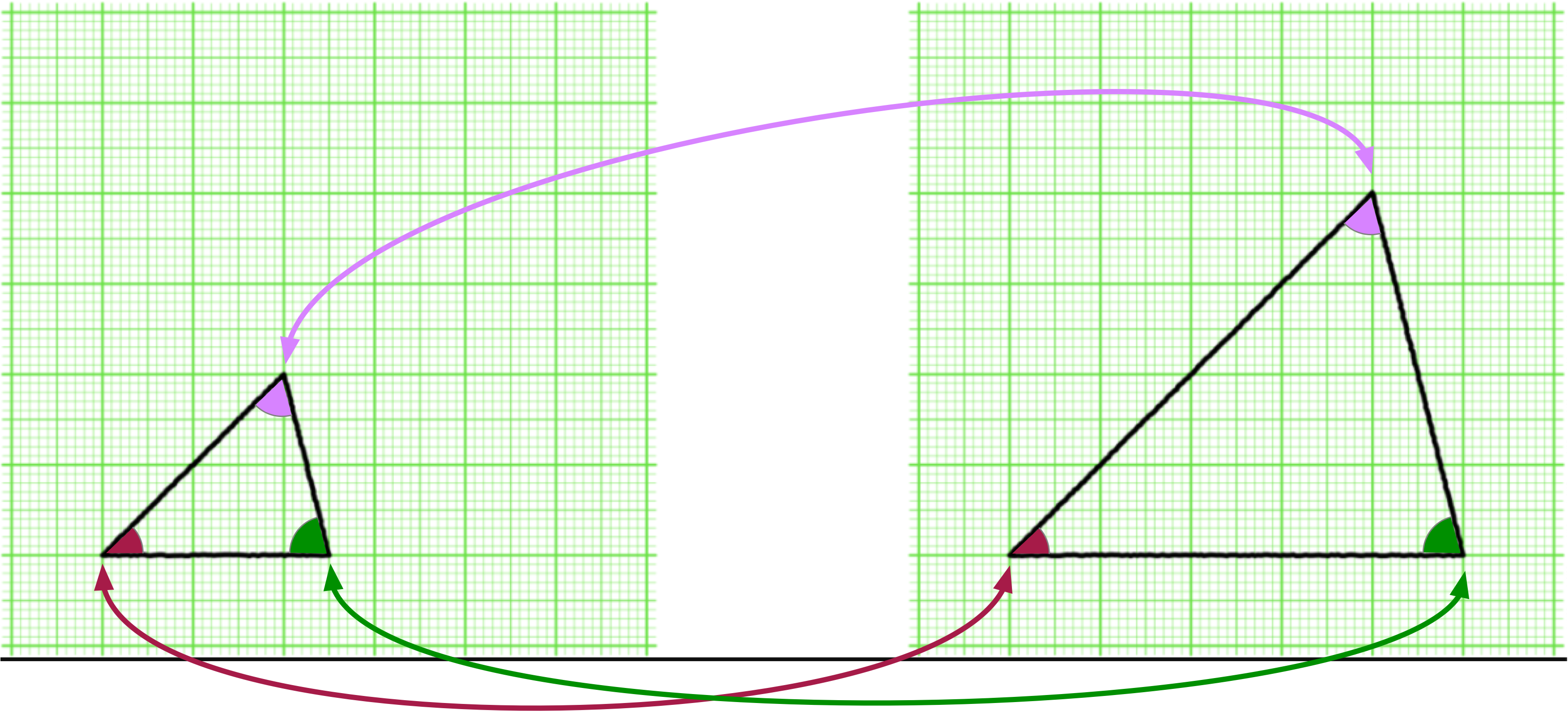
僕「具体例(1)や(2)でわかるように、二つの三角形が《おんなじ》というだけだと、意味がはっきりしない。 面積のことを言ってるのか、三つの角の大きさのことを言ってるのか、それとも別のことを言ってるのかわからないから。そうだよね?」
ノナ「『同じ』だと、合同じゃないかも……合同にならないかも $\NONAQ$」
僕「うん、そうだね。 単に《おんなじ》というだけだと、合同を意味したことになるかもしれないし、ならないかもしれない。 それだとちゃんと話を進めることは難しい」
ノナはもう一度こくん、とうなずく。その拍子に丸眼鏡が少しずれ、彼女は両手で位置を直す。
僕「でもノナちゃんは、具体例(1)や、具体例(2)で、二つの三角形が合同じゃないとわかった。 ということは、ノナちゃんは『二つの三角形が合同である』というのが、 どういうことなのか、きっと知っているんだよね、うまく説明はできなくても」
ノナ「習った……習いました $\NONA$」
僕「なるほど。 三角形の合同は学校で習ったんだ」
ノナ「ぴったり重なるの……重なります $\NONA$」
ノナは、両手の人差し指を重ね、重ねたまま指を動かしてテーブルに三角形を一つ描く。
彼女の中では二つの三角形が重なっているのだろう。
僕「そうだね! そんなふうに、二つの三角形をぴったりと重ねることができるとき、 その『二つの三角形は合同である』と呼ぶことにするんだ」
ユーリ「えー、でもお兄ちゃん。《ぴったりと重ねることができる》って、 それって数学になんの? もっと、こー、厳密な話じゃないの?」
僕「確かに《ぴったりと重ねる》というのは、ずいぶん僕たちの感覚を頼りにしている言い方だと思うよ。 でも僕たちは《ぴったりと重ねる》というのが何を意味しているかよくわかっている。 厳密に合同とは何かを追求するのもいいけれど、まずは先に進もう」
ユーリ「ふむふむ、よかろー。話を進めたまえ」
僕「ユーリ、えらそうだな」
ノナ「ユーちゃん、えらそう $\NONA$」
僕たちはいっしょにくすくす笑った。
『先に進もう』と僕が言ったのは正直な気持ちだった。
ノナの理解を助けるために、ゆっくり進むのは大事だけれど、どうしても先に進みたくなる。
もちろん、ノナを置いてけぼりにしてまで先に進むのは意味がないのだけれど。
僕「ノナちゃんは、この二つの三角形は合同だと思う?」
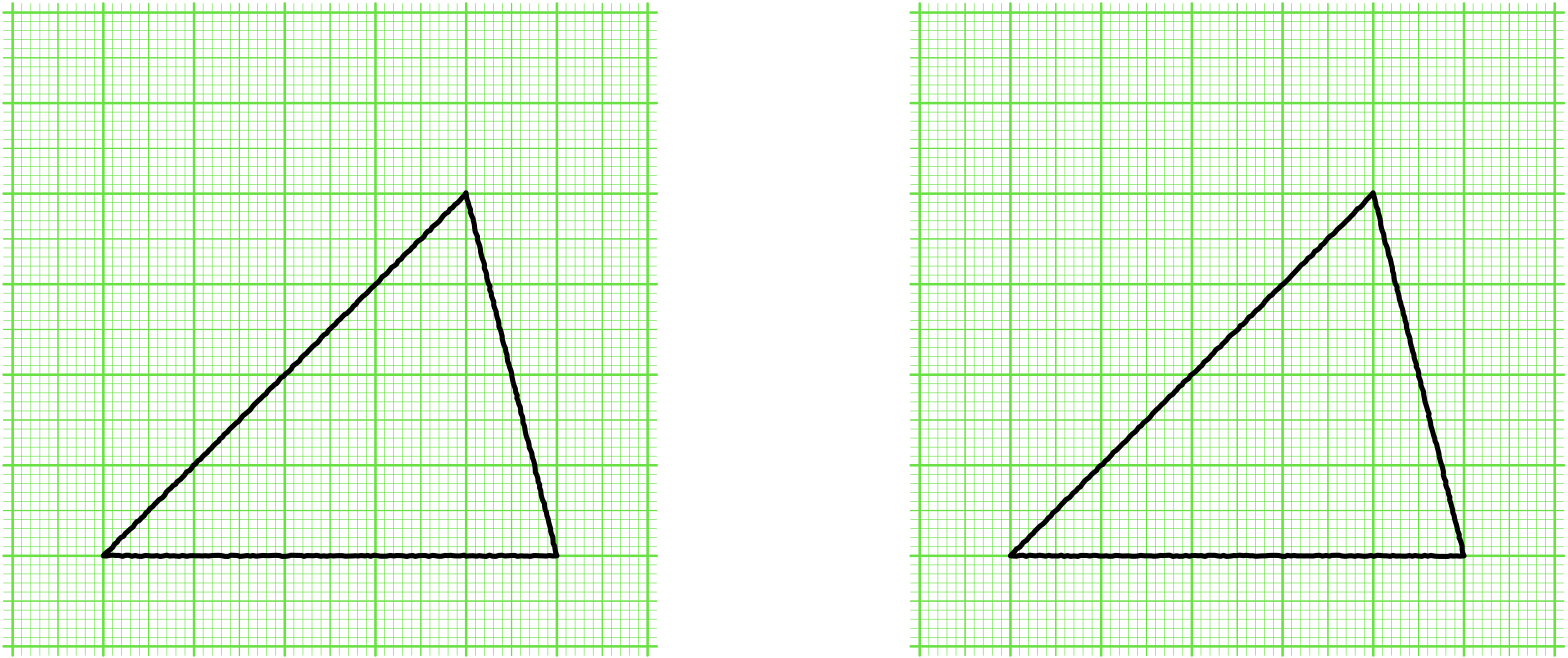
ノナ「合同です $\NONAEX$」
僕「そうだね。正解だよ!」
ノナは、強くうなずいた。
僕「この二つの三角形は、合同だよ。そしてこの二つの三角形は、面積も等しい。三組の角の大きさも、それぞれ等しい。それから、三組の辺の長さもそれぞれ等しいね」
この二つの三角形は、合同である。

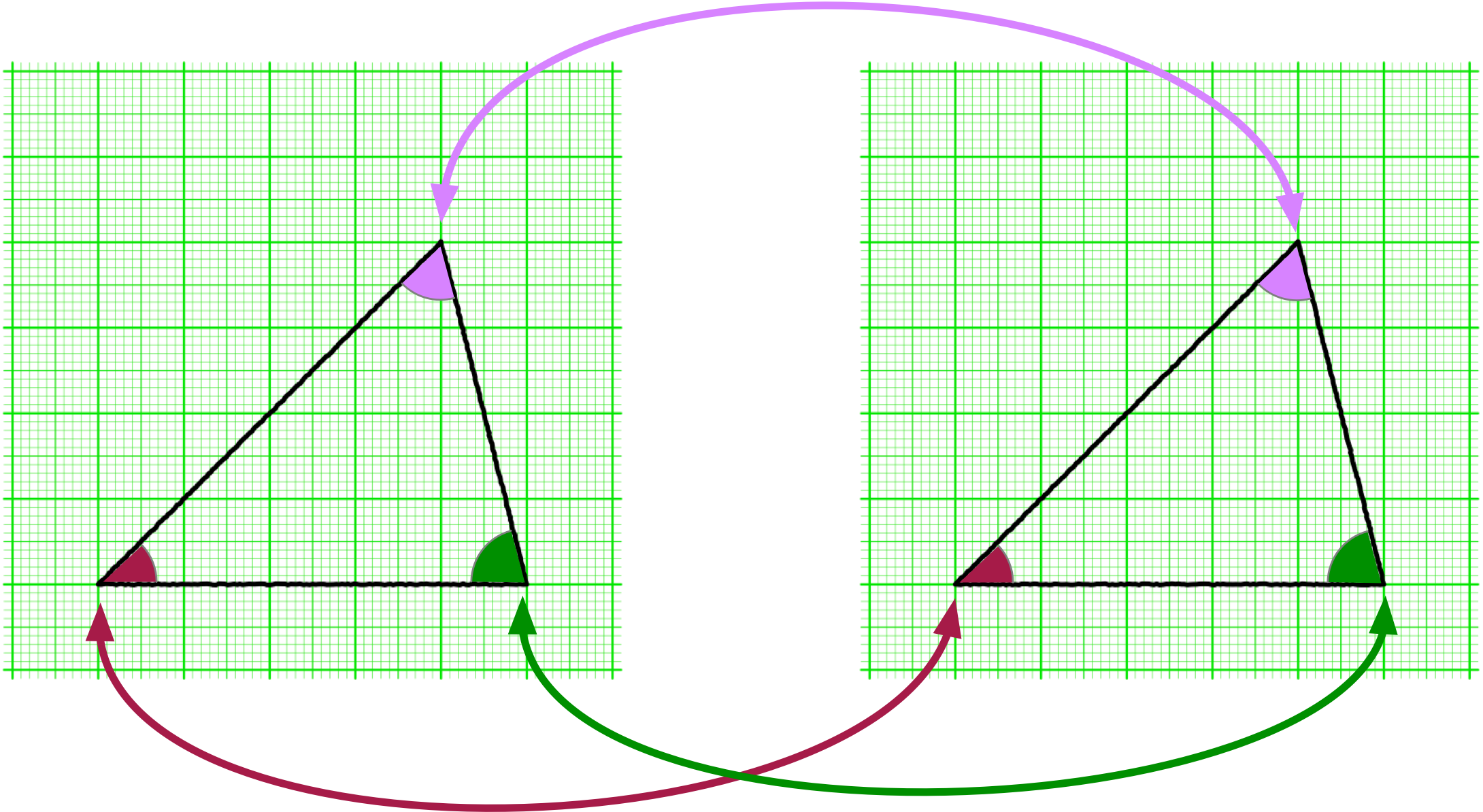
ノナ「合同……合同です $\NONA$」
僕「そうだね。ところでこの二つの三角形はどうして合同だと言えるの? そう言える理由は何だろうか」
ノナは、瞬時に顔を曇らせる。そして、きょろきょろ目を動かす。
ノナ「同じだから……違う。『同じ』じゃない $\NONA$」
ユーリ「ぴったりと重ねることができるから、でしょ?」
ユーリは、がまんできないように言う。
僕「そうだね。ノナちゃんが言うように、この二つの三角形は合同だよ。それはまちがいじゃない。 そして、どうしてこの二つの三角形が合同だといえるのか。 その理由は、ユーリがいうように、この二つの三角形を《ぴったりと重ねる》ことができるから」
ノナ「難しい……難しいです $\NONA$」
ノナは、心底困ったように低い声を出す。
僕「わかったような、わからないような感じがするかもしれないから、順を追って整理するね」
僕は、ノナのようすを見ながらゆっくりと話す。
ノナは僕の話を真剣になって聞いている。彼女のようすを注意深く見ていると、理解しているかどうか、わかるときがある。
自信がないときや、気になることがあるときには、彼女は急激に落ち着かない動きをするからだ。
いまは大丈夫。ノナは僕の話についてきている。
僕「さっき僕は『どうしてこの二つの三角形が合同といえるか』と尋ねたよね。 そのときは、この(イ)を尋ねていたんだ」
ノナ「$\NONA$」
僕「僕たちの目の前には具体的な三角形がある。そして『この三角形は合同だ!』 と言うためには、理由が必要になる。『ナントカだから、合同だ』や『合同といえるのは、ナントカだから』という言い方になる……大丈夫?」
ノナ「聞いてる……聞いています $\NONA$」
僕「そこでカギになるのは、定義だよ。僕たちは『二つの三角形が合同である』ということを、 『二つの三角形をぴったりと重ねることができる』ことだと定義したよね」
ノナは軽くうなずく。
僕「この二つの三角形はぴったりと重ねることができる。だから、合同だといえることになる」
ノナ「理由は定義……定義ですか $\NONAQ$」
僕「理由を聞かれたなら、いつも定義を答えればいいかという意味かな? いや、そうとは限らないよ。 定義を答えればいいときもあるし、もっと別のことを答えることもある。 でも、定義を答えたり、定義にしたがって答えたりする場合はとても多いね」
僕がそういうと、丸眼鏡の奥でノナの目が迷うように動いた。
きっと、彼女の中で何かが動いたんだ。言葉を補ってみよう。
僕「理由を聞かれるというのは、説明のどこかに大きな省略があるときなんだよ。 『あれあれ? 話が飛んでるよ! それじゃわからない。説明の途中が抜けてるぞ』ってこと、ない?」
ノナ「いっつも……いつもです $\NONAEX$」
僕「数学では説明をするときに、理由を聞かれることがよくあるよ。 それは説明の途中で話が飛んだときや、話が飛んでないことを確かめたいとき」
ユーリ「お兄ちゃん、よく理由を聞くよね」
僕「そうだね。『ここに描かれた二つの三角形が合同といえるのはどうして?』と僕が聞いたのは、 ノナちゃんは合同の定義をちゃんとわかっているかな、と思ったからだよ。 理解を確かめたかったんだ」
ノナ「..kw.と..k.りms $\NONA$」
僕「え? 何? ごめん、よく聞こえなかった」
ノナ「恐いとき……あります $\NONA$」
僕「何が恐いの?」
ノナ「『どうして』$\NONA$」
僕「『どうして?』や『なぜ?』と聞かれるのが恐いときがあるってことかな」
ノナ「ときどき $\NONA$」
僕は、以前のノナとの対話を思い出した。ああ、そうだよね。
僕「うん……キツい言い方で『どうして?』と聞いてくる人はときどきいる。それから『なぜ?』を、責めるみたいに言う人もいる」
ノナ「はい $\NONA$」
僕「でも、数学では違うよ。 数学で『どうして?』というのは理由を尋ねる言葉なんだ。 だから、ノナちゃんを責めているわけじゃない」
ユーリ「そーだよー」
ノナ「だいじょうぶ……大丈夫です $\NONA$」
僕「じゃあ、話を戻すよ。この二つの三角形は合同といえる。それはなぜかというと、 この二つの三角形はぴったりと重ね合わせることができるから」

ユーリ「ねーねー、ちゃんと重ねて確かめよーよ!」
僕「ああ、そうだね。ユーリの主張は正しい。ちゃんと重ねて確かめよう。 ぴったりと重ねることができるなら、その二つの三角形は合同であるといえる。 どうやってもぴったりと重ねられないなら、その二つの三角形は合同であるとはいえない」
ユーリ「ハサミで切るんでしょ?」
僕「そうだね。ハサミで三角形を切り出してみようか」
ノナ「トレースでもいい……いいですか $\NONAQ$」
ユーリ「トレース?」
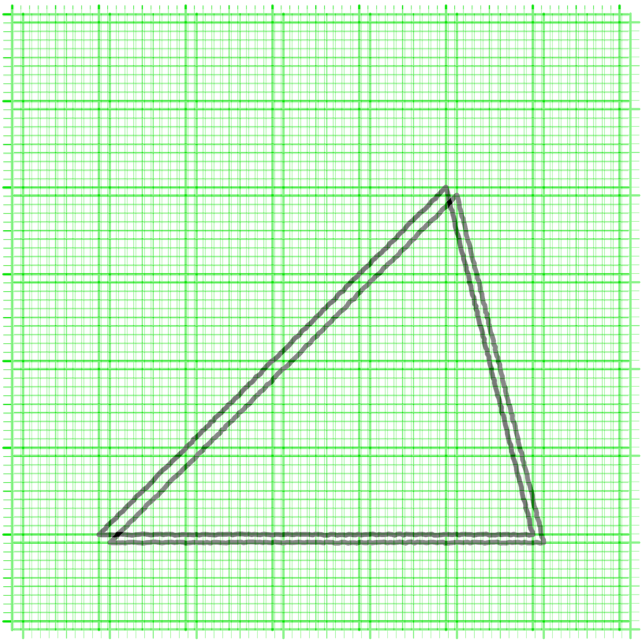
ノナは二枚のグラフ用紙を重ねて透かして見せる。
↓
↓
↓
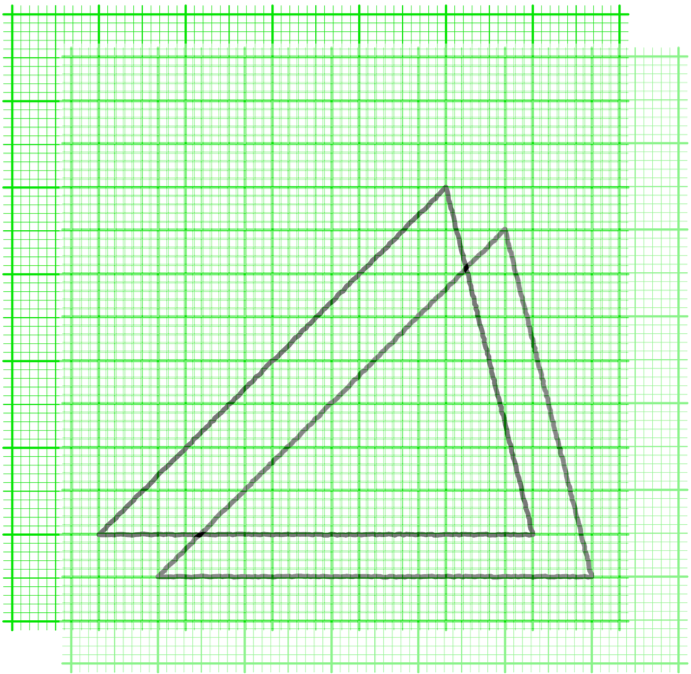
僕「うん、重ねられるね」
ノナ「ぴったり……だいたいぴったり重なります $\NONA$」
僕たちはひとしきり、グラフ用紙に三角形を描き、重ねたり透かしたりして遊んだ。
ノナ「裏返しても $\NONAQ$」
ユーリ「ねーお兄ちゃん。裏返ししても合同だよね?」
僕「うん、そうだね。二つの三角形があって、そのままではぴったり重ならないとしても、 片方を裏返してぴったり重ねられるならば、その二つの三角形は合同であるといえるよ」
この二つの三角形は、合同である。
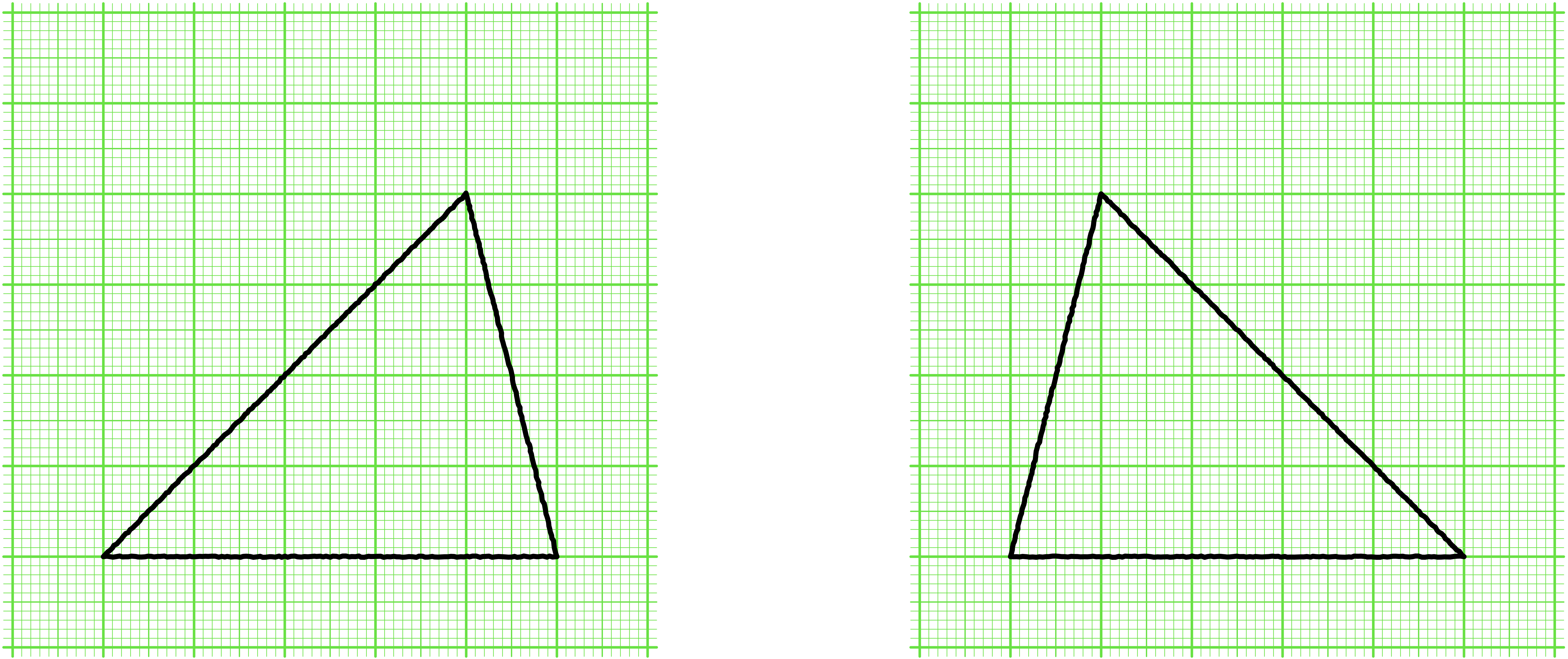
僕「いま僕たちがやったみたいに、二つの三角形を、回したり、動かしたり、裏返したりして《ぴったりと重ねる》ことができるとき、 二つの三角形は合同であるという。 でも、重ねるときに破ったり伸ばしたり縮めたりしてはだめ。 さっきは《ぴったりと重ねる》だけで済ませてしまったけれど、 ほんとうはそういうふうに補足説明が必要だったね」
ユーリ「ゆるしたげても、いいぞよ」
ノナ「いいぞよ $\NONA$」
僕「はいはい……いまは、紙を透かして重ねてみた。具体的な三角形を使うと、合同がどういうものかよくわかるね」
ユーリ「お兄ちゃんの描いた三角形、あちこち線が震えてるけどねー」
僕「そうだね。紙に描いた三角形は辺がちょっと曲がっていたり、太かったりするし、 重ねるときでもちょっとずれるかもしれない。 《現実の世界》にある三角形だから、しょうがない」
ノナ「でも $\NONAEX$」
ノナが急に声をあげたので、僕とユーリは彼女を見る。
ノナ「でも、《数学の世界》は目に見えなくても大丈夫……想像できるから、大丈夫です $\NONA$」
僕「おっと! その通りだね! ノナちゃん、いいこと言うね!」
ノナは僕の言葉に笑顔を見せる。
僕は、彼女との対話をまた思い出した。
ノナは見えるかどうかをすごく気にするんだった。
僕「ノナちゃんの言う通り、見えなくても大丈夫だね。 僕たちは便宜上、《現実の世界》の三角形を描いて考えるけれど、 僕たちが本当に考えているのは、《数学の世界》にある三角形なんだ。 目に見えている具体的な三角形だけじゃなくて、 描かれていない三角形についても考えているし、巨大過ぎて描けない三角形についても考えている。 無数の三角形をまとめて考えることもできる。 僕たちが三角形という図形を《現実の世界》で描くとき、それはあくまで手がかりに過ぎない。 その図形で何が成り立っているのか、何が成り立っていないのかを確かめるのが大事。 だから、図形の問題は、論理の問題でもあるんだ。成り立っていることから、別の成り立っていることを導いていく。 あるいは、これが成り立つためには、何が成り立っていなくてはならないかを考える。 理由を探す。定義を確かめる。そうやって、論理的なギャップがないように……いま、早口になってた?」
ユーリ「なってた。アウト」
僕「アウトだったかあ!」
ノナ「アウト……ツーアウトです $\NONA$」
僕たちは、また笑った。
ユーリ「何の話だっけ?」
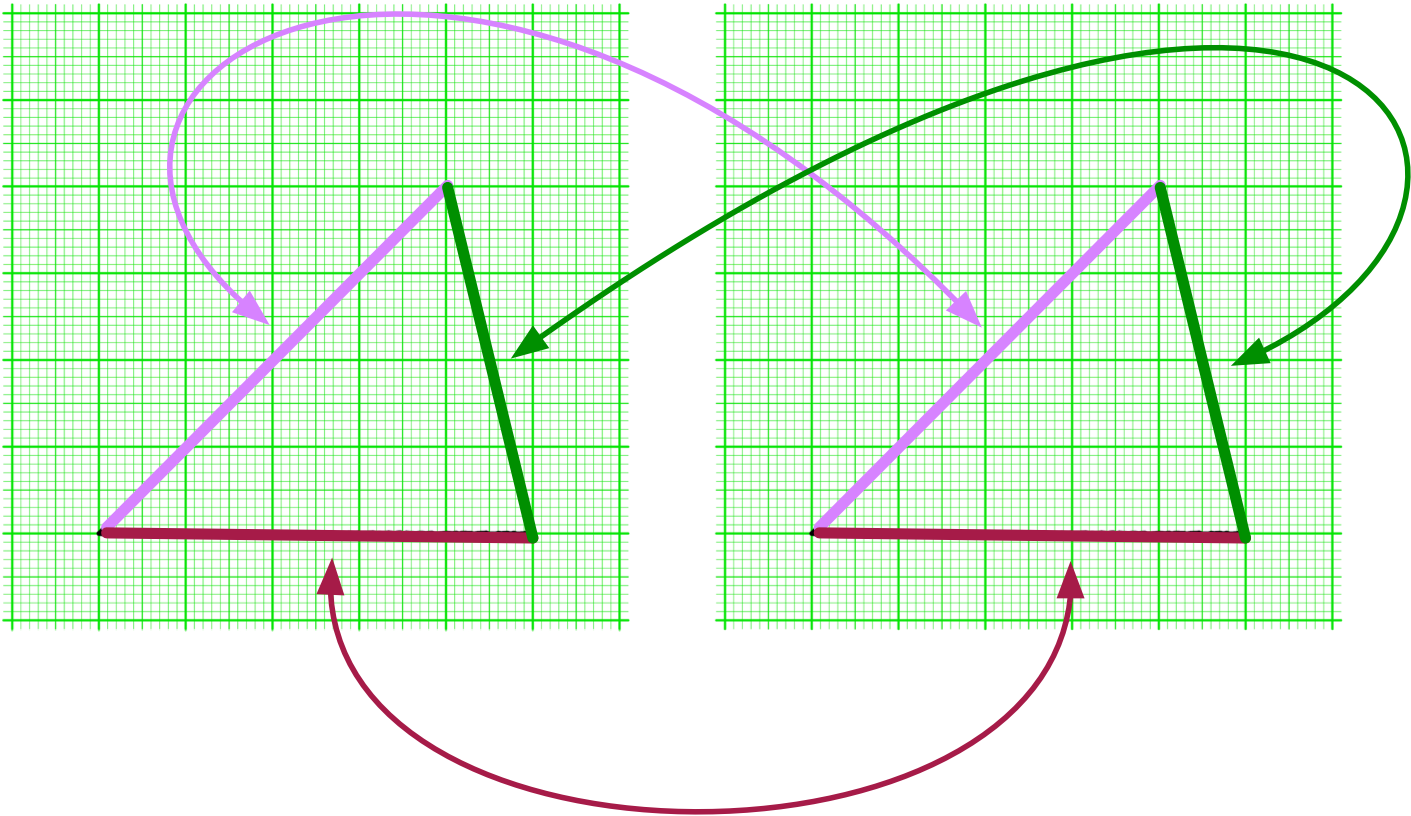
僕「二つの三角形をぴったりと重ねることができるとき、二つの三角形は合同だという……って話だね。 ところで、三角形には三つの辺と、三つの角がある。 二つの三角形をぴったりと重ねると、辺と辺、角と角もまた、ぴったり重なることになる」
ユーリとノナはいっしょにうなずく。
まるで、ぴったり重なるようにうなずく。
僕「一つの三角形に辺は三つあるし、角も三つある。三角形が二つになったら、辺も角も個数が倍になる。 たくさんあるとややこしくなるし、まちがいやすくなる。 数学では、いろんなものごとをはっきりさせて話を進めたい。 じゃあ、どうすればいいと思う?」
ノナ「$\NONAQ$」
ユーリ「簡単じゃん!」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第301回終わり)
(2020年9月18日)
この記事は『数学ガールの秘密ノート/図形の証明』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!