![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
テトラちゃん:僕の後輩。 好奇心旺盛で根気強い《元気少女》。言葉が大好きな高校生。
僕はユーリやテトラちゃんといっしょに、双倉図書館で開催されている《音楽と数学》というイベントに来ている。
いまは《純正律の輝き》コーナーで、純正律に出てくる音程について調べている。
パネルの指示に従って、 $6$ 音まで計算したところ(第287回参照)。
ユーリ「んんー、そろそろ純正律の音階、残りの $2$ 音を作ろーよ!」
僕「そうだね。ここまで作った、 $$ 1, 5/4, 4/3, 3/2, 5/3, 2 $$ という値は、 $C$ の音の高さを $1$ としたときの $6$ 音の比になるわけだよね。 楽譜に書くとどうなるんだろう」
テトラ「ハ長調($C$ major)の音階のうち $6$ 音を書いてみました」
純正律によるハ長調($C$ major)の音階($C$ を $1$ としたときの周波数比、作業途中)
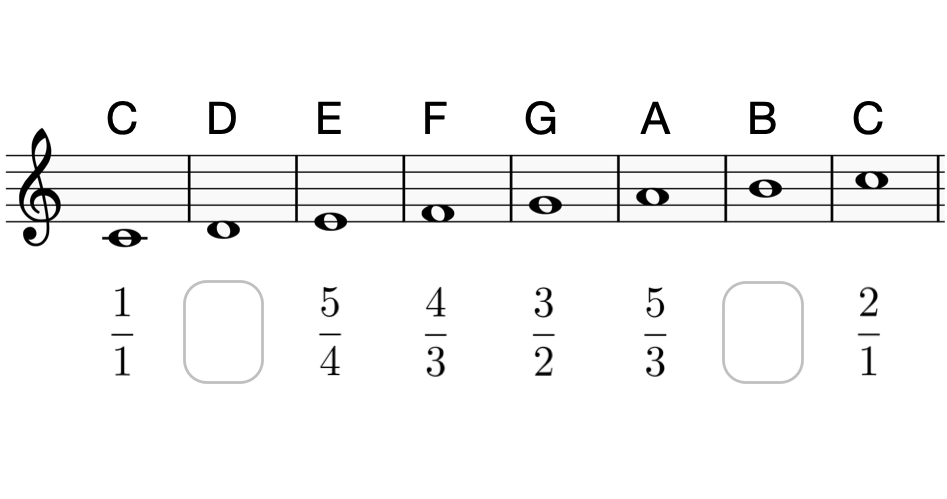
ユーリ「あいだが抜けてる」
テトラ「ユーリちゃんが言ってた『残りの $2$ 音』のところですね」
僕「他は $G$ 音を基準にして作ると書いてあったよ。このパネルによると」
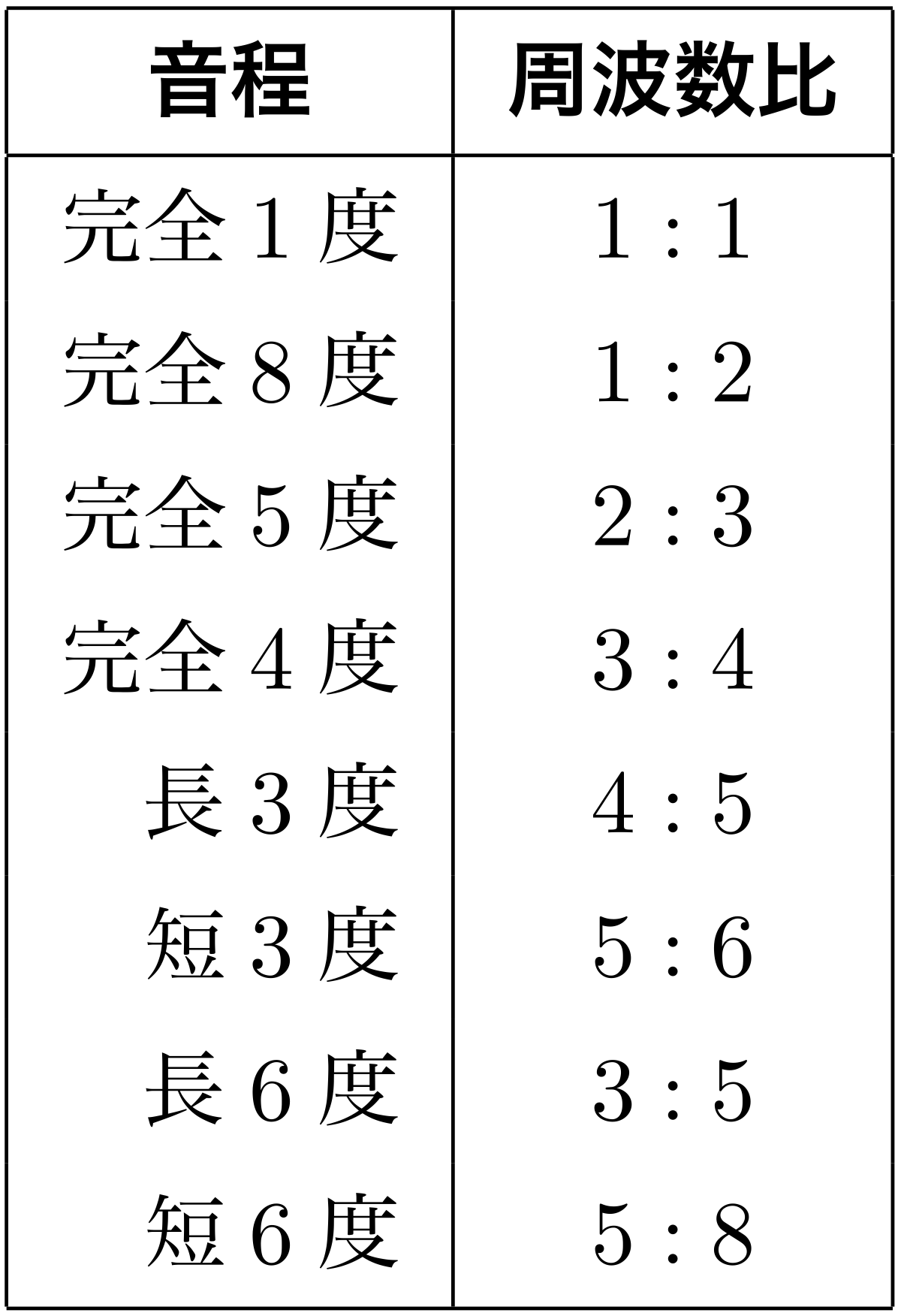
純正律による音階
この表の音程(純正音程)を使って規定された音階を純正律による音階と呼びます。
ユーリ「えーと、 $C$ Hzに対して、 $G$ Hzは、 $3C/2$ Hzだから……さらにその完全 $4$ 度下は、どーなる?」
僕「$G = 3C/2$ Hzに対して、完全 $4$ 度下の音の周波数を $x$ Hzとすると $x:G = 3:4$ ということ。つまり、 $$ x:G = x:\tfrac32C = 2x:3C = 3:4 $$ が成り立つわけだから、 $$ \dfrac{2x}{3C} = \dfrac34 $$ より、 $$ x = \dfrac{9}{8}C $$ になる。だから $C$ を $1$ とすれば、残りの $2$ 音のうち片方は $9/8$ だね」
ユーリ「残りは一つ! $G$ Hzの長 $3$ 度上の周波数を $y$ Hzとすればいーんだよね。 $4:5$ だから、 $$ G:y = \tfrac32C:y = 4:5 $$ ということで、えっと、 $$ y = \frac{15}{8}C $$ になって、 $15/8$ だ!」
テトラ「埋めてみました!」
純正律によるハ長調($C$ major)の音階($C$ を $1$ としたときの周波数比)
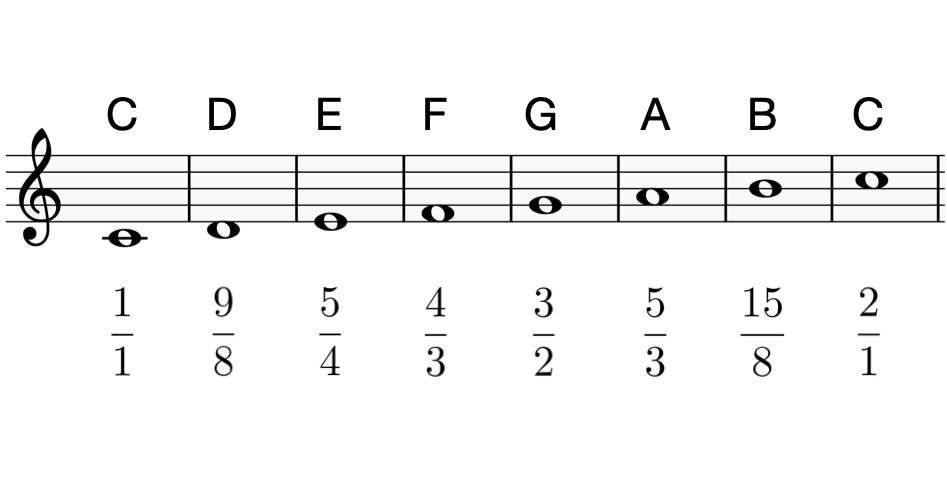
ユーリ「できたできた!」
僕たちは、パネルの指示に従って計算したこの楽譜をしばらく見つめる。
僕「……」
テトラ「……」
ユーリ「……ねえ、お兄ちゃん。気になることあんだけど、 $9/8$ とか $15/8$ って、それほど小さくなくね?」
僕「ユーリがいうのは、 $D$ の $9/8$ や、 $B$ の $15/8$ は、 $G$ の $3/2$ などに比べて《小さい整数の比》になっていないという意味だよね」
ユーリ「そーそー。小さい整数の比の方が澄んだ響きになるんじゃなかったっけ?」
僕「そうなんだけど、そこでいう《響き》は二つの音の関係だよね。 $D$ の $9/8$ というのはあくまで $C$ を $1$ としたときの周波数比。 そして $C$ と $D$ はもともと協和しない」
ユーリ「んー、そっか。 $D$ と $B$ は $G$ を基準にしたんだもんね。 あっ、だったら、 $G$ を $1$ に置き換えたら、この数字はぜんぶ変わる?」
テトラ「やってみましょう! 現在 $3/2$ になっている $G$ が $1$ になるようにするんですから、数値をぜんぶ $2/3$ 倍すればいいですね」
純正律によるハ長調($C$ major)の音階($G$ を $1$ としたときの周波数比)

ユーリ「$G$ を $1$ にすると、 $D$ は $3/4$ で $B$ は $5/4$ になるのは、そーやって作ったからわかる。 それから、もともと $G$ は $C$ の完全 $5$ 度上で作ったからそこも $2/3$ になる……」
僕「そうだね。そして $G$ を $1$ とすれば、上の $C$ は $4/3$ になる」
ユーリ「数は並べてみるとおもしろいんだね。ここでも $G$ の一つ上の $A$ は $10/9$ になって分子は二桁になっちゃう。でもそれ以外の分数は分子も文母も一桁……んー」
僕「ユーリは何を考えているんだろう」
ユーリ「あのね、ピタゴラス音律だと $2$ と $3$ しか使わなかったじゃん。 純正律だと $2$ と $3$ と $5$ を使う。それを比べたらどーなるのかなって」
僕「なるほどね! ピタゴラス音律と純正律を比較するということか」
テトラ「だったら、実際にやってみましょうよ。 純正律とピタゴラス音律の両方について、 $C$ を $1$ とした場合の周波数比を表にしてみましょう!」
純正律とピタゴラス音律によるハ長調($C$ major)の音階比較($C$ を $1$ としたときの周波数比)

僕「確かに、具体的に書いてみるとよくわかるなあ。 $C$ を $1$ としたとき、ユーリは純正律の $B$ が $15/8$ になるのを気にしていたけど、 ピタゴラス音律だと、 $243/128$ だった!(第284回参照)」
テトラ「《例示は理解の試金石》ですから、どんなときでも具体例で考えるのはいいですよね」
ユーリ「あれ……テトラさん。これ合ってる? $F$ って $4/3$ じゃなくて、もっとすごかったよーな気がする」
テトラ「そうです、そうです! こちらに書いたピタゴラス音律の $F$ は、 下の $C$ から $3$ 倍を繰り返して作ったものではなく、 上の $C$ から $1/3$ 倍で作ったものなんです。下から積み上げていくと、確か……(ノートを見返す) はい、 $F$ は $177{}147/131{}074$ になります(第284回参照)」
ユーリ「んんん……?」
テトラ「下の $C$ を $1$ 音目としてから始めて《$3$ 倍を繰り返してオクターブを越えたら $2$ で割る》のを繰り返すと、上の $C$ にたどりつけませんよね」
ユーリ「ピタゴラスコンマずれるから?」
テトラ「そうですね。そして《$3$ 倍を繰り返してオクターブを越えたら $2$ で割る》のを繰り返すと、 $F$ にたどり着くのは $12$ 音目になります。ようやく、です」
僕「そうか、 $F$ は最後に作られる音なんだ」
テトラ「なので、ピタゴラス音律で音階を作るときは通常、 $F$ を上の $C$ を $1/3$ 倍して、オクターブ内に収まるように $2$ 倍を繰り返します。 それで、 $4/3$ 倍になるんです。というのはパネルからの受け売りですけれど」
ユーリ「楽譜だと、高い低いがわかりやすいけど、これって半音と全音が混ざっているじゃん? だから、よく考えないとどこが半音でどこが全音かわからなくなるね」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2020年3月20日)