![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/ニュートン力学』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリと僕は、 『ボールを投げると放物線を描いて飛ぶのはなぜか』という疑問について議論を続けている(第271回参照)。
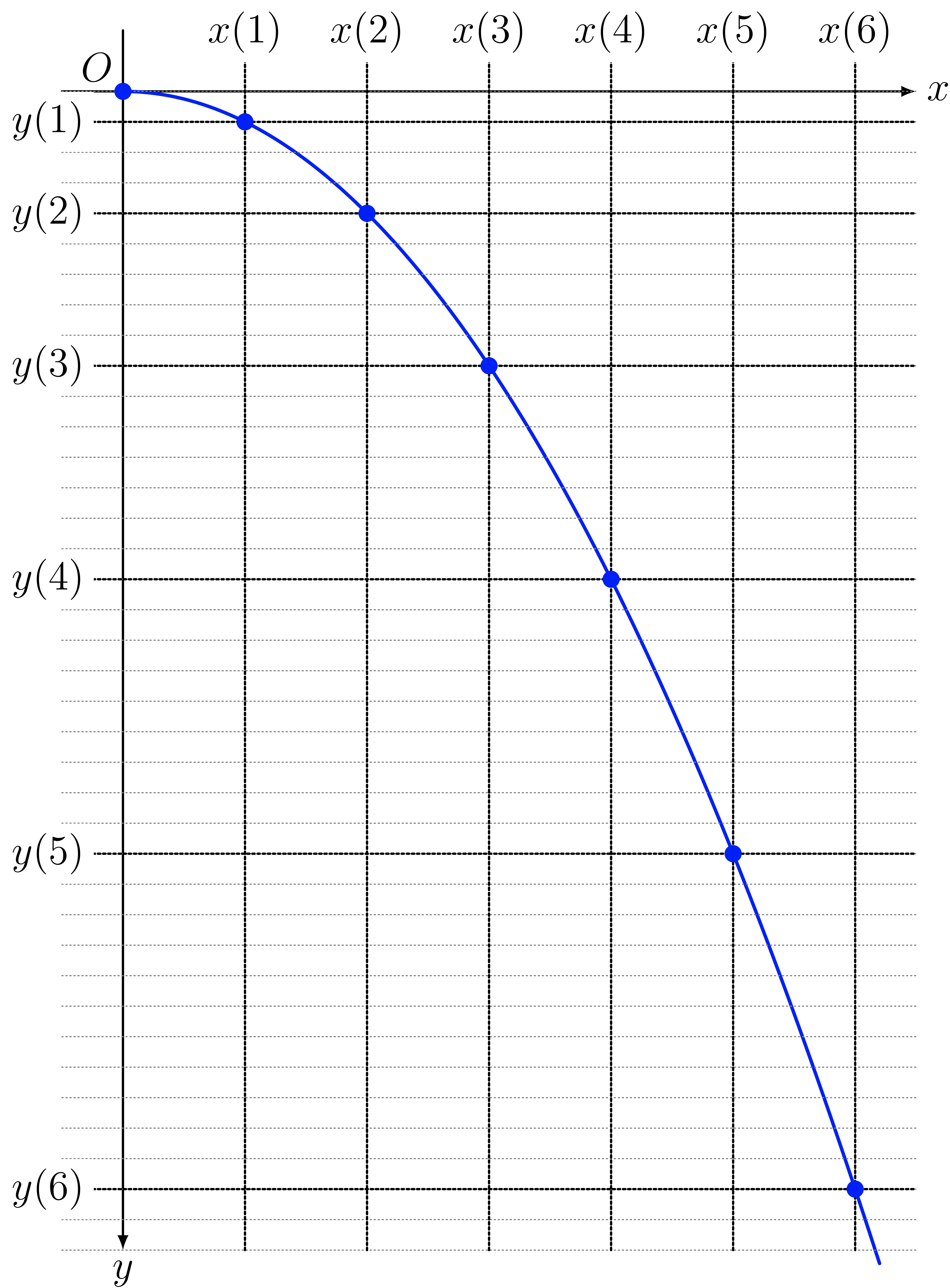
僕「ボールを質点と見なして、高いところから水平方向に投げる。質点は放物線を描いて落ちていく。 質点が動くとき、時刻 $t$ を決めれば……
・どれだけ横方向に進んだかという $x$ の値が一つ決まる。それを $x(t)$ で表す。
・どれだけ下方向に落ちたかという $y$ の値も一つ決まる。それを $y(t)$ で表す。
だから、時刻 $t$ の値が $t = 0, 1, 2, 3, \ldots$ のときに注目すると……
・ $x(t)$ の値は $x(0), x(1), x(2), x(3), \ldots$ と変化するし、
・ $y(t)$ の値は $y(0), y(1), y(2), y(3), \ldots$ と変化する。
……ここまではわかった?」
ユーリ「うん、わかった」
僕「$x(t)$ のようにカッコをつけて書いたのは、 $x$ という座標の値が時刻 $t$ の関数だ……とはっきりいうためだよ。 だから、ボールを投げたときの放物線の式を $y = ax^2$ と書いたけど、 この式は、二つの関数 $x(t)$ と $y(t)$ がどういう関係にあるかを表しているといえる」
ユーリ「どういう関係にあるか……」
僕「そうだよ。 $y = ax^2$ という等式は、《$y$ の値が $a$ と $x^2$ の積に等しい》ということを表しているよね。 特に、ボールを投げているようすと合わせて考えるなら、どんな時刻においても《$y$ の値が $a$ と $x^2$ の積に等しい》といってるわけだ」
ユーリ「ほほー」
僕「そこで、時刻のことも考えて、式の中に時刻 $t$ をはっきり書くとしたら、 $$ y(t) = ax(t)^2 $$ と表してもいいよ。どんな時刻 $t$ に対しても、 $y(t)$ の値は $a$ と $x(t)$ の二乗の積に等しいということだね」
ユーリ「うんうん、そこまではわかった。でもね、さっきから引っかかってるんだけど」
僕「何に?」
ユーリ「何だか……話がひっくり返っているみたいなの!」
僕「えっ?」
ユーリ「ひっくり返っているってゆーか、逆ってゆーか……」
僕「どういうことだろう。ユーリは、 ボールを投げたときに放物線になる理由を知りたいと思ったんだよね」
ユーリ「んー……うん、そーだよ」
僕「言葉だけで話を進めるのは難しいから、 いまは《放物線》のことを《$y = ax^2$ で表せる曲線》とした」
ユーリ「それもいーんだけど」
僕「それで、 $y = ax^2$ で表せる曲線がどんなものかを確かめている」
ユーリ「……」
僕「ボールを投げたときにどんな曲線になるかは、 本来なら実験で確かめるものだけど、 およそ、このグラフのような動きになるということがわかってる。それで、この曲線は……」

ユーリ「そこ! そこがひっくり返ってる!」
僕「へえ……どういうことだろう」
ユーリ「だってね、お兄ちゃんがやろうとしているのは、 $y = ax^2$ で表されている曲線の性質を調べることじゃん? でも、 ユーリが知りたいのは違うんだよー」
僕「うん?」
ユーリ「あのね、《放物線がどんな性質を持っているか》じゃなくて《どうして放物線になるか》という理由を知りたいんだよー。わかっておくれよー」
僕「……なるほど、なるほど」
ユーリ「理由の方を教えてよ」
僕「うん、ユーリが引っかかっていたところはわかったよ。 ユーリはきっと、もっと物理学的なことを知りたいんだね」
ユーリ「ぶつりがくてき……なこと?」
僕「うん。物理学的なこと。 もう少し絞るなら物理学の中でも特に力学の話」
ユーリ「ふむふむ……よろしい、話を続けたまえ」
僕「偉そうだな。まあ、もともと、放物線の性質を話してから、力学の話をしようと思っていたんだけどね。 ともかく、僕たちがいま考えようとしているのは、力学の中でも特に《質点の運動》と呼ばれるものだね」
ユーリ「しつてんのうんどう」
僕「そう。質点の運動。質点というのは、 質量はあるけれど、大きさを持たない点のこと。 ボールを投げるときには、本来ならば、 ボールの回転やボールが受ける空気抵抗などを考えなくちゃいけないけど、 それだと話が複雑になるから、大きさがない質点として考えてみようということ。 話を簡単にするためにね。 質量については、またあとで話すよ」
ユーリ「ふんふん」
僕「僕たちは、質点の運動を考えようとしている。 ここでいう運動というのは、 時刻ごとに位置がどうなるかのことだね」
ユーリ「動きってことでしょ? ヒューッと落ちていくみたいな」
僕「そうだね。僕たちはボールを投げたときに、 ボールが時間を掛けて落ちていくようすを見ることができる。 ストロボ撮影をすれば、時刻ごとにボールがどの位置にあるかを記録することができる」
ユーリ「……それが放物線になる」
僕「そう。ボールを質点だと思ってグラフに描くと曲線になる。 そしてそれは放物線になる。 座標軸をうまくとれば $y = ax^2$ という式で表せる曲線になるということ。 実際の実験では誤差が出るけれど、 おおよそ $y = ax^2$ という式で表せるのは確かめられる」
ユーリ「だーかーらー! ユーリが知りたいのはその理由なんだって!」
僕「あわてないでほしいな。ここからその理由の話に入るんだから」
ユーリ「むー」
僕「ここまでの話は、僕たちでも実験して確かめられる。 ボールと時計と場所を用意する。そうだ、スマートフォンで動画撮影してもいいよね。 そうすれば、時刻 $t$ ごとにボールがある位置 $(x,y)$ を求められる。 どれだけ正確な実験になるかはわからないけど、ともかくできる」
ユーリ「ふんふん?」
僕「でも、その次の一歩はものすごく難しい。とても大きな一歩になる」
ユーリ「次の一歩って?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 436本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2019年10月25日)
この記事は『数学ガールの物理ノート/ニュートン力学』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!