![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの物理ノート/ニュートン力学』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「どーして、ボールって放物線になんの?」
僕「どうして、ユーリって出し抜けに質問してくるんだろう?」
いまは土曜日。ここは僕の部屋。
いつものようにユーリが遊びにやってきて……開口一番《放物線》の質問をしてきたところである。
ユーリ「質問に質問で返すの?」
僕「そう言うユーリも質問に質問で返しているじゃないか」
ユーリ「そーゆー返しはいーから。 ねーお兄ちゃん。 どーして、ボールって放物線になんの?」
僕「どうしてって……」
僕は高校生。ユーリは中学生。
ユーリは僕のいとこだけど、 小さい頃からいっしょに遊んでいるので、僕のことをいつも《お兄ちゃん》と呼ぶ。
ユーリ「読者は聞き飽きてるよね、この紹介文。 毎回おんなじだし。 それに『小さい頃からいっしょに遊んでる』ことと『お兄ちゃんと呼ぶ』ことの論理的関係も意味不明だし。 そんなことより質問にちゃっちゃと答えてよ、お兄ちゃん!」
僕「メタな発言自重。それから地の文に突っ込むなよ。放物線がどうしたって?」
ユーリ「どーして、ボールって放物線になんの? 一言で答えて!」
僕「ユーリが言いたいのは『ボールを投げると放物線を描いて飛ぶのはなぜか』ということだよね。 いろいろ省略しすぎだろう。ボール自身は放物線にならない」
ユーリ「またそーゆー細かい突っ込み入れてくるし。そんで? ボールを投げると放物線を描いて飛ぶのはなぜかの答えは? 一言で説明して!」
僕「強いて一言で答えるなら、 水平方向には等速直線運動をして、垂直方向には等加速度直線運動をしているからというところかな」
ユーリ「……お兄ちゃん、ありがと、やっぱり説明はいいや。じゃあね、バイバイ」
ユーリは、わざとらしく帰るそぶりを見せる。
僕「ちょっと待った!」
僕は、大げさに引き留める。
ユーリ「そんな専門用語をぽんぽん出されてもわかんないよ」
僕「いいや、ユーリならわかるよ。ユーリは自分の能力にまだ気づいてないだけだ」
ユーリ「何その経験豊かな指導者口調」
僕「だってユーリは微分も積分も基本的なことはわかっているんだから、 ボールを投げたときに放物線を描くことはすぐにわかるよ。復習も兼ねて話そうか」
ユーリ「ちなみにここまでのやりとりはテンプレ」
僕「メタな発言自重。話すのやめようか」
ユーリ「話して話して!」
僕「真面目に話そう。 ユーリは『ボールを投げると放物線を描いて飛ぶのはなぜか』という疑問を出してきた」
ユーリ「うん」
僕「でも、ユーリはこのこと……つまり《投げたボールが放物線を描いて飛ぶ》ということを知ってるよね。 それなのに、どうしてまた改めて疑問に思ったんだろう」
ユーリ「いろいろ考えているうちに、何となく『あれ?』って思った」
僕「いや、その『いろいろ考えて』のところを具体的に聞きたいんだけど」
ユーリ「なんで?」
僕「だって、何か気になることがあったから疑問が出てきたんだよね。 だったら、それに沿って話をした方がスムーズになりそう」
ユーリ「ほほー……あのね。 ボールを投げたら放物線になる……放物線を描いて飛ぶってゆーのは、わかるの。 でもボールって、強く投げても弱く投げてもいいじゃん? それなのに、どんな強さで投げても放物線になるんでしょ? だとしたら不思議」
僕「なるほど」
ユーリ「それからね、ボールって高く投げたり低く投げたりするじゃん。 ほら、キャッチボールで角度をうまいこと調節して、 ぴったり相手の手元に届くように」
僕「ユーリ、キャッチボールなんて誰とやるんだ? ははーん……」
ユーリ「センサク禁止! 真面目に話してんだから」
僕「はいはい」
ユーリ「でね、どんな角度で投げても放物線になるんでしょ? それも不思議」
僕「なるほどなあ」
ユーリ「そんな感じかなー。で? 答えは?」
僕「うん、順序立てて考えてみよう。最初に放物線とはどんな形かというところを考えていこう」
ユーリ「放物線とはどんな形か……ボール投げたときの形?」
僕「いやいや、放物線のことをそう定義しちゃうと、論理的には話が終わってしまう。 ボールを投げたときにボールが描く形のことを放物線と呼ぶことにしたら、 ボールが実際にはどんな動きをしてもそれは放物線になっちゃうよね。定義上」
ユーリ「あはは! たーしかに! あはは!」
僕「妙にウケたな。話を簡単にするために、斜めに投げ上げるんじゃなくて、 水平方向にボールを投げることにしよう。 そして、それを横から見たとしよう。 そうしておいて、ボールが動くようすを描くとこんな図形になる」
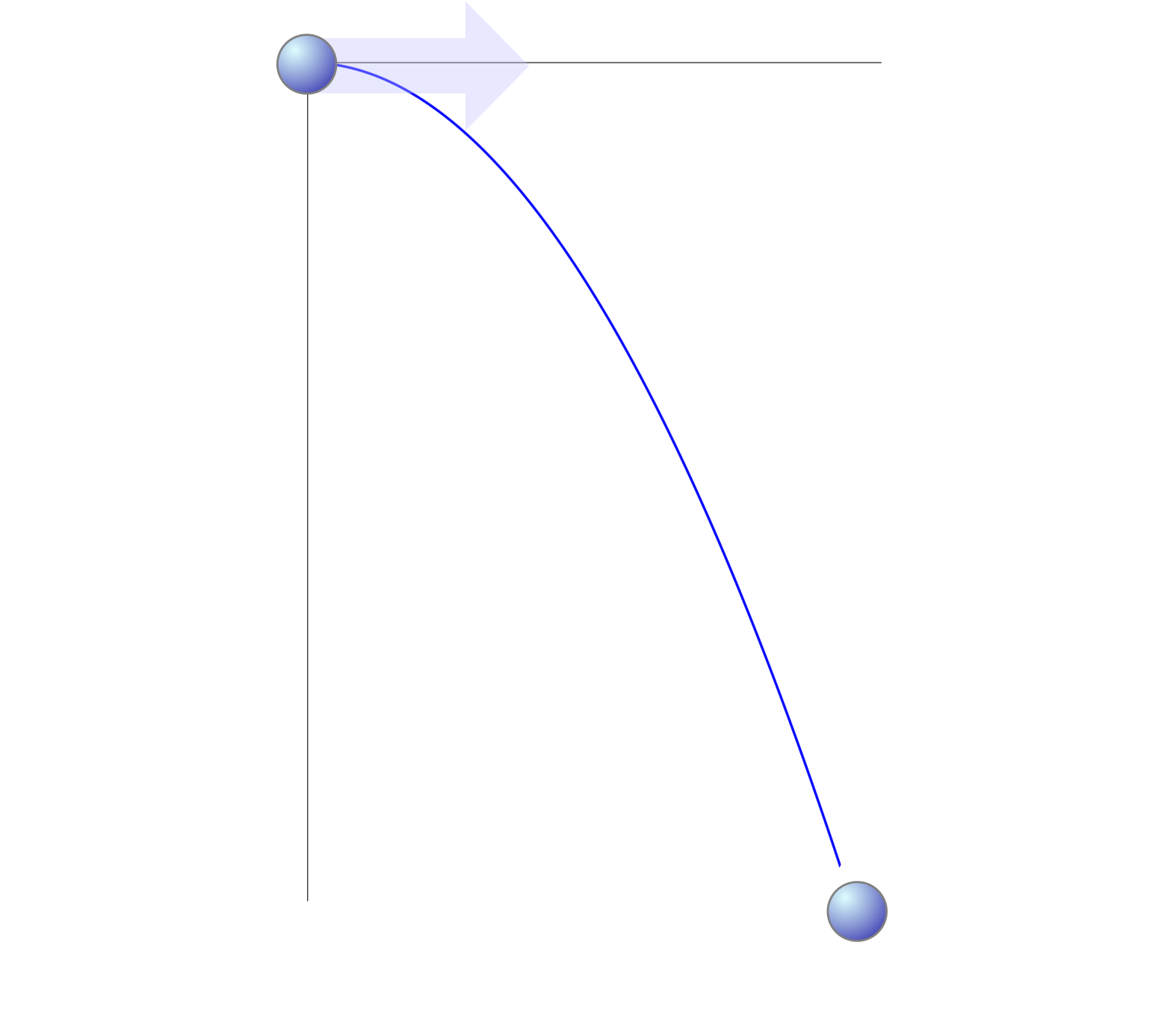
ユーリ「そだね。放物線。左上から右下にひゅーっと落ちる」
僕「グラフとして見るために、投げた場所を原点として、水平方向に $x$ 軸、垂直方向に $y$ 軸を重ねる。 いまは下に落ちていくようすを考えるから、 $y$ 軸の正の向きは下向きにしておこう。ここまでは大丈夫だよね」
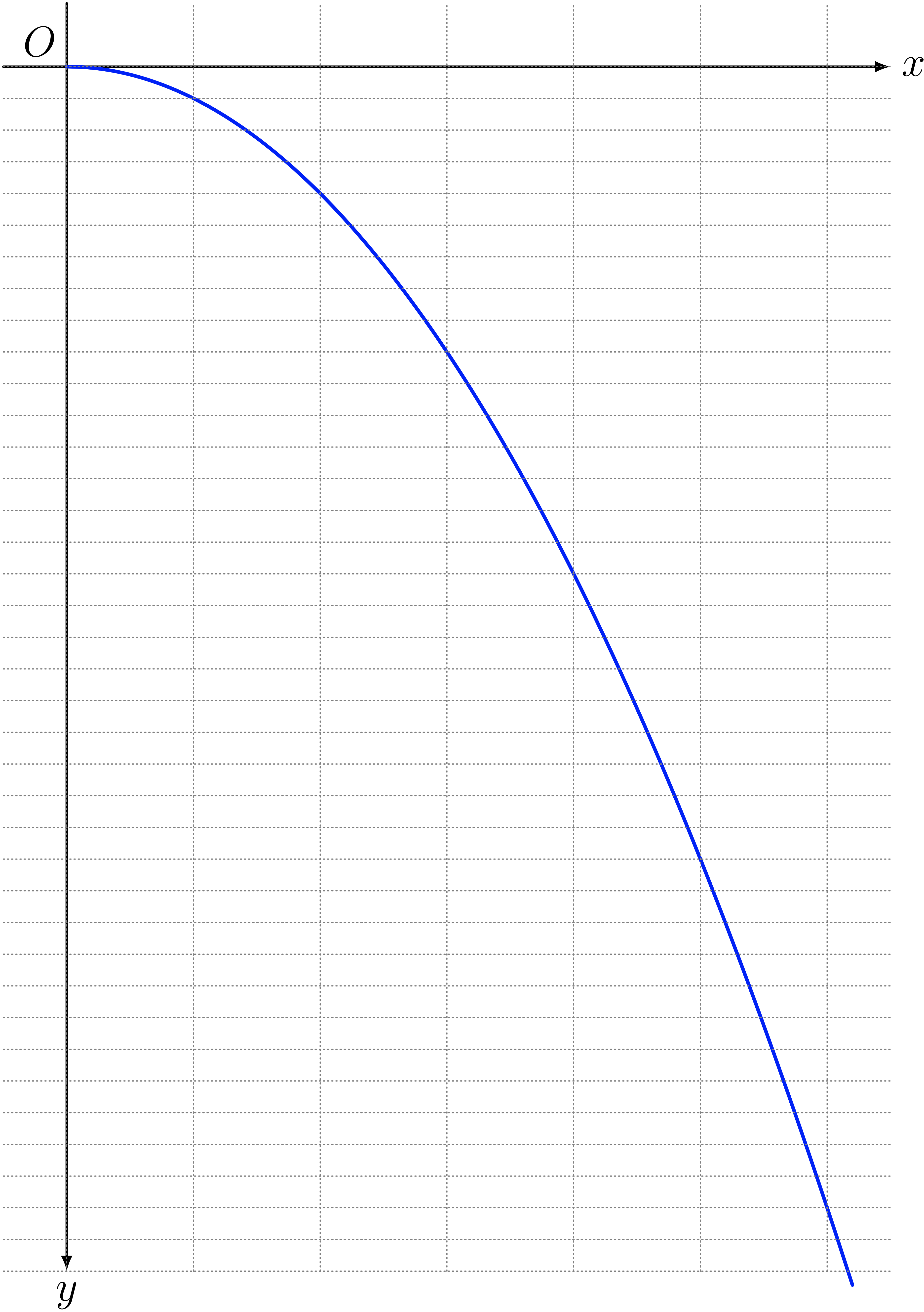
ユーリ「大丈夫だよん」
僕「グラフ上の点 $(x,y)$ に注目する。 $x$ の値を一つ決めると、 $y$ の値が一つ決まる。 このグラフ上にある点 $(x,y)$ には、 $a$ を $0$ 以外の定数として、 $$ y = ax^2 $$ という関係が成り立つ。このような図形のことを放物線と呼ぶことにしよう」
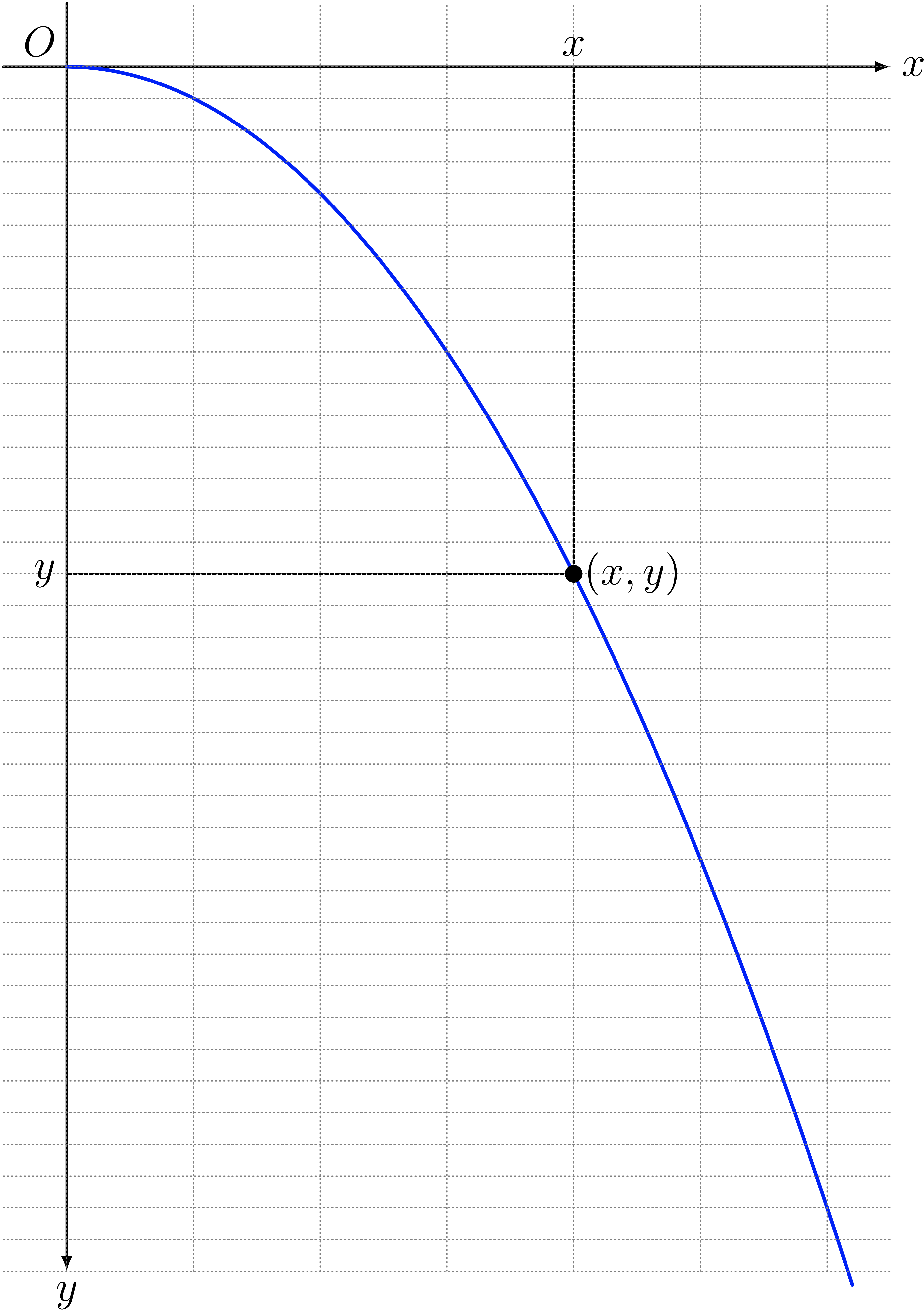
ユーリ「ふーん……」
僕「つまり、いまは、 $y = ax^2$ という式で表せる図形を放物線だと定義したわけだね。ここまで大丈夫?」
ユーリ「大丈夫だけど、なんで『いまは』なの? 明日は違う定義になるの?」
僕「『いまは……と定義する』とか『ここでは……と定義する』というのは、定義の仕方はいろいろあるけれど、 『いろいろある』では話ができないから、このように定義して話を進めるよという意味」
ユーリ「そーなんだ」
僕「たとえばさっきユーリが言ったように、『ここでは、ボールが描く形を放物線と定義する』としてもいいんだよ。 そのときには、僕たちの議論は『放物線が $y = ax^2$ で表せることを示そう』のように進むことになる」
ユーリ「は? いま何て言った?」
僕「放物線とは何であるか……その定義によって、議論の向きが変わるよといったんだ。次の(A)と(B)の違いはわかるかな?」
ここで、ユーリが沈黙の思考モードに入った。
窓からの穏やかな光を受けて、ユーリの栗色の髪が金色に輝く。
僕はユーリがこちらの世界に戻ってくるのを黙って待つ。
ユーリ「……三つあるんだね」
僕「三つ?」
ユーリ「うん。あのね。お兄ちゃんの話には、三つ出てくるの」
僕「ああ、そうだね。そう! ユーリは賢いな!」
ユーリ「そんでね、結局は(1)(2)(3)が同じだって言いたいんでしょ!?」
僕「その通り、その通り。強いて言えば、もう一つ(4)もあるね。実際に描いた《この形》のこと」

ユーリ「ほほー、にゃるほど」
僕「さて、話を戻そう。僕たちはいま(2)と(3)が同じだとした。 つまり、『$y = ax^2$ で表せる形が放物線である』と定義した。 だから、ユーリの疑問に答えるための道筋として『ボールが描く形が $y = ax^2$ で表せる』ことを示すんだ」
ここで、ユーリが再び思考モードに入る。
これはちょっと意外だった。 ユーリは論理的に考えるのが好きなので、 先ほどの『何を定義して、何を示すか』という話題に興味を持つのは理解できた。
でも、いまこの時点でユーリが引っかかるところは何だろう。 僕には想像が付かない。
静かにユーリを待つことにする。
ユーリ「……そんなの、不可能だよね」
僕「何が不可能?」
ユーリ「あのね、ボールを投げたときに描く形が $y = ax^2$ で表せることを示す……って、 不可能じゃん。だって、ほら、いろいろずれたりするし」
僕「ずれるって、誤差のこと?」
ユーリ「理科の実験でもよくあるけど、時間や長さを測るときに少しずれるの。 だから、グラフとか描いてもビシッと決まらないんだよねー。だから、 ボールが描く形が $y = ax^2$ で表せることを示すって、できなさそー」
僕「それはなかなか難しい話だなあ。 僕たちが実際に実験して何かを調べるときには必ず誤差がつきまとうのは確かだね。 どんな機械で測っても、無限の精度で測れるわけじゃない。 それに、もともと、ボールだって完全な点じゃないし。大きさがある」
ユーリ「そだね」
僕「ボールが飛んでいるとき、もしかしたら風が吹いてボールの動きに影響を与えるかもしれない」
ユーリ「台風来ているときに実験やっちゃだめ」
僕「台風まで強風じゃなくても、多少は風の動きはあるかもしれない。 でも、実験をやるのは無駄じゃない」
ユーリ「正確にバシッとわかんなくても、意味あるの?」
僕「そりゃあるよ。実験を何度も何度も行って、ほぼ同じ結果が出たならば、 その背後にある自然の法則に近づくことができるからね。 それに誤差があったとしても、その誤差がどの程度なのかがわかっていたら、 真の値はどのあたりにあるかははっきりとわかる」
ユーリ「ふーん」
僕「数学だと無限の精度でイコールだ! 等しい! といえるけど、 それはある意味、理想の状態を扱っているからだね」
ユーリ「理想の状態って、バシッと厳密に正しい状態って意味?」
僕「まあ、そういうこと。こんな見方もできるよ。 数学では、イコールを使って『これとこれがぴったり等しい』と表す。 そのように等しいと見なしたときに何がいえるかについて議論している……とね」
ユーリ「うーん……」
僕「数学的な意味で、 無限に正確な精度でボールが描く形が $y = ax^2$ で表せるわけじゃない。 でも、物理的に妥当な精度で $y = ax^2$ と見なせるかどうかを調べるのは意味がある……と、そんな感じかなあ」
ユーリ「そんで、これから何を考えんの?」
僕「うん。ボールが描く形が $y = ax^2$ になるかどうか……見なせるかどうかを調べるには、実験が要る。 そっちからじゃなくて、まず $y = ax^2$ で表せる形というのは、どういう性質を持っているかを確かめてみよう」
ユーリ「ほほー」
僕「本来なら、ここはビデオ撮りをして、ボールの軌跡を調べるところになるんだけどね。 こんな軌跡になる。一定間隔の時間で、ボールがどの位置にあるかを丸で表したわけだ」
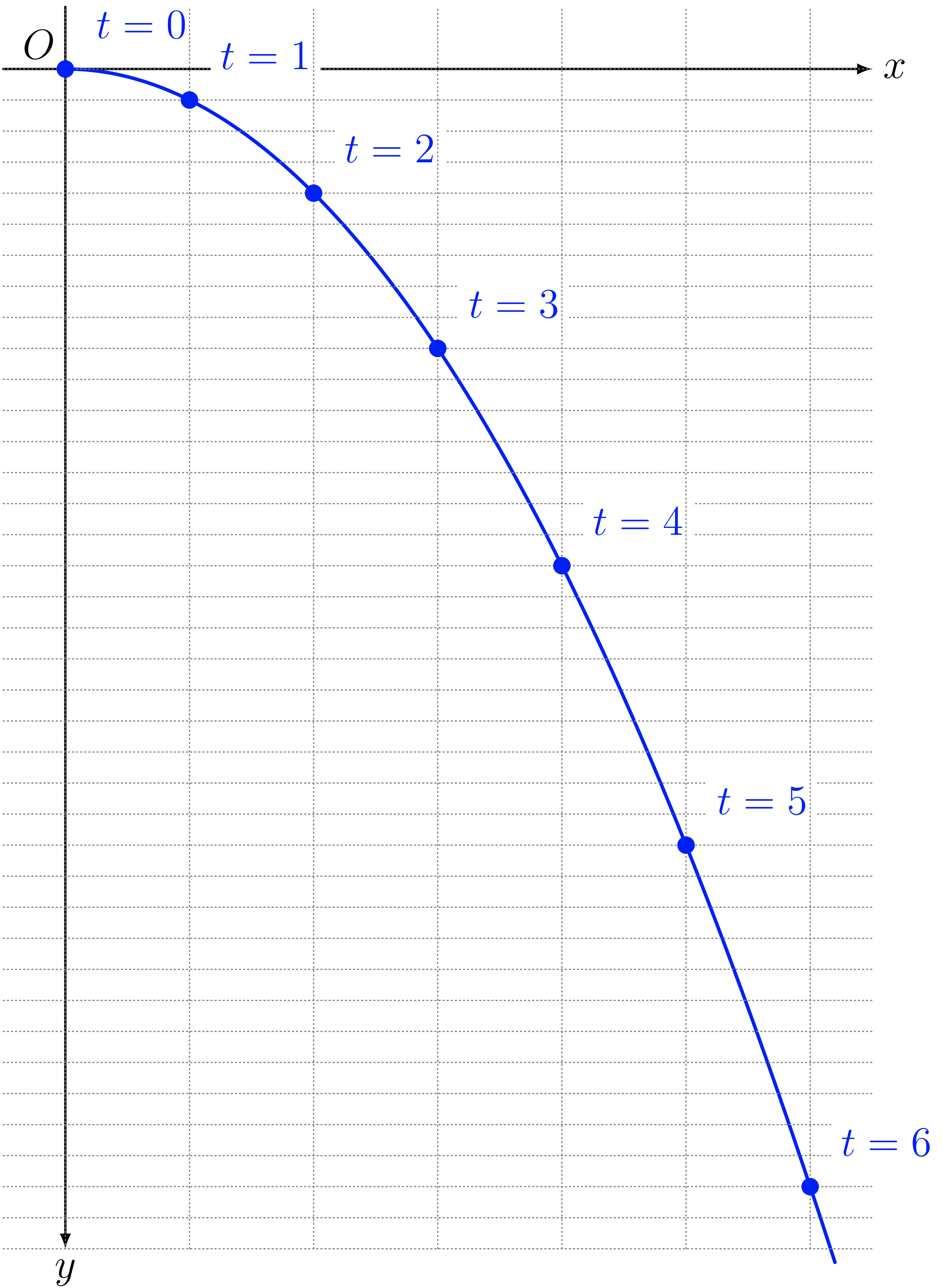
ユーリ「あ、これ、似たようなの見たよ。ストロボ……だっけ」
僕「そうだね。ユーリが言ってるのはストロボ撮影だね。実験の方法はいろいろだよ。暗いところでボールを落として、それを撮影する。 一定間隔の時間で照明を点ける。そうすると、ボールがその照明が点いたタイミングでどの位置にあるかわかる。 動画撮影するのも原理はまったく同じ」
ユーリ「ふんふん」
僕「僕たちがいま考えようとしているのは物体の運動。 物体を、質量を持った点として考えているから、質点の運動ともいう。
ユーリ「しつてんのうんどう」
僕「質点の運動を考えるときに大事なのは何だろう」
ユーリ「どんなふうに動くかが大事」
僕「そうだね。どんなふうに動くかを考えるのが、運動を考えるということだから。 ではその《どんなふうに動くか》を考えるためには、何を考える必要があるだろうか。 言い換えると、僕たちは質点の運動をどんなふうに表そうとしているだろうか」
ユーリ「何が訊かれてるのかわかんない……数式で表す?」
僕「うん、そう。数式で表す。たとえば $y = ax^2$ のような数式で表したいと考える。この $x$ や $y$ というのは、じゃあ一体何だろう」
ユーリ「ははーん、わかった。位置だ。 $x$ と $y$ で、質点の位置を表してる」
僕「その通り! 質点の運動を表すには、位置を考える必要がある。 でも、位置だけじゃ運動は十分に表せていない。他には何が必要だろう」
ユーリ「時刻!」
僕「はい、正解。質点の運動を表すには、時刻と位置がどうしても必要になる。 言い換えると、この質点が《いつ》《どこに》あるかという情報が必要になるといえる」
ユーリ「ふんふんふんふん!」
僕「質点が《いつ》《どこに》あるかをすべて言えるなら、 運動のようすがどうなっているか言えることになる」
ユーリ「ダウト!」
僕「何がダウト?」
ユーリ「だって、もしもボールの動きが $y = ax^2$ という数式で表せたとするじゃん? $x$ と $y$ が出てくるから、 位置はわかるよ。でも時刻がわかってない」
僕「ユーリは鋭い。その通りだ。まさにそれが、僕たちがいま見ている二つのグラフの違いなんだよ」
ユーリ「どゆこと?」
僕「左のグラフには $y = ax^2$ という曲線……放物線を描いた。 これは質点の運動を軌跡として表したものだけど、時刻の情報はどこにも出てこない。 ただ、 $x$ と $y$ の関係はわかっている」
ユーリ「ははあ」
僕「それに対して、一定時間の間隔で質点の位置をプロットした右のグラフには、 時刻の情報も出て来ていることになる。時刻 $t$ が $0,1,2,3,\ldots$ のときにどこにあるかがわかるからだね」
ユーリ「《いつ》《どこに》」
僕「そういうこと。だから、質点の位置をプロットした方が情報が多く含まれている」
ユーリ「……あれ、でも、 $y = ax^2$ はどーなったの?」
僕「どうなったとは?」
ユーリ「プロットしたのはいーけど、 $t$ は式のどこにも出てこないじゃん。数式に出てこなきゃ意味なくない?」
僕「そうだね。いま僕たちが見ていた、 $$ y = ax^2 $$ という式に $t$ を入れ込むとどうなるかというと、 $$ y(t) = ax(t)^2 $$ という形になる」
ユーリ「無理矢理 $t$ を入れた?」
僕「というわけじゃない。 $y = ax^2$ という式はそのままさらっと読み過ごしてしまうけど、 けっこう複雑なことを言ってる。 というのは、ここに出てくる $x$ や $y$ というのは $t$ の関数だからなんだよ」
ユーリ「どんどん話が複雑になってくにゃあ……」
僕「いやいや。 $x$ の値は、時刻 $t$ が変化するごとに変化していくよね。 時刻 $t$ を決めれば、そのときに初めて $x$ の値が一つ決まる。 そのことを、《$x$ は $t$ の関数である》という。そして $x$ を $x(t)$ という書き方をする」
ユーリ「関数 $f(x)$ なら知ってるけど……」
僕「そうだね。関数は英語でfunctionというから、よく $f(x)$ という関数が出てくる。 $f$ は $x$ の関数であるというのを、 $f(x)$ と書いている。それとまったく同じ意味で、 $x$ は $t$ の関数であるというのを $x(t)$ と表す」
ユーリ「ふーん。 $y(t)$ も同じ?」
僕「そういうこと。質点が動くとき、時刻 $t$ を決めればどれだけ落ちたかという $y$ の値も一つきまる。そのことを $y(t)$ で表す。 だから、時刻 $t$ の値が $t = 0, 1, 2, 3, \ldots$ のときに注目すると、 $x(t)$ の値は $x(0), x(1), x(2), x(3), \ldots$ と変化するし、 $y(t)$ の値は $y(0), y(1), y(2), y(3), \ldots$ と変化する」
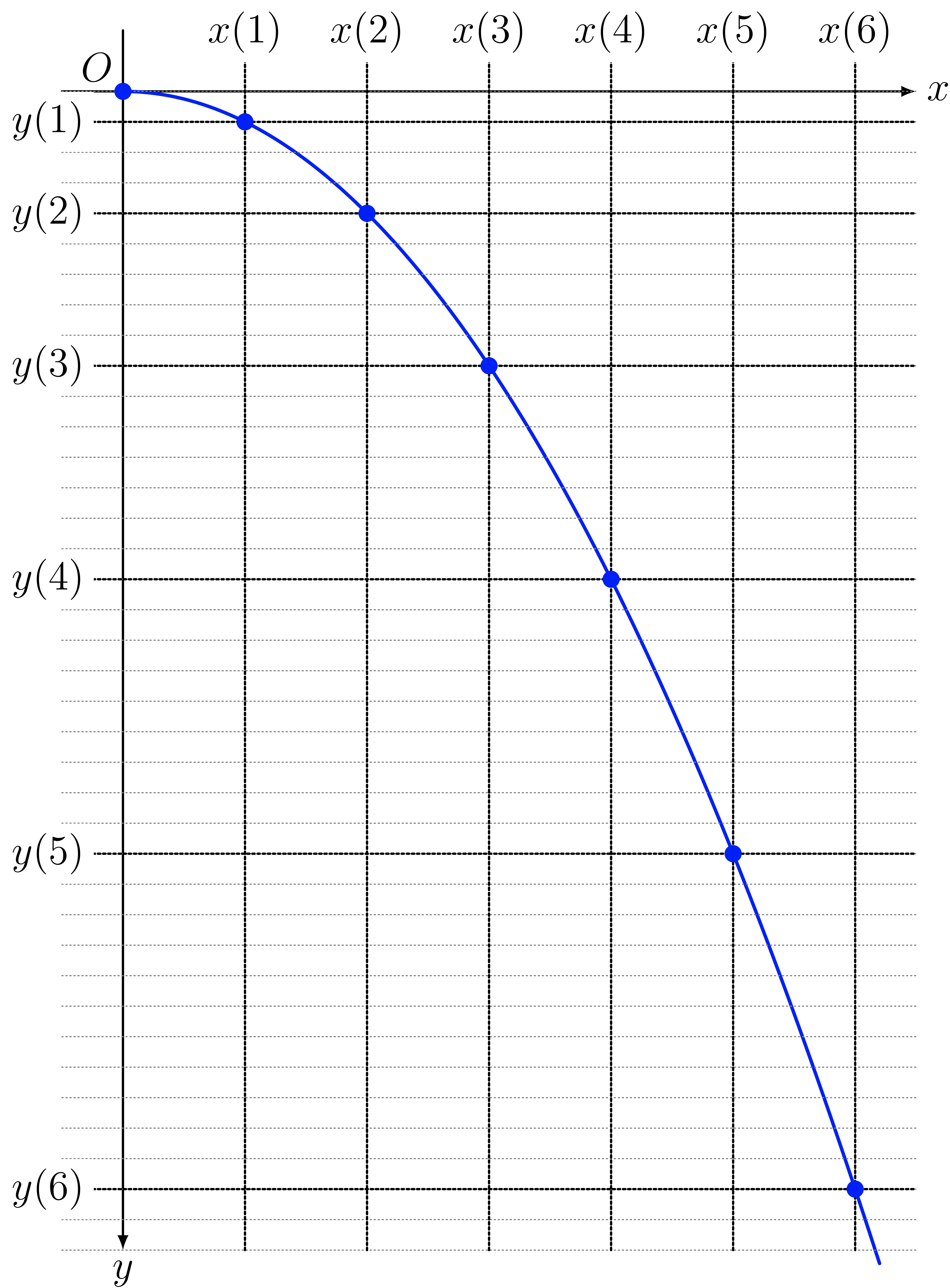
ユーリ「少しわかった」
僕「だから、 $y = ax^2$ というのは、二つの関数 $x(t)$ と $y(t)$ がどういう関係にあるかを表しているといえる」
ユーリ「何となくわかったけど、話が抽象的で難しくなってきた……」
僕「ああ、そうだね。せっかくグラフがあるんだから、具体的に考えていこう」
ユーリ「それからね……さっきから引っかかってんだけど」
僕「何に?」
ユーリ「何だか……話がひっくり返っているみたいなの!」
僕「えっ?」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第271回終わり)
(2019年10月4日)
この記事は『数学ガールの物理ノート/ニュートン力学』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!