第249回 シーズン25 エピソード9

「考える」ことの意味（前編）

リビングにて

母「ノナちゃんの『お持たせ』ですみませんけど、はいどうぞ」

ユーリ「いただきまーす！　ねーお兄ちゃん、オモタセって何？」

僕「お客さんからもらったお土産を、 そのお客さん本人のおもてなしに使うとき、 そのお土産のことを『お持たせ』っていうんだよ」

ユーリ「へー……知らなかった」

ノナ「いただきます $\NONAHEART$」

母「ここのは、とっても美味しいのよ。 お母様にもよろしくお伝えしてね、ノナちゃん」

ノナ「はい $\NONA$」

ユーリ「数学だって覚えることあるよね、お兄ちゃん」

僕「いきなり何の話？」

ユーリ「数学は暗記じゃなくて理解だぞ、ってお兄ちゃん言ってたじゃん。 でも、何にも覚えてなかったら問題だって解けないんじゃね？」

僕「ねえユーリ。 『暗記じゃなくて理解だぞ』なんて言ってないからね」

ユーリ「そーだっけ」

僕「すぐに『暗記しよう』とするんじゃなくて、まずは『理解しよう』とは言ったけど」

ユーリ「でもさー、自分が理解したことを忘れたらだめじゃん？　だから結局、覚えることはあるよね」

僕「理解して覚えるというのと、暗記……丸暗記は違うと思うよ」

ユーリ「何が違うの？　暗記を定義して議論せよ！」

ノナ「おいしい $\NONAHEART$」

僕「たとえばノナちゃんは、数式 $y = x$ がこの直線を表すことを知っている」

ノナ「覚えてる……覚えてます $\NONA$」

僕「ノナちゃんは覚えている。では、ノナちゃんは、 数式 $y = x$ がこの直線を表すということを理解しているか……」

ノナ「わからない……わかりません $\NONAX$」

ユーリ「『覚えている』と『理解している』は何が違うの？　おーい、わかんなくなってきたぞー」

僕「直線の図を見せられて、 記憶からパッと数式を取り出せるなら、 それは『覚えている』といえるよね」

ユーリ「頭ん中をググる」

僕「それはそれでいいんだけど、『理解している』としたら、もっと違うことができる」

ユーリ「とゆーと？」

僕「直線と数式の関係を理解しているなら、たとえば、こんなクイズに答えられる」

ユーリ「カンタン！　 $y = x + 1$ でしょ？」

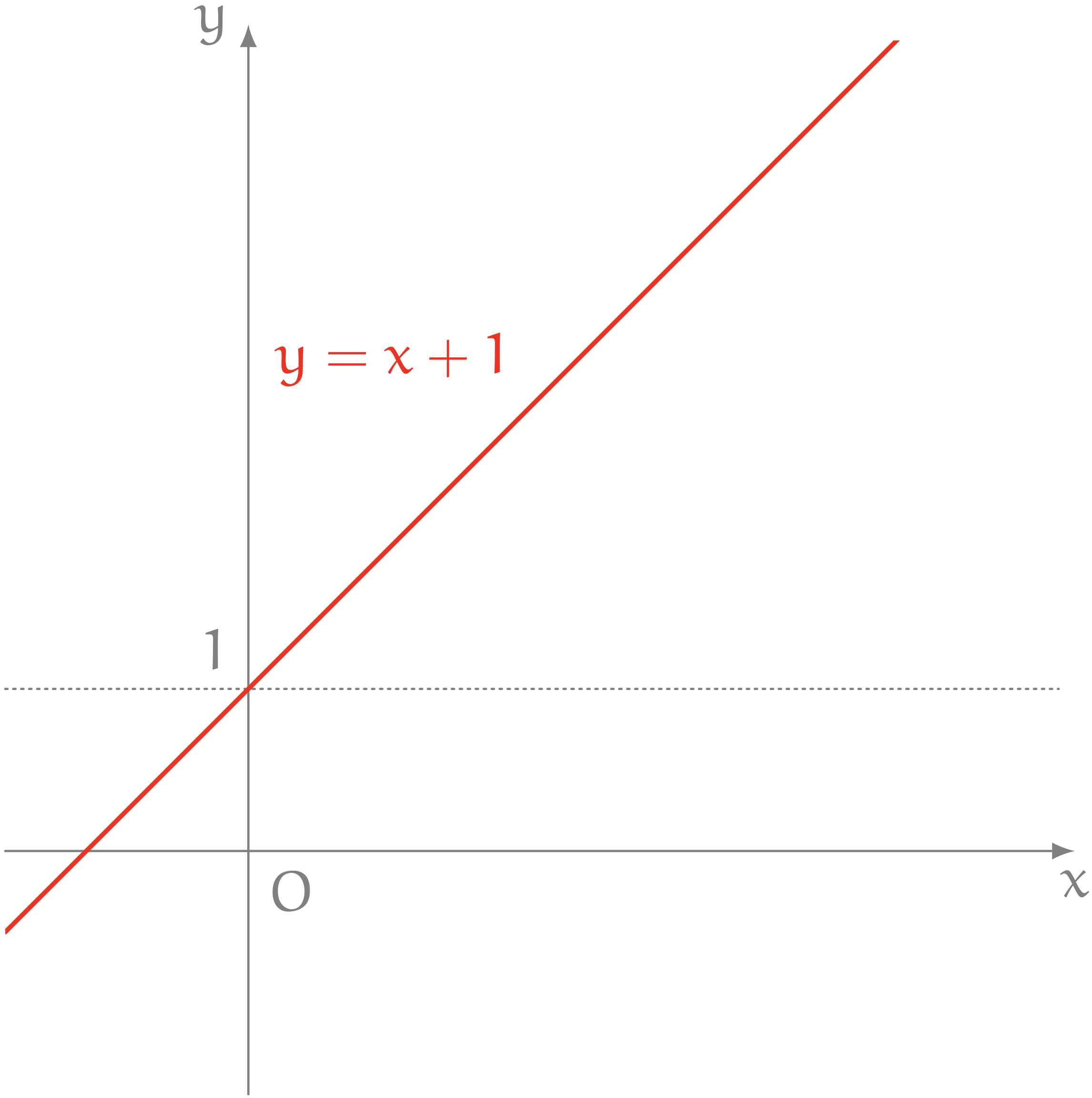
僕「ノナちゃんは、いまのクイズわかる？」

ノナ「はい……何となく $\NONA$」

ユーリ「でも、それって暗記と理解の違いなの？　クイズに答えられるかどーか」

僕「図形と数式を丸暗記してるだけだと、 $y = x$ を動かしたらどうなるかには答えられないからね」

ユーリ「いーや、そんなことはないね」

ユーリ「だってさー、 $y = x$ という直線を $1$ だけ上げたら、 $y = x + 1$ という直線になるし、 $2$ だけ上げたら、 $y = x + 2$ という直線になるし、 $3$ だけ上げたら、 $y = x + 3$ という直線になるし……ってぜーんぶ覚えている《暗記王》みたいな人がいるかもしんないじゃん？」

僕「そんな人、いるかなあ……もちろん、 一般化して覚えている人はいるだろうけど」

ノナ「$y = ax$ を $b$ だけ上げたら $y = ax + b$ になる $\NONA$」

僕「ノナちゃん、覚えてるんだ」

ノナ「暗記……暗記しました $\NONA$」

僕「暗記と理解の違いか……うん、確かにユーリの言うように、クイズのパターンをたくさん覚えたとする。 だとすると、パターンに当てはまるクイズが出てきたら、パパッと答えることができる」

ユーリ「当たり前じゃん」

僕「でも、パターンに当てはまらないクイズが出たら、まったく答えられなくなる。覚えていないから」

ユーリ「それも当たり前」

僕「仮に暗記だけして、何も理解していないとするなら、 パターンに当てはまらないクイズが出たときには、まったく答えられなくなる。 しかも、考えることすらできない。一歩も進めなくなるんだ。 覚えたパターンでしか答えられない」

ユーリ「たとえば？」

僕「たとえば、こんなクイズ」

ユーリ「どーして？」

僕「そう。どうしてそういえる？」

ユーリ「だってさー……」

僕「ちょっと待って、ユーリ。 このクイズはノナちゃんに答えてもらいたいんだけど」

ユーリ「りょーかーい」