![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png)
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート／学ぶための対話』として書籍化されています。
登場人物紹介
僕：数学が好きな高校生。
ユーリ：僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ノナ：ユーリの同級生。 ベレー帽をかぶってて、丸い眼鏡を掛けていて、ひとふさだけの銀髪メッシュ。 数学は苦手だけど、興味を持ってる中学生。
僕は、数学が苦手なノナに座標平面と直線の話をしている。
$y = x$ という式が表している直線
僕「この直線にはだいぶ慣れてきたから、別の問題に挑戦してみよう。いっしょに考えてみようね！」
ノナ「はい $\NONAHEART$」
ユーリ「いっしょに考えよー！」
僕「じゃあ、今度は $y = x$ という直線じゃなくて、別の直線を描くよ。たとえば、 $y = 2x$ という式はこんな直線を表しているといえる」
$y = 2x$ という式が表している直線
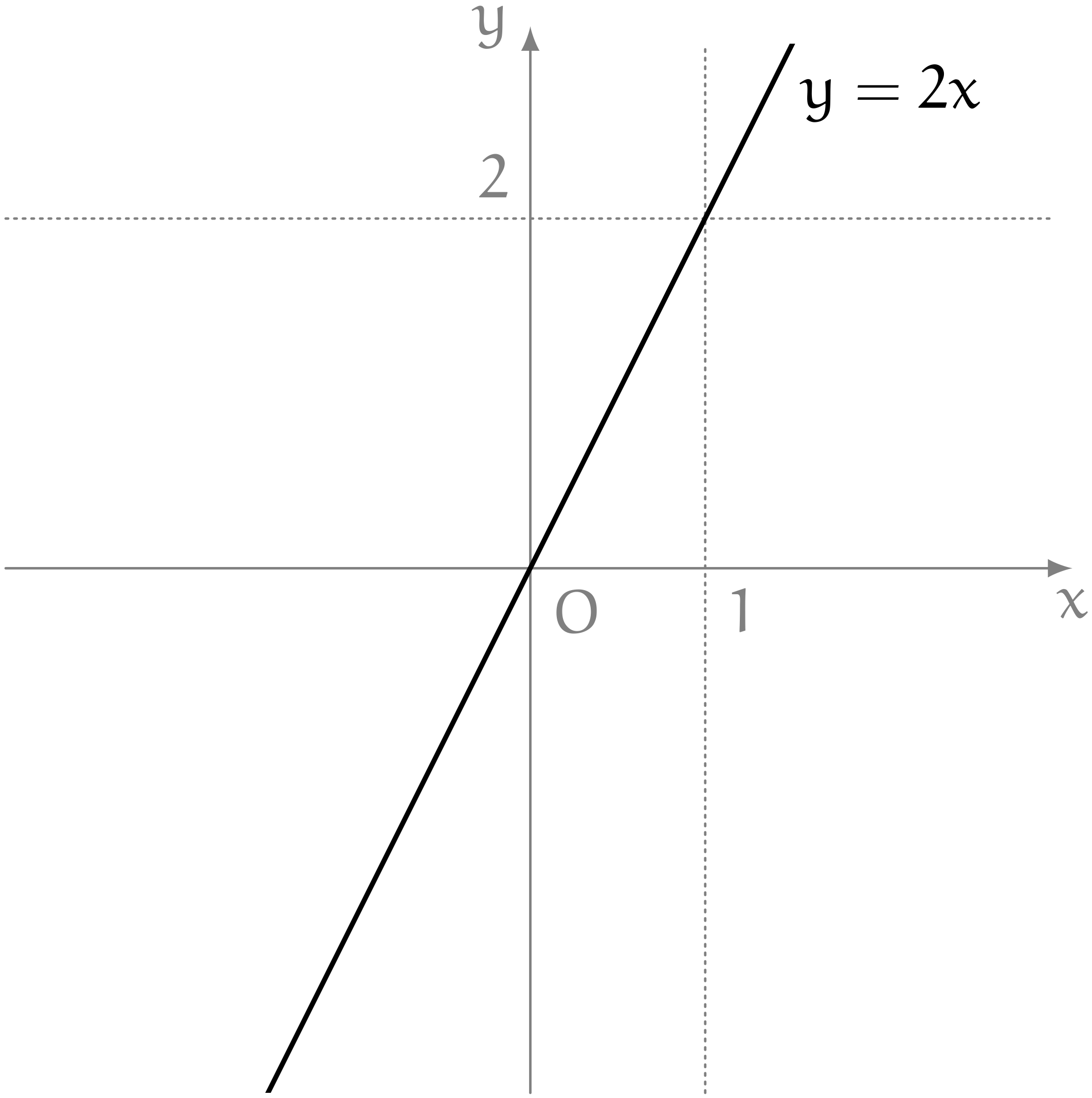
ユーリ「カンタン、カンタン！」
僕「ノナちゃんは、わかる？」
ノナ「覚えてる……覚えています $\NONA$」
僕「覚えてるんだ。 $y = ax$ という式が表す直線を覚えているのかなあ」
ノナ「$y = ax$ は光みたいなの……遠くからの光みたいです $\NONA$」
僕「遠くからの光みたいって、どういうこと？」
ノナは、ささっと紙の上に線を描いた。
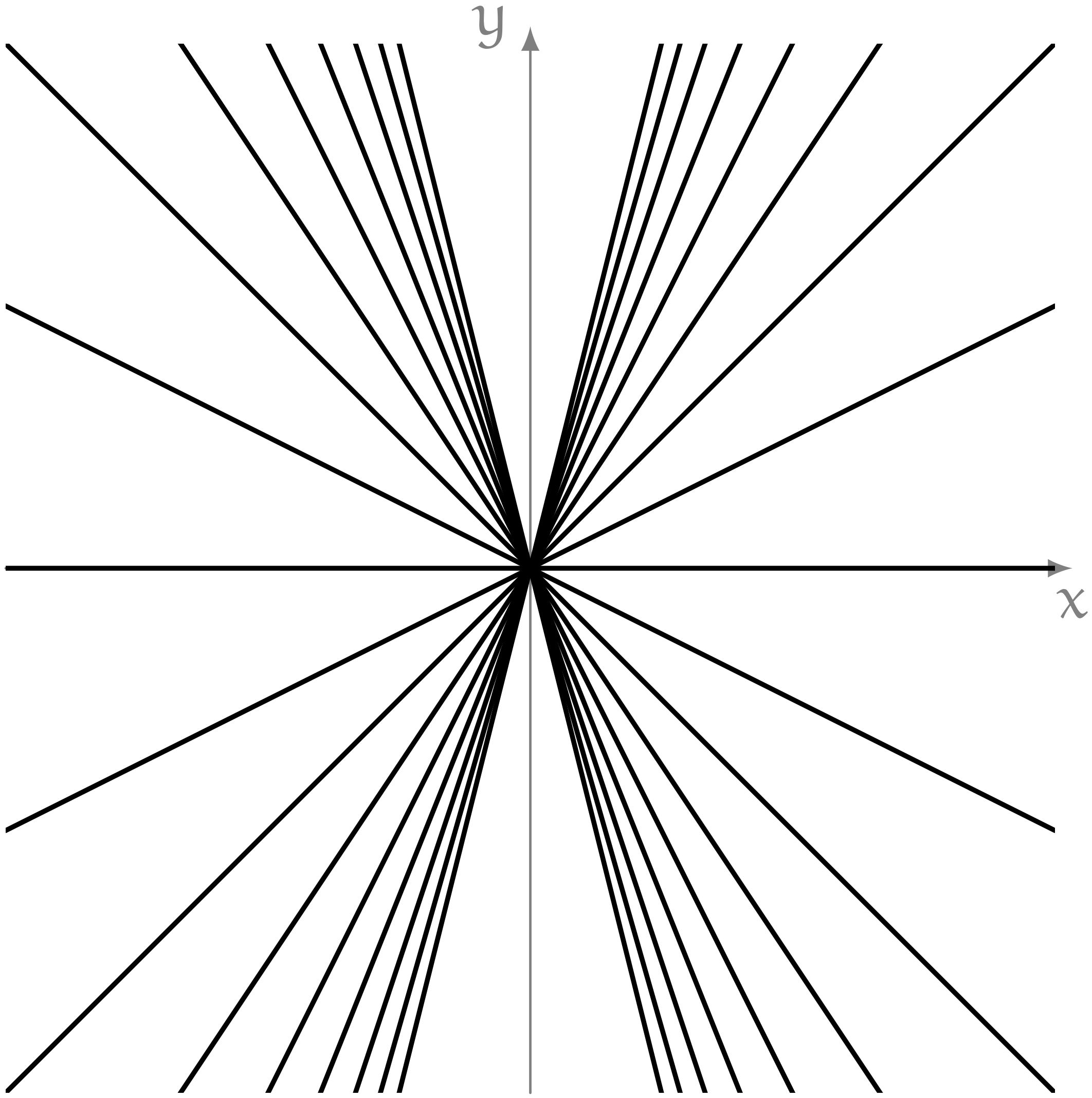
ユーリ「なーるほどー」
僕「遠くからの光か……これは $a$ の値を変えてたくさんの直線を描いたんだね。 $y = ax$ という一般的な形で」
ノナ「教科書に載ってた……載っていました $\NONA$」
僕「そこまでわかっているなら、話は早いよ。ノナちゃんはしっかりわかってる」
ノナ「ちゃんと覚えてるし $\NONA$」
僕「さっきの直線 $y = 2x$ に戻るけど、 $y = 2x$ という式は、 $2x = y$ と書いても、 $2x - y = 0$ と書いても、 $x - y = -x$ と書いても同じ直線を表している……というのは、 わかる？」
どの式でも同じ直線を表している
$$ \begin{align*} y &= 2x \\ 2x &= y \\ 2x - y &= 0 \\ x - y &= -x \\ \end{align*} $$
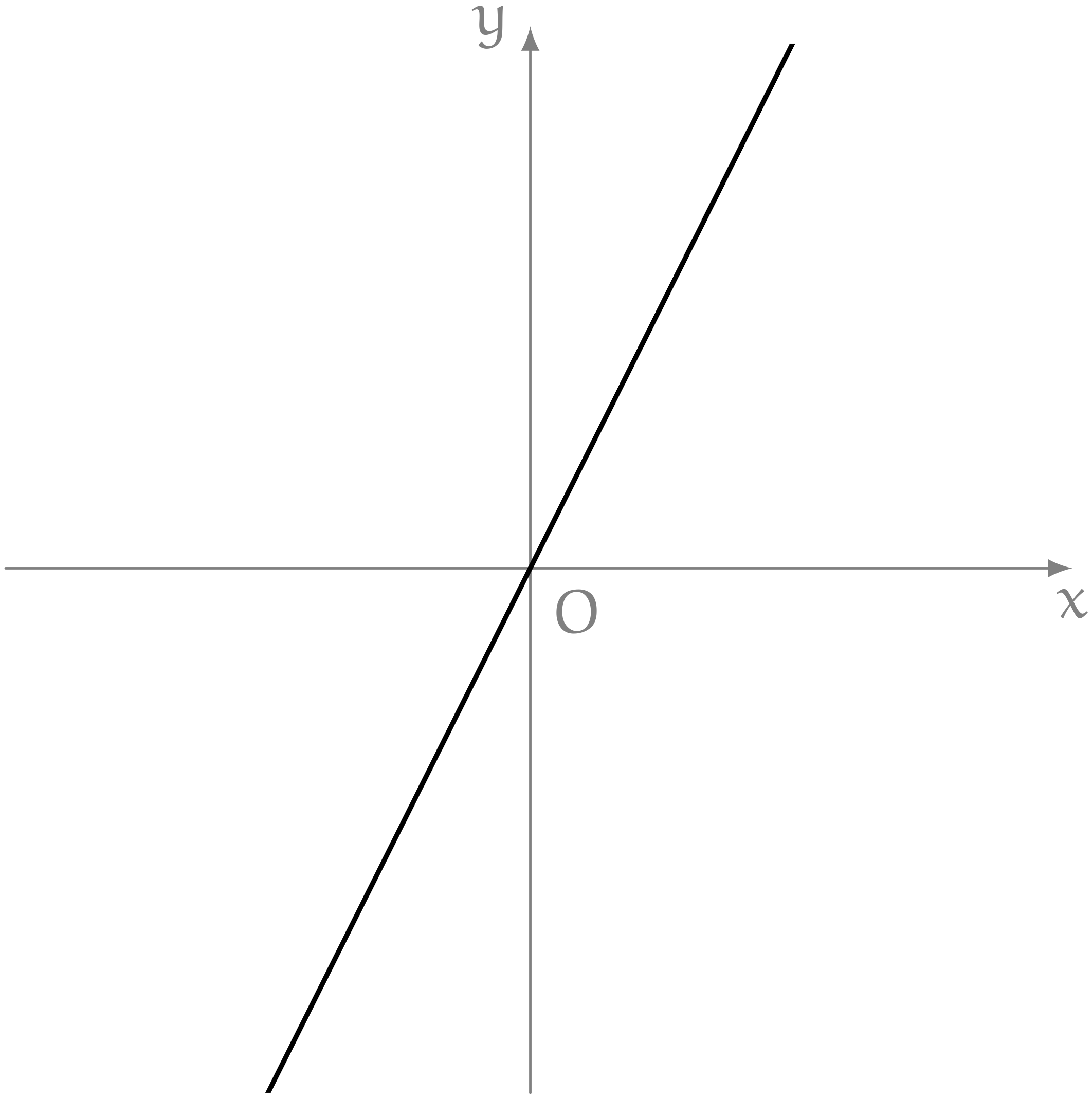
ノナ「…… $\NONAQ$」
僕「あれ？」
ユーリ「移項すればいーんでしょ？ あたりまえじゃん」
ノナ「うーん $\NONAX$」
ノナは、ベレー帽からのぞいている前髪をいじり始めた。
不思議だ。
$y = ax$ が、原点を通る一般的な直線だとわかっているのに、 $y = 2x$ という式を変形しただけで同じ直線を表すとわからなくなる？
そんなこと、あるのかな。
ノナが何を理解していて、何を理解していないか、どうもとらえどころがない。
ノナの返事も要領を得ない（というか、そもそも言葉が少ない）。
でも、ときどき「ものすごく理解してる」ような印象がある。
不思議だ。
さてさて……
ユーリ「ノナ、ノナ。 $y = 2x$ で両辺入れ換えたら $2x = y$ じゃん。だから同じなんだよー」
ノナ「それはわかる $\NONA$」
ユーリ「$2x = y$ で、 $y$ を左辺に移項したら $2x - y = 0$ になるからこれも同じだし。ノナ、移項はできてたじゃん」
ノナ「移項は覚えてるよう $\NONA$」
僕「だったら、ノナちゃんはどこで引っかかっているんだろう」
ノナ「ぜんぶ……ぜんぶわかりません $\NONA$」
ユーリ「いやいやいや」
僕「いやいやいや」
ノナの「ぜんぶわからない」発言に対して、ユーリと僕は声をハモらせながら顔の前で手のひらを振る。
練習したわけでもないのに、息がぴったり合ってるな。
僕「ねえ、ノナちゃん。 全部わからないってことはないからね。 ノナちゃんは座標平面上に点も打てるし、 $y = 2x$ という式がこの直線を表していることもわかってる。 それに $y = ax$ という一般的な直線のこともわかっている。 だから、全部わからないってことはないんだよ」
ノナ「ごめん……ごめんなさい $\NONAX$」
僕「いや、怒ってるわけじゃないから、謝らなくてもいいんだよ。 ノナちゃんは数学に興味があるんだよね。 だから僕は、少しでもノナちゃんが理解することの手伝いをしたい」
ノナは、こくんとうなずく。
僕「ノナちゃんが何をどのように理解しているかがわかるのは、ノナちゃん本人だけなんだよ。 だから『全部わからない』となっちゃうと困ってしまう」
ユーリ「そーそー！」
ノナ「怒ってない……怒ってないですか $\NONAQ$」
僕「怒ってなんかいないよ。 ノナちゃんが気になるところはどこだろう。 ノナちゃんは、 $y = 2x$ という式がこの直線を表していることはわかるんだよね」
ノナ「はい。覚えてます $\NONA$」
僕「それから、左辺と右辺を交換した $2x = y$ という式が同じ直線を表していることもわかる」
ユーリ「わかるよねー」
ノナ「はい……同じです $\NONA$」
僕「でも、 $2x - y = 0$ という式が同じ直線を表しているといわれると、何か引っかかる？」
ノナ「たぶん……同じです $\NONA$」
ユーリ「同じだよー」
僕「うん、ユーリちょっと待って。ノナちゃんは、 $2x = y$ で右辺の $y$ を左辺に移項したら $2x - y = 0$ になることは納得してる？」
$$ \begin{align*} 2x &= y && \REMTEXT{直線の式} \\ 2x - y &= 0 && \REMTEXT{右辺の$y$を左辺に移項して得られた式} \\ \end{align*} $$ノナ「大丈夫……大丈夫です $\NONA$」
僕「それなのに、 $2x = y$ という式と、 $2x - y = 0$ という式とが、同じ直線を表していると納得できない……難しいなあ！」
ノナ「ごめん……ごめんなさい $\NONAX$」
僕「いやいや、テト……ノナちゃんは謝らなくてもいいよ」
ユーリ「お兄ちゃん！ いま名前まちがえなかった？」
僕「ごめんごめん。 何だか、テトラちゃんを思い出しちゃって。テトラちゃんもよく謝るんだよね、なぜか。 理解できないことを謝る必要は何もないのに」
ユーリ「ひとの名前まちがえるって、かなりヤバいよ。それは謝る必要あるよ」
ノナ「悪いから……悪いからです $\NONA$」
僕「悪いって何が？」
ノナ「すぐに答えられないのが悪いから謝るの……謝るんです $\NONA$」
ユーリ「いやいやいや」
僕「いやいやいや」
またもや、息ぴったり。
僕「すぐに答えられなくても悪いことは何一つないよ。 考えるとき、時間はたっぷり掛けていいんだ。もちろんテストなんかは困るけど、 ふだん数学を考えるときには、時間はたっぷり掛ける。 だって、僕たちが学んでいる数学はめちゃめちゃ頭がいい数学者たちが、 とんでもなく長い時間を掛けて考え抜いてきたものなんだよ」
ユーリ「早口」
僕「おっとっと……それでね、そんな数学を僕たちは学ぼうとしている。 『ぱっと聞いて、さっと答える』ことよりも、 『ゆっくり聞いて、じっくり考えて、しっかり答える』ことが大事なんじゃないかなあ」
ノナ「移項しても答えが出ないから……出なくてもいいんですか $\NONAQ$」
僕「はい？」
ノナ「$2x = y$ で $2x - y = 0$ だと $x = $ にならない……なりません $\NONAX$」
難易度高いなあ……と僕は思う。
ノナの言葉を読み解くのはすごく難しい。そして、もどかしい。
でも、 ノナは支離滅裂なことを言ってるわけではないように見える。
彼女の中には一貫した考え方が何かあるように思える。
難易度が高いと感じるのは、 ノナの考え方が僕やユーリとずいぶん違うからだ……たぶん。
ノナがどう考えているかを探りたい。
彼女が何に引っかかっているのかを確かめたい。
彼女がどう考えているのかを解きほぐしたい。
でも、その手がかりはノナの頭の中に隠されていて、僕は直接それに触れることはできない。
ベレー帽の中にある頭脳の動きを彼女自身が調べて、 なんとか外に出してくれないと、 手助けするのは難しい。
とても、難しい。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 440本すべての記事が読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方／すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加（2018年12月7日）
この記事は『数学ガールの秘密ノート／学ぶための対話』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ！
![[icon]](https://img.hyuki.net/20220619121014-abd58cfc2ab436f4.png)