第237回 シーズン24 エピソード7

巡り回る群れ（前編）

図書室にて

テトラ「要素が $4$ 個ある群は一種類とは限らないというのはわかりました。 ところで話を戻しちゃうんですが、 集合の要素がトランプでも、 東西南北でも、 サイコロの置き方でも、 $\sin\theta$ を微分したものでも、 $0,1,2,3$ を使ったものでも、 《同じ群》といえるんですね。 ぐるっと回ってくるところが《同じ》に感じます」

僕「もちろん、演算表も《同じ》になるね」

ミルカ「$\{1, i, -1, -i\}$ も《同じ》だな。虚数単位 $i$ が生成する群だ」

テトラ「ああ、確かに《同じ》ですねっ！」

僕「確かに、 $i$ を忘れちゃいけないなあ。これは、 $i^0, i^1, i^2, i^3$ ということだね」

ミルカ「ふむ。演算表で $1$ と $-1$ のみに注目すると、こうなるな」

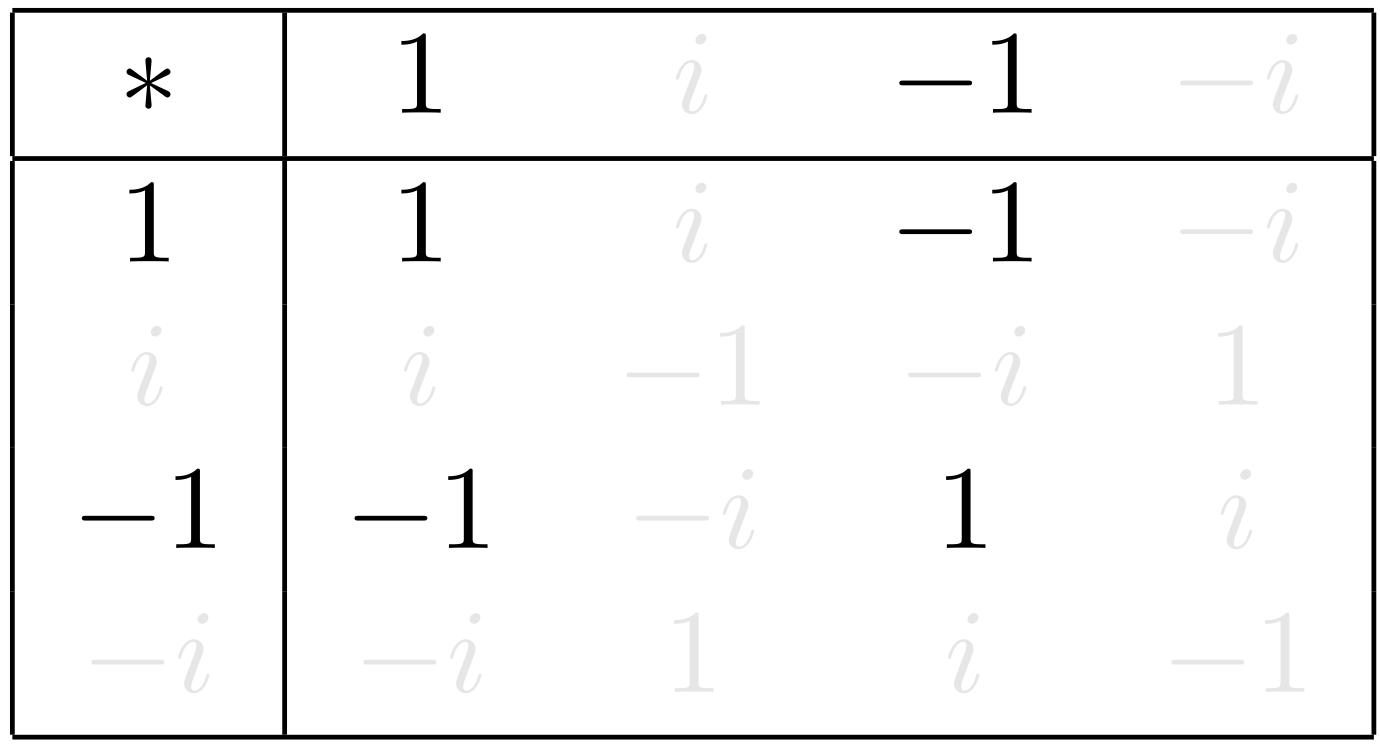
テトラ「そうですね。 $-1$ に注目すると、 $$ \begin{align*} &1 \MUL 1 = 1 \times 1 = 1 \\ &1 \MUL (-1) = 1 \times (-1) = -1 \\ &(-1) \MUL 1 = (-1) \times 1 = -1 \\ &(-1) \MUL (-1) = (-1) \times (-1) = 1 \\ \end{align*} $$ という四通りだけです」

ミルカ「$-1$ に注目するというのは、《$i$ が生成する群》の部分群を作っているともいえる」

テトラ「部分群……部分集合ですか」

ミルカ「部分群。 二項演算のことを忘れて台集合だけに注目するなら、部分集合でいい。 部分集合が同じ二項演算に対して群をなしていたら、部分群という」

↓部分群

僕「《$i$ が生成する群》はサイコロの回転でいえば $90$ 度の回転に対応して、 《$-1$ が生成する群》は、 $180$ 度の回転に対応するといえるね」

ミルカ「《$i$ が生成する群》も《$-1$ が生成する群》も、 どちらもたった一つの元から生成される群といえる。 そういう群を巡回群（じゅんかいぐん）という」

テトラ「はいはいっ！　巡って回ってくる群ですねっ！　ぐるっと回ってくる群です」

ミルカ「テトラは《ぐるっと回る》という表現が好きだな。巡回群の定義はこうだ」

テトラ「えっ！！　 これが巡回群の定義なんですか？」

僕「テトラちゃんは何に驚いているの？」

テトラ「サイコロの回転でも、 $i$ の積でも、《ぐるっと回る》イメージがありました。 でも、この巡回群の定義には《ぐるっと回る》イメージは何もありませんよね……だって、 この定義では、どの元 $a$ も、 $$ a = g^n $$ と表せるとしか言っていませんから。これで《ぐるっと回る》というイメージの群になるんでしょうか」

僕「定義には出てこないけど、よく考えるとそのイメージは出てくるよ」

ミルカ「……」

テトラ「ちょちょっ、ちょっとお待ちください。いまテトラの中では《わかってない注意報》が鳴ってます！」

ミルカ「テトラは、自分が抱いた疑問を明確に述べる」

テトラ「えっと……あたしは、群の定義を理解していたつもりでした。 台集合と二項演算、単位元に結合法則に逆元を使った定義のことです。 それから巡回群についても以前お聞きして、何となくわかっていました。 《$i$ が生成する群》を見ながら、確かにぐるっと巡り回ってくる巡回群だと思っていました。 でも、ミルカさんの巡回群の定義からは《ぐるっと回る》イメージは出てきません。それが腑に落ちない点です」

ミルカ「君は、テトラの疑問に適切な問いかけを投げる」

僕「《適切な問いかけを投げる》って……ねえ、ミルカさん。 ミルカさんは最近、そういうメタ・アドバイスをよく言うよね。 その一言でハードルがいきなり上がるんだけどなあ」

ミルカ「ハードル上げが、ひそかなマイブーム」

テトラ「あの、それで……」

僕「うん、テトラちゃんの言う《ぐるっと回る》イメージを群の言葉で表すとしたらどうなると思う？」

テトラ「《ぐるっと回る》イメージを群の言葉で表す……」

僕「たとえば」

ミルカ「ヒント早すぎ」

テトラ「大丈夫です」

テトラ「ヒントはなくても大丈夫です。 あたしが思い描いている《ぐるっと回る》イメージを、群の定義に出てくるような数学的表現を使って表すということですね」

僕「そうそう」