第222回 シーズン23 エピソード2

瞬間の速度（後編）

《平均の速度》から《瞬間の速度》へ

ユーリ「早く《瞬間の速度》を定義してよ！」

僕「うん、いっしょに考えていこう。僕たちが考えている状況……その舞台設定はこうだよ」

ユーリ「だいじょぶ」

僕「それから、《瞬間の速度》を定義するために僕たちが使う道具は《平均の速度》だね」

ユーリ「これも、だいじょぶ」

僕「そして、僕たちは時刻 $t_0$ という瞬間、その《瞬間の速度》として $v_0$ を定義したい。 僕はその定義を知ってるけど、それをどーんと出しちゃつまらないから、ユーリといっしょに考えたい」

ユーリ「別にどーんと出してくれてもいーんだけどね。お兄ちゃんに付き合ってあげよー！」

僕「さてと、時刻 $t_0$ における《瞬間の速度》$v_0$ は、こんな不等式を満たしてほしいなと思う。 きちんとした説明はあとでまた話すけど、まずは不等式のところだけ書いてみよう」

ユーリ「出たな、謎の不等式」

僕「でも、数式をちゃんと読めば、この不等式は何を表しているかわかるよね、ユーリ。たとえば、 $v_0 - \EPSLN$ は何だろうか」

ユーリ「$v_0 - \EPSLN$ は、ちょっと小さいってことでしょ？」

僕「『ちょっと小さい』って、何が・どれだけ・何よりも小さいの？」

ユーリ「あー、 $v_0 - \EPSLN$ は、時刻 $t_0$ の《瞬間の速度》$v_0$ より $\EPSLN$ だけ小さい」

僕「そうだね！　同じように、 $v_0 + \EPSLN$ は、時刻 $t_0$ の《瞬間の速度》$v_0$ より $\EPSLN$ だけ大きい」

ユーリ「あと、真ん中は時刻 $t_0$ から時刻 $t_1$ までの《平均の速度》」

僕「その通り！　 この不等式は《平均の速度》が《瞬間の速度》に近いことを表している。 どのくらい近いかというと $\EPSLN$ 以上は離れないくらい近いということ」

ユーリ「へ？　そうなる？」

僕「そうなるよ。 $v_0 - \EPSLN$ と $v_0 + \EPSLN$ の間に《平均の速度》が入るってことだから。 こんなふうに数直線上で表してみると大小関係がはっきりするよね。《平均の速度》は $v_0$ より小さいか、大きいかはわからないけど、 でもとにかく $\EPSLN$ 以上は離れてないよ、と」

ユーリ「そっか……」

僕「わかりにくかったら、《平均の速度》と《瞬間の速度》の引き算の形にしようか」

ユーリ「引き算した結果は $-\EPSLN$ と $\EPSLN$ で《はさみうち》する！　……ってこと？」

僕「そういうこと」

ユーリ「それから？」

僕「いま僕たちは《瞬間の速度》というものを定義したい。 《瞬間の速度》を定義するために《平均の速度》を利用する。 《瞬間の速度》というものがあったとして《平均の速度》がどれだけそれに近いかを $\EPSLN$ という正の数で見積もったともいえる。 $\EPSLN$ を小さくできるなら、《瞬間の速度》は《平均の速度》にとても近いといえる。 この不等式が主張しているのは、《瞬間の速度》と《平均の速度》が $\EPSLN$ 以上離れていないということ」

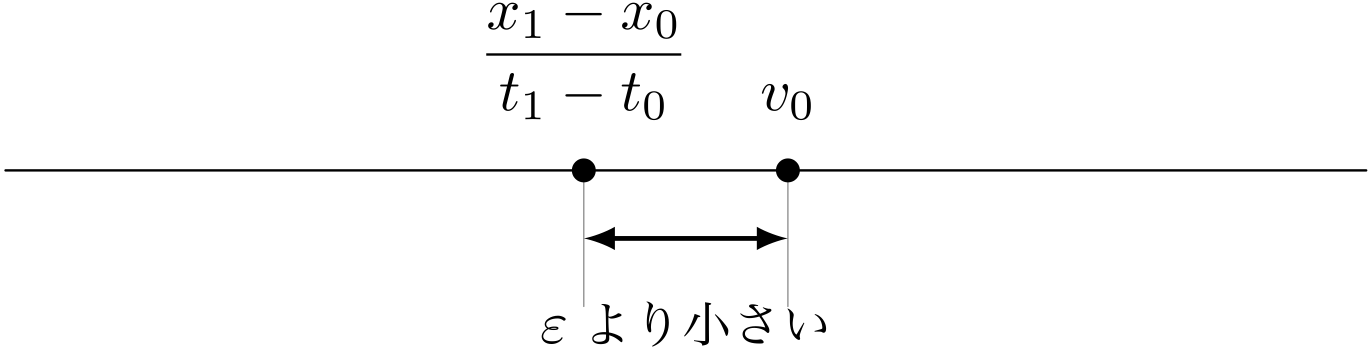
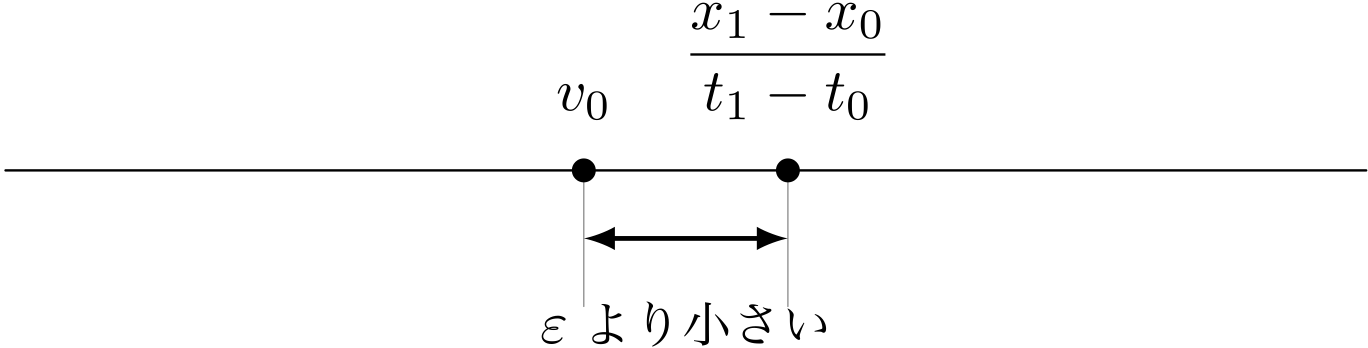
ユーリ「ははーん。 こーゆー状況だから、 $\EPSLN$ を小さくすればするほど、 《瞬間の速度》は《平均の速度》に近くなるぞっと……それからそれから？」

僕「うん、でも、これだけじゃ《瞬間の速度》を定義するのに足りない。もう一つ見積もらなきゃいけないものがある」

ユーリ「もう一つ？」

僕「二つの時刻 $t_0$ と $t_1$ の差だね。 《平均の速度》というときには、二つの異なる時刻が必要だった。 $\EPSLN$ とは別に、 $\DLT$（デルタ）という正の数を使って、こんな不等式を考えることになる」

ユーリ「でるた」

僕「この不等式はユーリも読めるよね」

ユーリ「さっきと同じ考え方でしょ？　 $t_0$ と $t_1$ は、そんなに離れてない。 $\DLT$ 以上は離れてない」

僕「そうそう。それでいいよ。あとはこの二つの不等式をうまく組み合わせれば、 《瞬間の速度》と呼ぶのにふさわしい $v_0$ を定義できるんだ」

直観と数式

ユーリ「ねーお兄ちゃん。でも《瞬間の速度》って《瞬間》の速度だよね？　 $t_0$ と $t_1$ みたいに時刻が二つあったら《瞬間》にならないよ？」

僕「その通りだね。だから時刻 $t_0$ における《瞬間の速度》$v_0$ という言い方になる。 $t_0$ 一つしか出てこない」

ユーリ「うっわー、またわかんなくなった。時刻が $t_0$ ひとつしかないなら点 $P$ は動かないじゃん？　それなのに速度が定義できるの？」

僕「いやいや、ユーリ。話が戻ってるよ。考え方を変える必要がある。 《瞬間の速度》を定義するときに、瞬間で点 $P$ が動くかどうかという直観的な話にしちゃだめ。 そういう直観に頼って定義するんじゃないんだ。数式に頼って定義するんだ」

ユーリ「直観じゃなくて数式……でもさっき、『《瞬間の速度》$v_0$ はこんな不等式を満たしてほしい』って言ってたじゃん！　あれは直観じゃないの？」

僕「おおお……ユーリは鋭いにゃあ」

ユーリ「猫語、真似するなー！」

僕「《瞬間の速度》$v_0$ はこんな不等式を満たしてほしい……というのは直観というか何というか、うーん、そうだなあ、どう話せばいいかなあ」

ユーリ「どー聞けばいいかにゃあ？」

僕「僕たちはいま《瞬間の速度》を定義したいんだけど、 何もないところから直観を使って《瞬間の速度》を定義したいんじゃない。 《平均の速度》を定義している数式を使って《瞬間の速度》を定義したいんだよ。 そしてその数式を調べて『ああ、確かにその定義は《瞬間の速度》と呼ぶのににふさわしいなあ』と直観的にも納得したいんだ。 こんな不等式を満たしてほしいというのは、最後のその納得を先取りした気持ちなんだよ。 直観を数式に落とし込んだというか……」

ユーリ「うみゅう……その数式へのこだわり、嫌いじゃないけど？」

僕「直観をもとに議論するのは難しい。だって、人によって意味が違うかもしれないから。 《その瞬間において》や《その一瞬で》が何を意味するかは直観だけを頼りにしてたらもやもやする。 でもいったん数式に落とし込んで表現し、それをもとに議論すれば安心。 何を主張しているかが明確になるから、議論の行き違いも防げる。 数式を使って定義すれば、その数式から導けることは確信をもって成り立つといえる」

ユーリ「オッケー！　話を先に進めてくれたまえ！」

僕「ここまで来たら《瞬間の速度》の定義を読めると思うな」