![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
ユーリ:僕のいとこの中学生。 僕のことを《お兄ちゃん》と呼ぶ。 論理的な話は好きだが飽きっぽい。
ユーリ「お兄ちゃん、ビブンって何?」
僕「え?」
いとこのユーリは中学生、 しょっちゅう僕の部屋にいりびたっている。 今日はいきなり質問だ。
ユーリ「だから、ビブンって何?」
僕「微分? ねえユーリ、これと同じ会話したことない?」
ユーリ「タイムループ」
僕「微分だったら、何回か説明したことあるよね」
ユーリ「お兄ちゃん、いつも《わからなくなったら、何度でも聞き直していいんだよ、かわいいユーリ》っていうじゃん。だから聞いてるの」
僕「ちょっと質問いいかな。また、例の友達と数学クイズでバトってるんだね?」
ユーリには数学好きの友達がいて、いっしょに問題を解き合ったりしているらしい。
ユーリ「ふっ……勘がいいお兄ちゃんはキライだよ。あのね、微分のこと《瞬間の変化率》だって教えてくれたじゃん?」
僕「強いて一言でいうならそうなるよ。点が動く速度を例にして計算したよね。《位置のグラフ》から《速度のグラフ》を作ったりして」
ユーリ「でもね、ユーリわかんなくなっちゃったの! 問題はこれ!」
ユーリのグラフ
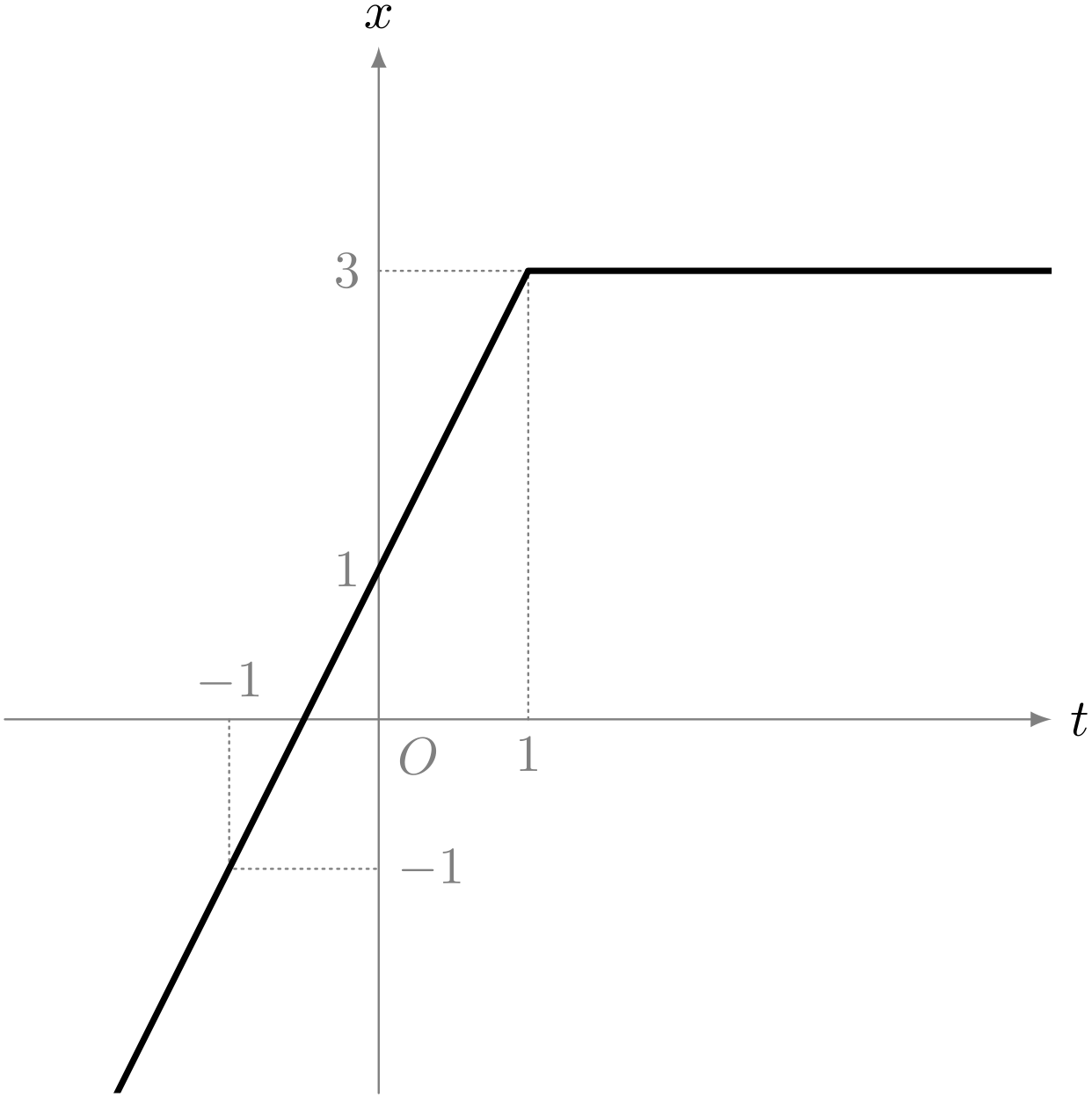
僕「なるほど?」
ユーリ「ね?」
僕「いやいや、『ね?』じゃないよ。このユーリのグラフが何なのか、説明してくれなきゃわからないよ」
ユーリ「だからさー、ここの折れてるところの瞬間はどーするかって問題」
僕「いやいや、『だからさー』じゃないよ。このユーリのグラフはどんなもののどんな状況を表していて、何が問題になっていて、 ユーリが疑問に思っていることは何かを順序立てて説明してくれなくちゃ。そうしないと、さっぱりわからない」
ユーリ「うー、めんどい」
僕「よろしく、ユーリ先生」
ユーリ「こんなふうにして、僕たちの旅が始まった。 このときには、未来にどんな困難が待ち受けているのか二人とも想像できなかったのだ……」
僕「ナレーションはいいから」
ユーリ「あのね、時刻 $t$ のとき位置 $x$ に点 $P$ があるの」

僕「なるほど。数直線上に点 $P$ があると」
ユーリ「そーそー。さっきのユーリのグラフは点 $P$ の動きを表してるつもり」
僕「時刻 $t$ と位置 $x$ の関係を表した《位置のグラフ》ということだね」
ユーリ「でね、ここの折れてるところがわかんないの」
折れてるところ
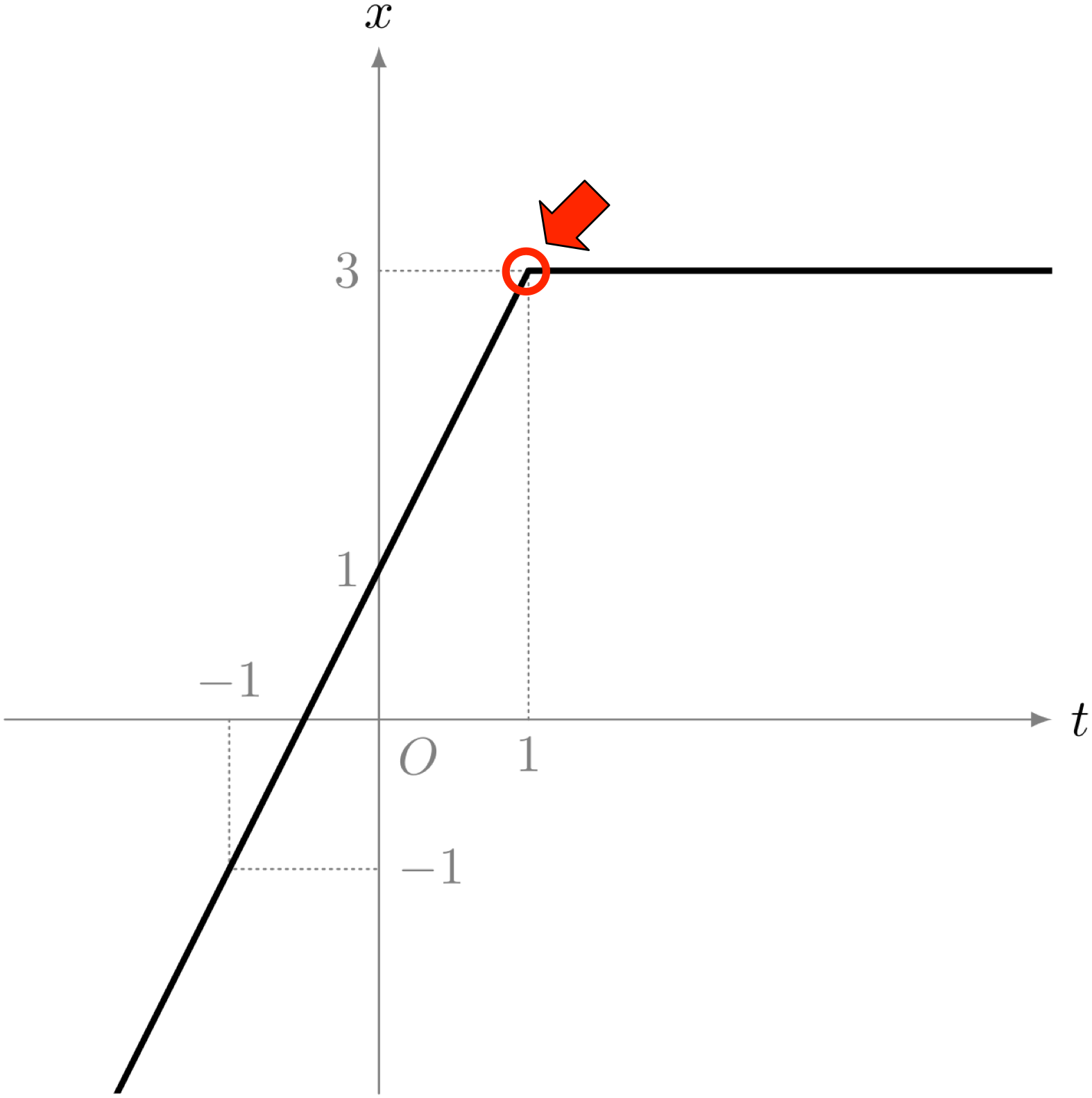
僕「いきなり話を飛ばさないでほしいなあ、ユーリ。 そもそも、点 $P$ がどんなふうに動いているか、ユーリはわかってるの?」
ユーリ「わかってるよん。点 $P$ はずっと同じ速度で動いているんでしょ。時刻が $1$ になるまでは」
僕「そうだね、この点は等速直線運動をしてる」
ユーリ「点 $P$ は時刻 $1$ まで等速直線運動をしてきて、時刻 $1$ で急ブレーキ掛けて止まったの」
僕「うんうん、その通りだね。ところでユーリは、どうして《止まった》ってわかったんだろう」
ユーリ「来たな《先生トーク》」
僕「茶化すなよ」
ユーリ「だってね、時刻 $1$ からあとはずっと位置が変わらないもん。位置が変わらないってゆーのは《止まった》ってことじゃん」
僕「そうだね。じゃ、どうして《急ブレーキ掛けた》って言える?」
ユーリ「グラフの通りでしょ?」
僕「そうなんだけど、グラフのどこをどう見たら《急ブレーキ掛けた》って言えるか、って聞いてるんだけど」
ユーリ「うーん……わかるんだけど、なんて言えばいいかわかんない」
僕「思った通り言ってみたら」
ユーリ「あのね、かくんってグラフ折れてるから。折れてるから《急ブレーキ》だなってわかる」
僕「そうだね! もしも、急ブレーキ掛けるんじゃなくて、スピードをゆっくり落として止まったのなら、こんなグラフになるはずだからね」
スピードをゆっくり落として止まった場合のグラフ
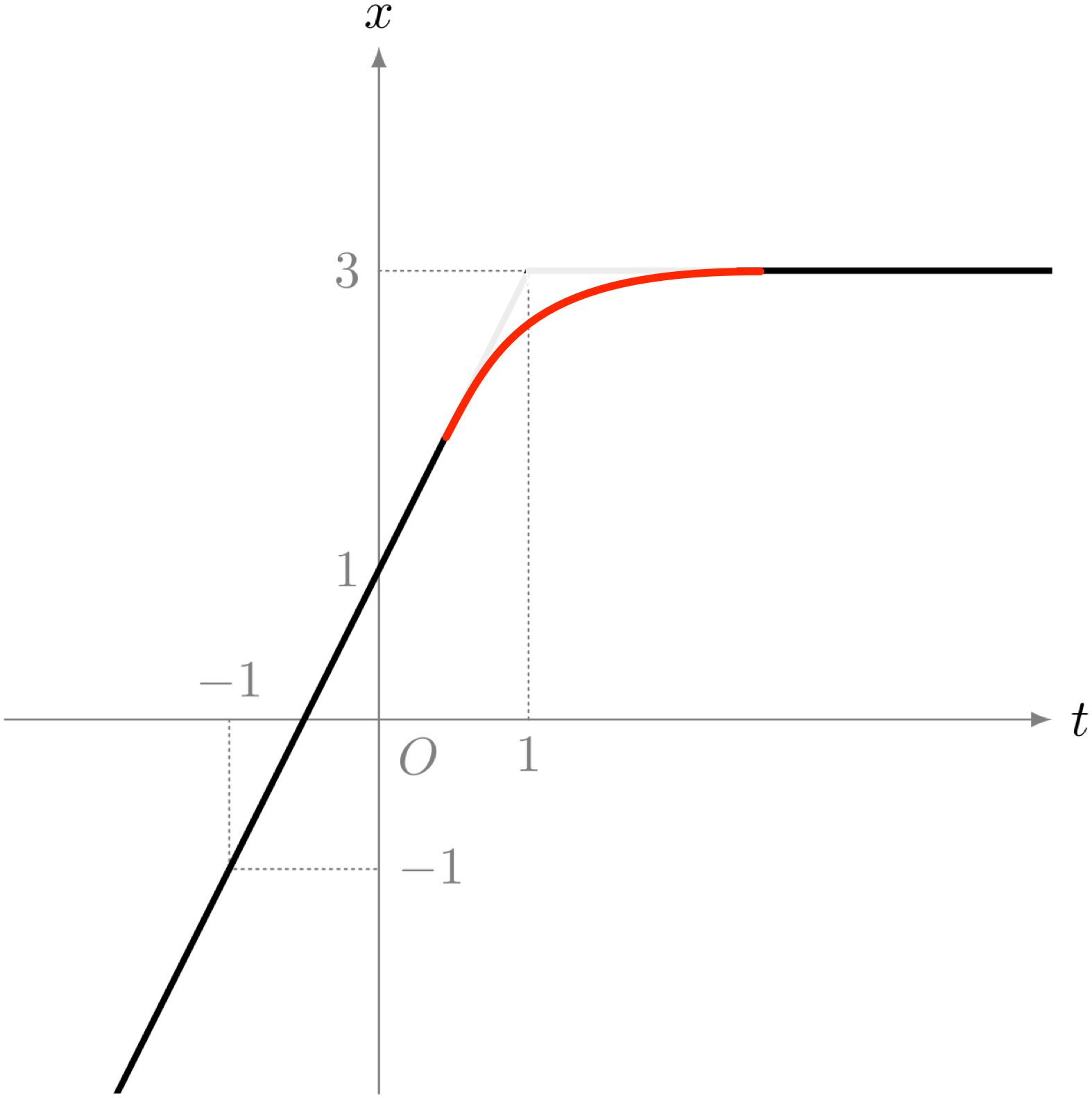
ユーリ「それっ! それそれ!」
僕「びっくりした。何が?」
ユーリ「ユーリがお兄ちゃんに聞きたいことがそれ! いまお兄ちゃんが描いたグラフだと、点 $P$ が止まるまで時間が掛かってるよね?」
僕「そうなるね。だんだん遅くなって止まる感じだ」
ユーリ「でも、ユーリのグラフだと《時刻 $1$ までの速度は $0$ ではない》けど《時刻 $1$ からの速度は $0$ である》よね?」
僕「うん、それでまちがいないよ」
ユーリ「だったらね、その境目、時刻 $1$ の《瞬間の速度》はどーなるの?」
ユーリの疑問
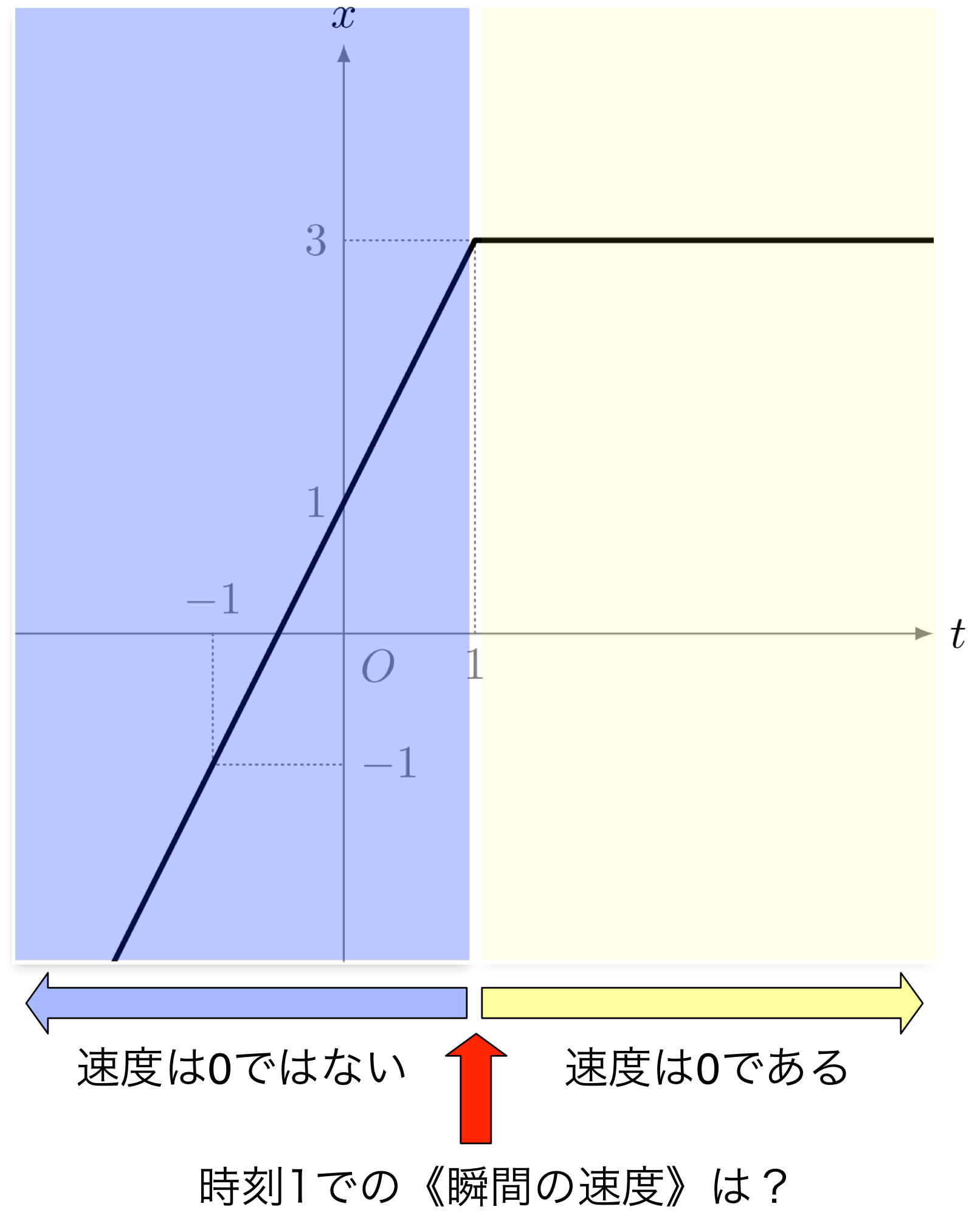
僕「なるほど。ユーリの疑問はすばらしいなあ」
ユーリ「ねーねー、時刻 $1$ の《瞬間の速度》はどーなるの?」
僕「ユーリはどう思う?」
ユーリ「ユーリはね、 時刻 $1$ のぎりぎり直前までは速度 $0$ じゃなくて、 時刻 $1$ から速度 $0$ になるんだと思ってる。 だから『時刻 $1$ の《瞬間の速度》は $0$ である』と思ったんだけど……でも」
僕「でも?」
ユーリ「でも、あんま自信ない」
僕「いろいろ考えたんだろ?」
ユーリ「うん、あのね、お兄ちゃんから微分の計算って教えてもらったじゃん。 ほらほら、 $t^2$ を微分すると $2t$ になるってゆーの(『数学ガールの秘密ノート/微分を追いかけて』参照)」
僕「そうだったね」
ユーリ「それを使えばわかる! ……って思ったけど、でも、ユーリのグラフだと、 折れてるところはちょうど式の境目になってる! それでわかんなくなった。ビブンって何? 瞬間って何? 動いた点が止まるだけなのに、何でこんなにごちゃごちゃするの?」
僕「ねえ、ユーリはすごいよ。よくそれだけしっかり考えられるなあ。 時刻 $1$ の《瞬間の速度》を考えるときは『めんどくさいからいいや』って言わないんだね」
ユーリ「だって、気になるし。 時刻 $1$ より前の速度が $0$ じゃないのは確実でしょ。だって動いているから。 それから時刻 $1$ より後の速度が $0$ なのも確実。だって止まっているもん。 でも、時刻がちょうど $1$ のとき……その瞬間だけ速度がわかんない。 そこだけわかんないって気持ち悪い……そんで、答えは?」
ユーリは目を輝かせて僕にせまる。
僕「答えは、決まらないになるね」
ユーリ「決まらない! そんなのアリなの?」
僕「うん。あくまで点 $P$ がユーリのグラフの通りに動いた場合だよ。そのときには時刻 $1$ の《瞬間の速度》は決まらないんだ。 だって、点 $P$ の位置 $x$ を時刻 $t$ で微分しようとしても、時刻 $1$ のところでは微分できないから」
ユーリ「微分できない! 超ショック。そんな答え、あるんだ? うわー、納得できなーい!」
僕「微分の定義から論理的に説明できるよ」
ユーリ「難しい話で煙に巻かれるのか……」
僕「そんなことないよ。ユーリにわかるように説明するから大丈夫」
ユーリ「よろしく、お兄ちゃん先生」
僕「時刻 $1$ のとき、点 $P$ の《瞬間の速度》を知りたいんだよね。ユーリは」
ユーリ「そーだよん」
僕「それを正確に知るためには《瞬間の速度》という言葉の定義をきちんとする必要があるよね」
ユーリ「てーぎ」
僕「そう。《瞬間の速度》という言葉をどんな意味で使っているかをはっきりさせなかったら、正確な話はできないから」
ユーリ「ふむふむ。それが微分なんでしょ?」
僕「そうなんだけど、先を急がずにじっくり行こう。《瞬間の速度》を定義するために、まずは《平均の速度》を定義しよう」
ユーリ「へーきんのそくど」
《平均の速度》の定義
直線上にある点 $P$ について、こんなことがわかっていたとしよう。
このとき、時刻 $t_0$ から $t_1$ までの《平均の速度》は、 $$ \dfrac{x_1 - x_0}{t_1 - t_0} $$ であると定義する。ただし、 $t_0 \neq t_1$ と仮定する。
僕「これはどう? 難しい?」
ユーリ「んー、数式を使ってややこしく説明してるけど、これって要するにあれでしょ? 《動いた距離》を《掛かった時間》で割るってことでしょ? だったらわかるよん」
僕「そうだね。おおよそは、それで合ってる。 《動いた距離》というと向きのことを考えていないみたいに聞こえるから、 《位置の変化》とか変位といった方が正確だね」
ユーリ「むー……」
僕「言葉で説明するのはわかりやすいといえばわかりやすいけど、 さっきの《平均の速度》の定義のように、文字や数式をうまく使った方が誤解は減るんだよ。 だって、 $$ \dfrac{x_1 - x_0}{t_1 - t_0} $$ という定義で、 $x_1 - x_0$ という部分の値が正になるか負になるかで、向きが考慮されていることがわかるから」
ユーリ「らじゃりました」
僕「もっと大切なこともあるよ。《平均の速度》の定義をもう一度みてごらん」
ユーリ「じー」
《平均の速度》の定義
直線上にある点 $P$ について、こんなことがわかっていたとしよう。
このとき、時刻 $t_0$ から $t_1$ までの《平均の速度》は、 $$ \dfrac{x_1 - x_0}{t_1 - t_0} $$ であると定義する。ただし、 $t_0 \neq t_1$ と仮定する。
僕「この《平均の速度》の定義だと、《平均の速度》を求めるためには二つの時刻における位置さえ得られればいいんだってわかるよね。 つまり、 《時刻 $t_0$ のときの位置 $x_0$》と《時刻 $t_1$ のときの位置 $x_1$》 という二つさえわかれば、《平均の速度》は求められる。 言い換えると、点 $P$ が $t_0$ と $t_1$ 以外の時刻にどんな動きをしているのかは気にしなくていいということ。 気にしなくても $t_0$ から $t_1$ までの《平均の速度》は求められる。 これがすごくいいんだよ。ものごとを考えやすくしてくれる」
ユーリ「ほほー……どゆこと?」
僕「点の動きを考えるとき、僕たちはつい頭の中で点を動かして考えてしまう。 もちろんそれでもいいんだけど、動かしながら考えるのは難しかったり、かえって誤解する場合もある。 だから、必要に応じて止めて考えることができるのはとても大事なんだよ」
ユーリ「それ、おかしなこと言ってない? 点の動きを考えるんだけど、止めて考える……?」
僕「矛盾していることを言いたいわけじゃないよ。 僕たちは点の動きをとらえたい。そのときに大事なのは時刻と位置の関係だよね。 《点 $P$ は、時刻 $t_0$ のとき位置 $x_0$ にある》という言い方は、時刻 $t_0$ という値に止めて考えているわけだよ。 だって、《時刻 $t_0$ のとき》といったら、点の位置は少しも動かないから。 僕たちは点がふらふら動き出す心配はしなくてもいい。 《時刻 $t_0$ のとき》と時刻を固定している限り、点の位置は $x_0$ から動かない」
ユーリ「むむ? むむむ? ちょっと待ってよ、お兄ちゃん。 時刻を固定して考えたら点は動かないってゆーのはわかるんだけど、 そんなこといったら《瞬間の速度》なんてありえない! だって、瞬間は瞬間だよ? 時刻が変化しちゃったら瞬間じゃない。 時刻が変化しなかったら、点は動かない。だったら《瞬間の速度》なんて考えてもイミないじゃん!!」
ユーリは腕組みをして僕をにらむ。
僕「ユーリは賢いなあ! 確かに《瞬間の速度》という言葉から考えちゃうと、《瞬間の速度》なんてありえないように聞こえてしまう。 時刻が変化しないのに速度なんて考えられないと思っちゃう」
ユーリ「……」
僕「ねえユーリ、僕たちはだから数式を使うんだよ。 言葉が持つ印象だけで考えを進めようとすると、かえって難しいんだ」
ユーリ「でも……」
僕「《瞬間の速度》について考える前に、もう少し《平均の速度》について確かめておこうよ。 だって、僕たちはこれから《平均の速度》をもとにして《瞬間の速度》を考えることになるんだから」
ユーリ「オッケー」
僕「ところで、さっきの《平均の速度》の定義には一つ仮定があったけど、ユーリは見逃してないよね?」
ユーリ「もちろん。 $t_0 \neq t_1$ のことでしょ?」
僕「そうだね。これはどういう意味だと思う?」
ユーリ「時刻 $t_0$ と時刻 $t_1$ は等しくない」
僕「正解。つまりこの《平均の速度》の定義では、異なる二つの時刻が必要だということだね」
ユーリ「あ、そーゆーことか。ユーリは、 $$ \dfrac{x_1 - x_0}{t_1 - t_0} $$ で分母が $0$ にならないよーにするためかと思った」
僕「うん。だから $t_0 \neq t_1$ だとこの分数の値は必ず決まることがわかる」
ユーリ「だよね」
僕「じゃ、具体的に《平均の速度》を計算してみよう。たとえば、こんな問題」
問題1(平均の速度)
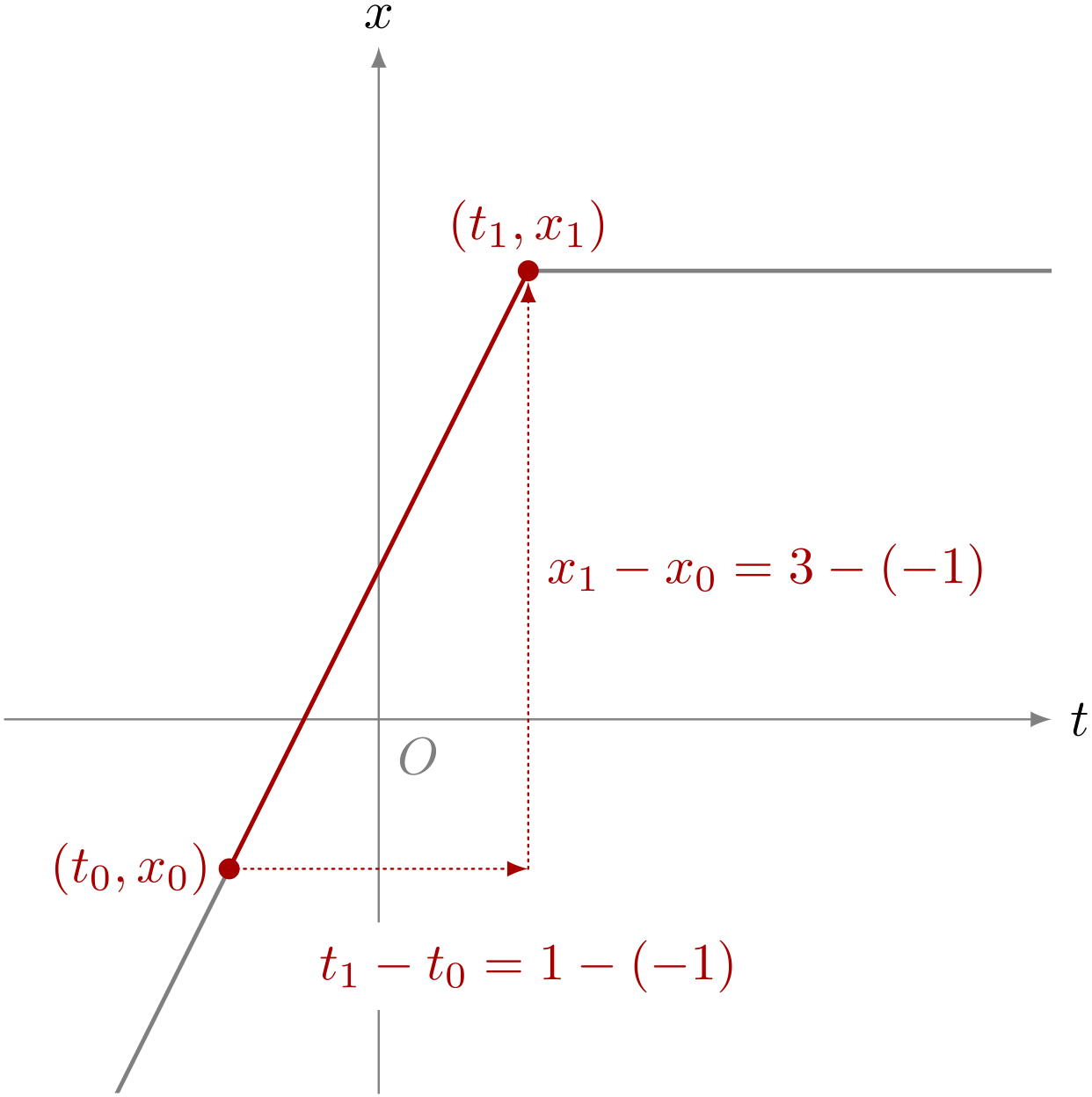
ユーリのグラフで、 時刻 $-1$ から $1$ までの《平均の速度》は?

ユーリ「こんなの簡単だよー。そのまま計算すればいーんでしょ?」
僕「そうだね。定義通りに計算すればいいよ。 $t_0 = -1$ で $t_1 = 1$ として考えるわけだから……」
ユーリ「はいはい、計算するよー…… $$ \begin{align*} \dfrac{x_1 - x_0}{t_1 - t_0} &= \dfrac{3 - (-1)}{1 - (-1)} && \REMTEXT{$t_0 = -1$のとき$x_0 = -1$で、$t_1 = 1$のとき$x_1 = 3$だから} \\ &= \dfrac{3 + 1}{1 + 1} \\ &= \dfrac{4}{2} \\ &= 2 \end{align*} $$ だから、平均の速度は $2$ だね!」
僕「はい、正解。 $3 - (-1)$ が $x_1 - x_0$ に相当して、 $1 - (-1)$ が $t_1 - t_0$ にあたってる」
解答1(平均の速度)
時刻 $-1$ から $1$ までの《平均の速度》は $2$ である。
ユーリ「簡単、簡単」
僕「じゃあ、この問題は?」
問題2(平均の速度)
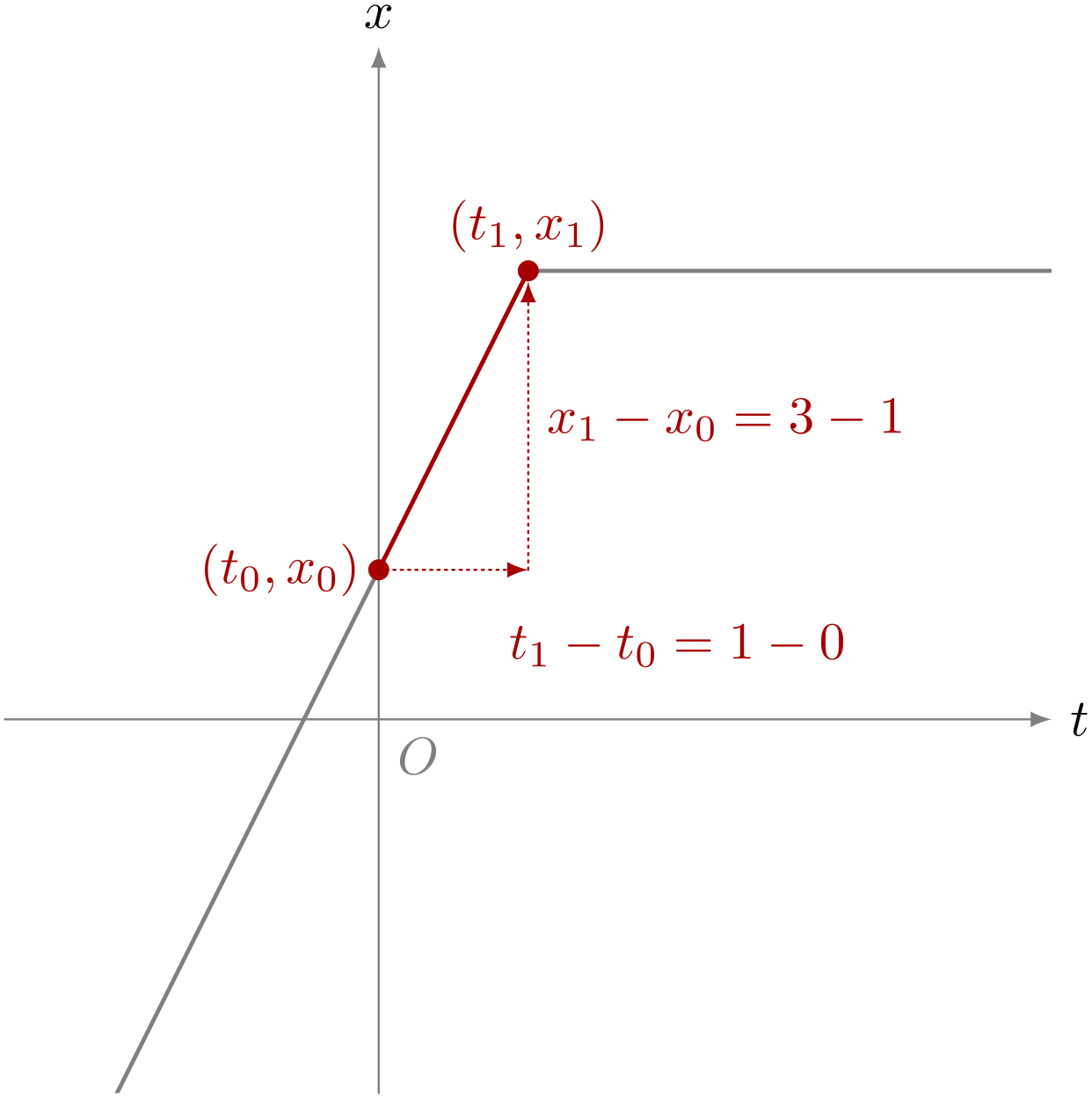
ユーリのグラフで、時刻 $0$ から $1$ までの《平均の速度》は?

ユーリ「これもカンタン! 定義通りに計算すれば…… $$ \begin{align*} \dfrac{x_1 - x_0}{t_1 - t_0} &= \dfrac{3 - 1}{1 - 0} && \REMTEXT{$t_0 = 0$のとき$x_0 = 1$で、$t_1 = 1$のとき$x_1 = 3$だから} \\ &= \dfrac{2}{1} \\ &= 2 \end{align*} $$ だから、平均の速度は $2$ ……って、計算しなくてもよかった!」
僕「どうして?」
ユーリ「だって、直線じゃん」
僕「そうだね。グラフが直線だったら、その中のどの二点を選んでも《平均の速度》はいつも等しい。 それは、 $$ \dfrac{x_1 - x_0}{t_1 - t_0} $$ という《平均の速度》を計算すると、二点 $(t_0,x_0)$ と $(t_1,x_1)$ を結ぶ直線の傾きに等しくなるから」
ユーリ「あー、直線の傾き。それそれ」
僕「直線上の二点を考えるなら、 $t_1 - t_0$ が大きくなったときには、ちょうどそれに比例して $x_1 - x_0$ も大きくなるからね」
ユーリ「ふんふん」
解答2(平均の速度)
時刻 $0$ から $1$ までの《平均の速度》は $2$ である。
僕「じゃあ、こんな問題はどうかな」
問題3(平均の速度)
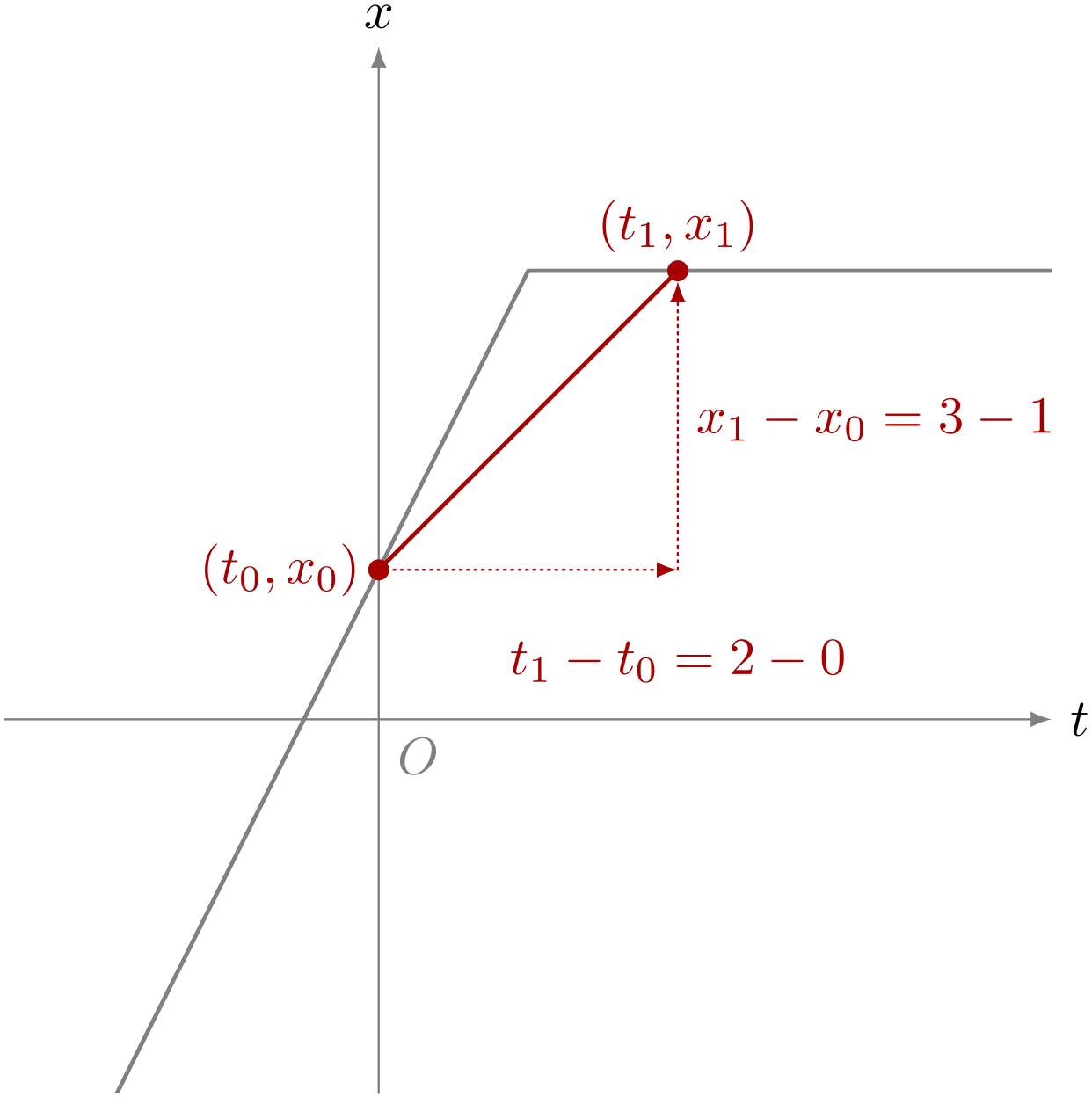
ユーリのグラフで、時刻 $0$ から $2$ までの《平均の速度》は?

ユーリ「だからー、途中の折れ線が気になるんだって!」
僕「だからー、気にしなくていいんだって! いまは《平均の速度》を考えているんだから、 $t = 0$ のときと、 $t = 2$ のときだけを見ればいいんだよ」
ユーリ「あっ、そっか! だったら…… $$ \begin{align*} \dfrac{x_1 - x_0}{t_1 - t_0} &= \dfrac{3 - 1}{2 - 0} && \REMTEXT{$t_0 = 0$のとき$x_0 = 1$で、$t_1 = 2$のとき$x_1 = 3$だから} \\ &= \dfrac{2}{2} \\ &= 1 \end{align*} $$ だから、平均の速度は $1$ になる?」
解答3(平均の速度)
時刻 $0$ から $2$ までの《平均の速度》は $1$ である。
僕「そうだね、それでいいよ。じゃ、これは?」
問題4(平均の速度)
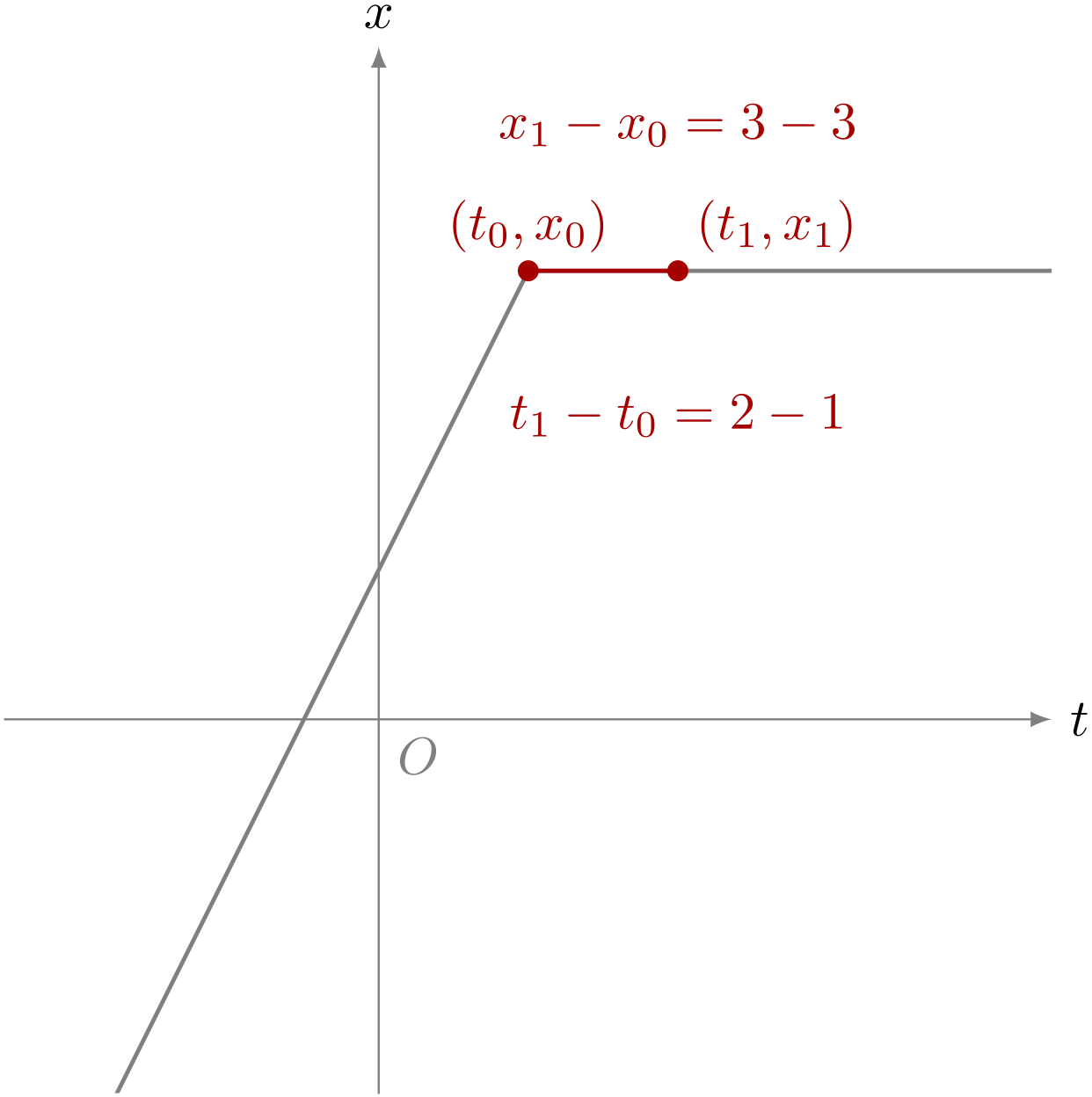
ユーリのグラフで、時刻 $1$ から $2$ までの《平均の速度》は?

ユーリ「止まっているから $0$ でしょ?」
僕「そうなんだけど《平均の速度》の定義からするとどうなる?」
ユーリ「えーと…… $$ \begin{align*} \dfrac{x_1 - x_0}{t_1 - t_0} &= \dfrac{3 - 3}{2 - 1} && \REMTEXT{$t_0 = 1$のとき$x_0 = 3$で、$t_1 = 2$のとき$x_1 = 3$だから} \\ &= \dfrac{0}{1} \\ &= 0 \end{align*} $$ ね? 平均の速度は $0$ でしょ?」
僕「そうだね。分子の $x_1 - x_0$ が $0$ になるから《平均の速度》は $0$ になる」
解答4(平均の速度)
時刻 $1$ から $2$ までの《平均の速度》は $0$ である。
ユーリ「ねー、飽きてきたよー。早く《瞬間の速度》の話をしてよー」
僕「どうせだから、《瞬間の速度》をどう定義すればいいか、いっしょに考えよう、ユーリ」
ユーリ「あいよ」
僕「僕たちは《平均の速度》を知ってる」
ユーリ「うん」
僕「《位置のグラフ》の中で $(t_0,x_0)$ と $(t_1,x_1)$ の二点を決めれば《平均の速度》が決まる。 《平均の速度》は、こんな直線の傾きの大きさを表している」
《平均の速度》と直線の傾き
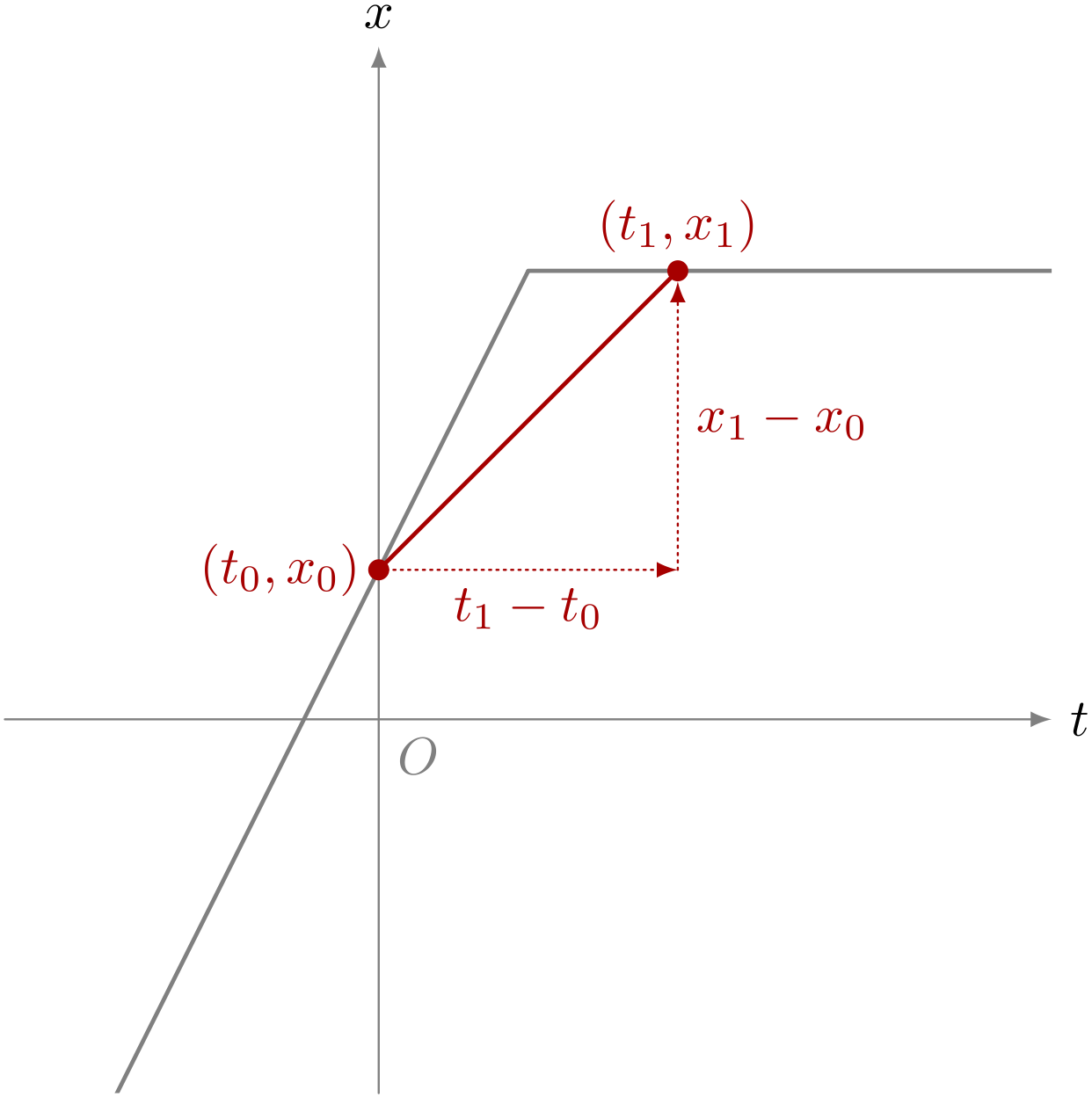
ユーリ「うん、《平均の速度》はわかる」
僕「僕たちは《平均の速度》のとき、二つの時刻を使って計算したよね。 だからたとえば、
時刻 $0$ から $2$ までの《平均の速度》は $1$ に等しい
のように、二つの時刻を使って表現した」
ユーリ「……」
僕「でも《瞬間の速度》のときは、一つの時刻を使って表現したい。
時刻 $t_0$ の《瞬間の速度》は $v_0$ に等しい
のようにね」
ユーリ「わかる……けど、時刻 $t_0 = t_1$ にしちゃダメじゃん! 仮定に反するしゼロ割りになるから、《平均の速度》が使えなくなる!」
僕「$t_0=t_1$ なんてことはしないよ」
ユーリ「なんだかドキドキしてきた」
僕「時刻 $t_0$ と $t_1$ が近いときには、《平均の速度》は $v_0$ に近くなってほしいよね」
ユーリ「$v_0$ ってなんだっけ」
僕「$v_0$ というのは、時刻 $t_0$ での《瞬間の速度》のことだよ。まだ定義していないけど、 もしも《瞬間の速度》が $v_0$ だとしたら、それは《平均の速度》に近くなってほしい」
ユーリ「それって、 $t_0$ と $t_1$ が近かったら、時刻 $t_0$ から $t_1$ までの《平均の速度》は $v_0$ に近くなってほしい……ってこと?」
僕「そういうこと。近いとか、近くないとかいう言い方だとモヤモヤするから、もっと正確に言ったほうが気持ちいい」
ユーリ「うん、それ、いまいおうと思った」
僕「だから、どのくらい近いかを文字で表すことにしよう。《平均の速度》は $v_0$ に $\EPSLN$(イプシロン)以上は離れていないとする」
ユーリ「いぷしろん? イプシロンって何?」
僕「$\EPSLN$ は数だよ。 $0$ より大きな数。 《平均の速度》と《瞬間の速度》は $\EPSLN$ 以上は離れていないよということを表すための数としていま導入した」
ユーリ「??」
僕「不等式で表せばはっきりするよ。僕たちはいま、 $$ v_0 - \EPSLN < \dfrac{x_1 - x_0}{t_1 - t_0} < v_0 + \EPSLN $$ という不等式が成り立ってほしい、と思うところまで来たんだ。この不等式に注目だよ」
ユーリ「ほら来た! やっぱり数式でてきたじゃんかー!」
僕「でも、難しくないよ。ただの不等式だよ。出てきた文字もぜんぶわかるよ。 だから、ユーリにも読めるはず」
ユーリ「読める?……うーん、真ん中のこれは《平均の速度》になってるケド」
$$ \dfrac{x_1 - x_0}{t_1 - t_0} $$僕「そうだね! そして $v_0 - \EPSLN$ は《瞬間の速度》よりもちょっと小さい数になる」
$$ v_0 - \EPSLN $$ユーリ「$v_0$ から $\EPSLN$ を引いてるからちょっと小さいってこと?」
僕「そうだね。そして $v_0 + \EPSLN$ は《瞬間の速度》よりもちょっと大きい数」
ユーリ「……わかった!! この不等式って、もしかしてはさみうちのつもり?」
$$ v_0 - \EPSLN < \dfrac{x_1 - x_0}{t_1 - t_0} < v_0 + \EPSLN $$僕「おっと! どうして急に話が進むんだ?」
ユーリ「面積の計算するとき、似たようなことやったもん。小さな面積 $L_n$ と大きな面積 $M_n$ で、ほんとの面積 $S$ をはさむの!」
僕「それは、区分求積法の話だね。発想は似てるよ(『数学ガールの秘密ノート/積分を見つめて』参照)」
ユーリ「うんうん、早く先を話して!」
$$ v_0 - \EPSLN < \dfrac{x_1 - x_0}{t_1 - t_0} < v_0 + \EPSLN $$僕「この不等式は《平均の速度》が《瞬間の速度》に近いことを表している。 どのくらい近いかというと $\EPSLN$ 以上は離れないくらい近いということ」
ユーリ「……」
僕「いま僕たちは《瞬間の速度》というものを定義したい。定義するときに《平均の速度》を利用する。 《瞬間の速度》というものがあったとして《平均の速度》がどれだけそれに近いかを $\EPSLN$ という正の数で見積もったともいえる」
ユーリ「うん……」
僕「でも、これだけじゃ足りない。もう一つ見積もらなきゃいけないものがある」
ユーリ「もう一つ?」
僕「うん。それは二つの時刻 $t_0$ と $t_1$ の差だね。さっきと同じように不等式を使う。さっきと違う数 $\DLT$(デルタ)を使う」
$$ -\DLT < t_1 - t_0 < \DLT $$ユーリ「でるた」
僕「この不等式はユーリも読めるよね」
ユーリ「うん……うん。 $t_0$ と $t_1$ は、そんなに離れてない。 $\DLT$ 以上は離れてない」
僕「そうそう。それでいいよ。あとはこの二つの不等式をうまく組み合わせれば、 時刻 $t_0$ における《瞬間の速度》と呼ぶのにふさわしい $v_0$ を定義できるんだ」
ユーリ「それが《瞬間の速度》の定義?」
僕「そういうことだね」
ユーリ「二つの不等式をうまく組み合わせる……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第221回終わり)
(2018年4月20日)