![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
テトラ「……以前、 $\EPSLN{}N$ 論法や $\EPSLN{}\delta$ 論法を学んだときは、 極限と収束のことを《論理》の話だと強く思いました。 それはそうなんですが、今日あたしは極限というのは《大きさを評価する不等式》の話なんだと思ったんです」
僕「うんうん、おもしろいなあ。もちろんその両方が出てくるけどね」
テトラ「はい。先輩の証明(第219回参照)を読んでいて、 《論理に注意しながら、不等式で大きさを評価している》 と感じたんです。そして気がつくと、証明の中には《無限》や《無数》という言葉は出てきません。 《有限》は出てきました。十分大きな $M$ を使って $A_1 + A_2 + \cdots + A_{N_A}$ をやっつけるところです。 でもそこでも、《無限》を使ってやっつけたわけじゃありません。 《有限》の $M$ でやっつけました。 そういうことを考えていたんです」
僕「確かにそうだね。《無限》は表には出てこないけど、 《十分大きな $M$ を選ぶことができる保証》に隠れているといえそうだね」
テトラ「なるほどです! ……あたしがおもしろいと思ったのは、
《無限》をきちんと扱うのに、《無限》という言葉が出てこない
という点でした」
僕「それは自然なことじゃないかなあ」
テトラ「何がですか?」
僕「うん、だからね、
《無限》をきちんと扱うのに、《無限》という言葉が出てきてはいけない
と思うんだ。よくわかっている別のことで言い換えるからこそ、きちんと扱えるんだから」
テトラ「あっ……深いですね」
僕「それにしても、平均の極限値はおもったより手強かったなあ」
テトラ「そうですね。でもあたし、 $\EPSLN N$ 論法のことちょっぴりわかったように思います。 《評価する》という感覚のことです」
僕「それはすごい! じゃ、 $\EPSLN\DLT$ 論法もやってみようか。 テトラちゃん、以前いっしょに読んだのを覚えているよね」
テトラ「は、はい。 $\EPSLN N$ 論法は数列の極限で、 $\EPSLN\DLT$ 論法は関数の極限で出てきました」
僕「そうそう。 $\EPSLN N$ 論法と、 $\EPSLN\DLT$ 論法を比べてみよう」
数列の極限(極限値 $A$ に収束する数列)
数列 $\LL a_n \RR$ を考える。また、 $A$ を実数とする。
どんな正の数 $\EPSLN$ に対しても、次の条件を満たす正の整数 $N$ が存在するとしよう。
条件: $n > N$ であるすべての整数 $n$ について $\ABS{a_n - A} < \EPSLN$
このとき、 $$ n \to \infty \quad\REMTEXT{で}\quad a_n \to A $$ と書き、数列の一般項 $a_n$ は極限値 $A$ に収束するという。
関数の極限(極限値 $A$ に収束する関数)
実数全体から実数全体への関数 $f(x)$ を考える。 また、 $A$ を実数とする。
どんな正の数 $\EPSLN$ に対しても、次の条件を満たす正の数 $\DLT$ が存在するとしよう。
条件: $0 < \ABS{x - a} < \DLT$ であるすべての実数 $x$ について $\ABS{f(x) - A} < \EPSLN$
このとき、 $$ x \to a \quad\REMTEXT{で}\quad f(x) \to A $$ と書き、関数 $f(x)$ は $x \to a$ で極限値 $A$ に収束するという。
テトラ「はい……これは先輩に何回か教えていただきました。 文字がいっぱい出てくるので、毎回あせってしまうんですが」
僕「うん、でもわかっているよね。正の数 $\EPSLN$ が与えられて、 $\ABS{f(x) - A} < \EPSLN$ を満たすほど、 $f(x)$ は $A$ という値に近付けるかな……と挑戦を受ける」
テトラ「は、はい。大丈夫です。その $\ABS{f(x) - A} < \EPSLN$ という式は、 《$f(x)$ は $A$ から $\EPSLN$ 以上は離れない》と読めばいいんですよね?」
僕「そうだね。そしてこの関数の極限に出てくる《条件》がとても重要」
条件: $0 < \ABS{x - a} < \DLT$ であるすべての実数 $x$ について $\ABS{f(x) - A} < \EPSLN$

テトラ「はい……実数 $x$ が $a$ の《そば》にいるならば、 $f(x)$ は $A$ の《そば》にいる」
僕「その通り。ただしその《そば》の度合いがちゃんと評価されていることに注意するんだよ」
テトラ「あっ、ここでも《評価》が出てくるんですねっ!」
僕「そうだね。実数 $x$ は $a$ の《そば》にいる……このときの《そば》は $\DLT$ で制限がかかっている。 そのときには絶対に、実数 $f(x)$ は $A$ の《そば》にいる……こちらの《そば》は $\EPSLN$ で制限がかかっている。 というのがこの条件だね」
テトラ「いつもそこでひっかかるんですが、 この条件を満たすような $\DLT$ が存在するというところが大事なんですよね?」
僕「そうそう。どんな正の $\EPSLN$ が与えられたとしても、この条件を満たすような $\DLT$ が存在するといえるかな? ということ。 どんな正の $\EPSLN$ に対してもそのような $\DLT$ が存在するならば、 $x \to a$ のとき $f(x) \to A$ だといえるし、 そんな $\DLT$ が存在するとは限らないならば、 $x \to a$ のとき $f(x) \to A$ だとはいえない。 《関数の極限》は、そういう定義になっているね。何がひっかかるの?」
テトラ「いえ、 $a$ と $A$ と $\DLT$ と $\EPSLN$ が出てきて、 $\EPSLN$ が先に与えられて $\DLT$ が存在するかどうかを調べるんですが、 条件のほうでは $\DLT$ の方が先に出てくるので、そこで頭がごちゃごちゃと……」
僕「ああ、なるほどね。 $y = f(x)$ のグラフを描くともっとすっきりするよ。 $a$ と $\DLT$ は《$x$ の側》で、 $A$ と $\EPSLN$ は《$y$ の側》ってことだね。 二つの軸でそれぞれに大きさ比べをしているんだ」
《関数の極限》の説明図
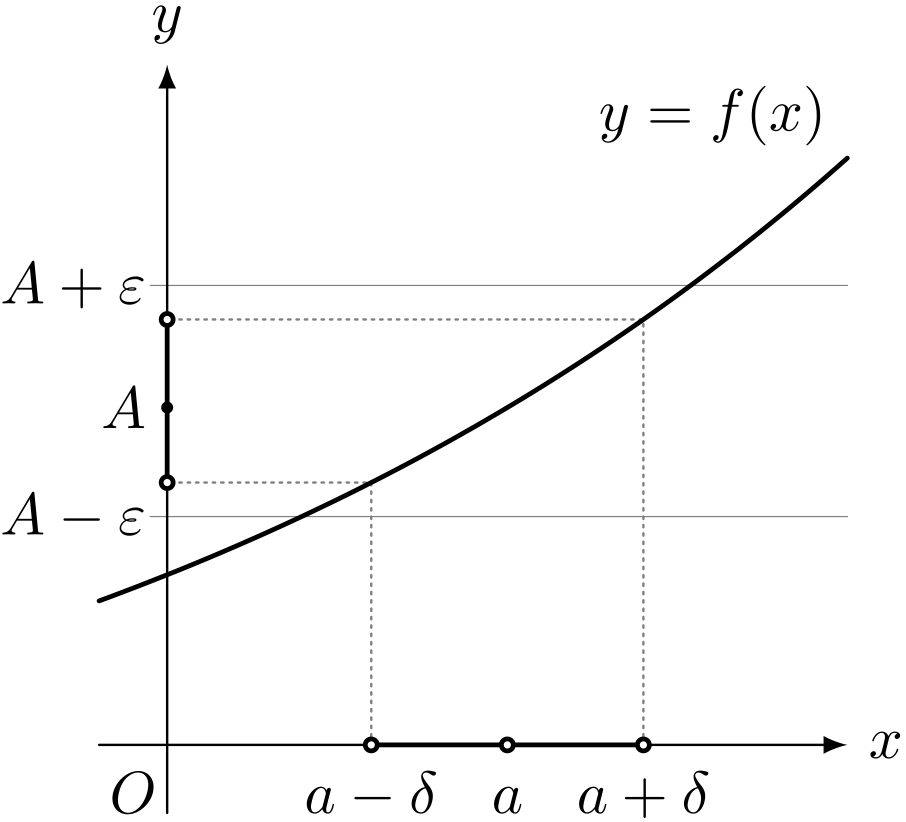
テトラ「ははあ……そういえば、以前もこの図を描いていただいた記憶があります(『数学ガール/ゲーデルの不完全性定理』)」
僕「そうそう。このグラフでいうと、 $0 < \ABS{x - a} < \DLT$ を満たす $x$ に対して、 $f(x)$ がすっぽりと $\ABS{f(x) - A} < \EPSLN$ の範囲に入っているかどうかということだね。 $\EPSLN$ は正ならばいくら小さくてもいい。 $\EPSLN$ をどれだけ $0$ に近付けようとも、その $\EPSLN$ に対して十分小さい $\DLT$ を選べば必ずすっぽり入る。 それが関数の極限」
テトラ「はあ……」
僕「難しい?」
テトラ「い、いえ。難しいといいますか、易しいといいますか……あのですね。 あたしの頭の中をお話しします」
僕「頭の中?」
テトラ「関数の極限というのはイメージとしてはよくわかります。 $x$ が $a$ に限りなく近づくと、 $f(x)$ は $A$ に限りなく近づく」
僕「うん」
テトラ「でも、それだと数学的な議論としてはあいまいなので、 $\EPSLN\DLT$ 論法がある……ですよね?」
僕「そうだね」
テトラ「先ほどの《関数の極限》では $\EPSLN$ と $\DLT$ が出てきて大小関係をあれこれ調べます。 でも、それで《ああ、なるほど》と納得するときには、あたしの頭の中では、 結局その大小関係を《限りなく近づく》というイメージで納得しているように思うんです」
僕「というと?」
テトラ「数式で納得するのではなく、結局イメージで納得しているといいますか……あたし、説明へたですね」
僕「いやいや、すごく微妙な話をしているんだと思うけど」
テトラ「何といいますか……結局のところ、あたしの理解は深まっていないんです。 関数の極限を数式で表しても、あたしの頭の中には《限りなく近づく》という一言しか残ってないといいますか」
僕「わかった。じゃあね、《例示は理解の試金石》でいこう。 《関数の極限》の定義を使って簡単な関数の極限値を求めてみようよ」
テトラ「と、いいますと?」
僕「ちょっとした思いつきなんだけど、 僕たちがふだん《あたりまえ》で済ませることが、 $\EPSLN\DLT$ 論法できちんと証明できることを確認してみるのはどう?」
テトラ「なるほどです……でも、どんな問題でしょうか」
僕「うん、例だからすごく簡単なものにしよう。 たとえば……」
問題(関数の極限)
$x \to 2$ で、 $x^2 \to 4$ になることを $\EPSLN\DLT$ 論法で証明せよ。
テトラ「え……これは、あたりまえじゃないでしょうか。だって $x = 2$ のとき、 $x^2 = 4$ ですから」
僕「そうだね。ここでは $f(x) = x^2$ として考えていて、このとき関数 $f(x)$ は連続だから、代入するだけで極限値が求められる。 それはそうなんだけど、 $\EPSLN\DLT$ 論法で定義された関数の極限を使って本当に $x \to 2$ のとき $x^2 \to 4$ になることが証明できるかな?…… という問題」
テトラ「ははあ……」
僕「僕もこれは考えたことないから、それぞれ考えてみようよ」
テトラ「あっ、ちょっ、ちょっとお待ちください。その前に確認だけさせてください。 証明すべきことはこうですよね?」
問題(テトラちゃんの言い換え)(関数の極限)
どんな正の数 $\EPSLN$ に対しても、次の条件を満たす正の数 $\DLT$ が存在することを証明してください。
条件: $0 < \ABS{x - 2} < \DLT$ であるすべての実数 $x$ について $\ABS{x^2 - 4} < \EPSLN$
僕「その通り! テトラちゃんはちゃんとわかっているね」
テトラ「これは、《定義にかえれ》をやっただけですから……でも、これ、証明できるんでしょうか」
僕「じゃあ、ここからそれぞれ考えよう」
テトラ「はい……」
僕とテトラちゃんは図書室で少し離れた席に移り、それぞれの思考モードに入った。

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年3月16日)