![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
登場人物紹介
僕:数学が好きな高校生。
テトラちゃん:僕の後輩。好奇心旺盛で根気強い《元気少女》。
問題1(極限値の和)
二つの数列 $\LL p_n \RR$ と $\LL q_n \RR$ は、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & p_n \to 0 \\ n \to \infty & \REMTEXT{で} & q_n \to 0 \\ \end{array} $$ とする。
ここで、数列 $\LL r_n \RR$ の一般項を、 $$ r_n = p_n + q_n $$ で定義する。
このとき、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & r_n \to 0 \end{array} $$ を証明せよ。
テトラ「《定義にかえれ》で考えます。 先輩のアドバイス(第218回参照)にしたがって文字を使います!
$p_n \to 0$ ということは、 どんな正の数 $\EPSLN_p$ に対しても、
$n > N_p$ であるすべての整数 $n$ について $\ABS{p_n} < \EPSLN_p$
という正の整数 $N_p$ が存在するということですよね。
それから、 $q_n \to 0$ ということは同じように、 どんな正の数 $\EPSLN_q$ に対しても、
$n > N_q$ であるすべての整数 $n$ について $\ABS{q_n} < \EPSLN_q$
という正の整数 $N_q$ が存在する、ということになります」
僕「そうだね、その通り」
テトラ「先輩、あたし、何をすればいいかは、わかったかも……」
僕「おお」
テトラ「《求めるものは何か》を考えますと、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & r_n \to 0 \end{array} $$ をいうために、 $\EPSLN_r$ に対する、 $r_n$ にとっての $N_r$ を見つければいいんですね?」
僕「そういうことだね。どんな $\EPSLN_r > 0$ が与えられても、ちゃんと $N_r$ を見つければいい」
テトラ「どんな正の数 $\EPSLN_r$ に対しても、 $- \EPSLN_r$ と $\EPSLN_r$ の範囲……《帯》の中に $r_n$ がすっぽり入るように十分大きな $N_r$ を選べばいい?」
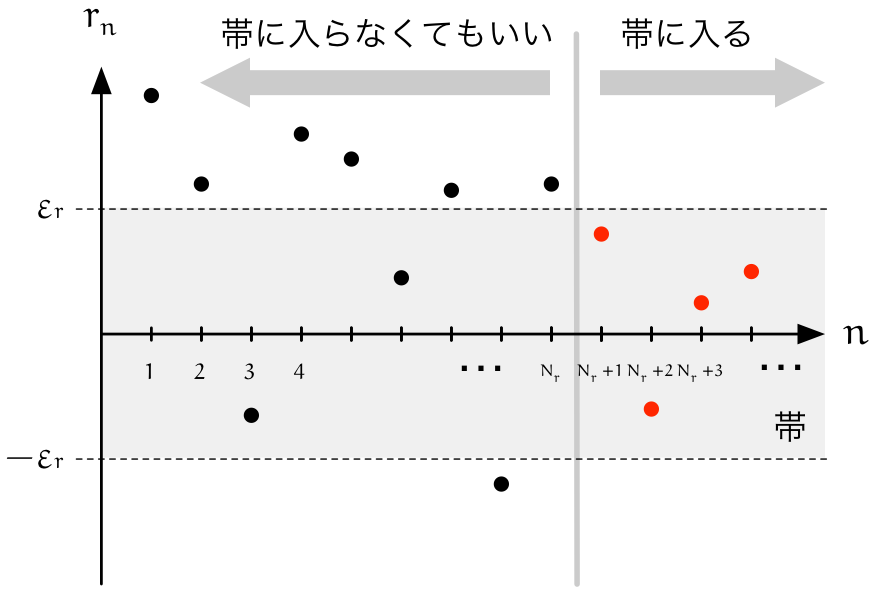
僕「そうだね」
ここでテトラちゃんは長考モードに入る。
テトラ「あのですね、まだはっきりとはわかってないんですが、 やろうとしていることを聞いていただけますか」
僕「もちろん、どうぞ」
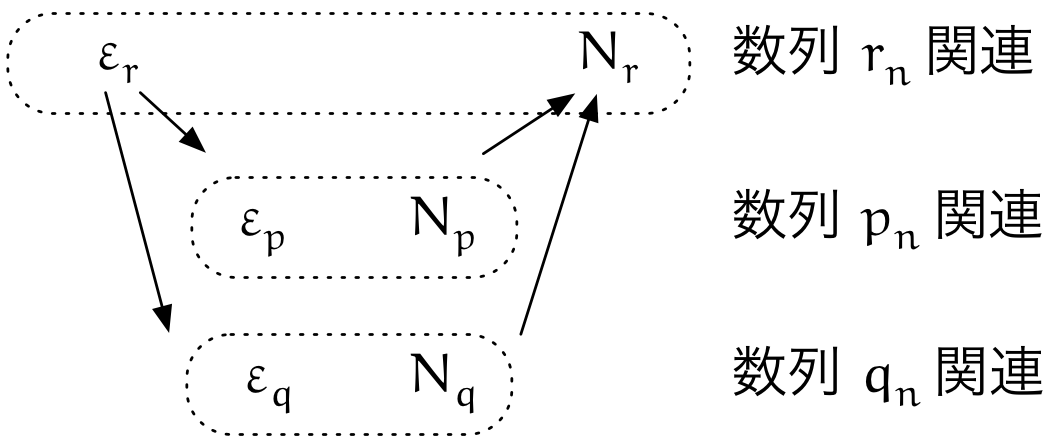
テトラ「《与えられているものは何か》と《求めるものは何か》を考えますと、 $\EPSLN_r$ が与えられたときに、 $\EPSLN_p$ と $\EPSLN_q$ を使って、 $N_p$ と $N_q$ を利用して、 $N_r$ を求める……という流れになるんじゃないかと思いました」
僕「へえ」
テトラ「なぜそう思ったかというと、 あたしの目的は $\EPSLN_r$ から $N_r$ を見つけることです。 でもあたしの使える武器というのは、 $p_n$ と $q_n$ の極限値が $0$ であるということだけです。 ということは言い換えると、 $\EPSLN_p,\EPSLN_q,N_p,N_q$ を使うしかないということですよね。 あたしの手の中にはそれしかないから、それを使うしかないです」
僕「そうそう! すごいなテトラちゃん。 そんなにはっきりと流れをとらえられるなんて、すごいよ!」
テトラ「き、恐縮です。 ところが、そこであたしの頭はストップしてしまいました。 文字が多くて頭の中を飛び回り始めたんです。 次の一歩がわからなくて」
僕「うんうん。文字だけを追うとそうなっちゃうかも。 ゆっくり段階を踏んで考えていこうよ。 まず、僕たちには挑戦者として $\EPSLN_r$ がやってきた」
テトラ「挑戦者?」
僕「つまり、 $\ABS{r_n} < \EPSLN_r$ という $n$ の条件を満たせるかという挑戦だね。 $\EPSLN_r$ が小さければ小さいほど厳しい条件になるから」
テトラ「ああ、そうですね。帯が狭くなりますから」
僕「僕たちは、十分大きな $n$ のすべてについて、 $\ABS{r_n} < \EPSLN_r$ の範囲に収めたい。 《十分大きな》というのはあいまいだから、 《$N_r$ という数が存在する》ことを明確にいいたい。 $n > N_r$ となるすべての $n$ について $\ABS{r_n} < \EPSLN_r$ を満たすような、 そのような $N_r$ は見つかるか?」
テトラ「はい、そこまではわかりますが……」
僕「$N_r$ が存在するということは、 最初の有限個の項は捨てられるということだね。 $n = 1, 2, 3, \ldots, N_r$ についての $r_n$ は無視できる。 捨てていい」
テトラ「はい、その感覚もわかります」
僕「ここで僕たちが使える $p_n$ と $q_n$ についても考えると、 $p_n$ も $q_n$ も最初の有限個の項を捨てさえすれば、 絶対値をいくらでも $0$ に近付けられるよね」
テトラ「はい、それもわかります」
僕「$r_n$ の定義は?」
テトラ「$r_n = p_n + q_n$ ですね。 $p_n$ と $q_n$ の両方を足したものが $r_n$ です。 具体的には、 $$ \begin{align*} r_1 &= p_1 + q_1 \\ r_2 &= p_2 + q_2 \\ r_3 &= p_3 + q_3 \\ &\,\vdots \\ \end{align*} $$ で……むむむ?」
僕「何か、ひらめいた?」
テトラ「ひらめいたわけではないのですが、 あたしたちが考えたいのは、 $$ \ABS{r_n} < \EPSLN_r $$ という不等式ですよね。 $r_n$ の定義からいえば、 $$ \ABS{p_n + q_n} < \EPSLN_r $$ を考えればいい……ってあたりまえのことでした」
僕「それ!それは大事だよね。だって、 $\ABS{p_n} < \EPSLN_p$ と $\ABS{q_n} < \EPSLN_q$ は使えるから」
テトラ「でも、 $\EPSLN_r$ と、 $\EPSLN_p, \EPSLN_q$ の関係が……わかりません」
僕「え? いやいや、その関係付けは僕たちがするんだよ。 不正確な言い方だけど、 $\EPSLN_p, \EPSLN_q$ は何でもいいんだから、 $\EPSLN_r$ をもとにしてうまく作ってあげればいいんだ」
テトラ「ははあ……もしかして、《半分こ》すればいいのでしょうか?」
僕「半分こ?」
テトラ「$\EPSLN_r$ を二人で《半分こ》するんです。つまり、こうです。 $$ \left\{\begin{array}{llll} \EPSLN_p &= \dfrac{\EPSLN_r}{2} \\ \EPSLN_q &= \dfrac{\EPSLN_r}{2} \\ \end{array}\right. $$ これで挑戦者 $\EPSLN_r$ を二人の数列で分担させられます! こうやってもいいということですよね? だって、 $\EPSLN_p, \EPSLN_q$ はどんな正の数でもいいわけですから」
僕「いいよ! どんどん進めて!」
テトラ「ええと、 $\EPSLN_p$ に対しては、 $n = 1,2,3,\ldots,N_p$ の $p_n$ を捨てちゃいます。 それから、 $\EPSLN_q$ に対しては、 $n = 1,2,3,\ldots,N_q$ の $q_n$ を捨てちゃいます。 捨てちゃいます……あ、だめですね」
僕「あれれ?」
テトラ「二つの $N_p$ と $N_q$ が出てきますが、あたしが作りたいのは $N_r$ なんです……」
僕「うわ……すごく惜しいんだけど、あと一つヒント言ったら答えになっちゃうよ。 テトラちゃん、最後の一歩は自分でゴールしたいよね?」
テトラ「もちろんですっ! あと一歩なんですね? 考えます。ここまで考えたことは……」
僕「……」
テトラ「それで《求めるものは何か》というと、十分大きな $N_r$ でしたから……ああ、 先輩、わかりました。あたりまえのことでした。 $N_p$ と $N_q$ のどちらか大きい方を $N_r$ にすればいいだけなんですね……」
僕「そう! どちらか大きい方というか、小さくない方というか、ともかく、 $$ N_r = \max(N_p, N_q) $$ にするんだね。 ところで、急にテンション下がったみたいだよ、《元気少女》のテトラちゃん」
テトラ「いえいえ、すぐに気づけなかったのにがっかりしたのです……」
僕「そんなことないよ。特に $\EPSLN_r$ を二つに分けたところは発見ポイントだよね!」
テトラ「そうですね! では、答えをまとめます!」
解答1(極限値の和)
(証明)
二つの数列 $\LL p_n \RR$ と $\LL q_n \RR$ は、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & p_n \to 0 \\ n \to \infty & \REMTEXT{で} & q_n \to 0 \\ \end{array} $$ なので、次のことがいえます。
(1)どんな正の数 $\EPSLN_p$ に対しても、正の整数 $N_p$ を選んで、 $n > N_p$ であるすべての整数 $n$ について、 $$ \ABS{p_n} < \EPSLN_p $$ を満たすようにできます。
(2)どんな正の数 $\EPSLN_q$ に対しても、正の整数 $N_q$ を選んで、 $n > N_q$ であるすべての整数 $n$ について、 $$ \ABS{q_n} < \EPSLN_q $$ を満たすようにできます。 (ここまでは、定義をなぞっただけです)
いま、正の数 $\EPSLN_r$ に対して、 $\EPSLN_p,\EPSLN_q$ の値を、 $$ \left\{\begin{array}{llll} \EPSLN_p &= \dfrac{\EPSLN_r}{2} \\ \EPSLN_q &= \dfrac{\EPSLN_r}{2} \\ \end{array}\right. $$ と決めます。(これは発見ポイントです!)
すると、
ここで、 $N_r = \max(N_p, N_q)$ と置きます。(これも発見ポイントです!)
そうすると、
ここで、 $n > N_r$ のときの $\ABS{r_n}$ を調べていきます。 $$ \begin{align*} \ABS{r_n} &= \ABS{p_n + q_n} \\ &< \EPSLN_p + \EPSLN_q \\ &= \frac{\EPSLN_r}{2} + \frac{\EPSLN_r}{2} \\ &= \EPSLN_r \\ \end{align*} $$ ですから、 $n > N_r$ であるすべての $n$ について、 $$ \ABS{r_n} < \EPSLN_r $$ がいえました!
これで、 $n \to \infty$ で $r_n \to 0$ がいえました。
(証明終わりです!)
僕「すばらしいね!」
テトラ「ありがとうございます」
僕「細かい話だけど、テトラちゃんの証明の中で、 $$ \ABS{p_n + q_n} < \EPSLN_p + \EPSLN_q $$ はどうして成り立つかいえる?」
テトラ「えっ……だって、 $\ABS{p_n} < \EPSLN_p$ と $\ABS{q_n} < \EPSLN_q$ ですから……ああ、 そうですね。あたし、さりげなく絶対値をわけちゃってますね」
僕「そうだね。もちろん結果としては正しいんだけど、 いわゆる三角不等式を飛ばしちゃったよね。 $\ABS{x + y} \LEQ \ABS{x} + \ABS{y}$ の不等号には $=$ が含まれてる」
$$ \ABS{p_n + q_n} \LEQ \ABS{p_n} + \ABS{q_n} < \EPSLN_p + \EPSLN_q $$テトラ「確かにそうですね……」
僕「でも、証明はよくわかるよ」
テトラ「なんだか、すごく $\EPSLN{}N$ 論法がわかったような気がします。 有限個の項を捨てちゃえばいいという感覚です」
僕「いまは収束する二つの数列の和の極限を考えたけど、同じように数列の差の極限や、積の極限や、商の極限も考えられるよ。 商のときはゼロ割りの注意がいるけど」
テトラ「なるほどです。収束する数列では、基本的な計算は極限値で考えられる……?」
僕「そういうことになるね。基本的な計算によるけど」
テトラ「たとえば、数列の平均でもそうでしょうか」
僕「ああ、もちろんそうだね。 $\frac{p_n + q_n}{2}$ のような数列を考えれば、それは実質的に和と同じだからね」
テトラ「……あらら?」
僕「何かおかしい?」
テトラ「いえ、二つの平均 $\frac{p_n + q_n}{2}$ というのはいいんですが、あたしは別のことを考えていたんです」
僕「別のこと」
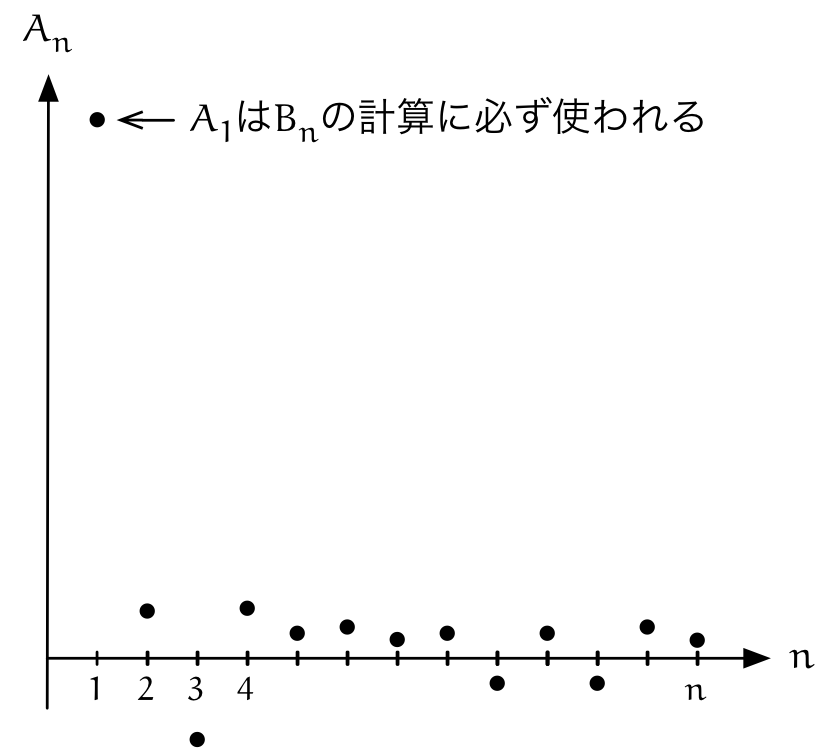
テトラ「二つの数列の平均ではなくて…… たとえば、 $n \to \infty$ で $A_n \to 0$ という数列 $\LL A_n \RR$ があったとしますよね。 そのとき、 $$ B_n = \frac{A_1 + A_2 + \cdots + A_n}{n} $$ という数列 $\LL B_n \RR$ を考えるんです」
僕「なるほど……《最初の $n$ 項の平均》ということだね」
$$ \begin{align*} B_1 &= \frac{A_1}{1} \\ B_2 &= \frac{A_1 + A_2}{2} \\ B_3 &= \frac{A_1 + A_2 + A_3}{3} \\ &\,\vdots \\ B_n &= \frac{A_1 + A_2 + \cdots + A_n}{n} \\ &\,\vdots \\ \end{align*} $$テトラ「はい。 $n \to \infty$ のとき、 $B_n \to 0$ になる……んでしょうか?」
僕「そりゃそうなるよね」
テトラ「ほんとうに、そうなんでしょうか……?」
僕「だってそうだよ。これは明らかだね」
テトラ「で、でも……もしかしたら $A_1$ がとても大きいかもしれませんよね。 ものすごく大きい $A_1$ があったとしても、 $A_n$ の極限を考えるときは《最初の有限個を捨てる》という必殺技が使えました」
僕「お……」
テトラ「でも、 $B_n$ はだめです。だって、 $$ B_n = \frac{A_1 + A_2 + \cdots + A_n}{n} $$ ですから、必ず $A_1$ が加味されてしまうからです。捨てられないんです。 $A_1$ は $5000$ 兆かもしれません。とてつもなく大きいかもしれません。 $B_n$ の収束を考えるとき、 どんな大きな $n$ に対しても、 $B_n$ を計算するときには、その大きな $A_1$ を使うことになってしまうんですが……」
僕「う……」
僕はテトラちゃんの鋭い指摘に言葉を失った。
確かにそうだな。 $A_n$ の収束は、有限個の $A_1,A_2,\ldots,A_N$ を捨てて考えることができた。 でも、《$A_n$ の最初の $n$ 項の平均》を数列にした $B_n$ には $A_1$ が必ず含まれてしまう。
直観的には $B_n$ は $0$ に収束すると思う。なぜなら、 $A_1$ がいくら大きいとしても、 平均を取るときには十分小さな $A_n$ たちがたくさん加算されて $n$ で割るわけだから。
だから、 $A_1$ の大きさは薄められてしまうはずだが……それは直観にすぎない。
確信するためには証明がいる。
テトラ「先輩?」
僕「ごめん、ちょっと考えさせて」
問題2(平均の極限)
数列 $\LL A_n \RR$ は、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & A_n \to 0 \\ \end{array} $$ とする。
ここで、数列 $\LL B_n \RR$ の一般項を、 $$ B_n = \frac{A_1 + A_2 + \cdots + A_n}{n} $$ で定義する。
このとき、 $$ \begin{array}{lll} n \to \infty & \REMTEXT{で} & B_n \to 0 \end{array} $$ といえるか。
いえるなら証明し、いえないなら反証せよ。

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 450本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2018年3月2日)